Page 1 :
WAVES, , CHAPTER-15, , WAVES, , Wave: A Wave is a sort of disturbance which transmits energy and momentum in a medium, without transfer of particle., Ex: Sound waves, light waves, waves of water, matter waves etc., Wave motion: The propagation of disturbance from one point to another point is called wave, motion., Types of waves:, (1) Based on Propagation, (i) Mechanical waves: Waves which requires a material medium for their propagation are called, mechanical waves., Ex: Seismic waves, Water waves, sound waves etc., Characteristics: 1) They cannot propagate in vacuum., 2) Particles in the medium will vibrate., 3) Depends on elastic properties of the medium., (ii) Electromagnetic waves: Waves which do not require a material medium for their propagation, are called mechanical waves., Ex: Light waves, X-rays, micro waves etc., Characteristics: 1) They can travel in vacuum, 2) Speed of the wave is 299792458 m/s, 3) Electric and magnetic field will oscilate, (iii) Matter waves: Waves associated with moving material particles are called matter waves., Louis de Broglie theoretically suggested that a moving matter such as electron, proton, neutron,, atoms or molecules is associated with matter waves., (2) Based on Vibration of particles of the medium., (i) Transverse waves: If the oscillations/vibrations in the medium are perpendicular to the, direction of wave propagation, then the waves are called transverse waves., Ex: Light waves, Seismic S-waves etc., Characteristics:, 1) They contain alternate crests and troughs., 2) Crests are the elevations formed in the medium and troughs are the depression formed in a, medium., 3) Transverse waves are either mechanical or electromagnetic., 4) They can travel only in solids, if waves are mechanical., (ii) Longitudinal waves: If the oscillations/vibrations in the medium are along or parallel to the, direction of wave propagation, then the waves are called transverse waves., Ex: Sound waves, pressure waves, Seismic P-waves etc., , Karnataka PUC Physics Telegram channel, , Page|1

Page 2 :
WAVES, , Characteristics:, 1) They contain alternate compressions and rarefactions., 2) Compressions are the portion of the medium having more density and rarefactions are the, portions of the medium having less density., 3) They are always mechanical., 4) They can travel in solids, liquids and gases., Terms related to waves., Amplitude: The maximum displacement of a particle of the medium from its equilibrium position., Time period: Time taken by the particle to complete one oscillation. or It is the time in which one, wave is set up in a medium., Frequency: It is the number of waves setup in a medium in one second., , Frequency is expressed in hertz (Hz) and 1 hertz=1 cycle per second., Wave length: The distance between two consecutive particles which are in same phase., Wave length is denoted by (lambda) and expressed in metre., Progressive wave: A wave which travels from one point to another point of the medium in the, same direction without change in its amplitude is known as a progressive wave., Progressive wave equation: An equation that gives the displacement of a particle in a medium at, any point, at any instant of time is called a progressive wave equation., A sinusoidal wave is represented by the equation, ( ), (, ), ( ) Displacement of the particle, Amplitude of the wave, Angular wave number or propagation constant, angular frequency of wave, initial phase angle, Phase: The quantity (, At, and, ,(, , ) is called phase of the wave., ), is called initial phase angle., , Angular wave number: It is the change in phase with respect to distance., It is given by, , ⁄ and expressed in rad/metre., , Angular frequency: It is given by, , ⁄ and expressed in rad/second., , Speed of a travelling wave: Speed of a wave is given by,, , or, , ⁄, , Note: When a wave enters from one medium to another, both speed and wavelength change but, the frequency remain unchanged., Speed of a transverse wave on stretched string: It is given by,, Where, , Tension in the string and, , Karnataka PUC Physics Telegram channel, , √ ⁄, , mass per unit length of the string., Page|2

Page 3 :
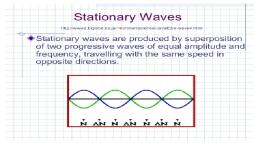
WAVES, , Speed of sound – Longitudinal wave: It is given by,, Where, , Modulus of elasticity and, , (i) In solids,, , (, , (ii) In fluids,, , (, , √ ⁄, , density of the medium, , ) then, ) then, , √ ⁄, √ ⁄, , Newton’s formula for speed of sound in gas: Newton suggested that,, (i) During compression, temperature of the medium increases and heat is lost to the surrounding., (ii) During rarefaction, temperature is absorbed from the surrounding., Thus the conditions are, isothermal but there is a change in pressure and volume of the air., (, , )(, , ), Since, , ⁄ ), , (, But,, , √ ⁄ in air. Then,, , √ ⁄, , According to this formula, at STP,, Hence, Newton’s formula needs correction., Laplace correction: Laplace suggested that,, (i) Vibrations of the layers of air are so rapid and no time for heat transfer between the layers., (ii) Air is a bad conductor of heat., Thus, the condition is Adiabatic but not isothermal., where, ratio of specific heat, ), Differentiate, (, , (, √, , ⁄ ), , ⁄, , According to this formula, at STP,, value, , This Formula is called Newton’s-Laplace formula., a good agreement with practical, , Reflection of waves: When a wave travelling in a medium, meets a rigid boundary, it gets, returned to the same medium is called reflection of wave., The reflected wave has same shape as the incident wave, but it suffers a phase change of, , or, , Standing waves or Stationary wave: When two waves of equal amplitude and wavelength, travelling along a line in opposite direction and superimpose the resulting wave pattern is called a, stationary wave of standing wave., Ex: (i) Stationary waves produced in the closed and open pipe., (ii) Stationary waves produced in the vibrating string., Karnataka PUC Physics Telegram channel, , Page|3

Page 4 :
WAVES, , Nodes: At some positions in the wave, the amplitude of the particles are zero, these points are, called Nodes., Antinodes: At some points in a wave, the amplitude of the particles are maximum or the particles, vibrate with maximum amplitude, these points are called antinodes., Conditions for Nodes and antinodes:, ( ), ( ), , (, , ), , Hence, (i) The distance between two consecutive node or antinode is ⁄, (ii) The distance between a node and the antinode is ⁄, Normal Modes: In a stationary wave, the possible frequencies of oscillation of the system is, characterised by set of natural frequencies called Normal modes., Modes of vibration in a closed pipe: A closed pipe is one in which one end is closed and other is, opened. Inside a closed pipe,, (i) Open end always has an antinode, because open end have maximum freedom to vibrate., (ii) Closed end always has a node, because closed end are not free., (iii) Frequency of vibration of air column depends on (a) length of pipe and (b) mode of vibration., , First mode of vibration: If the air column consists of single node and a single antinode, the mode, of vibration is called first mode of vibration or Fundamental mode., If, is the wavelength and, is the length of the pipe, then, , is called fundamental frequency and this is the minimum frequency., Second mode of vibration: In second mode of vibration two modes and two antinodes are formed., If, is the wavelength and, is the length of the pipe, then, Karnataka PUC Physics Telegram channel, , Page|4

Page 5 :
WAVES, , (, , ), , Third mode of vibration: In this type of vibration three nodes and three antinodes are formed., If, is the wavelength and, is the length of the pipe, then, , (, Now,, , ), , , hence Only odd harmonics are present., , Modes of vibration in Open pipe: A pipe opened at both ends is called open pipe. In open pipe, antinodes are always formed at the open ends., , First mode of vibration: If the air column vibrate such that the entire air column consists of a, single node and two antinodes, the mode of vibration is called first mode of vibration of, fundamental mode., If, is the wavelength and, is the length of the pipe, then, , is called fundamental frequency and this is the minimum frequency., Second mode of vibration: This mode of vibration consists of two nodes and three antinodes., If, is the wavelength and, is the length of the pipe, then, (, , ), , Third mode of vibration: This mode of vibration consists of three nodes and four antinodes., If, is the wavelength and, is the length of the pipe, then, , (, Now,, , ), , , hence both even and odd harmonics are present., , Standing waves in stretched string: In a stretched string node are always formed at the fixed ends., , Karnataka PUC Physics Telegram channel, , Page|5

Page 6 :
WAVES, , First mode of vibration: Two nodes and a single antinode are formed., If, is the wavelength and, is the length of the pipe, then, , is called fundamental frequency and this is the minimum frequency., Second mode of vibration: This mode of vibration consists of, three nodes and two antinodes., If, is the wavelength and, is the length of the pipe, then, (, , ), , Third mode of vibration: This mode of vibration consists of four nodes and three antinodes., If, is the wavelength and, is the length of the pipe, then, , (, Now,, , ), , , hence both even and odd harmonics are present., , Laws of vibration in a stretched string:, Speed of transverse wave is given by,, (), , √ ⁄, , √ ⁄, , ( ), , (, , ), , √ ⁄, , ( ), , (, , ), , √ ⁄, , √ ⁄, (1) Law of length: Frequency of vibrating string is inversely proportional to length of the string., , (2) Law of tension: Frequency of vibrating string is directly proportional to square root of the, tension in the string., √, (3) Law of mass: Frequency of vibrating string is inversely proportional to square root of the mass, per unit length of the string., √, , Karnataka PUC Physics Telegram channel, , Page|6

Page 7 :
WAVES, , Doppler Effect: The apparent change in the frequency of source due to relative motion between, the source and the observer is called Doppler Effect., Applications of Doppler Effect:, 1) It is used to determine the velocities of aeroplanes and submarines., 2) Used to measure speed of automobile., 3) Doppler Effect in light is used to determine the velocities of celestial bodies., Expression for Apparent frequency:, (i) Source moving and observer stationary., Consider a source S moving with a velocity, Time period of wave is and velocity is ., At time, , the distance between the source and the, observer is ., At position, source emits a wave., Time taken by the wave to reach the observer is, , ⁄, , Now the source moves to new position, at time, At position, source emits another wave, Time taken by the wave to reach the observer is, , ( ⁄ ), , *, , +, , Time period of the wave as recorded by observer is,, ( ⁄ ), (, , [, , ], , ( ⁄ ), , ), (, , ), , (, , ), , (ii) If Source moving towards the observer, then, (, , ), , Karnataka PUC Physics Telegram channel, , Page|7

Page 8 :
WAVES, , Suggested questions., One mark., 1) Define the amplitude of a wave., 2) State the principle superposition of waves., 3) What are standing waves?, 4) When the beats are formed?, 5) Mention any one application of beats., Two marks., 1) Discuss the types of waves based on vibration of the particles in a medium., 2) A wave travelling in a medium having the frequency, . and wave length of, the velocity of the wave?, 3) What are nodes and antinodes?, 4) What harmonics are present in (a) an open pipe (b) a closed pipe?, 5) What is Doppler Effect? Mention its application., , . Find, , Three marks., 1) Define the terms (i) Wave amplitude, (ii) Wave period, (iii) Wave frequency., 2) Discuss the types of waves based on the wave propagation in a medium., 3) Give the Newton’s formula for the speed of sound in air and hence explain the Laplace’s, correction., 4) Discus the modes of vibrations in closed pipe., 5) Discus the modes of vibrations in open pipe., 6) State the Laws of vibration in a stretched string., Five marks., 1) Give any five differences between progressive waves and stationary waves?, 2) What are stationary waves? Show that the frequency of vibration of stretched string contains, all harmonics., 3) Derive the expression for beat frequency., Numerical Problems., 1) A train standing at the outer signal of a railway station blows a whistle of frequency, in, still air. What is the frequency of the whistle for a platform observer when the train (a), approaches the platform with a speed of, (b) Recedes from the platform with the, speed of, (c) What is the speed of sound in each case? (The speed of the sound in still, air, ), 2) A train is moving with a speed of, , blowing a whistle of frequency, in still air., What is the frequency of the whistle as heard by a stationary observer on a platform when (i), train approaches and (ii) recedes from the observer? (Speed of the sound in still air, ), 3) The equation of a sinusoidal wave travelling along negative x-axis is, (, ), where and are in metres and is in seconds. Calculate the amplitude, wave length,, frequency and wave velocity., ( ), 4) A wave travelling along a string is given by, (, ) where SI, units are used. Calculate: (a) The amplitude (b) The wavelength (c) The period (d) The, frequency., Karnataka PUC Physics Telegram channel, , Page|8

Page 9 :
WAVES, , 5) A string of mass, is under a tension of, . The length of a stretched string is, . If, transverse jerk is struck at one end of the string, how long does the disturbance take to reach, the other end?, 6) A policeman blows a whistle of frequency, , as a car speeds fast him with a velocity of, Find the change in frequency as heard by the driver of the car, just as he passes the, policeman. (Velocity of sound is, ), 7) When a simple harmonic wave is propagated through a medium, the displacement of a, particle (in metre) at any instant of time is given by, , *, , + with lengths, , expressed in metre and time in second. Calculate the wavelength, amplitude, frequency and, velocity of the wave., 8) The apparent frequency of a note when listener moves towards a stationary source with, velocity, is, . When he moves away from the same source with same speed the, apparent frequency of note is, . Calculate velocity of sound in air., 9) A train is moving at speed of, towards a station, is sounding a whistle of frequency, . What are the apparent frequencies of the whistle as heard by a man on the plot form, when the train a) approaches him b)recedes from him?(speed of sound in air, ), , Karnataka PUC Physics Telegram channel, , Page|9