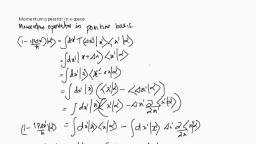Page 1 :
Ehrenfest’s Theorem, Let’s explore some of the consequences of our result:, d, i, Q =, h, dt, , ), ) ), ∂Q, H ,Q +, ∂t, , [, , ], , For instance, let’s look at the time dependence of the expectation value of the position:, i, d, x =, h, dt, , ), ) ), ∂x, H,x +, ∂t, , [, , ], , Now, the x operator doesn’t depend explicitly on time, so the second term is zero, and the, Hamiltonian operator is:, , ), ), p2, + V ( x) ⇒, H =, 2m, ), ⎞ )⎤, i ⎡⎛ p 2, d, + V ( x ) ⎟⎟, x ⎥, x =, ⎢⎜⎜, h ⎣⎝ 2m, dt, ⎠ ⎦, but ,, V ( x) = f ( x), so, [V ( x ) , x) ] = 0 ⇒, ), i, i ⎡ p 2 )⎤, d, [ p) 2 , x) ], , x⎥ =, x =, ⎢, 2mh, dt, h ⎣ 2m ⎦, i, ) ) ), ) ) ), p[ p , x ] + [ p, x ] p, =, 2mh, −i ), ), pih + ihp, =, 2mh, 2h ), p, =, 2mh, ), p, =, m, You should recognize this as the velocity is equal to the momentum divided by the mass., What about the time rate of change of the expectation value of the momentum?
Page 2 :
), ), p2, + V ( x) ⇒, H =, 2m, ), ⎞ )⎤, d, i ⎡⎛ p 2, + V ( x ) ⎟⎟, p ⎥, p =, ⎢⎜⎜, dt, h ⎣⎝ 2m, ⎠ ⎦, but ,, ), ⎡ p2 )⎤, ⎢ 2m , p ⎥ = 0 ⇒, ⎣, ⎦, d, i, [V ( x ) , p) ], p =, dt, h, and we must explore this commutator:, , [V ( x ) , p) ], , ), ), = Ψ VpΨ − Ψ pVΨ, h ∂Ψ, h ∂, (VΨ ), − Ψ, i ∂x, i ∂x, h ∂Ψ, h ∂V, h ∂Ψ, = Ψ V, − Ψ, Ψ − Ψ V, i ∂x, i ∂x, i ∂x, h ∂V, = − Ψ, Ψ, i ∂x, = Ψ V, , so that we now have:, ∂V, −i, h ∂V, d, Ψ, Ψ = −, p =, h, dt, i ∂x, ∂x, , Recognize this? F = ma = dp/dt = -dV/dx, This reduction of quantum mechanical dynamics to the classical trajectories is known as, Ehrenfest’s Theorem. It only holds for expectation values (averages of the, measurements) and not for the eigenvalues themselves., The difference between quantum and classical trajectories is a result of the finite special, extent of the wave packet, and thus that the derivative of V with respect to x is taken at, different points. These parts of the packet then “feel” a different force, and the, trajectories interfere.