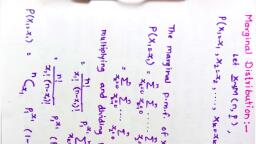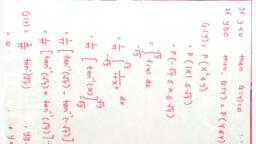Page 1 :
Scanned with CamScanner, Multinomial Distribution:-, Multinomial dist" is a generaliza-, tion of Binomial dist? 1f the outcomes of, P(X, x, , X2=2,... ,X= Xx) =, n!, Pi, ..., X: (0, 1, 2,. .. n) st Zi, trial are only 2 then we use Binomia!, dist. 1F the outcomes of the trial aYe, 3 then we use trinomial dist! If Hthe, outcomes of the triels are more than 3, ...., O<Pi <!, sit. Eri el, > Ow., then we use multinomial dist?, Thus, in case of multinomial dist? Note : In multinomial dist", dt assume that there are 'k' mutual parameters are (n, P) but since, exclusive and exhaustive outcomes of a, E Pizl it is to be noted that their, are k parameters in multinomial dist, Notation:- It is dended by,, trial ģ there are, 'n' independent, trials., Def ? A discrete rv. X = (X,,X... ,X), X→ M(n, P), is said to fellow multinomial dist?with, parameter (n, P) (f = R,B,. -. , P), if its p.m.f. is given by,, OY, (X1, X2, -.-. Xx) -M(n, P, R,--e)

Page 2 :
Scanned with CamScanner, : On the basis of survey conducted by a PCNO. of persons prefering Ni, N2,, research company it was found that, respective market shares of 4 newspapers, ie. N, , N2, N3, Ny are 15%., 20%, 30%.,, 35%, and investigatur independently, interviewed · 15 persons on their, N3, Ng are 3,2,4,6 respecttively), =P(x,=3,X2=2,X3=4, Xq =6), 15!, x (0-15) Co-25 co-3)" co-35), 3! 2! 4! 6!, newspape r preferences. Find the, poobab i lity that no. of persons, prefering Ni Ne, Ng & Ny are, 3, 2,486 respectively., O. 01267, le can easily verify that,, Sol";- Let xis no. of persons prefering £ I P(X,-2, X%,.Xx÷Xx)., ....., news paper, Ni, sie1,2..4, a person prefering, Piz, Probability of, newspaper Ni, ...., is1,2.4, 4 also glven that,, Piz o-15, P2 = 0. 2 , Pg=0'3, Py= 0:35, he 15