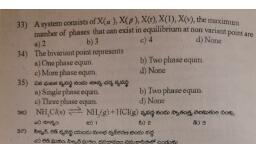Page 2 :
THE PHASE RULE, , “phase rule predicts itati > equilibri oe, [Phase re predicts quantitatively the equilibrium existing between different phases of a heterogencous systems.”” |, , ; PHASE RULE, , _ The phase rule is a generalisation given by Willard Gibbs (1874), which seeks to explain the, equilibria existing in heterogeneous systems. It may be stated as : “provided the equilirbium between, any number of phases is not influenced by gravity, or electrical, or magnetic forces, or by surface action and, only by temperature, pressure and concentration, then the number of degrees of. freedom (F) of the system is, related to the number of components (C) and of phases (P) by the phase rule equation, ., , F=C-P+2, , for any systent at equilibrium at a definite temperature and pressure.” This rule, if properly applied, has, no exception., , Explanation of terms : (1) Phase : A phase is defined as “‘an homogeneous, physically distinct, and mechanically separable portion of system, which is separated from other such parts of the systent by, definte boundary surfaces”. For example :, , (i) At freezing point, water consists of three phases :, . x, , Ice (s) <> Water(!) == Water vapour (g), , , , (ii) A gaseous mixture, being thoroughly miscible in all proportions, will constitute one phase, only. Thus, a mixture of N; and H, forms one phase only., , (iii) If tivo liquids are immiscible (i.e., benzene and water), they will form two separate phases., (iv) If two liquids are miscible (i.e., alcohol and water), they will form one liquid phase only., , (v) A solution of a substance in a solvent consists of one phase only, e.g., glucose solution in, water., , (vi) Each solid makes up 4 separate phase, except in the case of solid solutions, e.g., many forms, of a sulphur can exist together, but these are all separate phases., , (vii) A heterogeneous mixture like:, CaCOx(s) = CaOls)+ CO.), , consists of three phase (i.e., two solids and one gaseous)., Similarly, in the equilibrium reaction,, Fe(s)+H,O(g) = FeO) + Hg), there are two solid phases, Fe and FeO and one gaseous phase consisting of H,O(g) and H,{g). Thus,, three phases exists in equilibrium., , , , _ 8a an awa of tho fanndars, , Scanned with CamScanner
Page 3 :
ENGINEERING CHEMIstpy, 392, , i i . Thus, Mohr’s salt [Fes, (NH,),SO,.6H,0] solution constitutes a single phase, althoug, H,0. b indevende: ;, ‘ ” 05 er of independent Variable, t is meant “the smallest num er, (2) Component : By the term componen ‘ ° ition of each phase can, constituents, taking part in the state of equilibrium, by means of which the compos’ of P N be, expressed in the form of chemical equation’. For example :, (i) Tn the water system,, Ice (s)_ = Water (!) = Vapour (g), i it i: nent systent,, the chemical composition of all the three phases is H,O. Hence, it is one a e n _, i intic, liquti our, the chemica, (i) The sulphur system consists of four phases, rhombic, monoclinic, liquid and vap ‘mical, , . composition of all phases is S. Hence, it is one component systent., , (ii) In the dissociation of NH,Cl in a closed vessel,, NH,Cl(s) = NH,Cl@) = NH,(g)+HCI), the proportions of NH; and HCl are equivalent and hence, the composition of both phases (solid, , and gaseous) can be expressed in terms of NH4C1 alone. Hence, the number of component is one,, However, if NH; or HCl is in excess, the system becomes a two component system., , (iv) A system of saturated solution of NaCI consists of solid salt, salt solution and water vapour., , The chemical composition of all the three phases can be expressed in terms of NaCl and H,0., Hence, it is a two component system,, , (v) In the thermal decomposition of CaCO,,, CaCOys) = CaO(s) + CO,(g), , the composition of each of the three phases can be expressed in terms of at least any two of the, independently variable constituents, CaCO, CaO and CO). Suppose CaCO, and CaO are chosen, as the two components, then the composition of different phases is represented as follows :, , Phase : CaCO, = CaCO; +0CaO, , Phase: CaQ=0 CaCO, + CaO, , Phase: - CO,= CaCO, = CaO, , Thus, it a two coniponent systent., , (vi) In the dissociation reaction,, , CuSO,.5 H,O(s), , the composition of each phase can be Tep, Hence, it is tivo component system., , (vii) In the equilibrium, Fe(s) + H,0 (g), required to express the composition of each ph, , Number of components of a system ma, , constituents of the system minus the number of e, state. For example :, , T= CuSO,.3 H,0(s) +2 H,0(g), , resented by the simplest components, CuSO, and H,0., , = FeO(s) + Ha(g), the minimum components, ase is three, Evidently, it is a three component systent., y alternatively be defined as the number of chemical, quations relating to these Constituents in an equilibrium, (1) Dissociation of KCIO, in a closed vessel : Following, 2 KCIO, (s) = 2ka (s)+3 ©) (g), , No. of constituents = 3, , Scanned with CamScanner
Page 4 :
THE PHASE RULE, 393, , . _{KCIPIOF |, , Now ae 4, "= TKeloge = Ol (1), , [. Active mass of a solid is, . ; ; $8 § is taken constant], ». No. of equations relating the concentration of constituents = 1., , con a of components =3-1=2 i.¢., it is a ftvo component system., (2) Dissociation of NH,CI: (1) Only NH,C1 is heated ina closed vessel. The equilibrium existing, , NH,Cl(s) =3 NH;(g)+ HCl (g), , (NH,] = [HCl] li), _ [NH,I[HCl], Also Ka ="TH,cy) = NESIHCH ii), , because the active mass of NH,Cl (s) is constant., , Now number of components, C, =No. of constituents — [No. of equations relating to concentration of constituents], =3(NH,Cl, NH; and HCl)-2=1, ie., it is a single component system., (ii) When NH,Cl is heated in a closed vessel alongwith NH3 or HCI. At equilibrium :, Keg = (NH][HCl] (i), But [NH,] # [HCI] ---(ii), Only one equation (i) relates the concentrations of constituents, No. of component, (C) =3-1=2, ie., under the above conditions, the system has fvo, components., (3) Degree of freedom or variance : By the term “degree of freedom is meant by” the minimum, , number of independently variable factors, such as temperature, pressure and contposition of the phases, which, must be arbitrarily specified in order to represent prefectly the condition of a system’. For example :, , (i) In case of water system, Ice (s) = Water (I) = Vapour (g), if all the tree phases are, present in equilibrium, then no condition need to be specified, as the three phases can be in, , equilibrium only at particular temperature and pressure. The system is, therefore, zero variant or, non-variant or invariant or has no degree of freedom. If condition (c.g., temperature or pressure) is, , altered, three phases will not remain in equilibrium and one of the phases disappears., (ii) For a system consisting of water in contact with its vapour,, Water (/) == Water vapour (9),, , we must state either the temperature or pressure to define it completely. Hence, degree of freedom is, , one or system is univariant., , (iii) For a.system consisting of water vapot, temperature and pressure in order to describe the, or has two degrees of freedom., , (iv) For a system consisting of,, NaCl (s) <2 NaClwater (aq) = Water vapour (9),, , because the saturation solubility is fixed ata, , r phase only, We must state the values of both the, system completely. Hence, the system is bivariant, , we must state eifier the temperature or pressure,, particular temperature or pressure. Hence, the system is univariant., , Scanned with CamScanner
Page 5 :
— ig, , 394 ENGINEERING CHEMISTRY, , (@) Fora gaseous mixture of Ny and H,, we must state both the pressure and temperaure, because, , if pressure and temperature are fixed, the volume automatically becomes definite. Hence,, gaseous system, two factors must be sta, , degrees of freedom (or bivariant system)., , for a, ted in order to define it completely and thus, it has tvo, , Merits of phase rule : (1) It is applicable to both physical and chemical equilibria. (2) It requires no, , information regarding molecular/micro-struture, since it is applicable to macroscopic systems. (3) It is a, convenient method of classifying equilibrium states in terms of phases, components and degrees of freedom,, (4) It helps us to predict the behaviour of a system, under different sets of variables. (5) It indicates that, different systems with same degree of freedom bebave similarly. (6) It does not take into cognizance of either, the nature or quantities of component present in the system. (7) It helps in deciding whether under a given, set of conditions : (a) various substances would exist together in equilibrium or (b) some of the substances, present would be interconverted or (c) some of the substances preserit would be eliminated., , Limitations of phase rule: (1) It can be a, , pplied only for system in equilibrium. Consequently, it is of, little value in case of very slow equilibrium state, , attaining system. (2) It applies only to a single equilibrium, system ; and provides no information regarding any other possible equilibria in the system. (3) It requires, , utmost care in deciding the number of phases existing in an equilibrium state, since it considers only the, number of phases, rather than their amounts. Thus, even if a trace of the phase is present, it accounts towards, , the total number of phases. (4) It conditions that all phases of the system must be present simultaneously,, under the indentical conditions of temperature and pressure. (5) It conditions that solid and liquid phases, must not be in finely-divided state ; otherwise deviations occurs., , Scanned with CamScanner