Page 2 :
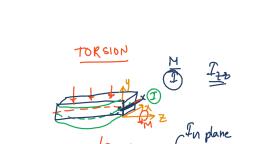
torsion in Solid and Hollow Circullar Shafts 28, 3.4 _PuRE Torsion, , Amember is said to be under pure torsion when it is subjected to a torque only, withou!, being associated with any bending moment or axial force., , assumptions for a circular shaft subjected to Torsion, , Following assumptions are made, while finding out shear stress in a circular shaft, subjected to torsion., , (i) The material of the shaft is uniform throughout., , (ii) The twist along the shaft is uniform., , (iii) Normal cross sections of the shaft, which were plane and circular before the twist,, remain plane and circular even after the twist., , (iv) All diameters of the normal cross-section, which were straight before the twist,, remain straight after the twist., 8.4.1 Torsion Equation, Let, T = Maximum twisting moment or torque, D = Diamter of the shaft., Jorl, = Polar moment of inertia., + = Shear stress., C= Modulus of rigidity., @ = The angle of twist (radians)., ¢ = Length of the shaft., The fig. show a shaft fixed at one end and torque being applied at the other end. Ifa line, LM is drawn on the shaft, it will be distored to LM’ on the application of the torque; thus, corss-section will be twisted through angle 6 and surface by angle 4., , , , MM’, Here, shear strain, ¢=—— Also, > =o, , Scanned with CamScanner
Page 4 :
yr, , forsion in Solid and Hollow Cireullar Shafts, —, Thus, T= txZ where , z02, , , , , For a shaft of given material, the maximum permissible shear stress 1 fixed a, the greatest twisting moment that the shaft can withstand is propertional to the, modulus of the shaft. Polar modulus of the secton is thus measure of strength of a4 :, in torsion. a, 8.5 Ho tow Circutar SHArr, , Torsion equation equally holds good, for hotlow shafts and can be, established in the same way., Consider a hollow circular shaft, subject to a torque T., , Let R = Outer radius of the shaft., r= Inner radius of the shaft., , 1 = shear stress at radius R,, , Let, dT = Turning moment on the elementary ring,, , = 1, .20X.dx.X, , ' ;, . 2mx.dX.K test ont, «mm, Integrating both sides, we Bet Jar fr . Boe em, , , , afh, Wh. omedux =o fx! =2n le 22 Eats, ote fav-fpanaxe z Jatt or Thal 2 aA, wo Hebe pe, 16 D, , , , or, , Scanned with CamScanner
Page 5 :
es, , , , , , , , , , , , ™ . Mechanics of Solids, , , , 8.6 ‘TorsionaL RiGipiry, , ‘ . T C Te, From the relation 7 = ° ; We have 0= a, , Since C, ¢ and Jare constant fora given shaft, 0 the angle of twist is directly propertional, , to the twisting moment. The quantity < is known as torsional rigidity and is represented, by K., CT, , From the above relation, we have K = FG, , 8.7 Power Transmitren By tHe SHAFT, Let a force F newton acting tangentially on the shaft at a radius of R. If the shaft due, to this turning moment (F x R ) starts rotating at N rpm then,, , Work supplied to the shaft / sec,, =Fx distance moved / sec., = Fx2nRN/60 Nm/s, , , , or Power, pa Ex2mRN A ts, 6, or pa lX2mN py (-. T =FxR), 60x 1000, , where, T is the mean / average torque is Nm, , 8.8 ImportTANCE OF ANGLE OF TWiST AND VARIOUS STRESSES IN SHAFT, Angle of Twist, , In many problems such as torsion of shafts of milling machines and drilling machines,, the angle of twist 0 is required to be restricted. In many applicational vibration problems,, the angle of twist is also needed. Because shafts fail beyond their limiting values., , 8.9 Stresses in SHAFTS, , Ina shaft the following significant stresses occurs :, (i) Maximum shear stress occurs on the cross - section of the shaft at its outermost surface., , (i) Themaximum longitudinal shear stress occurs at the surface of the shaft on the longitudinal, planes passing through the longitudinal axis of the shaft., , Scanned with CamScanner