Page 1 :
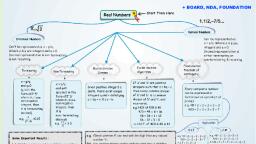
CBSE Class 10 Mathematics, Important Questions, Chapter 2, Polynomails, , 1 Marks Questions, 1. The graphs of y=p(x) are given to us, for some polynomials p(x). Find the number of, zeroes of p(x), in each case., , (i), , (ii), , (iii), , 1
Page 2 :
(iv), , (v), , (vi), , Ans. (i) The graph does not meets x-axis at all. Hence, it does not have any zero., (ii) Graph meets x-axis 1 time. It means this polynomial has 1 zero., (iii) Graph meets x-axis 3 times. Therefore, it has 3 zeroes., (iv) Graph meets x-axis 2 times. Therefore, it has 2 zeroes., , 2
Page 3 :
(v) Graph meets x-axis 4 times. It means it has 4 zeroes., (vi) Graph meets x-axis 3 times. It means it has 3 zeroes, , 2. Which of the following is polynomial?, (a), , (b), , (c), , (d) none of these, Ans. (d) none of these, , 3. Polynomial, , is a, , (a) linear polynomial, (b) quadratic polynomial, (c) cubic polynomial, (d) bi-quadratic polynomial, , Ans. (d) bi-quadratic polynomial, , 4. If, , and, , are zeros of, , , then the value of, , is, , (a) 5, (b) -5, (c) 8, (d) -8, , 3
Page 4 :
Ans. (b) -5, , 5. The sum and product of the zeros of a quadratic polynomial are 2 and -15, respectively. The quadratic polynomial is, (a), (b), (c), (d), Ans. (b), , 6. If p (x) = 2x2 – 3x + 5, 3x + 5, then P(-1) is equal to, (a) 7, (b) 8, (c) 9, (d) 10, Ans. (d) 10, , 7. Zeros of p (x) = x2 – 2x - 3 are, (a) 3 and 1, (b) 3 and -1, (c) -3 and -1, (d) 1 and -3, Ans. (b) 3 and -1, , 4
Page 5 :
8. If, , and, , are the zeros of 2x2 + 5x - 10 , then the value of, , is, , (a), , (b) 5, (c) -5, (d), , Ans. (c)-5, , 9. A quadratic polynomial, the sum and product of whose zeros are 0 and, , respectively is, (a) x2+, , (b) x2 -, , (c) x2 – 5, (d) None of these, Ans. a) x2+, , 10. Which of the following is polynomial?, (a), , (b), , (c), , 5
Page 6 :
(d) none of these, Ans. (d) none of these, , 11. Polynomial, , is a, , (a) linear polynomial, (b) quadratic polynomial, (c) cubic polynomial, (d) bi-quadratic polynomial, Ans. (d) bi-quadratic polynomial, , 12. If, , and, , are zeros of, , , then the value of, , is, , (a) 5, (b) -5, (c) 8, (d) -8, Ans. (b) -5, , 13. The sum and product of the zeros of a quadratic polynomial are 2 and -15, respectively. The quadratic polynomial is, (a), (b), (c), (d), Ans. (b), , 6
Page 7 :
CBSE Class 10 Mathematics, Important Questions, Chapter 2, Polynomails, , 2 Marks Questions, 1. Find the quadratic polynomial where sum and product of the zeros are a and, , ., , Ans. Polynomial, , 2. If, , are the zeros of the quadratic polynomial, , and, , value of, , find the, , +, , Ans., , 7
Page 8 :
3. If the square of the difference of the zeros of the quadratic polynomial f(x) = x2+ px, +45 is equal to 144, find the value of p., , Ans., , 4. Divide, , by, , Ans., , 5. Find the value of ‘k’ such that the quadratic polynomial x2 - (k + 6) x + 2 (2k +1) has, sum of the zeros is half of their product., , 8
Page 9 :
Ans. Sum of the zeros =, , 6. If, , that (, , and, , +1) (, , are the zeros of the quadratic polynomial f(x) = x2 – p (x + 1) – c, show, , +1) = 1 – c., , Ans., , 7. If the sum of the zeros of the quadratic polynomial f (t) = kt2 + 2t + 3k is equal to their, product, find the value of ‘k’., Ans., , 9
Page 10 :
8. Divide (x4 - 5x + 6) by (2 – x2)., Ans., , Quotient =, , Remainder = -5x + 10, , 9. Find the zeros of the polynomial p(x) = 4, , x2 + 5x – 2, , and verify the relationship, , between the zeros and its coefficients., Ans., , 10
Page 11 :
10. Find the value of ‘k’ so that the zeros of the quadratic polynomial 3x2 – kx + 14 are in, the ratio 7:6., Ans. Let the zeros are 7p and 6p., , 11. If one zero of the quadratic polynomial f(x) = 4x2 – 8kx – 9 is negative of the other,, find the value of ‘k’., Ans., , 11
Page 13 :
CBSE Class 10 Mathematics, Important Questions, Chapter 2, Polynomails, , 3 Marks Questions, 1. Apply division algorithm to find the quotient q (x) and remainder r (x) an dividing f, (x) by g (x), where, Ans., , 2. If two zeros of the polynomial, , are, , , find the, , other zeros., Ans. Two zeros are, , 13
Page 14 :
Now,, , 3. What must be subtracted from the polynomial, that the resulting polynomial is exactly divisible by, , so, ?, , Ans., , We must be subtract (2x – 3) to become a factor., , 14
Page 15 :
4. What must be added to, divisible by, , so that it may be exactly, , ?, , Ans., , So we must be added, , 5. Find all the zeros of the polynomial f (x) = 2x4 – 3x3 - 3x2 +6x – 2, if being given that, two of its zeros are, , and -, , ., , Ans., , 15
Page 16 :
6. On dividing x3 – 3x2 + x + 2 by a polynomial g (x) the quotient and the remainder were, (x – 2) and -2x + 4 respectively, find g (x)., Ans., , 16
Page 17 :
7. Find all zeros of f(x) = 2x3 - 7x2 + 3x + 6 if its two zeros are -, , and, , ., , Ans., , 17
Page 18 :
8. Obtain all zeros of the polynomial f (x) = 2x4 + x3 - 14x2 – 19x – 6, if two of its zeros are, -2 and -1., Ans., , 18
Page 20 :
11. Find the value of ‘k’ for which the polynomial x4 + 10x3 + 25x2 + 15x + k is exactly, divisible by (x + 7)., Ans., , 12. If, , and, , are the zeros of the polynomial f (x) = x2 + px + q, find polynomial, , 20
Page 21 :
whose zeros are (, , +, , )2 and (, , -, , )2., , Ans., , 21
Page 22 :
CBSE Class 10 Mathematics, Important Questions, Chapter 2, Polynomails, , 4 Marks Questions, 1. Divide the polynomial p(x) by the polynomial g(x) and find the quotient and, remainder in each of the following., (i) p(x) = x3 − 3x2 + 5x − 3, g(x) = x2 − 2, (ii) p(x) = x4 − 3x2 + 4x + 5, g(x) = x2 – x + 1, (iii) p(x) = x4 − 5x + 6, g(x) = 2 − x2, Ans. (i), , Therefore, quotient =x – 3and Remainder =7x – 9, (ii), , 22
Page 24 :
(ii), , Remainder = 0, Hence first polynomial is a factor of second polynomial., (iii), , Remainder ≠0, Hence first polynomial is not factor of second polynomial., , 3. Obtain all other zeroes of (3x4+6x3−2x2−10x−5), if two of its zeroes are, , Ans. Two zeroes of (3x4+6x3−2x2−10x−5) are, , and, , and, , ., , which means that, , 24
Page 26 :
p(x)=g(x).q(x)+r(x), ⇒x3−3x2+x+2 = g(x).(x−2)−2x+4, ⇒x3−3x2+x+2+2x−4=g(x).(x−2), ⇒x3−3x2+3x−2=g(x).(x−2), ⇒g(x)=, , So, Dividing (x3−3x2+3x−2) by (x−2), we get, , Therefore, we have g(x)=, , =x2−x+1, , 5. Give examples of polynomials p(x), g(x), q(x) and r(x), which satisfy the division, algorithm and, (i) deg p(x)=deg q(x), (ii) deg q(x)=deg r(x), (iii) deg r(x)=0, Ans. (i) Let p(x)=3x2+3x+6, g(x)=3, , 26
Page 27 :
So, we can see in this example that deg p(x)=deg q(x)=2, (ii) Let p(x)=x3+5 and g(x)=x2−1, , We can see in this example that deg q(x)=deg r(x) =1, (iii) Let p(x)=x2+5x−3, g(x) =x+3, , We can see in this example that deg r(x)=0, , 6. Find the zeroes of the following quadratic polynomials and verify the relationship, , 27
Page 28 :
between the zeros and the coefficients., (i) x 2 −2x−8, (ii) 4s2−4s+1, (iii) 6x2−3−7x, (iv) 4u2+8u, (v) t 2 −15, (vi) 3x2−x−4, Ans. (i) x2−2x−8, Comparing given polynomial with general form ax2+bx+c,, We get a=1, b=-2 and c=-8, We have, x2−2x−8, =x2−4x+2x−8, =x(x−4)+2(x−4)=(x−4)(x+2), Equating this equal to 0 will find values of 2 zeroes of this polynomial., (x−4)(x+2)=0, ⇒ x=4,−2 are two zeroes., Sum of zeroes =4 – 2=2 =, , =, , Product of zeroes =4×−2=−8 =, , (ii) 4s2−4s+1, , 28
Page 30 :
⇒ x=, , Therefore, two zeroes of this polynomial are, , Sum of zeroes=, , Product of Zeroes =, , (iv) 4u2+8u, Here, a=4, b=8 and c=0, 4u2+8u = 4u(u+2), Equating this equal to 0 will find values of 2 zeroes of this polynomial., ⇒ 4u(u+2)=0, ⇒ u=0,−2, Therefore, two zeroes of this polynomial are 0,−2, Sum of zeroes =0−2=−2 =, , =, , Product of Zeroes =0×−2=0 =, , (v) t2−15, Here, a=1, b=0 and c=-15, We have, t2−15, ⇒ t2=15, , 30
Page 31 :
⇒ t=, , Therefore, two zeroes of this polynomial are, , Sum of zeroes=, , Product of Zeroes =, , (vi) 3x2−x−4, Here, a=3, b=-1 and c=-4, We have, 3x2−x−4=3x2−4x+3x−4, =x(3x−4)+1(3x−4)=(3x−4)(x+1), Equating this equal to 0 will find values of 2 zeroes of this polynomial., ⇒ (3x−4)(x+1)=0, ⇒ x=, , Therefore, two zeroes of this polynomial are, , Sum of zeroes=, , Product of Zeroes =, , 7. Find a quadratic polynomial each with the given numbers as the sum and product of, , 31
Page 32 :
its zeroes respectively., (i), , , −1, , (ii), , ,13, , (iii) 0,, , (iv) 1, 1, (v), , (vi) 4, 1, Ans. (i), , , −1, , Let quadratic polynomial be ax2+bx+c, Let α and β are two zeroes of above quadratic polynomial., α+β =, , α× β=-1, , =, , =, , Quadratic polynomial which satisfies above conditions= 4x2−x−4, (ii), , Let quadratic polynomial be ax2+bx+c, Let α and β be two zeros of above quadratic polynomial., , 32
Page 34 :
Quadratic polynomial which satisfies above conditions= x2−x+1, (v), , Let quadratic polynomial be ax2+bx+c, Let α and β be two zeros of above quadratic polynomial., α+β=, , α× β=, , =, , =, , Quadratic polynomial which satisfies above conditions= 4x2+x+1, (vi) 4, 1, Let quadratic polynomial be ax2+bx+c, Let α and β be two zeros of above quadratic polynomial., α+β=4, , α× β= 1, , =, , =, , Quadratic polynomial which satisfies above conditions= x2−4x+1, , 8. Verify that the numbers given alongside of the cubic polynomials below are their, , 34
Page 35 :
zeroes. Also verify the relationship between the zeroes and the coefficients in each, case:, (i), , (ii), , Ans. (i) Comparing the given polynomial with, , , we get, , and, , =, , =, , =0, , =, , =0, , =, =, , =0, and, , Now,, , are the zeroes of, , =, , And, , 35
Page 36 :
=, , =, , And, , =, , =, , (ii) Comparing the given polynomial with, , , we get, , and, , =, , =0, , =, , =0, and, , are the zeroes of, , Now,, , =, , And, , =, , And, , =, , =, , =, , 9. Find a cubic polynomial with the sum of the product of its zeroes taken two at a time, and the product of its zeroes are, Ans. Let the cubic polynomial be, , respectively., and its zeroes be, , and, , 36
Page 37 :
Then, , =2=, , and, , =, , And, , =, , Here,, , and, , Hence, cubic polynomial will be, , 10. If the zeroes of the polynomial, Ans. Since, , are, , find, , and, , are the zeroes of the polynomial, , =, , And, =, , 37
Page 38 :
Hence, , and, , ., , 11. If the two zeroes of the polynomial, , are, , find, , other zeroes., Ans. Since, , are two zeroes of the polynomial, , Let, , Squaring both sides,, , Now we divide, , by, , to obtain other zeroes., , =, =, =, , 38
Page 39 :
=, and, , are the other factors of, , and 7 are other zeroes of the given polynomial., , 12. If the polynomial, , is divided by another polynomial, , the remainder comes out to be, Ans. Let us divide, , find, by, , and, ., , Remainder =, On comparing this remainder with given remainder, i.e., , And, , 39