Page 1 :
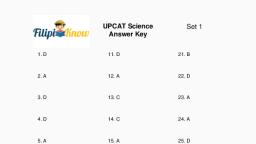
Set 2, , UPCAT, Mathematics, Answer Key, 1. Answer: C., , This question is really asking for the perimeter of the field. Add up all of the sides to find the, perimeter:, (125 * 2) + (200 * 2) = 650, , 2. Answer: B., Only one line can pass through a point and be parallel to an existing line., , 3. Answer: B., An infinite number of lines can pass through any given point in space—only one line can pass, through a point and be perpendicular to an existing line. In this case, that point is on the line;, however, this rule also applies to points that are not on the line., , 4. Answer: A., When intersecting lines create right angles, they are perpendicular., , 5. Answer: B., Lines are straight; they cannot backtrack or bend (if they could bend, they would be a curve, not, a line). Consequently, when two lines intersect, they can share only one point., , 6. Answer: B., When two lines intersect, they share a single point in space. That point is technically on both, lines., , 7. Answer: D., In order to be a transversal, a line must cut across two other lines at different points. Line o, crosses lines m and l at the same point; it is not a transversal, , 8. Answer: A., To get more UPCAT review, materials,, visit https://filipiknow.net/upcatreviewer/, , To God be the glory!

Page 2 :
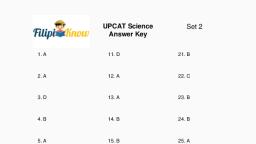
UPCAT, Mathematics, Answer Key, , Set 2, , One approach this question is to draw it., , For the resulting parallelogram A'BAC, length c will not be included in the perimeter (since CB is, the diagonal of the parallelogram, not a side)., All the answer choices with length c can be eliminated -- which leaves us with just (A) and (E)., The perimeter can be found by adding up the lengths of the sides:, a+a+b+b, = 2a + 2b, = 2(a + b), , 9. Answer: C., 1, 2, , Write the applicable formula. A = h(b1 + b2), A = 7,200, b1 = 40, b2 = 80, h=?, 1, 2, , Substitute the given values into the formula: 7,200 = · h · (40 + 80), 1, , Simplify the expression: 7,200 = · h · 120 7,200 = 60 h, 2, , Divide both sides of the equation by 60., , 7200, 60, , =, , 60ℎ, 60, , Simplify the expression. 120 = h, Include the units. 120 ft = h, , 10. Answer: D., To get more UPCAT review, materials,, visit https://filipiknow.net/upcatreviewer/, , To God be the glory!

Page 3 :
UPCAT, Mathematics, Answer Key, , Set 2, , Write the applicable formula. V = πr2h, List the values for the variables., V = 13,565, r = 12, h=?, π = 3.14, Substitute the given values into the formula. 13,565 = (3.14)(12 2)h, Simplify the expression. 13,565 = 452.16h, Divide both sides of the equation by 452.16., 13565, 452.16, , =, , 452.16ℎ, 452.16, , Simplify the expression. 30 = h, Include the units. 30 feet = h, , 11. Answer: B., Write the applicable formula. S = 2πr(r + h), List the values for the variables., S = 2,512, r=x, h = 3x, π = 3.14, Substitute the given values into the formula. 2,512 = 2(3.14)(x)(x + 3x), Simplify the expression. 2,512 = 6.28x(4x), Divide both sides of the equation by 25.12., 2,512, 25.12𝑥2, =, 25.12, 25.12, Simplify the expression., 100 = x2, Solve for x., , To get more UPCAT review, materials,, visit https://filipiknow.net/upcatreviewer/, , To God be the glory!

Page 4 :
UPCAT, Mathematics, Answer Key, , Set 2, , 10 = x, Substitute the value for x into the values list., r = x = 10 feet, h = 3x = 3(10) = 30 feet, , 12. Answer: D., A right triangle has a right angle and two acute angles; it does not have any obtuse angles., , 13. Answer: A., The problem provides the lengths of two legs and an unknown angle. You could solve for a, hypotenuse using the Pythagorean theorem, and then use sine or cosine. But the least amount, of work uses what the question provides. Only the trigonometric ratio sin uses the lengths of two, legs. Divide 13.9 by 20 and match the answer on the chart., , 14. Answer: B., Horizontal lines are of the form y = constant and vertical lines are of the from x = constant and, therefore the two lines are neither horizontal nor vertical. Let us find the slopes of the two given, lines, y = 2x has a slope equal to 2, 2y = - x is equivalent to y = -(1/2) x and its slope is equal to -(1/2) Since the slopes are not, equal, the two lines are not parallel. The product of the two slopes is given by, 2*-(1/2) = - 1, and hence the two lines are perpendicular., , 15. Answer: D., Let 2r = radius of smallest circle and 5r = radius of the largest circle, Asmall = 𝜋 (2r)2, 36 𝜋 = 4 𝜋r2, , To get more UPCAT review, materials,, visit https://filipiknow.net/upcatreviewer/, , To God be the glory!

Page 5 :
UPCAT, Mathematics, Answer Key, , Set 2, , 9 = r2, 3=r, Alarge = 𝜋 (5r)2, = 𝜋 (5 x 3)2, = 𝜋 (15)2, = 225 𝜋, , 16. Answer: D., A line, a line segment, and a ray are sets of points. How many points make a set? An infinite, number. Since a limit cannot be put on infinity, not one of the answer choices has more than the, other., , 17. Answer: D., Always assume that in plane geometry a line is a straight line unless otherwise stated. Process, of elimination works well with this question: Lines have one dimension, length, and no, substance; they are definitely not solid. Lines extend to infinity; they are not finite. Finally, we, defined noncollinear as a set of points that “do not line up”; we take our cue from the last part of, that statement. Choice c is not our answer., , 18. Answer: D., Collinear points are also coplanar. Choice a is not the answer because noncollinear points, determine planes, not a single line of collinear points., , 19. Answer: B., A line segment is the shortest distance between any two points., , 20. Answer: B., , To get more UPCAT review, materials,, visit https://filipiknow.net/upcatreviewer/, , To God be the glory!

Page 6 :
UPCAT, Mathematics, Answer Key, , Set 2, , A = LW, (6 √3 )(2√3), 12 (3) = 36, , 21. Answer: A., Three noncollinear points determine a plane. In this case, we know level X is a plane and Ann,, Bill, and Carl represent points on that plane. Ann and Bill together are not enough points to, define the plane; Dan isn’t on plane X and choice d doesn’t make sense. Choice a is the only, option., , 22. Answer: D., Unlike a plane, an office floor can hold only so many people; however, imagine the office floor, extending infinitely in every direction. How many people could it hold? An infinite number., , 23. Answer: D., Just as the office floor can represent a plane, Ann and Bill can represent points. They acquire, the characteristics of a point; and as we know, points have no dimension, and two points make, a line., , 24. Answer: B., Ann, Bill, and Carl are all on the same floor, which means they are all on the same plane, and, they are not lined up. That makes them noncollinear but coplanar., , 25. Answer: D., To get more UPCAT review, materials,, visit https://filipiknow.net/upcatreviewer/, , To God be the glory!

Page 7 :
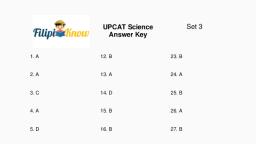
Set 2, , UPCAT, Mathematics, Answer Key, , Carl and Dan represent two points; two points make a line; and all lines are collinear and, coplanar. Granted, Dan and Carl are on two different floors; but remember points exist, simultaneously on multiple planes., , 26. Answer: B., Let r be the radius of the semicircle. Area of the semicircle is known; hence, 1250Pi = (1/2) Pi r2 (note the 1/2 because of the semicircle), Solve for r: r = 50, Length of rectangle = 2r = 100 (semicircle inscribed), Width of rectangle = r = 50 (semicircle inscribed), Area = 100 * 50 = 5000, , 27. Answer: D., Recall that the circumference is the distance around a circle. If the cake is divided into 12 equal, slices, each arc length will be 5. Summing 5 of these slices will give 25., , 28. Answer: C., Since vertical angles are congruent, the angle vertical to the 35- degree angle also has a, measure of 35 degrees. The supplement of the 120-degree angle has a measure of 60 degrees,, so we then have a triangle with angles measuring 35, 60, and x degrees, as shown in the figure, provided. Since the angles of a triangle add to 180 degrees:, 35 + 60 + x = 180, x = 180 − 35 − 60, x = 85 degrees, , 29. Answer: B., Solve this by process of elimination., A: True: AB and EF are both perpendicular to line BCF., C: True: Angle F is a right angle, so the two lines are perpendicular., D: True: Angle BCA and angle DCF are vertical angles, so they must be equal., E: True: Angle ABC = angle CDF (they are both right angles)., To get more UPCAT review, materials,, visit https://filipiknow.net/upcatreviewer/, , To God be the glory!

Page 8 :
UPCAT, Mathematics, Answer Key, , Set 2, , Angle BCA = angle DCF (see statement D). Therefore, angle BAC must equal angle DFC (since, the other two angles are equal, and the three angles total to 180). Since the two triangles have, three corresponding angles, they are similar. B can be false., Although we know that triangles ABC and CDF are similar, we do not know that they are, congruent. So these sides may be unequal., , 30. Answer: A., Recall that the angles of a triangle sum to 180 degrees:, 3x + 10 + −2x + 40 + x + 40 = 180, 2x + 90 = 180, 2x = 90, x = 45, , 31. Answer: B., As this question requires a couple spatial relationships, it may prove useful to draw a picture, representing the situation. We are given that the diameter, which is the same as the diagonal of, a cube, is equal to 5 inches. We also know that the diagonal of a cube is the hypotenuse of the, right triangle constructed from one of the cube’s side lengths as well as the diagonal of one of, the square faces of the cube., Using this information we will set up an equation for the known relationships (Pythagorean’s, Theorem) before solving for the target variable s, which represents the cube’s side length. We, know that the hypotenuse of a cube’s square face is s√2 (recall that 45°, 45°, 90° right triangles, have a side length relationship of x, x, x√2). We also know that one side length of the cube is s., Consequently:, , To get more UPCAT review, materials,, visit https://filipiknow.net/upcatreviewer/, , To God be the glory!

Page 9 :
UPCAT, Mathematics, Answer Key, , Set 2, , However, this answer choice is not found, so we must remove the radical from the denominator:, , 32. Answer: D., If a triangle has side lengths a, b, and c, the sum of the lengths of any 2 sides must be larger, than the length of the 3rd side. So in this case, 5 + 6 = 11 must be larger than side length c., From the answer choices, 12 is the only length greater than 11, so it cannot be the length of the, third side., , 33. Answer: C., The circumference of a circle is the distance around defined by π * diameter. The diameter, in, this case, can be found through the difference between the x values:, 3 − (−3) = 6, so π * 6 is the circumference., , 34. Answer: D., A square is a rhombus and a rectangle. Therefore, some rhombuses are rectangles., , 35. Answer: C., Problems involving similar figures can be solved using proportions. The issue with this problem, is that we are given a similarity across inches to feet with the answer choices containing only, inches. First, we must convert the feet measurement into inches:, 2 1/3 ft. x 12 in./ft. = 28 in., We can now set up our proportions:, To get more UPCAT review, materials,, visit https://filipiknow.net/upcatreviewer/, , To God be the glory!

Page 10 :
UPCAT, Mathematics, Answer Key, , Set 2, , 4/7 = x/28, x = 16, , 36. Answer: B., Sometimes questions will provide unnecessary information. In this case, the angle, measurement of the top right angle. We can focus exclusively on the right triangle shown and, use the Pythagorean Theorem, or the recognition of a Pythagorean triple to see that the length, of y is 8 cm., , 37. Answer: C., Choice A is not an acute triangle because it has one right angle. In choice B, the sum of interior, angle measures exceeds 180°. Choice D suffers the reverse problem; its sum does not make, 180°. Though choice C describes an equilateral triangle; it also describes an isosceles triangle., , 38. Answer: C., The trigonometric ratios sine and cosine never equal or exceed 1.000 because the hypotenuse,, the longest side of a right triangle, is always their denominator. The trigonometric ratio Tangent, can equal and exceed the value 1.000 because the hypotenuse is never its denominator., , To get more UPCAT review, materials,, visit https://filipiknow.net/upcatreviewer/, , To God be the glory!