Page 1 :
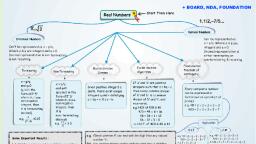
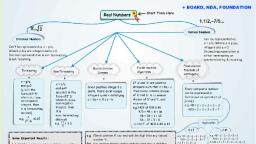
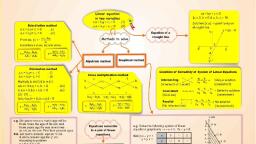
+ BOARD, NDA, FOUNDATION, Real Numbers, - Start From Here, 1,1/2,-7/5..., Rational Numbers, Can be represented as, x = p/q, Where p & q are, integers and q + 0., Decimal representation is, either terminating or, non-terminating & recurring, Irrational Numbers, Can't be represented as x = p/q,, Where p & q are integers and q # 0., Decimal representation is non terminating, & non-recurring., Fundamental, Euclid division, Euclid division, Terminating, Non-Terminating, Algorithm, theorem of, Lemma, Arithmetic, x = p/q, and q+0, (q is in the, form of 2 5, x = p/q, and q-0, (q is not in the, form of2" 5", where m, n are, Given positive integers a, and b, there exist unique, integers q and r satisfying, a = bq + r, 0sr< b., If 'a' and 'b' are positive, integers such that a = bq + r,, then every common divisor, of 'a' and 'b' is a common, Every composite number, can be expressed or, factorized as a product of, primes., e.g. 48 = 2 x 2 x 2 x 2 x 3, 420 = 2 x 2 x 3 x 5 x 7, where m, n are, divisor of 'b' and 'r', and, non-negative, integers, then, it is terminating, decimal), non-negative, vice-versa., e.g. HCF of 420 & 48, 420 = 48 x 8 36, 48 = 36 x 1 + 12, 36 12 x 3 +0, = H.C.F. of 420 & 48 is 12, integers, then, it is, 3, =0.15, 22 x5, non- terminating, decimal), 10 - 3.3, e.g., e.g., Application, H.C.F, L.C.M, e.g. 48 2 x 2 x 2 x 2 x 3, 420 = 2 x 2 x 3 x 5 x 7, L.C.M = 2 x 2 x 2 x 2 x 3 x 5 x Z, = 1680, e.g. Check whether 6" can end with the digit 0 for any natural, e.g. 48 = 2 x 2 x 2 x 2 x 3, 420 = 2 x 2 x 3 x 5 x 7, H.C.F = 2 x 2 x 3, Some Important Results:, number 'n'., Sol. Any positive integer ending with the digit zero is divisible, by 5 and so its prime factorization must contain the prime 5., 6 = (2 x 3) = 2" x 3", 1. Let 'p' be a prime number and 'a' be a positive, integer. If 'p' divides a', then 'p' divides 'a'., H.C.F. (48, 420) x L.C.M. (48,420), = 48 x 420, 2. HCF x LCM = Product of two numbers., The prime in the factorization of 6" is 2 and 3., 5 does not occur in the prime factorization of 6" for any n., (This is true for 2 numbers only), 3. LCM is always divisible by HCF., 6" does not end with the digit zero for any natural number n., NCERT / X / Real Number

Page 2 :
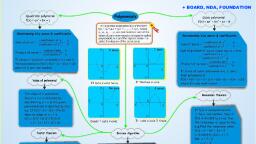
+ BOARD, NDA, FOUNDATION, Quadratic polynomial, f(x) = ax + bx +c, Polynomials, Cubic polynomial, f(x) = ax'+ bx' + cx + d, An algebraic expression f(x) of the form, f(x) = a, + a,x + a,x' . a,x', where, a,, a,, a,., a, are real numbers and all the, index of x are non-negative integers is called, polynomials in x and the highest Index n is, called the degree of the polynomial., Relationship b/w zeros & coefficients, Relationship b/w zeros & coefficients, -coefficient of x, b., Sum of zeros =, - coefficient of x2, b., coefficient of x2, Sum of zeros =, coefficient of x, a, 2 zeros, YA, 1 zero, Sum of product of zeros taken two at a time, cons tant term, Product of zeros =, coefficientof, a, coefficient of x, coefficient of x, a, If zeros of quadratic polynomial is a and B, then polynomial is f(x) = k(x- (oa + B) x + B}, where k is any real number., --constant term, d, Product of zeroes =, 0., 0., coefficientof x, a, If zeros of cubic polynomial is a, B and y, then polynomial is, f(x) = k{x- (a + B+) x + (aß + By+ yo)x - 0By), where k is any real number., Value of polynomial, It touches x axis., It cuts x axis twice., No zero, 3 zeros, The value of a polynomial, f(x) at x = o is obtained by, substituting x = a in the given, polynomial and is denoted by f(a)., e.g. If f(x) = 2x'-13x+17x+12, then its value at x = 1 is, Remainder theorem, 0., If f(x) is a polynomial and, "a' be a real number, then if, f(x) is divided by (x-a), then, the remainder is equal to f(a)., e.g Find the remainder when, f(x) = x' +6x- 3x +5, is divided by g(x)% = x+2., Sol. x+2 = 0, YN, f(1) = 2(1)-13(1)+17(1)+12, = 2 - 13 +17 + 12 18., Doesn't cuts x axis., It cuts x axis 3 times., Factor theorem, Division Algorithm, >X= -2, If p(x) is a polynomial and 'a' be a, real number, such that p(a) = 0, then (x-a), is a factor of p(x)., e.g. Factors of f(x) = x - 3x +2 is (x-2)(x-1), f(1) = 1- 3(1) + 2 = 1-3+2= 0, & f(2) = 2- 3(2) + 2 = 4 - 6 + 2 = 0, Remainder = f(-2), = (-2)' + 6(-2)' - 3(-2) +5, = -8+ 24 + 6 + 5, = 27, Dividend = Divisior x Quotient + Remainder, OR, f(x) = g(x) x q(x) + r(x), Degree of q(x) = deg. f(x) - deg. g(x), Degree of r(x) < deg. g(x), NCERT / X/ Polynomial

Page 3 :
Linear equation, in two variables, .(1), ax + by + c = 0, {a = 0, b = 0 & a, b, ce R}, a,x + b,y + c, = 0, a,x + b.y + C, = 0 (2), Solution (x,y) point lying on, straight line., Substitution method, a,x + b,y+ c, = 0, a,x + b,y+ c, = 0, ..(i), ...(i), y = 2x – 4, Equation of a, YA, -C, -b;y, Methods to solve, straight line, From eq. (i) x =, a,, Substitute x in eq. (ii) and solve., 2,, X', 0., b,C2 -b2C1, a2C1 -aC2, -4, X =, y =, ab2 - azbi, a,b2 - azb,, Algebraic method, Graphical method, Y, Elimination method, Condition of Solvability of System of Linear Equations, ax + b,y+ c, = 0, ax + b,y+ c, = 0, ..(i), ...(i), Cross multiplication method, by, b2, y, 1, Intersecting, Unique solution, (consistent), b,, Multiply b, in (i) & b, in (ii), a,b,x+ b,b.y + c, b, = 0, b, a,x + b,b.y + c,b, = 0, (3) -(4).., (a,b,-b,a,)x + (c,b,-c,b,) = 0, 'D4, a2, (intersect at 1 point), .(ii), .(iv), b,, b,, - Infinite solution, C2, (consistent), Coincident, %3D, a2, b2, (Coincide), b;c2 -b2C, C,a2 - aC2, a,b2 - azb,, b1, C1, b2, → No solution, C2, Parallel, a2C1 -aC2, b;C2-b2C1, a,b2-a2b,, a2, X =, b;C2 -b2C1, y =, a2C-aC2, y =, (No intersection), (inconsistent), a,b2 - azb,, ab2 - azb,, ab2 -azb1, у-ахis, e.g. Six years hence a man's age will be, three times the age of his son and, three years ago he was nine times, as old as his son. Find their present ages., Sol. Let man's present age be 'x' yrs, & son's present age be 'y' yrs., According to problem, x + 6 = 3 (y + 6), x- 3y = 12... (i), and x - 3 = 9 (y-3), x- 9y = - 24... (ii), On solving equation (i) & (ii), x = 30 and y = 6., So, the present age of man = 30 years, and present age of son = 6 years., (0, 8), e.g. Solve the following system of linear, equations graphically : x- y = 1, 2x + y = 8., Equations reducible, to a pair of linear, 7, equations, 1, 2, 6, (1, 6), Sol.(i) x-y = 1, x = y + 1, y, - 1, (2, 4), (ii) 2x + y = 8, y = 8 - 2x, 3, A, 2 3, -+== 13,, x y, Let, 5 4, = -2, y, 1, (3, 2), y, 6, 4, (2,1), x' +, 2p + 3q 13, 5p - 4q = -2, ++, 2 3, 1, Solution is x 3 and y = 2, 1, -=p,, y, 4, X-axis, (0,-1), NCERT / X / Linear equation in two variable

Page 4 :
Quadratic Equations, Application, Nature of roots, An equation of the form ax' + bx +c 0,, where a,b,c are real numbers and a = 0, is, called a quadratic equation in x., ax + bx + c = 0, where a = 0, D = (b - 4ac). and the roots are, given by, Dis tan ce, 1. Speed =, Time, 2. Area of figures, 3. Flow rate x time volume of water, 4. Number or ages, -b+ VD, -b- D, Solution or Roots of Quadratic Equation, A real number a is called a root of the, quadratic equation ax + bx +c = 0, a 0 if, ao + ba + c = 0, and B, 2a, 2a, Case - I, When D > 0, roots are real distinct, and given by, -b+ VD, =, -b- VD, e.g. The hypotenuse of a right triangle is 25 cm., The difference between the, and B, 2a, %3D, 2a, of the other two, Case - II, When D = 0, roots are real and equal, and roots are given by, Method of, sides of the triangle is 5 cm. Find the lengths of these sides., Sol. Shorter side = x cm, longer side (x + 5) cm., hypotenuse = 25 cm, by pythagoras Theorem, x + (x + 5) = 25, x + 5x - 300 = 0, (x+ 20)(x - 15) = 0, This gives x = 15 or x = - 20., We reject x = - 20 and take x = 15., Thus, length of shorter side = 15 cm., Length of longer side = (15 + 5) cm, i.e., 20 cm., finding solution, a =B=-, 2a, Completing the square method, Case - III, When D « 0, roots are not real., ax' + bx + c = 0, a 0., b., x2, +-x+-= 0, a, a, b., x+-x =, a, a, 2, b, x2., %3D, 2a, 2a, 2a, 12, b, 2, b, Factorisation method, 2a, 2a, a, In this method (ax + bx + c) be expressible, as the product of two linear expression, say, (px + q) and (rx + s), where p, q, r are real, numbers such that p +0 and r #0, Then ax + bx + c = 0 = (px + q) (rx + s) = 0, b., b2 - 4ac, %3D, 2a, 4a, Quadratic formula, for ax + bx + c = 0,, D = b' - 4ac, -bt D, b, b2-4ac, x+, =t,, 2a, 4a2, = (px + q)= 0 or (rx + s) 0, = x =-., or x =--, Obtain the values of x by shifting, 2a, on RHS, 2a, the constant term, NCERT / X/Quadratic Equation

Page 5 :
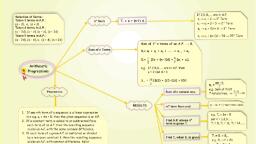
If 2,5,8,.. are in A.P., a, → a, = 2 → 1" Term, a, → a, + d = 5 2nd Term, Selection of Terms :, Taken 3 terms in A.P. :, nh Term, T. = a +, (n-1) d., (a - d), a, (a+ d), Taken 4 terms in A.P. :, a, a, + 2d = 8 3rd Term, (a - 3d), (a - d), (a + d), (a + 3d), Taken 5 terms in A.P. :, a, → a, + (n-1)d = 74 → 25th Term, (a - 2d), (a - d), a, (a + d), (a + 2d), Sum of 1" n terms of an A.P. → S,, Sum of n Terms, S,= a, + a, + a, + .... + a. 1 + a,., " (2a + (n-1)d] =" [a, + a.)., S. 2, %3D, Arithmetic, Progressions, e.g. If 2,5,8,. are in A.P. then, a = 2 and d = 3, S25 = 25 [2(2) (25-1)3] = 950, 2, n(n+1), e.g. Sum of first, 7x8, PROPERTIES, Sum of n natural nos., 7 natural nos. =, = 28, RESULTS, mt term from end, (n - m + 1)" term from start, 1. If any nth term of a sequence is a linear expression, in n e.g. a, = An + B, then the given sequence is an A.P., 2. If a constant term is added to or subtracted from, each term of an A.P. then the resulting sequence, is also an A.P. with the same common difference., 3. If each term of a given A.P. is multiplied or divided, by a non-zero constant K, then the resulting sequence, is also an A.P. with common difference Kd or, respectively. Where d is the common difference of, the given A.P., 4. In a finite A.P. the sum of the terms equidistant from, the beginning and end is always same and is equal, to the sum of 1st and last term., e.g. T, = 3n + 5, put n = 1,2,3.., T = 8, T, = 11, T, = 14..., Find A.P. whose n", term is given ?, T, = S, - S, e.g. S, = n' + 2n, .. T, = 2n + 1, Find T, when S, is given, Condition of an A.P., If a, b, c are 3 terms, of an A.P. then :, a +c = 2b., NCERT / X/ Arithmatic progression