Page 2 :
SSLC Mathematics Solutions – Part -1, , YK, , Contents, Part -1, Sl.No., , Chapters, , Page No., , 1, , Arithmetic Progression, , 2, , Triangles, , 32 - 62, , 3, , Pair of Linear equation in two variables, , 63 - 98, , 4, , Circles, , 5, , Area Related to circles, , 108 - 122, , 6, , Constructions, , 123 - 132, , 7, , Coordinate Geometry, , 133 - 149, , 8, , Real Numbers, , 150 - 159, , P a g e 1 | 159 Available in ykoyyur.blogspot.com, , 1 - 31, , 99 - 107

Page 3 :
SSLC Mathematics Solutions – Part -1, , YK, , Arithmetic progression, 1.2 Arithmetic Progressions:, An arithmetic progression is a list of numbers in which, each term is obtained by adding a fixed number to, the preceding term except the first term., , i), , 1, 2, 3, 4 ................., , each term is 1 more than the term preceding it., , ii), , 100, 70, 40, 10 ........, , each term is 30 less than the term preceding it., , iii) -3, -2, -1, 0 .............., iv) 3, 3, 3, 3 ................, v), , -1, -1.5,-2.0,-2.5, ......., , each term is obtained by adding 1 to the term preceding it., all the terms in the list are 3 , i.e., each term is obtained by, adding(or subtracting) 0 to the term preceding it., each term is obtained by adding – 0.5 to (i.e., subtracting 0.5, from) the term preceding it., , This fixed number is called the common difference of the AP. Remember that it can be positive,, negative or zero., , Let us denote the first term of an AP by a1, second term by a2,, . . ., nth term by an and the common difference by d. Then, the AP becomes a1, a2, a3, . . ., an., So, a2 – a1 = a3 – a2 = . . . = an – an – 1 = d, a, a + d, a + 2d, a + 3d, . . ., Represents an arithmetic progression where a is the first term, and d the common difference. This is called the general form, of an AP., Finite AP.:, In an AP there are only a finite number of terms. Such an AP is called a finite AP. Each, of these Arithmetic Progressions (APs) has a last term., a) The heights ( in cm ) of some students of a school standing in a queue in the morning, assembly are 147 , 148, 149, . . ., 157., b) The balance money ( in Rs ) after paying 5 % of the total loan of Rs 1000 every month, is 950, 900, 850, 800, . . ., 50., c) The total savings (in Rs ) after every month for 10 months when Rs50 are saved each, month are 50, 100, 150, 200, 250, 300, 350, 400, 450, 500., , P a g e 2 | 159 Available in ykoyyur.blogspot.com

Page 4 :
SSLC Mathematics Solutions – Part -1, , YK, , Infinite AP.:, In an AP there are infinite number of terms. Such an AP is called a infinite AP. Each of, these Arithmetic Progressions (APs) do not have last term., a) 3, 7, 11, . . . ., b) 1, 4, 7, 10, . . ., c) -10, -15, -20, . . . ., Note: You will If we know the first term a’ and the common difference d’ then we can, write an AP., Example 1: , , − , − ........... write the first term a and the common difference d., Here,, = d=, =, = -1, =− = -1, Example 2 : Which of the following list of numbers form an AP? If they form an AP,, write the next two terms, i) 4, 10, 16, 22 ........, ii) 1, -1, -3, -5 ........, iii) -2, 2, -2, 2 ........, iv) 1, 1, 1, 2, 2, 2, 3, 3, 3 .........., Solution :, i) 4, 10, 16, 22 ........, - = 10 – 4 = 6, - = 16 – 10 = 6, - = 22 – 16 = 6, i.e., ak + 1 – ak is the same every time., So, the given list of numbers forms an AP with the common difference d = 6. The next two, terms are: 22 + 6 = 28 and 28 + 6 = 34., ii) 1, -1, -3, -5 ........, - = -1 – 1 = -2, - = -3 – (-1) = -2, - = -5 – (-3) = -2, i.e., ak + 1 – ak is the same every time., So, the given list of numbers forms an AP with the common difference d = -2. The next two, terms are: – 5 + (– 2 ) = – 7 and – 7 + (– 2 ) = – 9, iii ) -2, 2, -2, 2 ........, - = 2 – (-2) = 2 + 2 = 4, - = -2 – 2 = -4, - = 2 – (-2) = 2 + 2 = 4, Here,, ≠, So, the given list of numbers does not form an AP., iv) 1, 1, 1, 2, 2, 2, 3, 3, 3 .........., - =1 – 1 =0, - =1 – 1 =0, - = 2 – 1 =1, - = ≠, - So, the given list of numbers does not form an AP., , P a g e 3 | 159 Available in ykoyyur.blogspot.com

Page 5 :
SSLC Mathematics Solutions – Part -1, , YK, , EXERCISE 1.1, 1. In which of the following situations, does the list of numbers involved make an arithmetic, progression, and why?, i). The taxi fare after each km when the fare is Rs15 for the first km and Rs 8 for each, additional km, The first term, = 15,, = 15 + 8 = 23 , = 23 + 8 = 31 ........., , Here, each term is obtained by adding a common difference = 8, except first term., ii). The amount of air present in a cylinder when a vacuum removes, remaining in the cylinder at a time., Let the initial volume of the air present in the cyclinder be V., The remaining air in the cylinder after using vacuum pump first time V - =, , of the air, , ,, , Remaining air in the cylinder after using vacuum pump second time, −, x = −, =, and so on., Here, the terms are V,, , ∴, , -, , =, , − V = −, , -, , =, , −, , -, , ≠, , =, , ,, −, , .. ….., = −, , -, , Hence, it does not form an AP, iii). The cost of digging a well after every metre of digging, when it costs Rs 150 for the first, metre and rises by Rs 50 for each subsequent metre., The cost of digging for the first meter = Rs 150, Cost of digging for the second meter = 150+50 = Rs 200, Cost of digging for the third meter = 200+50 = Rs 250, Cost of digging for the fourth meter = 250+50 = Rs 300, Thus the list of numbers is 150, 200, 250, 300........, Here, we can find the common difference = 50, So it forms an AP., iv). The amount of money in the account every year, when Rs 10000 is deposited at, compound interest at 8 % per annum., We know that amount A = P 1 +, Here, P = 10,000; r = 8%, n = 1,2,3…, Amount in first year = 10000 1 +, , = 10000x, , = 100x108 = Rs 10800, , Amount in second year = 10000 1 +, = 10000x x, = 108 x 108 = Rs 11664, Thus the list of numbers is 10000, 10800, 11664 .. ….., = 10800 − 10000 = 800, = 11664 − 10800 = 864, There for, ≠, Hence it does not form an AP., 2. Write first four terms of the AP, when the first term a and the common difference d are, given as follows:, P a g e 4 | 159 Available in ykoyyur.blogspot.com

Page 6 :
SSLC Mathematics Solutions – Part -1, , YK, , i) a = 10, d = 10, = 10,, = + d = 10 + 10 = 20, = + d = 20 + 10 = 30, = + d = 30 + 10 = 40, Thus the first four terms of an AP are 10, 20, 30, 40, ii) a = -2, d = 0, = -2,, = + d = -2 + 0 = -2, = + d = -2 + 0 = -2, = + d = -2 + 0 = -2, Thus the first four terms of an AP are -2, -2, -2, -2,, iii) a = 4, d = -3, = 4,, = +d=4-3= 1, = + d = 1 - 3 = -2, = + d = -2 - 3 = -5, Thus the first four terms of an AP are 4, 1, -2, -5, iv) a = -1, d =, = -1,, = + d = -1 +, = −, =, , +d=− +, , =, , =, , +d= 0 +, , =, , 0, , Thus the first four terms of an AP are -1, − , 0,, v) a = -1.25, d = -0.25, = -1.25, = + d = -1.25 - 0.25 = -1.50, = + d = -1.50 - 0.25 = - 1.75, = + d = -1.75 + 0.25 = -2.00, Thus the first four terms of an AP are -1.25, -1.50, -1.75, -2.00, 3. For the following APs, write the first term and the common difference:, i) 3, 1, - 1, - 3......., The first term a = 3,, Common difference d =, - = 1 – 3 = -2, ii) -5, -1, 3, 7......., The first term a = 5, Common difference d =, - = -1 – (-5) = -1 + 5 = 4, iii) , , , , . . . . ., The first term a =, Common difference d =, - = – =0, iv) 0.6, 1.7, 2.8, 3.9, ........, The first term a = 0.6, Common difference d =, - = 1.7 – 0.6 = 1.1, 4. Which of the following are APs ? If they form an AP, find the common difference d and, write three more terms, P a g e 5 | 159 Available in ykoyyur.blogspot.com

Page 7 :
SSLC Mathematics Solutions – Part -1, , YK, , i), , 2, 4, 8, 16 ........., - =4–2=2, - =8–4=4, Here,, - ≠ There fore the given list of numbers does not form an AP., ii) 2, , 3, ………, a -a = –2=, a -a =3– =, a -a = –3=, Here, a - a = a - a = Therefore the given list of numbers forms an AP with common difference d =, The next 3 terms of this AP are,, , + = 4; 4 + = ;, , + =5, , iii) -1.2, -3.2, -5.2, -7.2 ....., a - a = -3.2 – (-1.2) = -3.2 + 1.2 = -2, a - a = -5.2 – (-3.2) = -5.2 + 3.2 = -2, a - a = -7.2 – (-5.2) = -7.2 + 5.2 = -2, Here, a - a = a - a = a - a, Therefore the given list of numbers forms an AP with common difference d = −2, The next 3 terms of this AP are, -7.2 – 2 = -9.2 ; -9.2 – 2 = −11.2; −11.2 – 2 = -13.2, iv) -10, -6, -2, 2 ......, a - a = -6 – (-10) = -6 + 10 = 4, a - a = -2 – (-6) = -2 + 6 = 4, a - a = 2 – (-2) = 2 + 2 = 4, Here, a - a = a - a = a - a, Therefore the given list of numbers forms an AP with common difference d = 4, The next 3 terms of this AP are 2 + 4 = 6 ; 6 + 4 = 10; 10 + 4 = 14, i) 3, 3+ √ , 3 + √ , 3 + 3√ , ………, a - a = 3+ √2 – 3 = √2, a - a = 3 + 2√2 – 3+ √2= √2, a - a = 3 + 3√2 – 3 + 2√2 = √2, Here, a - a = a - a = a - a, Therefore the given list of numbers forms an AP with common difference d = √2, The next 3 terms of this AP are 3 + 3√2 + √2 = 3 + 4√2; 3 + 5√2; 3 + 6√2, ii) 0.2, 0.22, 0.222, 0.2222 ............., a - a = 0.22 – 0.2 = 0.02, a - a = 0.222 - 0.22 = 0. 002, Here, a - a ≠ a - a, There fore the given list of numbers does not form an AP., iii) 0, -4, -8, -12 ............, a - a = -4 – 0 = −4, P a g e 6 | 159 Available in ykoyyur.blogspot.com

Page 8 :
SSLC Mathematics Solutions – Part -1, a - a = -8 – (-4) = −8 + 4 = - 4, a - a = -12 – (-8) = −12 + 8 = -4, Here, a - a = a - a = a - a, Therefore the given list of numbers forms an AP with common difference, The next 3 terms of this AP are -12 – 4 = -16; -20; -24, iv) − , − , − , − , . . . . ., a -a =−, , – −, , =− + =0, , a -a =−, , – −, , =− + =0, , a -a =−, , – −, , =− + =0, , Here, a - a = a - a = a - a, Therefore the given list of numbers forms an AP with common difference, The next 3 terms of this AP are − , − , − ,, , YK, , d = -4, , d=0, , v) 1, 3, 9, 27 .........., a -a =3–1 =2, a -a =9–3 =6, Here, a - a ≠ a - a, There fore the given list of numbers does not form an AP., vi) a, 2a, 3a, 4a ........., a - a = 2a – a = a, a - a = 3a – 2a = a, a - a = 4a – 3a = a, Here,a - a = a - a = a - a, Therefore the given list of numbers forms an AP with common difference, d=a, The next 3 terms of this AP are 5a, 6a, 7a, vii) a, a2, a3, a4……., a - a = a2 – a = a(a − 1), a - a = a3 – a2 = a2(a – 1), Here,a - a ≠ a - a, There fore the given list of numbers does not form an AP., viii) √ , √ , √ , √ …….., a - a = √8 – √2 = 2√2 - √2 = √2, a - a = √18 – √8 = 3√2 - 2√2 = √2, a - a = √32 – √18 = 4√2 - 3√2 = √2, Here,a - a = a - a = a - a, Therefore the given list of numbers forms an AP with common difference d = √2, The next 3 terms of this AP are √50 , √72 , √98, ix) √ , √ , √ , √ ………., a - a = √6 – √3, a - a = √9 – √6 = 3 - √6, Here,a - a ≠ a - a, P a g e 7 | 159 Available in ykoyyur.blogspot.com

Page 9 :
SSLC Mathematics Solutions – Part -1, , YK, , There fore the given list of numbers does not form an AP., x) 1 1 , 32, 52, 72, ……, a - a = 32 – 1 1 = 9 – 1 = 8, a - a = 52 – 3 2 = 25 – 9 = 16, Here,a - a ≠ a - a, There fore the given list of numbers does not form an AP., xv) 11, 52, 72, 73, ………., a - a = 52 – 1 1 = 25 - 1 = 24, a - a = 72 – 5 2 = 49 - 25 = 24, a - a = 73 – 72 = 73 - 49 = 24, Here, a - a = a - a = a - a, Therefore the given list of numbers forms an AP with common difference d = 24, The next 3 terms of this AP are 73 + 24 = 97, 97 + 24 = 121, 121 + 24 = 145, , 1.3 nth Term of an AP, ′ Common difference is d' then the nth term, is, =, , +, , −, , nth term from the last n [ -last term ,, −, , −, , −, , Example 3 : Find the 10th term of the AP : 2, 7, 12, . . ., Solution : a = 2, d = 7 - 2 = 5 and n = 10, = + ( − 1), = 2 + (10 − 1)5, = 2 + (9)5, = 2 + 45, = 47, Example 4 : Which term of the AP : 21, 18, 15, . . . is – 81? Also, is any term 0? Give, reason for your answer., Solution: a = 21, d = 18 - 21 = -3 and, = -81. Now we have to find n, = + ( − 1), −81 = 21 + (n − 1)(-3), −81 = 21 − 3n + 3, −81 = 24 − 3n, 3n = 24 + 81 = 105, n = 35, which term is Zero?, 0 = 21 + (n − 1)(−3), P a g e 8 | 159 Available in ykoyyur.blogspot.com

Page 10 :
SSLC Mathematics Solutions – Part -1, , YK, , 0 = 21 − 3n + 3, 3n = 24, n=8, 8th term is Zero, Example 5 : Determine the AP whose 3rd term is 5 and the 7th term is 9., Solutin: + ( − 1) =, + (3 − 1) = 5, Alternate Method:, + 2 = 5 ------- (1), d=, + (7 − 1) = 9, a =a ;a =a, + 6 = 9 --------(2), +, = 5, d=, =, = =1, +, = 9, a=, + ( − 1) a, ( 7 − 1) 1, a, =, +, -4d = - 4, (, a = 9 + 7 − 1 )1, ⇒ d=1, a=9+6 =3, ⇒ + 2(1) = 5 ⇒ a + 2 = 5 ⇒ a = 5 – 2 = 3, ∴ AP: 3, 4, 5, 6, - - Example 6 : Check whether 301 is a term of the list of numbers 5, 11, 17, 23, . . ., Solution: a = 5, d = 11 – 5 = 6, + ( − 1) =, 5 + ( − 1)6 = 301, 5 + 6n − 6 = 301, 6n − 1 = 301, 6n = 301 + 1, 6n = 302, n =, =, Here n is not an integer, There fore 301 is not a term of the list of numbers 5, 11, 17, 13 ........., Example 7 : How many two-digit numbers are divisible by 3?, Solution: 12, 15, 18 ......99, a = 12, d = 3, an = 99, + ( − 1) =, 12 + ( − 1)3 = 99, 12 + 3n − 3 = 99, 3n + 9 = 99, 3n = 99 – 9, 3n = 90 ⇒ n = 30, There for 30 two digit numbers are divisible by 3., Example 8 : Find the 11th term from the last term (towards the first term) of the, AP : 10, 7, 4, . . ., – 62., Solution: a = 10, d = 7 - 10 = -3, l = -62, = + ( − 1), th, n term from the last = − ( − 1), = −62 − (11 − 1)(−3), = −62 + 33 − 3, = −62 + 30, = −32, P a g e 9 | 159 Available in ykoyyur.blogspot.com

Page 11 :
SSLC Mathematics Solutions – Part -1, , YK, , Example 9 : A sum of Rs 1000 is invested at 8% simple interest per year. Calculate the, interest at the end of each year. Do these interests form an AP? If so, find the interest at, the end of 30 years making use of this fact., Solution: The formula to calculate the simple intrest I =, So, the interest at the end of the 1st year =, , = Rs 80, , the interest at the end of the 2nd year =, , = Rs 160, , the interest at the end of the 3rd year =, There fore the terms are 80, 160, 240, - - -, , = Rs 240, , Here, - = - = d = 80, It is an AP as the difference between the consecutive terms in the list is 80,, The interest at the end of 30 years a n; a = 80, d = 80, n = 30, a = a + ( n − 1) d, a = 80 + (30 − 1)80, a = 80 + 29x80, a = 80 + 2320, a = Rs 2400, Example 10 : In a flower bed, there are 23 rose plants in the first row, 21 in the second,, 19 in the third, and so on. There are 5 rose plants in the last row. How many rows are, there in the flower bed?, Solution: The number of rose plants in the 1st, 2nd, 3rd, . . ., rows are :23, 21, 19,- - Here, - = - = -2, There fore it is an AP. a = 23, d = -2, an = 5, n = ?, + ( − 1) =, 23 + ( − 1)(−2) = 5, 23 − 2n + 2 = 5, −2n + 25 = 5, −2n = 5 – 25, −2n = −20, n = 10, So, there are 10 rows in the flower bed. = 10., , EXERCISE 1.2, 1. Fill in the blanks in the following table, given that a is the first term, d the common, n, difference and a the nth term, of the AP:, a, d, n, an, , (i), (ii), (iii), (iv), (v), i), a, a, a, , 7, − 18, 46, − 18.9, 3.5, , 3, 2, −3, 2.5, 0, , 8, 10, 18, 10, 105, , = +( − ), = 7 + (8 − 1)3, = 7 + 7x3, = 7 + 21, , P a g e 10 | 159 Available in ykoyyur.blogspot.com, , 28, 0, −5, 3.6, 3.5

Page 12 :
SSLC Mathematics Solutions – Part -1, a = 28, i) a = a + (n − 1)d, 0 = −18 + (10 − 1)d, 0 = −18 + 9d, 9d = 18, d = 2, ii), = +( − ), −5 = a + (18 − 1)(−3), −5 = a − 17x3, −5 = a – 51, a, = 46, iii), = +( − ), 3.6 = −18.9 + (n − 1)(2.5), 3.6 = −18.9 + 2.5n − 2.5, 3.6 = −21.4 + 2.5n, 2.5n = 3.6 + 21.4, n =, =, = 10, ., iv), = +( − ), a = 3.5 + (105 − 1)(0), a = 3.5 + 104x0, a = 3.5, 2. Choose the correct choice in the following and justify :, (i) 30th term of the AP: 10, 7, 4, . . . , is, = + ( − 1), d = a - a = 7 – 10 = -3, a = 10 + (30 − 1)(−3), a = 10 + (29)(−3), a = 10 − 87, a = −77, (A), 97 (B) 77 (C), -77, (D) -87, th, (ii) 11 term of an AP: -3, - , 2, ..... is, a = a + (n − 1)d, d = a - a = - – (-3) = - + 3 =, 5, a = −3 + (11 − 1), 2, 5, a = −3 + (10), 2, a = −3 + 25, a = 22, (A), 28 (B) 22 (C) -38, (D), -48, 3. In the following APs, find the missing terms in the boxes :, i), , 2, , 14 ,, 26, , ii), , ,, 18 ,, 13,, , iii) ,, 5, ,, 6 ,, , 8 ,, 3,, 8 ,,, 9 ,, , P a g e 11 | 159 Available in ykoyyur.blogspot.com, , YK

Page 13 :
SSLC Mathematics Solutions – Part -1, iv),, -4,,, -2 , , 0 , , 2, , ,, 4, , ,,, 6, , v) ,, 53,,,, 38,,, 23, , ,, 8, ,,, -7, , −22, 4. Which term of the AP : 3, 8, 13, 18, . . . ,is 78?, Solution:a = a + (n − 1)d, d = a - a = 8 – 3 = 5; a = 3; an = 78; n = ?, 78 = 3 + (n − 1)5, 78 = 3 + 5n − 5, 78 = 5n − 2, 5n = 78 + 2, 5n = 80, n = 16, 5. Find the number of terms in each of the following APs :, Solution: i) 7, 13, 19 ....... 205, a = a + ( n − 1) d, d = a - a = 13 – 7 = 6; a = 7; an = 205; n = ?, 205 = 7 + (n − 1)6, 205 = 7 + 6n − 6, 205 = 6n + 1, 6n = 205 − 1, 6n = 204, n =, n = 34, (ii) 18, 15 , 13 ....... -47, a = a + ( n − 1) d, d = a - a = 15 – 18 =- ; a = 18; an = -47; n = ?, 5, −47 = 18 + (n − 1) −, 2, 5, 5, −47 = 18 − n +, 2, 2, 36 − 5n + 5, −47 =, 2, 41 − 5n, −47 =, 2, −94 = 41 − 5n, −5n = −94 − 41, −5n = −135, n, = 27, 6. Check whether – 150 is a term of the AP : 11, 8, 5, 2 . . ., Solution:a = a + (n − 1)d, d = a - a = -3; a = 11; an = 150; n = ?, −150 = 11 + (n − 1)(−3), −150 = 11 − 3n + 3, −150 = 14 − 3n, −3n = −150 − 14, −3n = −164, P a g e 12 | 159 Available in ykoyyur.blogspot.com, , YK

Page 14 :
SSLC Mathematics Solutions – Part -1, , YK, , 164, 3, n is not an integer. So, -150 is not a term of the AP: 11, 8, 5, 2, .., 7. Find the 31st term of an AP whose 11th term is 38 and the 16th term is 73., Solution:a = a + (n − 1)d, Alternate Method:, a, = 38, a = 73, a = ?, d=, a + (11 − 1)d = 38, a =a ;a =a, a + 10d = 38 ---------------(1), a + (16 − 1)d = 73, d=, =, = =7, a + 15d = 73 ----------------(2), =, +( − ) a, from (1) and (2), =, + ( 31 − 16)7, +, =, = 73 + ( 15)7, +, =, = 73 + 105 = 178, -5d = -35, d =, =7, n =, , (1) ⇒ a + 10x7 = 38, ⇒ a + 70 = 38, ⇒ a = 38 − 70, ⇒ a = −32, a, = −32 + (31 − 1)7, a, = −32 + (30)7, a, = −32 + 210, a, = 178, 8. An AP consists of 50 terms of which 3rd term is 12 and the last term is 106. Find the 29th, term.50, Solution:a + (n − 1)d = a, n = 50, a = 12, a = 106 a = ?, a + (50 − 1)d = 106, a + 49d = 106 -------- (1), a + 2d = 12 -------- -(2), +, =, +, =, 47d = 94, ⇒d = 2, Substitute d = 2 in eqn (2), a + 2(2) = 12, a + 4 = 12, a = 12 - 4, , Alternate MethodÀ:, d=, a =a, d=, , ;a =a, , =, = =2, =, +( − ) a, = + ( 29 − 3)2, = 12 + ( 26)2, = 12 + 52 = 64, , a = 8, a = 8 + (29 − 1)2, a = 8 + (28)2, a = 8 + 56, a = 64, 9. If the 3rd and the 9th terms of an AP are 4 and – 8 respectively, which term of this AP is, zero?, P a g e 13 | 159 Available in ykoyyur.blogspot.com

Page 15 :
SSLC Mathematics Solutions – Part -1, , YK, , Solution:a = 4, a = −8, Alternate methodÀ:, an = a + (n − 1) d, d=, a3 = a + (3 − 1) d, 4 = a + 2d ------------(i), a =a ;a =a, a9 = a + (9 − 1) d, d=, =, =, = -2, −8 = a + 8d ---------- (ii), =, + ( − 1) a, Substract (i) from (ii),we get, = + ( 3 − 1)(−2), −12 = 6d ⇒ d = −2, = 4 + ( 2)(−2), From equation (i),, 4 = a + 2 (−2), =4−4 =0, 4=a−4, a=8, If an = 0 ,, an = a + (n − 1) d, 0 = 8 + (n − 1) (−2) = 8 − 2n + 2, 2n = 10, n=5, So, the 5th term is 0, 10. The 17th term of an AP exceeds its 10th term by 7. Find the common difference., Solution:an = a + (n − 1) d, a = a + (17 − 1) d, a = a + 16d, Similarlly, a = a + 9d, But , a − a = 7, (a + 16d) − (a + 9d) = 7, 7d = 7, d=1, 11. Which term of the AP: 3, 15, 27, 39, . . . will be 132 more than its 54th term?, Solution:AP: 3, 15, 27, 39, …, a = 3,, d = a − a = 15 − 3 = 12, a = a + (54 − 1) d, a = 3 + (53) (12), a = 3 + 636 = 639, 132 + 639 = 771, Now we find which term is 771, a = 771., an = a + (n − 1) d, 771 = 3 + (n − 1) 12, 768 = (n − 1) 12, (n − 1) = 64, n = 65, There fore 65th term is 132 more than 54th term., Or, n’th term is 132 more than 54th term., n = 54 +, = 54 + 11 = 65th term., , P a g e 14 | 159 Available in ykoyyur.blogspot.com

Page 16 :
SSLC Mathematics Solutions – Part -1, , YK, , 12. Two APs have the same common difference. The difference between their 100th terms is, , 100, what is the difference between their 1000th terms?, Solution:Let the first terms of an AP’s be a’ and b’. Common difference – d, For the first AP,, a, = a + (100 − 1) d, a, = a + 99d, a, = a + (1000 − 1) d, a, = a + 999d, For 2 nd AP,, a, = b + (100 − 1) d, a, = b + 99d, a, = b + (1000 − 1) d, a, = b+ 999d, The difference of 100th terms is 100, There for (a + 99d) − (b + 99d) = 100, a − b = 100 ------------------- (i), The difference of 1000th terms is ?, (a + 999d) − (b + 999d) = a − b, From equation (i) ,, a1 − a2 = 100, So, the difference of 1000th terms is 100., 13. How many three-digit numbers are divisible by 7?, Solution:The first 3 digit number which is divisible by 7 is a = 105 and d = 7, The last 3 digit number which is divisible by 7 is, = 994, There for AP: 105, 112, 119, …994, n=?, an = a + (n − 1) d, 994 = 105 + (n − 1) 7, 889 = (n − 1) 7, (n − 1) = 127, n = 128, There for 128 three digit numbers are divisible by 7., Or, The 3-digit numbers which are divisible by 7 are 105, 112, 119, .... 994 ., These numbers are in AP:, a = 105 and d = 7, an = 994, ⇒ a + (n - 1) d = 994, ⇒ 105 + (n - 1) × 7 = 994, ⇒7(n - 1) = 889, ⇒ n - 1 = 127, ⇒ n = 128, 14. How many multiples of 4 lie between 10 and 250?, Solution:Multiples of 4 lie between 10 and 250 are 12, 16, 20, 24, …248, a = 12, d = 4, a = 248, an = a + (n - 1) d, , P a g e 15 | 159 Available in ykoyyur.blogspot.com

Page 17 :
SSLC Mathematics Solutions – Part -1, , YK, , 248 = 12 + (n - 1) × 4, 248 = 12 + 4n – 4, 248 = 8 + 4n, 4n = 248 - 8, 4n = 240, n = 60, Hence, ther are 60 multiples of 4 lie between 10 and 250., 15. For what value of n, are the nth terms of two APs: 63, 65, 67 , . . . and 3, 10, 17, . . . equal?, Solution: a = 63, d = a − a = 65 − 63 = 2, an = a + (n − 1) d, an = 63 + (n − 1) 2 = 63 + 2n − 2, an = 61 + 2n ----------- (i), 3, 10, 17, …, a = 3, d = a − a = 10 − 3 = 7, an = 3 + (n − 1) 7, an = 3 + 7n – 7, an = 7n − 4 ------------ (ii), According to question , nth term of both AP’s are equal., ⇒61 + 2n = 7n − 4, ⇒61 + 4 = 5n ⇒5n = 65, ⇒ n = 13, Hence, the 13th the two given AP’s are equal., 16. Determine the AP whose third term is 16 and the 7th term exceeds the 5th term by 12., a = 16, a + (3 − 1) d = 16, a + 2d = 16 ---------- (i), a − a = 12, [a+ (7 − 1) d] − [a + (5 − 1) d]= 12, (a + 6d) − (a + 4d) = 12, 2d = 12, d=6, From equation (i) ,, a + 2 (6) = 16, a + 12 = 16, a=4, Then the required AP is 4, 10, 16, 22, …, 17. Find the 20th term from the last term of the AP: 3, 8, 13, . . ., 253., Given AP: 3, 8, 13, …, 253, nth term from the last = l – ( n – 1)d, l = 253, a = 3, d = 5, nth term from the last = 253 – ( 20 – 1)5, = 253 – ( 19)5, = 253 – 95, = 253 – 95 = 158, 18. The sum of the 4th and 8th terms of an AP is 24 and the sum of the 6th and 10th terms is, 44. Find the first three terms of the AP., , P a g e 16 | 159 Available in ykoyyur.blogspot.com

Page 18 :
SSLC Mathematics Solutions – Part -1, , YK, , an = a + (n − 1) d, a = a + (4 − 1) d, a = a + 3d, Similarlly,, a = a + 7d, a = a + 5d, a = a + 9d, But , a + a = 24, a + 3d + a + 7d = 24, 2a + 10d = 24, a + 5d = 12 ------------(i), a + a = 44, a + 5d + a + 910d = 44, 2a + 14d = 44, a + 7d = 22 -----------(ii), By substracting (ii) from (i),, 2d = 22 − 12, 2d = 10, d=5, Substituting d = 5 in equation (i) ,, a + 5d = 12, a + 5 (5) = 12, a + 25 = 12, a = −13, a2 = a + d = − 13 + 5 = −8, a3 = a2 + d = − 8 + 5 = −3, Hence the first three terms are −13, −8, and −3., 19. Subbia Rao started work in 1995 at an annual salary of Rs 5000 and received an, increment of Rs 200 each year. In which year did his income reach Rs 7000?, The annual salary received by Subba Rao in the years 1995 onwards are, 5000, 5200, 5400,----7000, Hence, these numbers forms an AP., a = 5000, d = 200, an = 7000., an = a + (n − 1) d, 7000 = 5000 + (n − 1) 200, 200(n − 1) = 2000, (n − 1) = 10, n = 11, Thus the 11th years of his service or in 2005, Subba Rao received an annual salary of, Rs 7000., 20. Ramkali saved Rs 5 in the first week of a year and then increased her weekly savings, by Rs 1.75. If in the nth week, her weekly savings become Rs 20.75, find n., a = 5, d = 1.75, an = 20.75, n = ?, an = a + (n − 1) d, 20.75 = 5 + (n - 1) × 1.75, P a g e 17 | 159 Available in ykoyyur.blogspot.com

Page 19 :
SSLC Mathematics Solutions – Part -1, , YK, , 15.75 = (n - 1) × 1.75, 15.75 = 1.75n – 1.75, 1.75n = 15.75 + 1.75, 1.75n = 17.50, ., n=, =, = 10, ., , 1.4, , Sum of First n Terms of an AP, , • First term - a Common, difference - d, , • When the first and the last terms of an, AP are given and the common, difference is not given, , S = [2a + (n - 1)d], , S = [a + l], , Example 11 : Find the sum of the first 22 terms of the AP : 8, 3, –2, . . ., Solution: Here a = 8, d = 3 - 8 = -5, n = 22., S = [2a + (n - 1)d], S = [2x8 + (22 - 1)(-5)], S = 11[16 + 21(-5)], S = 11[16 - 105], S = 11x-89 = -979, Example 12 : If the sum of the first 14 terms of an AP is 1050 and its first term is 10,, find the 20th term., Solution: Here, S14 = 1050, n = 14, a = 10, S = [2a + (n - 1)d], 1050 =, , [2x10 + (14 - 1)d], , 1050 = 7[20 + 13d], 1050 = 140 + 91d, 91d = 1050 − 140, 91d = 910, d=, = 10, an = a + (n − 1) d, a = 10 + (20 – 1)10, a = 10 + 19x10, a = 10 + 190, a = 200, Example 13 : How many terms of the AP : 24, 21, 18, . . . must be taken so that their, sum is 78?, Solution:a = 24, d = 21-24 = -3, Sn = 78 , We have to find ‘n’, S = [2a + (n - 1)d], P a g e 18 | 159 Available in ykoyyur.blogspot.com

Page 20 :
SSLC Mathematics Solutions – Part -1, , YK, , 78 = [2x24 + (n - 1)(-3)], 78 = [48 - 3n + 3 ], 156 = [48 - 3n + 3 ], 156 = 51n - 3n2, 52 = 17n - n2, n2 – 17n + 52 = 0, n2 – 13n – 4n + 52 = 0, n(n – 13) – 4(n – 13) = 0, (n – 13) (n – 4) = 0, n = 13 CxÀªÁ n = 4, Example 14 : Find the sum of :, (i) the first 1000 positive integers (ii) the first n positive integers, Solution: (i) Let S = 1 + 2 + 3 +...... + 1000, S = [2a + (n - 1)d], S = 500[2 + 999], S = 500[1001], S = 500500, (i) Let S = 1 + 2 + 3 +...... + n, S = [2a + (n - 1)d], S = [2x1 + (n - 1)1], S = [2 + n - 1], S = [n + 1], Example 15 : Find the sum of first 24 terms of the list of numbers whose nth term is, given by an = 3 + 2n., Solution: an = 3 + 2n, a = 3 + 2x1 = 3 + 2 = 5, a = 3 + 2x2 = 3 + 4 = 7, a = 3 + 2x3 = 3 + 6 = 9, There for AP is : 5, 7, 9, - - a = 5, d = 2, n = 24, S = [2a + (n - 1)d], S=, , [2x5 + (24 - 1)2], , S = 12[10 + 23x2], S = 12[10 + 46], S = 12x56, S = 672, Example 16 : A manufacturer of TV sets produced 600 sets in the third year and 700 sets, in the seventh year. Assuming that the production increases uniformly by a fixed number, every year, find :, (i) the production in the 1st year, , (ii) the production in the 10th year, , (iii) the total production in first 7 years, P a g e 19 | 159 Available in ykoyyur.blogspot.com

Page 21 :
SSLC Mathematics Solutions – Part -1, , YK, , Solution:i) Since the production increases uniformly by a fixed number every year, the, number of TV sets manufactured in 1st, 2nd, 3rd, . . ., years will form an AP., Let us denote the number of TV sets manufactured in the nth year by an, a = 600, a = 700,, a + 2d = 600, a + 6d = 700, By solving the equation we get,, d = 25 and a = 550, (i) Therefore, production of TV sets in the first year is = 550, (ii) Production of TV sets in the 10th year is : a = a + 9d, a = 550 + 9x25, = 550 + 225 = 775, (iii) The total production of TV sets in first 7 years is, S = [2a + (n - 1)d], S = [2x550 + (7 - 1)25], S = [1100 + 6x25], S = [1100 + 150], S = [1250], S = 7x625 = 4375, , Exercise 1.3, 1. Find the sum of the following APs:, i) 2, 7, 12 ...... to 10 terms, a = 2, d =, − = 7 − 2 = 5, n = 10, Sn = [2a + (n - 1) d], , S10 = [2(2) + (10 - 1) × 5], S10 = 5[4 + (9) × (5)], S10 = 5 × 49 = 245, ii) -37, -33, -29 ...... to 12 terms, a = −37, d=, − = (−33) − (−37 = − 33 + 37 = 4, n = 12, Sn = [2a + (n - 1) d], S12 = [2(-37) + (12 - 1) × 4], S12 = 6[-74 + 11 × 4], S12 = 6[-74 + 44], S12 = 6(-30) = -180, iii) 0.6, 1.7, 2.5 ..... to 100 terms, a = 0.6, d = a2 − a1 = 1.7 − 0.6 = 1.1, n = 100, Sn = [2a + (n - 1) d], S100 =, , [1.2 + (99) × 1.1], , P a g e 20 | 159 Available in ykoyyur.blogspot.com

Page 22 :
SSLC Mathematics Solutions – Part -1, S100 = 50[1.2 + 108.9], S100 = 50[110.1], S100 = 5505, iv) , ,, ---------- to 11 terms, a=, d = a2 − a1 = − =, n = 11, Sn = [2a + (n - 1) d], , =, , S11 =, , [2x + (11 – 1 ) × ], , S11 =, , [ +, , S11 =, , [, , S11 =, , [ ], , ], ], , S11 = [ ] =, 2. Find the sums given below :, i) 7 + 10 + 14 + -------- + 84, a = 7, l = 84, d = a2 − a1 = 10 - 7 = - 7 =, l = a + (n - 1)d, 84 = 7 + (n - 1) ×, 77 = (n - 1) ×, 154 = 7n − 7, 7n = 161, n = 23, Sn = (a + l), S23 =, =, , (7 + 84), , x 91 =, , = 1046, ii) 34 + 32 + 30 + ...... + 10, a = 34, d = a2 − a1 = 32 − 34 = −2, l = 10, l = a + (n − 1) d, 10 = 34 + (n − 1) (−2), −24 = (n − 1) (−2), 12 = n − 1, n = 13, Sn = (a + l), S13 =, , (34 + 10), , S13 = x44, S13 = 13 × 22, S13 = 286, iii) -5 + (-8) + (-11)+ .... + (-230), a = −5, l = −230, d = a2 − a1 = (−8) − (−5) = − 8 + 5 = −3, l = a + (n − 1)d, P a g e 21 | 159 Available in ykoyyur.blogspot.com, , YK

Page 23 :
SSLC Mathematics Solutions – Part -1, −230 = − 5 + (n − 1) (−3), −225 = (n − 1) (−3), (n − 1) = 75, n = 76, Sn = (a + l), S76 = [(-5) + (-230)], S76 = 38(-235), S76 = -8930, 3. In an AP:, i) Given a = 5, d = 3, a n = 50 find n and Sn, a = 5, d = 3, an = 50, an = a + (n − 1)d,, ⇒ 50 = 5 + (n - 1) × 3, ⇒ 3(n - 1) = 45, ⇒ n - 1 = 15, ⇒ n = 16, Sn = (a + an), S16 = (5 + 50) = 440, S16 = 8 (55) = 440, ii) Given a = 7,, = 35 find d and S13, a = 7,, = 35, an = a + (n − 1)d,, ⇒ 35 = 7 + (13 - 1)d, ⇒ 12d = 28, ⇒ d = 28/12 = 2.33, Sn = (a + an), S13 =, , (7 + 35), , S13 = (42) = 13x21, S13 = 273, iii) Given, = 37, d = 3 find É a and S12, = 37, d = 3, an = a + (n − 1)d,, ⇒, = a + (12 − 1)3, ⇒ 37 = a + 33, ⇒a=4, Sn = (a + an), S12 = (4 + 37), S12 = 6 (41), S12 = 246, iv) Given, = 15, S10 = 125 findÉ d and, a3 = 15, S10 = 125, an = a + (n − 1)d,, a3 = a + (3 − 1)d, 15 = a + 2d ------------ (i), Sn = [2a + (n - 1) d], P a g e 22 | 159 Available in ykoyyur.blogspot.com, , YK

Page 25 :
SSLC Mathematics Solutions – Part -1, a = 8, an = 62, Sn = 210, Sn = (a + an), 210 = (8 + 62), ⇒ 35n = 210, ⇒ n=, =6, = a + (n – 1)d, 62 = 8 + 5d, ⇒ 5d = 62 - 8 = 54, ⇒ d = = 10.8, viii) Given an = 4, d = 2, Sn = -14 findÉ n and a, an = 4, d = 2, Sn = −14, an = a + (n − 1)d, 4 = a + (n − 1)2, 4 = a + 2n − 2, a + 2n = 6, a = 6 − 2n ---------- (i), Sn = (a + an), -14 = (a + 4), −28 = n (a + 4), −28 = n (6 − 2n + 4) {From equation (i)À}, −28 = n (− 2n + 10), −28 = − 2n2 + 10n, 2n2 − 10n − 28 = 0, n2 − 5n −14 = 0, n2 − 7n + 2n − 14 = 0, n (n − 7) + 2(n − 7) = 0, (n − 7) (n + 2) = 0, Either n − 7 = 0 or n + 2 = 0, n = 7 or n = −2, From equation (i) ,, a = 6 − 2n, a = 6 − 2(7), a = 6 − 14, a = −8, ix) Given a = 3, n = 8, S = 192 find d, a = 3, n = 8, S = 192, Sn = [2a + (n - 1)d], 192 = [2 × 3 + (8 - 1)d], 192 = 4 [6 + 7d], 48 = 6 + 7d, 42 = 7d, d=6, x) Given l = 28, S = 144 and there are 9 terms. Find the value of a, l = 28, S = 144, n = 9, Sn = (a + l), P a g e 24 | 159 Available in ykoyyur.blogspot.com, , YK

Page 26 :
SSLC Mathematics Solutions – Part -1, , YK, , 144 = (a + 28), (16) × (2) = a + 28, 32 = a + 28, a=4, 4. How many terms of the AP : 9, 17, 25, . . . must be taken to give a sum of 636?, a=9, d = a2 − a1 = 17 − 9 = 8, Sn = [2a + (n - 1)d], 636 = [2 × a + (8 - 1) × 8], 636 = [18 + (n- 1) × 8], 636 = n [9 + 4n − 4], 636 = n (4n + 5), 4n2 + 5n − 636 = 0, 4n2 + 53n − 48n − 636 = 0, n (4n + 53) − 12 (4n + 53) = 0, (4n + 53) (n − 12) = 0, 4n + 53 = 0 or n − 12 = 0, n = (-53/4) or n = 12, ⇒n = 12, 5. The first term of an AP is 5, the last term is 45 and the sum is 400. Find the number of terms, and the common difference., a = 5, l = 45, Sn = 400, Sn = (a + l), 400 = (5 + 45), 400 = (50), 25n = 400, n = 16, l = a + (n − 1) d, 45 = 5 + (16 − 1) d, 40 = 15d, d= =, 6. The first and the last terms of an AP are 17 and 350 respectively. If the common difference, is 9, how many terms are there and what is their sum?, a = 17, l = 350, d = 9, l = a + (n − 1) d, 350 = 17 + (n − 1)9, 333 = (n − 1)9, (n − 1) = 37, Sn = (a + l), S38 = (17 + 350), S38 = 19 × 367, S38 = 6973, 7. Find the sum of first 22 terms of an AP in which d = 7 and 22nd term is 149., d = 7,, = 149, S22 = ?, an = a + (n − 1)d, a22 = a + (22 − 1)d, P a g e 25 | 159 Available in ykoyyur.blogspot.com

Page 27 :
SSLC Mathematics Solutions – Part -1, , YK, , 149 = a + 21 × 7, 149 = a + 147, a=2, Sn = (a + an), S22 = (2 + 149) = 11 × 151, S22 = 1661, 8. Find the sum of first 51 terms of an AP whose second and third terms are 14 and 18, respectively., a2 = 14, a3 = 18, d = a3 − a2 = 18 − 14 = 4, a2 = a + d, 14 = a + 4, a = 10, Sn = [2a + (n - 1)d], S51 =, , [2 × 10 + (51 - 1) × 4], , =, , [20 + (50) × 4], , =, , [20 + 200], , = [220] = 51 × 110 = 5610, 9. If the sum of first 7 terms of an AP is 49 and that of 17 terms is 289, find the sum of, first n terms., S7 = 49, S17 = 289, Sn = [2a + (n - 1)d], S7 =, , [2a + (n - 1)d], , S7 = [2a + (7 - 1)d], 49 = [2a + 6d], 7 = (a + 3d), a + 3d = 7 ----------- (i), Similarlly,, S17 =, 289 =, , [2a + (17 - 1)d], (2a + 16d), , 17 = (a + 8d), a + 8d = 17 --------- (ii), Substract equation (ii) from (i), 5d = 10 ⇒ d = 2, From equation (i), a + 3(2) = 7, a+6=7 ⇒a=1, Sn = [2a + (n - 1)d], = [2(1) + (n - 1) × 2] = (2 + 2n - 2), = (2n) = n2, , P a g e 26 | 159 Available in ykoyyur.blogspot.com

Page 28 :
SSLC Mathematics Solutions – Part -1, , YK, , 10. Show that a1, a2, a3 ..... a n ,......form an AP where a n is defined as below, (i) = 3 + 4n (ii) = 9 - 5n, Also, find the sum of the first 15 terms in each case., (i) = 3 + 4n, a1 = 3 + 4(1) = 7, a2 = 3 + 4(2) = 3 + 8 = 11, a3 = 3 + 4(3) = 3 + 12 = 15, a4 = 3 + 4(4) = 3 + 16 = 19, ⇒ a2 − a1 = 11 − 7 = 4, a3 − a2 = 15 − 11 = 4, a4 − a3 = 19 − 15 = 4, So, the given sequence forms an AP with first term =7 and common difference = 4, Sn = [2a + (n - 1)d], , S15 =, =, , [2(7) + (15 - 1) × 4], , [(14) + 56], , = (70) = 15 × 35 = 525, (ii) = 9 - 5n, a1 = 9 − 5 × 1 = 9 − 5 = 4, a2 = 9 − 5 × 2 = 9 − 10 = −1, a3 = 9 − 5 × 3 = 9 − 15 = −6, a4 = 9 − 5 × 4 = 9 − 20 = −11, ⇒ a2 − a1 = − 1 − 4 = −5, a3 − a2 = − 6 − (−1) = −5, a4 − a3 = − 11 − (−6) = −5, So, the given sequence forms an AP with first term = 4 and common difference = -5, Sn = [2a + (n - 1)d], S15 =, , [2(4) + (15 - 1) (-5)], , =, , [8 + 14(-5)], , =, , (8 - 70) =, , (-62) = 15(-31) = -465, , 11. If the sum of the first n terms of an AP is 4n – n2, what is the first term (that is S )? What, is the sum of first two terms? What is the second term? Similarly, find the 3rd, the 10th and, the nth terms., Sn = 4n − n2, First term a = S1 = 4(1) − (1) 2 = 4 − 1 = 3, Sum of first two terms, S2= 4(2) − (2)2 = 8 − 4 = 4, a2 = S2 − S1 = 4 − 3 = 1, d = a2 − a = 1 − 3 = −2, nth term an = a + (n − 1)d, = 3 + (n − 1) (−2), = 3 − 2n + 2, = 5 − 2n, So, the third term a3 = 5 − 2(3) = 5 − 6 = −1, 10th term a10 = 5 − 2(10) = 5 − 20 = −15, , P a g e 27 | 159 Available in ykoyyur.blogspot.com

Page 29 :
SSLC Mathematics Solutions – Part -1, , YK, , 12. Find the sum of the first 40 positive integers divisible by 6., 6, 12, 18, 24 …, This is an AP with common difference = 6 and the first term = 6, a = 6, d = 6, S40 = ?, Sn = [2a + (n - 1)d], , S40 =, , [2(6) + (40 - 1) 6], , = 20[12 + (39) (6)], = 20(12 + 234) = 20 × 246 = 4920, 13. Find the sum of the first 15 multiples of 8., The numbers multiples of 8 are, 8, 16, 24, 32…, These numbers form an AP with common difference 8 and the first term 8, a = 8, d = 8, S15 = ?, Sn = [2a + (n - 1)d], S15 =, =, , [2(8) + (15 - 1)8], , [6 + (14) (8)], , = [16 + 112] = (128) = 15 × 64 = 960, 14. Find the sum of the odd numbers between 0 and 50., The odd numbers between 0 and 50, 1, 3, 5, 7, 9 … 49, This is an AP with common difference 1 and the first term 2, a = 1, d = 2, l = 49, l = a + (n − 1) d, 49 = 1 + (n − 1)2, 48 = 2(n − 1), n − 1 = 24, n = 25, Sn = (a + l), S25 =, , (1 + 49), , =, (50) = (25)(25) = 625, 15. A contract on construction job specifies a penalty for delay of completion beyond a, certain date as follows: Rs 200 for the first day, Rs 250 for the second day, Rs 300 for the, third day, etc., the penalty for each succeeding day being Rs 50 more than for the, preceding day. How much money the contractor has to pay as penalty, if he has delayed, the work by 30 days?, This is an AP with common difference 50 and the first term 200, a = 200, d = 50, The penalty payable for the delay of 30 days = S30, Sn = [2a + (n - 1)d], S30 =, [2(200) + (30 - 1) 50], = 15 [400 + 1450] = 15 (1850), = Rs 27750, , P a g e 28 | 159 Available in ykoyyur.blogspot.com

Page 30 :
SSLC Mathematics Solutions – Part -1, , YK, , 16. A sum of Rs 700 is to be used to give seven cash prizes to students of a school for their, overall academic performance. If each prize is Rs 20 less than its preceding prize, find the, value of each of the prizes., Let the first prize = a, The amount of 2nd prize = a − 20, The amount of 3rd prize = a − 40, This is an AP with common difference -20 and the first term a, d = −20, S7 = 700, Sn = [2a + (n - 1)d], , [2a + (7 - 1)d] = 700, [2a + 6d] = 700, 7 [a + 3d] = 700, a + 3d = 100, a + 3(−20) = 100, a − 60 = 100, a = 160, So, the values of prizes Rs 160, Rs 140, Rs 120, Rs 100, Rs 80, Rs 60, and Rs 40., 17. In a school, students thought of planting trees in and around the school to reduce air, pollution. It was decided that the number of trees, that each section of each class will, plant, will be the same as the class, in which they are studying, e.g., a section of Class I, will plant 1 tree, a section of Class II will plant 2 trees and so on till Class XII. There are, three sections of each class. How many trees will be planted by the students?, 1, 2, 3, 4, 5………………..12, This is an AP with common difference 1 and the first term 1, a = 1, d = 2 − 1 = 1, Sn = [2a + (n - 1)d], S12 = [2(1) + (12 - 1)(1)], = 6 (2 + 11) = 6 (13) = 78, Hence, the trees planted by the students of each section = 78, There for the trees planted by the students of 3 sections = 78 x 3 = 234, 18. A spiral is made up of successive semicircles, with centres alternately at A and B,, starting with centre at A, of radii 0.5 cm, 1.0 cm, 1.5 cm, 2.0 cm, . . . as shown in Fig., 1.4. What is the total length of such a spiral made up of thirteen consecutive semi, circles (Take π = ), , [Hint: length of successive semi circles is l1, l2, l3, l4, .....with centers as A, B,A,B ..... l1, l2, l3, l4, .....], , P a g e 29 | 159 Available in ykoyyur.blogspot.com

Page 31 :
SSLC Mathematics Solutions – Part -1, , YK, , The length of the semi circles = πr, l1 = π(0.5) = cm, l2 = π(1) = π cm, l3 = π(1.5) = cm, l1, l2, l3 . . . are the lengths of semicircles, , π, , 2π, ...., d = l2- l1 = π - =, a = cm, Sn = [2a + (n - 1)d], There for the total length of such a spiral made up of thirteen consecutive semi circles, S13 = [2x + (13 - 1) ] =, [π + 6π], =, , (7π) =, , ×7×, , = 143 cm, , 19. 200 logs are stacked in the following manner: 20 logs in the bottom row, 19 in the next row,, , 18 in the row next to it and so on (see Fig. 1.5). In how many rows are the 200 logs placed, and how many logs are in the top row?, , The logs are in an AP, 20, 19, 18…, a = 20, d = a2 − a1 = 19 − 20 = −1, Sn = 200, Sn = [2a + (n - 1)d], 200 = [2(20) + (n - 1)(-1)], 200 = [40 - n + 1], 400 = n (40 − n + 1), 400 = n (41 − n), 400 = 41n − n2, n2 − 41n + 400 = 0, n2 − 16n − 25n + 400 = 0, n (n − 16) −25 (n − 16) = 0, (n − 16) (n − 25) = 0, (n − 16) = 0 or n − 25 = 0, n = 16 or n = 25, an = a + (n − 1)d, a16 = 20 + (16 − 1) (−1)⇒ a16 = 20 − 15 = 5, Similarly,, a25 = 20 + (25 − 1) (−1) = 20 − 24, = −4 (negetive number is not possible), Hence the number of rows is 16 and the number of logs in the top row is 5, P a g e 30 | 159 Available in ykoyyur.blogspot.com

Page 32 :
SSLC Mathematics Solutions – Part -1, , YK, , 20. In a potato race, a bucket is placed at the starting point, which is 5 m from the first potato,, and the other potatoes are placed 3 m apart in a straight line. There are ten potatoes in the, line (see Fig. 1.6)., , A competitor starts from the bucket, picks up the nearest potato, runs back with it, drops, it in the bucket, runs back to pick up the next potato, runs to the bucket to drop it in, and, she continues in the same way until all the potatoes are in the bucket. What is the total, distance the competitor has to run?, [Hint : To pick up the first potato and the second potato, the total distance (in metres), run by a competitor is 2 × 5 + 2 × (5 + 3)], The distances from the bucket to potatos 5, 8, 11, 14…, They have to run twice, then the distacnes run by the competiror 10, 16, 22, 28, 34,………., a = 10, d = 16 − 10 = 6, S10 =?, Sn = [2a + (n - 1)d], S10 =, , [2(10) + (10 - 1)(6)], , = 5[20 + 54] = 5 (74) = 370, Hence, the distance the competitor has to run is 370km, , Summery:, , , , An arithmetic progression (AP) is a list of numbers in which each term is obtained, by adding a fixed number d to the preceding term, except the first term. The fixed, number d is called the common difference, , , , , The general form of an AP : a, a + d, a + 2d, a + 3d......, , , , The AP has infinite number of terms is called infinite Arithmetic, Progression. Such APs do not have a last term., , , , The first term – a and the common difference is d then the nth term of, an AP, = + ( − 1), , , , The nth term from the last [ last term – l , common difference – d ], − ( − 1), , , , a is the first term, d is the common difference then sum to nth term, S = [2a + (n - 1)d], , , , If common difference is unknown then the sum to nth term, S = [a + l] { l – the last term }, , In an AP if there are only a finite number of terms. Such an AP is called, a finite AP. Such AP has a last term., , P a g e 31 | 159 Available in ykoyyur.blogspot.com

Page 33 :
SSLC Mathematics Solutions – Part -1, , YK, , Triangles, 2.2 Similar Figures, Two polygons of the same number of sides are similar, if, All the corresponding angles are equal and, , All the corresponding sides are in the same ratio (or, proportion)., , EXERCISE 2.1, 1., , Fill in the blanks using the correct word given in brackets, i) All circles are _____________ (congruent, similar), ii) All squares are ____________(similar, congruent), iii) All____________triangles are similar. (isosceles, equilateral), iv) Two polygons of the same number of sides are similar, if (a) their corresponding angles, are___________and (b) their corresponding sides are____________(equal, proportional), , 2., , Give two different examples of pair of, , 3., , (i) similar figures., (ii) non-similar figures., State whether the following quadrilaterals are similar or not:, , Solutions:, 1. Fill in the blanks using the correct word given in brackets, v) All circles are similar (congruent, similar), vi) All squares are similar (similar, congruent), vii) All similar triangles are equilateral. (isosceles, equilateral), viii) Two polygons of the same number of sides are similar, if (a) their corresponding, angles are equal and (b) their corresponding sides are proportional (equal,, proportional), , P a g e 32 | 159 Available in ykoyyur.blogspot.com

Page 34 :
SSLC Mathematics Solutions – Part -1, , YK, , 1. Give two different examples of pair of, (i) similar figures:, Pair of circles, Pair of squares, (ii) non-similar figures., A triangle and a square, 4., , A rectangle and a Quadrilateral, State whether the following quadrilaterals are similar or not:, , The corresponding angles are not equal. Hence, they are not similar, , 2.3 Similarity of Triangles, Basic proportionality theorem[Thales theorem], , If a line is drawn parallel to one side of a triangle to, intersect the other two sides in distinct points, the other two, sides are divided in the same ratio, , Data: In ∆ABC, the line drawn parallel to BC intersects AB and AC at D and E ., To prove:, , =, , ,, , Construction: Join BE and CD. Draw DM⟘AC and EN⟘AB., , P a g e 33 | 159 Available in ykoyyur.blogspot.com

Page 35 :
SSLC Mathematics Solutions – Part -1, , YK, , Proof :, (∆, , ), , (∆, , ), , (∆, , ), , (∆, , ), , =, , =, , ×, , ×, , ×, , ×, , ×, , ×, , ×, , ×, , =, , [ ∵Area of triangle =, , x Base x Height], , =, , ∆BDE and ∆DEC stand on the same base DE and in between BCǁDE, ∴ Area (∆BDE) = Area (∆DEC), --- (3), ∴ From (1), (2) and (3),, , =, , If a line divides any two sides of a triangle in the same, ratio, then the line is parallel to the third side., , Example 1 :If a line intersects sides AB and AC of a ABC at D and E respectively and is parallel, to BC, prove that, , =, , ( See fig 2.13 ), , Solution: DEǁBC (Data), ∴, , =, , or, , =, , +1 =, , ( Theorem 2.1), , +1, , =, =, , (∵ Taken reciprocals), , Example 2 : ABCD is a trapezium with AB || DC. E and F are points on non parallel sides AD, a n d BC r es pect ively su ch tha t EF is parallel to (See fig 2.14 ) Show that, , solution: Join AC to intersect EF at G. (See fig 2.15), ABǁDC ªÀÄvÀÄÛ EFǁAB (Given), So,, , EF || DC (Lines parallel to the same line are parallel to each other ), , P a g e 34 | 159 Available in ykoyyur.blogspot.com, , =

Page 36 :
SSLC Mathematics Solutions – Part -1, , YK, , Now in ∆ADC,, EGǁDC (∵EFǁDC), , =, , ∴, , (Theorem 2.1) ----(1), , Similarly, from ∆CAB,, , =, =, , i.e.,, , ----(2), , ∴ From (1), (2) axiom (1),, , =, Example 3 : In Fig. 2.16,, triangle., Solution:, Given that,, , =, , and ∠PST = ∠PRQ prove that ∆PQR is an isosceles, , =, , ∴ STǁQR (∵Theorem 2.2), ⇒∠PST = ∠PQR (∵Corresponding angles) ----(1), But, ∠PST = ∠PRQ (∵ Given ), -------(2), So, ∠PRQ = ∠PQR [from (1), (2) and axiom (1) ], Therefore, PQ = PR (∵Sides opposite the equal angles), i.e., PQR is an isosceles triangle., , Exercise 2.2, 1. In Fig. 2.17, (i) and (ii), DE || BC. Find EC in (i) and AD in (ii)., , (i) In triangle△ABC, DE∥BC (Given), , ∴, ⇒, , =, ., , [Thales theorem], , =, , ⇒ EC =, , ., , =, , = 2 cm., , (ii) In △ABC, DE∥BC (Given), , ∴, ⇒, , =, ., , =, , [Thales theorem], ., ., , P a g e 35 | 159 Available in ykoyyur.blogspot.com

Page 37 :
SSLC Mathematics Solutions – Part -1, ., , ⇒ AD =, , ., , ., , =, , ., , YK, , = 2.4 cm., , 2. E and F are poin ts on th e sides PQ an d PR respectively of a PQR. For each of, the following cases, state whether EF || QR :, (i) PE = 3.9cm EQ = 3cm PF = 3.6cm FR = 2.4cm, (ii) PE = 4cm QE = 4.5cm PF = 8cm RF = 9cm, (iii) PQ = 1.28cm PR = 2.56cm PE = 0.18cm PF = 0.36cm, Solution:, (i) PE = 3.9 cm, EQ = 3 cm ,PF = 3.6 cm, FR = 2,4 cm (Given), ., , =, , ∴, , =, ., , =, , And, , ., , = 1.3 [Thales theorem], , =, , Therefore ,, , = 1.5, , ≠, , Hence, EF is not parallel to QR, (ii) PE = 4 cm, QE = 4.5 cm, PF = 8cm, RF = 9cm, ∴, , =, , And,, , =, , ., , =, , [Thales theorem], , =, , Therefore ,, , =, , Hence, EFǁQR, (iii) PQ = 1.28 cm, PR = 2.56 cm, PE = 0.18 cm, PF = 0.36 cm, Here, EQ = PQ - PE = 1.28 - 0.18 = 1.10 cm, And, FR = PR - PF = 2.56 - 0.36 = 2.20 cm, ∴, , =, , and,, , ., , =, , ∴, , =, , ., ., ., , =, =, , ... (i), =, , ... (ii), , =, , There fore, EFǁQR, 3. In Fig. 2.18, if LM || CB and LN || CD, prove that, , =, In the given fig, LM || CB,, , =, , ... (i) [corollary of BPT], , Similarlly, LN || CD,, , =, , ∴, , ... (ii) [corollary of BPT], , From (i) and (ii) ,, =, 4. In Fig. 2.19, DE || AC and DF || AE. Prove that, , =, P a g e 36 | 159 Available in ykoyyur.blogspot.com

Page 38 :
SSLC Mathematics Solutions – Part -1, , YK, , In ΔABC, DE || AC (Given), , ∴, , =, , -------(1) [ Thales theorem], , In ΔABC, DF || AE (Given), , ∴, , =, , -----------(2) [ Thales theorem], , From equation (i) and (ii), =, 5. In Fig. 2.20, DE || OQ and DF || OR. Show that EF || QR, In ΔPQO, DE || OQ (Given), , ∴, , =, , -------------- (1) [ Thales theorem], , In ΔPOR, DF || OR (Given), , ∴, , =, , ⇒, , ---------------(2) [ Thales theorem], , [From equation (1) and (2) ], , =, , ∴ In ΔPQR, EF || QR. [Converse of BPT], 6. In Fig. 2.21, A, B and C are points on OP, OQ and OR respectively such that AB || PQ, and AC || PR. Show that BC || QR., In ΔOPQ, AB || PQ (Given), , ∴, , =, , -------------------(1) [ Thales theorem], , In ΔOPR, AC || PR (Given), , ∴, , =, , -------------------(2) [ Thales theorem], , [From equation (1) and (2) ], , =, , ∴ ΔOQR £À°è, BC || QR. [Converse of BPT], 7. Using Theorem 2.1, prove that a line drawn through the mid-point of one side of a triangle, parallel to another side bisects the third side. (Recall that you have proved it in Class, IX)., Data: : In ΔABC, D is the mid-point of AB ⇒ AD=DB., The parallel line DE to BC drawn from D intersects AC at E, To prove: E is the mid-point of AC., Proof: D is the mid-point of AB., ∴ AD = DB, , ⇒, , = 1, , ----------------------(1), , In ΔABC, DE || BC,, , ∴, , =, , [Thales theorem] ⇒1 =, , [From equation (1)], , ∴ AE =EC ⇒ E is the mid-point of AC, 8. Using Theorem 2.2, prove that the line joining the mid-points of any two sides of a, triangle is parallel to the third side. (Recall that you have done it in Class IX)., Data: In ΔABC, D and E are the mid-points of AB and AC, , P a g e 37 | 159 Available in ykoyyur.blogspot.com

Page 39 :
SSLC Mathematics Solutions – Part -1, , YK, , ⇒AD=BD and AE=EC., To prove: DE || BC, Proof: D is the mid-point of AB (Given), ∴ AD = DB ⇒, , = 1 ------------------------ (1), , E is the mid-point of AC (Given), ∴ AE=EC ⇒, , = 1 --------------------------(2), , [From equation (1) and (2)], , =, , ∴ DE || BC [By BPT], 9. ABCD is a trapezium in which AB || DC and its diagonals intersect each other at the point O., Show that, , =, , Data: In trapezium ABCD, ABǁBC, and AC and BD intersects each other at O., To Prove:, , =, , Construction: Draw EO from O such that EO || DC || AB, ProofÉ: In ΔADC, OE || DC (Construction), , =, , -------------------------(1) [By BPT], , In ΔABD, OE || AB (Construction), , =, , [By BPT], , =, , ⇒, , ----------------------(2) [ Taken reciprocals], , =, ⇒, , [From equation (1) and (2)], =, , 10. The diagonals of a quadrilateral ABCD intersect each other at the point O such, , =, , that, , Show that ABCD is a trapezium, , Given: In ABCD, AC and BD intersects at O, Such that, , =, , To prove: ABCD is a trapezium, Construction: Draw EO through O such that EO || AB which, Intersects AD at E, Proof: In ΔDAB, EO || AB, , ∴, , =, , Similarlly,, ⇒, , [ BPT] ⇒, , =, , =, , ------------------------- (1) [taken reciprocals], , (Given), , =, , -----------------(2), , ∴, , =, [From equation (1) and (2)], EO || DC ªÀÄvÀÄÛ EO || AB [ converse of BPT], , ⇒ AB || DC., ∴ABCD is a trapezium, P a g e 38 | 159 Available in ykoyyur.blogspot.com

Page 40 :
SSLC Mathematics Solutions – Part -1, , YK, , 2.4 Criteria for Similarity of Triangles, , It must be noted that as done in the case of congruency of two, triangles, the similarity of two triangles should also be expressed, symbolically, using correct correspondence of their vertices. For, example, for the triangles ABC and DEF of Fig. 2.22, we cannot write, ABC ~ EDF or ABC ~ FED. However, we can write BAC ~ EDF, If in two triangles, corresponding angles are equal, then their, corresponding sides are in the same ratio (or proportion) and, hence the two triangles are similar., , This criterion is referred to as the AAA (Angle–Angle–Angle) cr, it er ion of similarity of two triangles., , Data: In ∆ABC and ∆DEF,, ∠A = ∠D, ∠B = ∠E and ∠C = ∠F, To prove:, , =, , =, , (<1) and ∆ABC~ ∆DEF, , Construction:Cut DP = AB from DE and DQ = AC, from DF and join PQ, ProofÉ: In ∆ABC and ∆DPQ,, AB = DP, [Construction], AC = DQ, [Construction], ∠A = ∠D, [data], ∴∆ABC ≅ ∆DPQ [SAS Congruency rule], ⇒BC = PQ ---------(1) and, ⇒ ∠B = ∠P [CPCT] But ∠B = ∠E [Given], ∴ ∠P = ∠E, ∴PQǁEF [Since corresponding angles are equal], ∴, , =, , =, , [by Corolary of BPT], , P a g e 39 | 159 Available in ykoyyur.blogspot.com

Page 41 :
SSLC Mathematics Solutions – Part -1, =, , ⇒, , =, , YK, , [By construction and (1) ], , ∴∆ABC~ ∆DEF, , If two angles of one triangle are respectively equal to two angles of another, triangle, then the two triangles are similar., This may be referred to as the AA similarity criterion for two triangles., , If in two triangles, sides of one triangle are proportional to, (i.e., in the same ratio of ) the sides of the other triangle, then, their corresponding angles are equal and hence the two, triangles are similiar., This criterion is referred to as the SSS (Side–Side–Side) similarity criterion for two triangles., Data: In ∆ABC and ∆DEF,, , =, , =, , (<1) ---------(1), , To Prove: ∠A = ∠D, ∠B = ∠E and ∠C = ∠F, And ∆ABC ≅ ∆ DEF, Construction: Cut DP = AB from DE and, DQ = AC from DF.Join PQ, , =, , Proof :, ⇒, , =, , [Given], [∵ DP = AB, DQ = AC], , ∴ PQǁEF [corollary of Converse of BPT in ∆ DEF], ⇒ ∠P = ∠E ªÀÄvÀÄÛ ∠Q = ∠F, ∴ ∆DPQ ~∆DEF [ AA Similarity criteria], ∴, ⇒, , =, =, =, , But,, , ⇒, , [Corresponding sides of similar triangles], , =, , ------(1) [AB = DP Construction], -------(2) [Given], , [ ∵ (1) ªÀÄvÀÄÛ (2) jAzÀ], , ⇒BC = PQ, In ∆ABC and ∆DPQ ,, BC = PQ, [Proved], AB = DP, [Construction], AC = DQ, [Construction], ∴∆ABC ≅ ∆DPQ [SSS Congruency rule], Hence, ∠A = ∠D, ∠B = ∠P and ∠C = ∠Q, ⇒∠A = ∠D, ∠B = ∠E and ∠C = ∠F and ∆ABC ≅ ∆ DEF, P a g e 40 | 159 Available in ykoyyur.blogspot.com

Page 42 :
SSLC Mathematics Solutions – Part -1, , YK, , Theorem 2.5 : If one angle of a triangle is equal to one, angle of the other triangle and the sides including these, angles are proportional, then the two triangles are similar, , Given:In ∆ABC and ∆DEF, ∠A = ∠D and, , =, , (< 1) ------------ (1), , To Prove: ∆ABC ≅ ∆DEF, Construction: Cut DP = AB from DE, and DQ = AC from DF.Join PQ, Proof: In ∆ABC and ∆DPQ,, AB = PQ [By Construction], AC = DF [By Construction], ∠A = ∠D [Given], ∆ABC ≅ ∆DPQ [ By SAS Congruency rule]----------(2), From eqn (1) we get,, , ⇒, , =, , =, , [AB = DP and AC = DQ], , ⇒ PQǁEF [By converse of corollary of BPT], ⇒∠P = ∠E , ∠Q = ∠F [Corresponding angles], ∴ ∆DPQ ~ ∆DEF [by AA similarity ctriteria] --------(3), ⇒ ∆ABC ≅ ∆DEF [From equation (2) and (3) ], Example 4 : In Fig. 2.29, if PQ || RS, prove that ∆POQ ~ ∆SOR, Solution: PQǁRS [given], ∴ ∠P = ∠S, [Alternate angles], ∠Q = ∠R [Alternate angles], And ∠POQ = ∠SOR [vertically opposite angles], ∴∆POQ ~ ∆SOR [AAA similarity criteria], Example 5 : Observe Fig. 2.30 and then find P., Solution: In ∆ABC and ∆PQR,, , =, , ., ., , =, , And, ⇒, , = ,, , =, , √, √, , =, , =, , =, , =, , ∴ ∆ABC ~ ∆RQP [SSS similarity criteria], ∠C = ∠P [Corresponding angles of similar triangles], But ∠C = 180 - ∠A - ∠B [The sum of interior angles of a triangle is 180 0], =180 0 – 800 - 600 = 400 ⇒ ∠P = 400, , P a g e 41 | 159 Available in ykoyyur.blogspot.com

Page 43 :
SSLC Mathematics Solutions – Part -1, , YK, , Example 6 : In Fig. 2.31, OA . OB = OC . OD. Show that ∠A = ∠C ªÀÄvÀÄÛ ∠B = ∠D., Solution: OA.OB = OC.OD [Given], ⇒, , =, , ------ (1), , ∠AOD = ∠COB [Vertically opposite angles] -----(2), From equation (1) and (2),, ∆AOD ~ ∆COB [SAS similarity criteria], ∴ ∠A = ∠C and ∠D = ∠B [Corresponding angles of similar triangles], Example 7 : A girl of height 90 cm is wa lking a wa y fr om t he ba se of a lamppost at a speed of 1.2 m/s. If the lamp is 3.6 m above the ground, find the length of her, shadow after 4 seconds., Solution:, AB is a Lamp post. CD i the hs hight of the girl, DE is the length of the shadow of the girl., Let DE = x’ m, Now, BD = 1.2m × 4 = 4.8m, In ∆ABE and ∆CDE,, ∠B = ∠D = 90 0, And ∠E = ∠E [Common angle], ∴ ∆ABE ~ ∆CDE [AA similarity criteria], ∴, =, ⇒, , ., , =, , ., ., , ( ∵90cm =, , m = 0.9m), , ⇒ 4.8+x = 4x, ⇒ 3x = 4.8, ⇒x = 1.6, Hence, the length of her shadow after 4 seconds is 1.6m, Example 8 : In Fig. 2.33, CM and RN are r es pect ively th e media ns of, a nd ∆PQR. If ∆ABC ~ ∆PQR, prove that :, (i) ∆AMC ~ ∆PNR, (ii), =, iii) ∆CMB ~ ∆RNQ, Solution:, i) ∆ABC ~ ∆PQR, ⇒, , =, , =, , ---------(1), , and ∠A = ∠P , ∠B = ∠Q , ∠C = ∠R ------ (2), But, AB = 2AM and PQ = 2PN [CM and RN are the medians], ⇒, , =, , ⇒, , =, , ------------(3), , But, ∠A = ∠P [ From (2) ] ---------(4), P a g e 42 | 159 Available in ykoyyur.blogspot.com, , ∆ABC

Page 44 :
SSLC Mathematics Solutions – Part -1, From (3) and (4),, ∆AMC ~ ∆PNR [SAS similarity criteria], , =, , ii) From (5), , =, , But,, ∴, , --(5), , -------(6), , [From (1)] -------(7), , =, , -------(8), , =, , (iii), , YK, , ------ (9), , ⇒, , =, , [From (8)], , ⇒, , =, , =, , ⇒, , =, , ⇒, , =, , [CM and RN are the medians], ------- (10), , =, , [From (9) and (10)], , ∴ ∆CMB ~ ∆RNQ [SSS similarity criteria], [ Note: you can solve (ii) and (iii) using same method as solved for (i)], , Exercise 2.3, 1) State which pairs of triangles in Fig. 6.34 are similar. Write the similarity criterion used by, you for answering the question and also write the pairs of similar triangles in the symbolic, form :., , P a g e 43 | 159 Available in ykoyyur.blogspot.com

Page 45 :
SSLC Mathematics Solutions – Part -1, (i) In ΔABC and ΔPQR,, ∠A = ∠P = 60° [Given] ; ∠B = ∠Q = 80° [Given]; ∠C = ∠R = 40° [Given], ∴ ΔABC ~ ΔPQR [AAA similarity criteria], (ii) In ΔABC and ΔPQR ,, , =, , =, , ∴ ΔABC ~ ΔQRP [SSS similarity criteria], (iii)In ΔLMP and ΔDEF,, LM = 2.7, MP = 2, LP = 3, EF = 5, DE = 4, DF = 6, =, , =, , =, , =, , =, , ., , =, , Here,, , =, , ≠, , ∴ ΔLMP and ΔDEF are not similar, (iv) In ΔMNL and ΔQPR,, =, , =, , ∠M = ∠Q = 70°, ∴ ΔMNL ~ ΔQPR [SAS similarity criteria], (v) In ΔABC and ΔDEF,, AB = 2.5, BC = 3, ∠A = 80°, EF = 6, DF = 5, ∠F = 80°, ⇒, and,, , =, , ., , =, , = =, , ⇒ ∠B ≠ ∠F, ⇒ ΔABC and ΔDEF are not similar, (vi) In ΔDEF,, ∠D + ∠E + ∠F = 180° [Sum of the interior angles of a triangle], ⇒ 70° + 80° + ∠F = 180°, ⇒ ∠F = 180° - 70° - 80°, ⇒ ∠F = 30°, In ∆PQR,, ∠P + ∠Q + ∠R = 180 [Sum of the interior angles of a triangle], ⇒ ∠P + 80° + 30° = 180°, ⇒ ∠P = 180° - 80° -30°, ⇒ ∠P = 70°, In ΔDEF and ΔPQR ,, ∠D = ∠P = 70°, ∠F = ∠Q = 80°, P a g e 44 | 159 Available in ykoyyur.blogspot.com, , YK

Page 50 :
SSLC Mathematics Solutions – Part -1, , YK, , 14. Sides AB and AC and median AD of a t r i a n g l e ABC ar e r es p ect i vel y proportional, to sides PQ and PR and median PM of another triangle PQR. Show that ∆ABC ~ ∆PQR, Given: In ΔABC and ΔPQR,, AD and PM are the medians drawn to, BC and QR respectively., , =, , and, , =, , To prove: ΔABC ~ ΔPQR, Construction: Produce AD to E such that, AD = DE, join CE, and produce PM to N such that PM = MN, join RN, Proof: In ΔABD and ΔCDE,, AD = DE, [Construction], BD = DC, [AD is Median], ∠ADB = ∠CDE [Vertically opposite angles], ∴ ΔABD ≅ ΔCDE [SAS Congruency rule], ⇒ AB = CE, [By CPCT], -------------(i), Similarlly, In ΔPQM and ΔMNR,, ⇒ PQ = RN, [By CPCT], -------------(ii), But,, , =, , =, , ⇒, , =, , =, , ⇒, , =, , =, , ⇒, , =, , =, , [Given], [ From (i) and (ii) ], , [∵ 2AD = AE ªÀÄvÀÄÛ 2PM = PN], , ∴ ΔACE ~ ΔPRN [SSS similarity criteria], ∴ ∠2 = ∠4, Similarlly, ∠1 = ∠3, ∴ ∠1 + ∠2 = ∠3 + ∠4, ⇒ ∠A = ∠P, --------------(iii), In ΔABC and ΔPQR,, , =, , [ Given ], , ∠A = ∠P, [From (iii)], ∴ ΔABC ~ ΔPQR [SAS similarity criteria], 15. A vertical pole of length 6 m casts a shadow 4 m long on the ground and at the same time, a tower casts a shadow 28 m long. Find the height of the tower., Length of the vertical Pole = AB = 6m, Length of the shadow casts by the Pole = BC = 4 m, Length of the shadow casts by the Tower = EF = 28 m, Let the height of the tower = DE = h ‘m, In ΔABC and ΔDEF,, P a g e 49 | 159 Available in ykoyyur.blogspot.com

Page 51 :
SSLC Mathematics Solutions – Part -1, , YK, , ∠C = ∠F [The angles make by sun at same time], ∠B = ∠E = 90°, ∴ ΔABC ~ ΔDEF [AA similarity criteria], , =, , ∴, ∴, , [corresponding sides of the similar triangles], , =, , ⇒ h = 6×, , = 6 × 7 ⇒ h = 42 m, , ∴ Height of the tower = 42 m., 16. If AD and PM ar e median s of tr ian gles ABC an d PQR, r espectively wher e, ∆ABC ~ ∆PQR prove that, =, ΔABC ~ ΔPQR [Given], ∴, , =, , =, , -------------- (1), , and ∠A = ∠P, ∠B = ∠Q, ∠C = ∠R --------- (2), AD and PM are the Medians, ∴ BD =, , and QM =, , ----------(3), , From equations (i) and (iii), we get, , =, , ∴, , =, , ----------(4), , In ΔABD and ΔPQM,, ∠B = ∠Q [ From (2) ], [ From (iv)À], , =, , ∴ ΔABD ~ ΔPQM [SAS similarity criteria], ⇒, , =, , 2.5 Areas of Similar Triangles, The ratio of the areas of two similar triangles is equal to the, square of the ratio of their corresponding sides., , Given: ∆ABC ~ ∆PQR, To Prove:, , (, , ), , (, , ), , =, , =, , =, , Construction: Draw AM⟘BC and PN⟘QR, ProofÉ:, , (, , ), , (, , ), , =, , =, , - - -(1) [Area of triangle= xbasexheight], , In ∆ABM and ∆PQN,, ∠B = ∠Q [Corresponding angles of the similar triangle], P a g e 50 | 159 Available in ykoyyur.blogspot.com

Page 52 :
SSLC Mathematics Solutions – Part -1, , YK, , ∠M = ∠N = 900 [Construction], ∴ ∆ABM ~ ∆PQN [AA similarity criteria], ⇒, , =, , - - - - - - (2), , But, ∆ABC ~ ∆PQR [Given], ∴, =, =, ⇒, , =, , ∴, , [ From (2) and (3)], , (, , ), , (, , ), , ⇒, , - - - - (3), , =, , (, , ), , (, , ), , (, , ), , (, , ), , - ------- [From (1) and (3)], , x, =, , =, , =, , =, , [From (3)], , Example 9 : In Fig. 2.43, the line segment XY is parallel to side AC of ∆ABC and it, divides the triangle into two parts of equal areas. Find the ratio, Solution: XYǁAC [Given], ∠ BXY = ∠A [Corresponding angles], ∠ BYX = ∠C [Corresponding angles], ∴ ∆ABC ~ ∆XBY [AA similarity criteria], Area(, , ), , Area(, , ), , =, , ------- (1), , [Theorem 2.6], , But, Area(ABC) = 2 Area (XBY) [Given], (, , ), , (, , ), , =, , =, =, , -------- (2), , [ from (1) and (2)], , √, √, , =, , Or, , [Taken reciprocals], , √, , ⇒ 1 -, , = 1 =, , √, , √, , ⇒, , √, , =, , √, , √, , =, , √, , Exercise 2.4, 1. Let ∆ABC ~ ∆DEF and their areas be, respectively, 64 cm 2 and 121 cm2 . If EF =, 15.4 cm, find BC., ΔABC ~ ΔDEF [Given], Area ΔABC = 64 cm2 and area ΔDEF = 121 cm2; EF = 15.4 cm, (, , ), , (, , ), , =, , =, , =, , [∵ ΔABC ~ ΔDEF], , =, , ⇒, , =, , ⇒, , =, , ⇒, , =, , ., , P a g e 51 | 159 Available in ykoyyur.blogspot.com, , ------------(i)

Page 53 :
SSLC Mathematics Solutions – Part -1, , YK, , x15.4 ⇒ BC = 8 × 1.4, , ⇒ BC =, , ⇒ BC = 11.2 cm, 2. Diagonals of a trapezium ABCD with AB || DC intersect each other at the point O. If, AB = 2 CD, find the ratio of the areas of triangles ∆AOB and ∆COD, Solution: In trapezium ABCD, AB || DC,, Diagonals AC and BD intersect each other at O, In ΔAOB and ΔCOD,, ∠1 = ∠2 [Alternate angles], ∠3 = ∠4 [Alternate angles], ∠5 = ∠6 [Vertically opposite angles], ∴ ΔAOB ~ ΔCOD [AAAsimilarity criteria], Area(, , ), , ⇒ Area(, ⇒, , ), , =, , Area(, , ), , Area(, , ), , =, , =, , (, , ), , [∴ AB = 2CD], , =, , ∴ The ratio of the areas of triangles ΔAOB and ΔCOD is = 4:1, 3. In Fig. 2.44, ABC and DBC are two triangles on the same base BC. If AD intersects BC at, (, ), O, show that ( ) =, Construction: Draw AP⟘ BC and DM ⟘BC, Area(, , ), , Proof: Area(, , ), , =, , =, , -------- (1), , In ΔAPO and ΔDMO,, ∠APO = ∠DMO = 90 0, ∠AOP = ∠DOM [Vertically opposite angles], ∴ ΔAPO ~ ΔDMO [AA similarity criteria], ⇒, =, -------------- (2), ⇒, , Area(, , ), , Area(, , ), , Area(, , ), , Area(, , ), , =, , [ From (1) and (2)], , 4. If the areas of two similar triangles are equal, prove that they are congruent., Given : ΔABC ~ ΔPQR and Area ΔABC = AreaΔPQR, To prove: ΔABC ≅ ΔPQR, Proof : ΔABC ~ ΔPQR, , ⇒, , ⇒1=, , =, , [Area(ABC)= Area(PQR)], , ⇒ BC2 = QR2 ⇒ BC = QR, Similarlly, AB = PQ and AC = PR, ∴ ΔABC ≅ ΔPQR [SSS congruency rule], 5. D, E and F are respectively the mid-points of sides AB, BC and CA of ∆ABC. Find the, ratio of the areas of ∆DEF and ∆ABC., Solution:, In ΔABC, D,E and F are the mid-points of AB, BC and AC respectively, ∴ DF = BC, DE = AC, ªÀÄvÀÄÛ EF = AB[Mid-point theorem], In ΔDEF and ΔCAB,, = = =, P a g e 52 | 159 Available in ykoyyur.blogspot.com

Page 54 :
SSLC Mathematics Solutions – Part -1, , YK, , ∴ ΔDEF ~ ΔCAB, ∴, , Area(, , ), , Area(, , ), (, , ⇒, ⇒, , =, ), , (, , =, , ), , Area(, , ), , Area(, , ), , = [ Area∆ABC = Area∆CAB], , ⇒ Area(DEF) : Area(ABC) = 1: 4, 6. Prove that the ratio of the areas of two similar triangles is equal to the square of the ratio, of their corresponding medians., Solution: ΔABC ~ ΔDEF [Given], Area(, , ), , ∴ Area(, ⇒, , ), , =, , =, , and, , =, , =, , =, , ---------(1), , In ΔABM and ΔDEN,, ∠B = ∠E [ΔABC ~ ΔDEF], =, [from (1)], ∴ ΔABM~ ΔDEN [SAS similarity criteria], ⇒ =, ∴, , 7., , Area(, , ), , Area(, , ), , =, , =, , Prove that the area of an equilateral triangle described on one side of a square is equal, to half the area of the equilateral triangle described on one of its diagonals, Solution: ΔAPB and ΔAQC are equilateral triangles, ∴ ΔAPB ~ ΔAQC [AAA Similarity criteria], ∴, , (, , ), , (, , ), , ⇒, ⇒, , =, , (, , ), , (, (, , ), ), , (, , ), , =, , √, , [Diagonal of a square = √2side], , =, , ⇒ Area(APB) = × Area(AQC), Tick the correct answer and justify :, 8. ABC and BDE are two equilateral triangles such that D is the mid-point of BC. Ratio of, the areas of triangles ABC and BDE is, A) 2 : 1, B) 1 : 2, C) 4 : 1, D) 1 : 4, ΔABC and ΔBDE are equilateral triangle. D is the mid-point of BC, ∴ BD = DC = BC, Let the sides of ΔABC = 2a, ⇒ the sides of ΔBDE = a, ΔABC ~ ΔBDE, ∴, , Area(, , ), , Area(, Area(, , ), ), , Area(, , ), , ⇒, , =, =, , (, , ), , =, , =, , ∴ Ans: (C) 4:1, P a g e 53 | 159 Available in ykoyyur.blogspot.com

Page 55 :
SSLC Mathematics Solutions – Part -1, , YK, , 9. Sides of two similar triangles are in the ratio 4 : 9. Areas of these triangles are in the ratio, A) 2 : 3 B) 4 : 9 C) 81 : 16 D) 16 : 81, ΔABC ~ ΔDEF and, ∴, , Area(, , ), , Area(, Area(, , ), ), , Area(, , ), , ⇒, , =, , =, =, , =, , ∴ Ans : (D) 16:81, , 2.6 Pythagoras Theorem, If a perpendicular is drawn from the vertex of the right angle, of a right triangle to the hypotenuse then triangles on both, sides of the perpendicular are similar to the whole triangle and, to each other., In a right triangle, the square of the hypotenuse is equal to the, sum of the squares of the other two sides., , In a triangle, if square of one side is equal to the sum of the, squares of the other two sides, then the angle opposite the first, side is a right angle., , Theorem 2.8: In a right triangle, the square of the hypotenuse is equal to the sum of, the squares of the other two sides., Given: In ⊿ABC, ∠B = 900, To Prove: AC2 = AB2 + BC2, Consruction: Draw BD⟘AC, Proof: In ∆ADB and ∆ABC, ∠B = ∠D = 900, ∠A = ∠A [Common angle], ∆ADB ~ ∆ABC [AA similarity criteria], ⇒, =, ⇒ AD.AC = AB2, --------- (1), In ∆BDC and ∆ABC, ∠B = ∠D = 900, ∠C = ∠C [Common angle], ∆BDC ~ ∆ABC [AA similarity criteria], ⇒, =, P a g e 54 | 159 Available in ykoyyur.blogspot.com

Page 56 :
SSLC Mathematics Solutions – Part -1, ⇒ CD.AC = BC2, , YK, , --------- (2), , AD.AC + CD.AC = AB2 + BC2 [ By adding (1) and (2)], ⇒ AC (AD+CD) = AB2 + BC2, ⇒ AC × AC = AB2 + BC2, ⇒ AC2 = AB2 + BC2, Theorem2 .9: In a triangle, if square of one side is equal to the sum of the squares of, the other two sides, then the angle opposite the first side is a right angle., Given: In ∆ABC, AC2 = AB2 + BC2, To prove: ∠B = 900, Construction: Draw ∆PQR such that, ∠Q = 900 and PQ = AB, QR = BC, Proof :, In ∆PQR,, PR2 = PQ2 + QR2 [by Pythogoras theorem], PR2 = AB2 + BC2 [Construction], ----------- (1), But, AC2 = AB2 + BC2 [Given], ∴ AC = PR, , -----------(2), , [from (1) and (2)] -----------(3), , AB = PQ [Construction], BC = QR [Construction], AC = PR [from (3)], ∴ ∆ABC ≅ ∆PQR [SSS congruency rule], ∴ ∠B = ∠Q [By CPCT], But, ∠Q = 900 [Construction], ∴ ∠B = 900, Example10: In Fig. 2.48, ∠ACB = 90° and CD⟘AB prove that, , =, , Solution: ∆ACD ~ ∆ABC [Theorem 2.7], ∴, , =, , ⇒ AC2 = AD.AB, , ----------------- (1), , ∆BCD ~ ∆BAC [Theorem 2.7], ∴, , =, , ⇒ BC2 = BA.BD ---------------(2), , dividing (2) by (1), , =, , x, , =, , Example 11 : A ladder is placed against a wall such that its foot is at a distance of, 2.5 m from the wall and its top reaches a window 6 m above the ground. Find the length, of the ladder., Solution:, Let AB is a ladder, CA is a wall and A is a window, ∴BC = 2.5m ªÀÄvÀÄÛ CA = 6m, AB2 = BC2 + CA2 [by Pythagoras theorem], AB2 = (2.5)2 + 62, AB2 = 6.25 + 36, AB2 = 42.25, P a g e 55 | 159 Available in ykoyyur.blogspot.com

Page 58 :
SSLC Mathematics Solutions – Part -1, , YK, , Adding (1) and (2),, OB2 + OD2 = BP2 + OP2 + OQ2 + DQ2, OB2 + OD2 = CQ2 + OP2 + OQ2 + AP2 [ BP=CQ and DQ=AP], OB2 + OD2 = CQ2 + OQ2 + OP2 + AP2, OB2 + OD2 = OC2 + OA2 [from (3) and (4)], , Exercise 2.5, 1. Sides of triangles are given below. Determine which of them are right triangles.In, , case of a right triangle, write the length of its hypotenuse., i) 7cm, 24cm, 25cm, ii) 3cm, 8cm, 6cm, iii) 50cm, 80cm, 100cm, iv) 130cm, 12cm, 5cm, (i) 7 cm, 24 cm and 25 cm., Squaring the numbers 49, 576, and 625., 49 + 576 = 625, (7)2 + (24)2 = (25)2, ∴ Converse of Pythagoras theorem, It is a right triangle., Length of the hypotenuse = 25cm, (ii) 3 cm, 8 cm and 6 cm., Squaring the numbers, 9, 64, and 36., 9 + 36 ≠ 64, ⇒ 32 + 62 ≠ 82, It is not a right triangle, (iii) 50 cm, 80 cm and 100 cm., Squaring the numbers 2500, 6400 and 10000., 2500 + 6400 ≠ 10000, ⇒ 502 + 802 ≠ 1002, It is not a right triangle, (iv) 13 cm, 12 cm and 5 cm., Squaring the numbers 169, 144, and 25., 144 +25 = 169, ⇒122 + 5 2 = 132, ∴ Converse of Pythagoras theorem, It is a right triangle., Length of the hypotenuse = 13cm, 2. PQR is a triangle right angled at P and M is a point on QR such that PM⟘QR. Show, that PM2 = QM . MR, Solution: In ΔPQM, ∠P = 900 and PM⟘QR, ∴ ∆PQM ~ ∆RPM [Theorem 2.7], ⇒ =, ⇒PM2 = QM. MR, 3. In Fig. 2.53, ABD is a triangle right angled at A and AC⟘BD. Show that, P a g e 57 | 159 Available in ykoyyur.blogspot.com

Page 63 :
SSLC Mathematics Solutions – Part -1, ⇒ AE2 =, 2, , (v), , YK, , =, 2, , 4AE = 3a, ⇒ 4 × (height)2 = 3 × (Side)2, Tick the correct answer and justify :, In ∆ABC, AB = 6√ cm, AC = 12 cm and BC = 6 cm∆ABC AiÀÄ°è AB = 6√ cm, AC = 12cm, the angle B is,, A) 120 0, B) 600 C) 900, D) 450, AB = 6√3cm, AC = 12 cm, and BC = 6 cm, AB2 = 108, AC2 = 144 and BC2 = 36, AB2 + BC2 = AC2, 108 + 36 = 144, ∴ ∠B = 90°, The ans is C).900, , 2.7 Summary, 1. Two figures having the same shape but not necessarily the same size are called similar figures., 2. All the congruent figures are similar but the converse is not true, 3. Two polygons of the same number of sides are similar, if (i) their corresponding angles are, equaland (ii) their corresponding sides are in the same ratio (i.e., proportion)., 4. If a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct, points, then the other two sides are divided in the same ratio., 5. If a line divides any two sides of a triangle in the same ratio, then the line is parallel to the third, side., 6. If in two triangles, corresponding angles are equal, then their corresponding sides are in the, same ratio and hence the two triangles are similar (AAA similarity criterion)., 7. If in two triangles, two angles of one triangle are respectively equal to the two angles of the, other triangle, then the two triangles are similar (AA similarity criterion)., 8. If in two triangles, corresponding sides are in the same ratio, then their corresponding angles, are equal and hence the triangles are similar (SSS similarity criterion)., 9. If one angle of a triangle is equal to one angle of another triangle and the sides including these, angles are in the same ratio (proportional), then the triangles are similar (SAS similarity, criterion)., 10. The ratio of the areas of two similar triangles is equal to the square of the ratio of their, corresponding sides., 11. If a perpendicular is drawn from the vertex of the right angle of a right triangle to the, hypotenuse, then the triangles on both sides of the perpendicular are similar to the whole, triangle and also to each other., 12. In a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other, two sides (Pythagoras Theorem)., 13. If in a triangle, square of one side is equal to the sum of the squares of the other two sides,, then the angle opposite the first side is a right angle., , P a g e 62 | 159 Available in ykoyyur.blogspot.com

Page 64 :
SSLC Mathematics Solutions – Part -1, , YK, , Pair of Linear Equations in, two Variables, Linear equation with one variable: The algebraic equation of the type, ( ≠, , and, , are real numbers,, , +, , =, , − variable is called linear equation of one variable., , These type of equations having only one solution., Example :, , +, , =, , ⟹, , =− ⟹, , =, , 3.2 Pair of Linear Equations in Two Variables, 2x + 3y = 5 ;, x - 2y - 3 = 0 and, x - 0y = 2, ⇒ x = 2, An equation which can be put in the form ax + by + c = 0, where a, b and c are real numbers,, and a and b are not both zero, is called a linear equation in two variables x and y. A solution, of such an equation is a pair of values, one for x and the other for y, which makes the two, sides of the equation equal., In fact, this is true for any linear equation, that is, each solution (x, y) of a linear equation, in two variables, ax + by + c = 0, corresponds to a point on the line representing the, equation, and vice versa., 2x + 3y=5; x - 2y - 3 = 0, These two linear equations are in the same two variables x and y. Equations like these are, called a pair of linear equations in two variables., The general form for a pair of linear equations in two variables x and y is,, +, + = 0 and, +, + =0, Here, , , ,, , ,, are real numbers, Some examples of pair of linear equations in two variables are:, (i) 2x + 3y - 7 = 0 ; 9x - 2y + 8 = 0, (ii) 5x = y ; -7x + 2y + 3 = 0, (iii) x + y = 7 ; 17 = y, Two lines in a plane, only one of the following three possibilities can happen:, (i) The two lines will intersect at one point., (ii) The two lines will not intersect, i.e., they are parallel., (iii) The two lines will be coincident., , Example 1: Akhila goes to a fair with Rs 20 and wants to have rides on the Giant Wheel, and play Hoopla. Represent this situation algebraically and graphically (geometrically)., , P a g e 63 | 159 Available in ykoyyur.blogspot.com

Page 65 :
SSLC Mathematics Solutions – Part -1, , YK, , Solution: The pair of equations formed is :, y = x ⇒ 2y = x, ⇒ x – 2y = 0, , (1) and, , 3x + 4y = 20, , (2), , Let us represent these equations graphically., For this, we need at least two solutions for, each equation., x, 0, 2, y=, , 2, , x, y=, , 1, , 0, , 4, , 8, , 5, , 2, , -1, , Example 2 : Romila went to a stationery shop and purchased 2 pencils and 3 erasers for, Rs 9. Her friend Sonali saw the new variety of pencils and erasers with Romila, and she, also bought 4 pencils and 6 erasers of the same kind for Rs 18. Represent this situation, algebraically and graphically., Solution : Let us denote the cost of 1 pencil by x’ and one eraser by y’. Then the algebraic, representation is given by the following equations:, 2x + 3y = 9 -------------(1), 4x + 6y = 18 -----------(2), (1) ⇒ 3y = 9 - 2x, y=, x, y=, , 0, , 3, , 6, , 3, , 1, , -1, , (2) ⇒ 6y = 18 – 4x, y=, x, y=, , 0, , 3, , 6, , 3, , 1, , -1, , E xa mple 3 : Two r a ils a r e r ep r es ent ed b y t h e equa t ions x + 2y – 4 = 0, and 2x + 4y – 12 = 0 Represent this situation geometrically., , P a g e 64 | 159 Available in ykoyyur.blogspot.com

Page 66 :
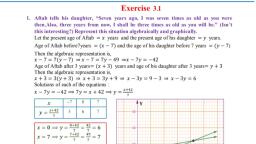
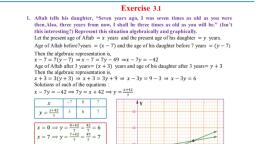
SSLC Mathematics Solutions – Part -1, , YK, , Solution : Two solutions of each of the equations :, + 2 = 4 and 2 + 4 = 12, +2 =4 ⟹2 =4−, ⟹ =, , =, , 0, , 4, , 2, , 0, , 2 + 4 = 12 ⟹, , =, , =, , 0, , 6, , 3, , 0, , Exercise 3.1, 1. Aftab tells his daughter, “Seven years ago, I was seven times as old as you were, then.Also, three years from now, I shall be three times as old as you will be.” (Isn’t, this interesting?) Represent this situation algebraically and graphically., Let the present age of Aftab = years and the present age of his daughter = years., Age of Aftab before7years = ( − 7) and the age of his daughter before 7 years = ( − 7), Then the algebraic representation is,, − 7 = 7( − 7) ⇒ − 7 = 7 − 49 ⇒ − 7 = −42, Age of Aftab after 3 years= ( + 3) years and age of his daughter after 3 years= + 3, Then the algebraic representation is,, + 3 = 3( + 3) ⇒ + 3 = 3 + 9 ⇒ − 3 = 9 − 3 ⇒ − 3 = 6, Solutions of each of the equations :, − 7 = −42 ⟹ 7 = + 42 ⟹ =, -7, , 0, , 7, , 5, , 6, , 7, , =, =, , ⟹, , =, , =, , =, , =, , ⟹, , =, , =, , =, , −3 =6⟹, , =, =6⟹y=, , =, 6, , 3, , 0, , 0, , -1, , -2, , = =0, , x=3⟹y=, , =, , = −1, , x=0⟹y=, , =, , = −2, , The two lines are intersecting each other. There fore there, is a unique solution. The coordinates of intersecting, point are (42, 12), , P a g e 65 | 159 Available in ykoyyur.blogspot.com

Page 67 :
SSLC Mathematics Solutions – Part -1, , YK, , 2. The coach of a cricket team buys 3 bats and 6 balls for Rs 3900. Later, she buys another bat and, 3 more balls of the same kind for Rs1300. Represent this situation algebraically and, geometrically., Let no.of bats = , Let no.of balls = . Then the algebraic representation is,, 3 + 6 = 3900 and + 3 = 1300, 3 + 6 = 3900 ⟹ 6 = 3900 − 3 ⟹ =, , 300, , 100, , 500, , =, , + 3 = 1300 ⟹, , -100, , 600, , 700, , = 100 ⟹, = −100 ⟹, , =, =, =, , (, , ), , (, , ), (, , =, , = 500, , =, , = 600, , ), , =, , = 700, , =, , x = 400 ⟹ y =, , =, , = 300, , x = 700 ⟹ y =, , =, , = 200, , x = 1000 ⟹ y =, , =, , = 300 ⟹, , =, , = 100, , 400, , 700, , 1000, , 300, , 200, , 100, , The two lines are intersecting each other., There fore there is a unique solution. The, coordinates of intersecting point are (1300, 0), 3. The cost of 2 kg of apples and 1kg of grapes on a day was found to be Rs160. After a, month, the cost of 4 kg of apples and 2 kg of grapes is Rs 300. Represent the situation, algebraically and geometrically., Let the cost of apples/ kg = Rs x, the cost of grapes/kg = Rs y, Then the algebraic representation is,, 2 + = 160;, 4 + 2 = 300, 2 + = 160 ⟹ = 160 − 2, , =, , −, , 50, , 60, , 70, , 60, , 40, , 20, , 4 + 2 = 300 ⟹, , =, , =, , 70, , 80, , 75, , 10, , -10, , 0, , Both lines are parallel to each other. There, fore there are no solutions for thes equations., , P a g e 66 | 159 Available in ykoyyur.blogspot.com

Page 68 :
SSLC Mathematics Solutions – Part -1, , YK, , 3.3. Graphical Method of Solution of a Pair of Linear Equations, Consistent pair : A pair of linear equations in two variables, which has, a solution, is called a consistent pair of linear equations., Dependent pair : A pair of linear equations which are equivalent has, infinitely many distinct common solutions. Such a pair is called a, dependent pair of linear equations in two variables., Inconsistent pair : A pair of linear equations which has no solution, is, called an inconsistent pair of linear equations., a x + b y + c = 0, a x + b y + c = 0 JA§ JgÀqÀÄ ¸À«ÄÃPÀgÀtUÀ½UÉ,, , Comparing, the ratios, , Representing, on graph, , Algebraic, solution, , Consistency, , a, b, ≠, a, b, , Intersecting, each other, , Unique, solution, , Consistant, , a, b, c, =, =, a, b, c, , coincident, lines., , Infinite, sulutions, , dependent, , a, b, c, =, ≠, a, b, c, , Parallel lines, , No solutions, , Inconsistent, , Example 4 : Check graphically whether the pair of equations, 1) +, =, ( ) and, −, =, ( ), is consistent. If so, solve them graphically., +3 =6⟹3 =6− ⟹ =, =, , ⟹, , =, , = =, , =, , ⟹, , =, , = =, , =, , 0, , 6, , 2, , 0, , P a g e 67 | 159 Available in ykoyyur.blogspot.com

Page 69 :
SSLC Mathematics Solutions – Part -1, 2 − 3 = 12 ⟹ 3 = 2 − 12 ⟹, =, , ⟹, , =, , =, , ⟹, , =, , ( ), , =, , ( ), , =, , =−, , =, , YK, , =−, , =, , 0, , 3, , -4, , -2, , Both lines are intersecting at the point (6,0). Therefore the solution of the equation is, and = 0 ⇒ The equations are consistant pair., , =6, , Example 5 : Graphically, find whether the following pair of equations has no solution,, unique solution or infinitely many solutions:, −, + =, ( ), −, + =, ( ), Multiplying equation (2) by, 3, −, +, 5 −8 +1 = 0, , =0, , But, this is the same as Equation (1). Hence the lines represented by Equations (1)and (2), are coincident. Therefore, Equations (1) and (2) have infinitely many solutions., Example 6 : Champa went to a ‘Sale’ to purchase some pants and skirts. When her, friends asked her how many of each she had bought, she answered, “The number of, skirts is two less than twice the number of pants purchased. Also, the number of skirts is, four less than four times the number of pants purchased”. Help her friends to find how, many pants and skirts Champa bought., Let us denote the number of pants by x and the number of skirts by y., Then the equations are:, = 2 −2, (1), = 4 −4, (2), y = 2x − 2, x = 2 ⟹ y = 2( 2) − 2 = 4 − 2 = 2, x = 1 ⟹ y = 2( 1) − 2 = 2 − 2 = 0, x = 0 ⟹ y = 2(0) − 2 = 0 − 2 = −2, =, , −, , 2, , 1, , 0, , 2, , 0, , -2, , y = 4x − 4, x = 0 ⟹ y = 4(0) − 4 = 0 − 4 = −4, x = 1 ⟹ y = 4( 1) − 4 = 4 − 4 = 0, , =, , −, , 0, , 1, , -4, , 0, , The two lines intersect at the point (1, 0)., So, x = 1, y = 0 is the required solution of the, pair of linear equations, i.e., the number of pants, she purchased is 1 and she did not buy any skirt., , P a g e 68 | 159 Available in ykoyyur.blogspot.com

Page 70 :
SSLC Mathematics Solutions – Part -1, , YK, , Exercise 3.2, 1. Form the pair of linear equations in the following problems, and find their solutions, graphically., (i) 10 students of Class X took part in a Mathematics quiz. If the number of girls is 4 more, than the number of boys, find the number of boys and girls who took part in the quiz., (ii) 5 pencils and 7 pens together cost Rs 50, whereas 7 pencils and 5 pens together, cost Rs 46. Find the cost of one pencil and that of one pen, (i) Let the number of girls be number of boys be, + = 10, (1) ;, − =4, (2), +, , (1), , = 10 ⟹, , =5⟹, =4⟹, =6⟹, =, , 5, , 4, , 6, , 5, , 6, , 4, , =4⟹, , =5⟹, =4⟹, =3⟹, , =, , = 10 − 5 = 5, = 10 − 4 = 6, = 10 − 6 = 4, , −, , (2)⇒ −, , = 10 −, , =, , −4, , = 5−4 = 1, = 4−4 = 0, = 3 − 4 = −1, , −, , 5, , 4, , 3, , 1, , 0, , -1, , Two lines are intersecting at the point (7, 3), ∴ The solution is: x = 7, y = 3, ⇒Number of Girs = 7, Number of boys = 3, (ii) Let the cost of a pencil be Rs , and the cost of a pen is Rs, 5 + 7 = 50, and 7 + 5 = 46, 5 + 7 = 50 ⟹ =, x=3⟹y=, , Then the equation are:, , ( ), , =, = =5, (, ), 50 − 5 10, 50 − 50, x = 10 ⟹ y =, =, =0, 7, 7, 50 − 5(−4) 70, x = −4 ⟹ y =, =, = 10, 7, 7, , =, , 3, , 10, , -4, , 5, , 0, , 10, , 7x + 5y = 46, ⟹ 5y = 46 − 7x ⟹ y =, x=8⟹y=, x=3⟹y=, x = −2 ⟹ y =, , ( ), ( ), (, , =, , =, , =, , =, , ), , =, , = −2, =5, =, , = 12, , =, , Two lines are intersecting at the point (3, 5). ∴ The solution is:, P a g e 69 | 159 Available in ykoyyur.blogspot.com, , 8, , 3, , -2, , -2, , 5, , 12, , x = 3, y = 5

Page 71 :
SSLC Mathematics Solutions – Part -1, , YK, , Therefore the cost of pencil = Rs 3; The cost of pen = Rs 5, 1), , ,, , On comparing the ratios, , ,, , find out whether the lines representing the following, , pair of linear equations intersect at a point, parallel or coincident., (i) 5 − 4 + 8 = 0 (ii) 9 + 3 + 12 = 0 (iii) 6 − 3 + 10 = 0, 7 + 6 − 9 = 0, 18 + 6 + 24 = 0, 2 −, + 9 = 0, (i), −, +, =, +, −, =, Comparing these with, +, +, = 0 and, +, +, = 0 we get, = 5,, = −4,, = 8 and, = 7,, = 6,, = −9, , = ,, , =, , =, , ∴, , ≠, , ∴ The pair of lines intersect at a point and have unique solution., (ii), +, +, =, +, +, =, Comparing these with a x + b y + c = 0 and a x + b y + c = 0 we get, a = 9, b = 3, c = 12 and a = 18, b = 6, c = 24, , =, , = ,, , = =, , ,, , =, , =, , ∴, , =, , ∴ The pair of lines are coincident.and have infinite solution., (iii), −, +, =, − +, =, Comparing these with, +, +, = 0 and, +, +, = 6,, = −3,, = 10 and, = 2,, = −1,, =9, = =3,, , =, , =3,, , ∴, , =, , =, , =, , = 0 we get, , ≠, , ∴ The pair of lines are parallel and have no solution., , ,, , 2) On comparing the ratios, , and, , find out whether the lines representing the, , following pair of linear equations are consistent or inconsistent?, (i) 3 + 2 = 5 ; 2 − 3 = 7, (ii) 2 − 3 = 8 ; 4 − 6 = 9, (iii), +, = 7 ; 9 − 10 = 14, , (iv) 5 − 3 = 11 ; −10 + 6 = −22, (v), + 2 = 8;, 2 + 3 = 12, +, , (i), = ,, , =, =, , ;, , −, , ∴, , ≠, , =, , ⇒This pair of linear equations are consistent., (ii), −, = ;, −, =, = = ,, = = ,, =, ∴, =, , ≠, , ⇒This pair of equations are inconsistent, (iii), =, , +, , =, , ;, , = × = ,, , −, =, , =, = ×, , =−, , ⇒This pair of linear equations are consistent., P a g e 70 | 159 Available in ykoyyur.blogspot.com, , ∴, , ≠

Page 72 :
SSLC Mathematics Solutions – Part -1, −, , (iv), =, , =, , ;, , =− ,, , −, , =, , +, , =− ,, , YK, , =−, =, , =−, , ∴, , =, , =, , ⇒This pair of linear equations are consistent and have infinite solutions., +, , (v), =, 4., , =, , ;, , +, , = × = ,, , =, , = ,, , =, , =, , ∴, , =, , =, , ⇒This pair of linear equations are consistent and have infinite solutions., Which of the following pairs of linear equations are consistent/inconsistent? If, consistent, obtain the solution graphically:, (i), +, = 5,, 2 + 2 = 10, (ii), –, = 8,, 3 − 3 = 16, (iii) 2 +, − 6 = 0,, 4 − 2 − 4 = 0, (iv) 2 − 2 − 2 = 0,, 4 − 3 − 5 = 0, (i), + = ;, +, =, =, , ,, , =, , ,, , =, , =, , ∴, , =, , =, , ∴ These are coincident lines and have infinite solutions. Hence the pair is consistent., + = 5⟹ =5−, x= 2⟹ y =5−2=3, x= 3⟹ y =5−3=2, x= 4⟹ y =5−4=1, , =, , 2, 3, , −, , 2x + 2y = 10 ⟹, , 3, 2, , 4, 1, , =, , ( ), , x=2⟹y=, , =, =3, 10 − 2(3) 10 − 6, x=3⟹y=, =, =2, 2, 2, ( ), x=4⟹y=, =, =1, , =, (ii), =, , –, , =, ,, , 2, , 3, , 4, , 3, , 2, , 1, , ;, =, , −, =, , =, ,, , =, , =, , ∴, , =, , ≠, , ∴ These are parallel lines and have no solutions.Hence the pair is inconsistent., (iii), + – = ;, −, −, =, =, , = ,, , =, , =−, , ∴, , ≠, , ∴these lines are consistent and intersect each other. These lines have unique solution, (2.2). 2 + – 6 = 0 ⟹ = 6 − 2, , P a g e 71 | 159 Available in ykoyyur.blogspot.com

Page 73 :
SSLC Mathematics Solutions – Part -1, =0⟹, =1⟹, =2⟹, =, 4, , = 6 − 2(0) = 6 − 0 = 6, = 6 − 2(1) = 6 − 2 = 4, = 6 − 2(2) = 6 − 4 = 2, , −, , − 2, , 0, , 1, , 2, , 6, , 4, , 2, , − 4 = 0⟹, ( ), , x=1⟹y=, , ( ), , x=2⟹y=, , ( ), , x=3⟹y=, , =, , =, , = =0, , =, , = =2, , =, , = =4, , 1, 0, , =, , 2, 2, , –, –, = ,, , (iv), =, , YK, , =, =, , 3, 4, , ;, , −, , −, ∴, , =, , =, ≠, , ∴ these lines are consistent and intersect each other. These lines have unique solution., 2x – 2y – 2 = 0 ⟹ y =, x=1⟹y=, , ( ), , =, , = =0, , x=2⟹y=, , ( ), , =, , = =1, , =, , = =2, , =3⟹, , ( ), , =, , =, , 1, , 2, , 3, , 0, , 1, , 2, , 4 – 3 –5 = 0 ⟹, =, =, , ⟹, ⟹, , =− ⟹, , =, , ( )−, , =, , ( )−, , =, , =, , =, , = =, , =, , (− )−, , =, =, , =, , ==, , =−, , −, , 2, , 5, , -1, , 1, , 5, , -3, , 5. Half the perimeter of a rectangular garden, whose length is 4 m more than its width, is, 36 m. Find the dimensions of the garden., Let the width of the Garden = , Length = ., Length: = + 4, , =, , +, , 0, , 8, , 16, , 4, , 12, , 20, , P a g e 72 | 159 Available in ykoyyur.blogspot.com, , =, =, =, , ⟹ = + =, ⟹ = + =, ⟹ =, + =

Page 74 :
SSLC Mathematics Solutions – Part -1, Half the perimeter:, = 36 ⟹, + = 36 ⟹ = 36 −, 0, 16, =, , 6., , −, , 36, , +, , = 36, =, =, =, , 36, , 20, , YK, , 0, , ⟹ =, ⟹ =, ⟹ =, , − =, −, =, −, =, , ∴ these lines are consistent and intersect each other. These lines have unique solution (16,20), ⇒Width = 16m Length = 20m, Given the linear equation 2x + 3y – 8 = 0, write another linear equation in two variables, such that the geometrical representation of the pair so formed is:, (i) Intersecting lines (ii) Parallel lines (iii) Coinsident lines, (i) Given equation is 2x + 3y - 8 = 0, If the lines are intersecting then, ≠, Therefor the second equation is 2 + 4 − 6 = 0, =, =1,, =, ⇒, ≠, (ii) If the lines are parallel then, , =, , ≠, , Therefor the the second line is 4 + 6 − 8 = 0, =, =, ,, =, =, ,, = =, (iii) If the lines are coincident then, , =, , ⇒, , =, , ≠, , ⇒, , =, , =, , =, , Therfor the second line is 6 + 9 − 24 = 0, =, =, ,, =, =, ,, =, =, , 6. Draw the graphs of the equations x – y + 1 = 0 and 3x + 2y – 12 = 0. Determine the, coordinates of the vertices of the triangle formed by these lines and the x-axis, and, shade the triangular region., − +1 = 0 ⟹ = +1, 0, , 1, , 2, , 1, , 2, , 3, , 3x + 2y − 12 = 0 ⟹ y =, 0, 2, 6, 3, =, , 4, 0, , =, , +, , x= 0⟹ y =0+1=1, x= 1⟹ y =1+1=2, x= 2⟹ y =2+1=3, , The coordinates of the vertices of the triangle are(2,3) , (−1,0) , (4,0), , 3.4 Algebraic Methods of Solving a Pair of Linear Equations, In the previous section, we discussed how to solve a pair of linear equations graphically. The, graphical method is not convenient in cases when the point representing the solution of, the linear equations has non-integral coordinates, , P a g e 73 | 159 Available in ykoyyur.blogspot.com

Page 75 :
SSLC Mathematics Solutions – Part -1, , YK, , 3.4.1 Substitution Method :, Step 1 : Find the value of one variable, say y in terms of the other variable, i.e., x from either, equation, whichever is convenient., Step 2 : Substitute this value of y in the other equation, and reduce it to an equation in one, variable, i.e., in terms of x, which can be solved., Step 3 : Substitute the value of x (or y) obtained in Step 2 in the equation used in Step 1, to obtain the value of the other variable., We have substituted the value of one variable by expressing it in terms of the other, variable to solve the pair of linear equations. That is why the method is known as the, substitution method., Example 7: Solve the following pair of equations by substitution method:., −, =, ( ), +, =, ( ), Equation (2) ⟹ + 2 = 3, ⟹ = 3−2, (3), Substitute the value of x in equation (1) we get,, 7(3 − 2 ) − 15 = 2 ⇒ 21 − 14 − 15 = 2, −29 = 2 − 21 ⇒ =, =, Substitute, =3−2, , =, , in equation (3),, = 3−, , =, , =, , ∴The solution is, =, ,, =, Example 8: Aftab tells his daughter, “Seven years ago, I was seven times as old as you, were then.Also, three years from now, I shall be three times as old as you will be.”, (Isn’t this interesting?) Represent this situation algebraically and graphically., Let the present age of Aftab be Years, The present age of his daughter be y’ years, The age of Aftab before 7 Years = − 7 Years, The age of his daughter before 7 years = − 7 yeares, − 7 = 7( − 7) ⟹ − 7 + 42 = 0, (1), After 3 years, his age = + 3 years and his daughter’s age = y +3 years, + 3 = 3( + 3) ⟹, −3 = 6, (2), Equation (2) ⟹ = 3 + 6, (3), Substituting the value of in (1) we get,, 3 + 6 − 7 + 42 = 0, 4 = 48 ⇒ = 12, Substituting the value of, in equation we get,, = 3(12) + 6 = 36 + 6 = 42, Therfor the age of Aftab and his daughter is 42 and 12 respectively., Example 9 : Let us consider Example 2 in Section 3.3, i.e., the cost of 2 pencils and3, erasers is Rs 9 and the cost of 4 pencils and 6 erasers is Rs 18. Find the cost of each, pencil and each eraser., Let the cost of pencil be Rs x and the cost of rubber be Rs y , the the equations are, 2 +3 = 9, (1), 4 + 6 = 18, (2), Equation (1) ⟹ 2 = 9 − 3 ⟹ =, (3), Substituting in equation (2) we get,, P a g e 74 | 159 Available in ykoyyur.blogspot.com

Page 76 :
SSLC Mathematics Solutions – Part -1, 4, , YK, , + 6y = 18, , 18 − 6 + 6 = 18, 18 = 18, This statement is true for all values of y. However, we do not get a specific value of y as a, solution. Therefore, we cannot obtain a specific value of x. This situation has arisen because, both the given equations are the same. Therefore, Equations (1) and (2) have infinitely many, solutions., Example:10 Let us consider the Example 3 of Section 3.2. Will the rails cross each other?, + 2 − 4 = 0, (1), 2 + 4 − 12 = 0, (2), Equation (1) ⟹ = 4 − 2, (3), Substituting in equation (2) we get,, 2(4 − 2 ) + 4y − 12 = 0, 8 − 4 + 4 − 12 = 0, 8 − 12 = 0, −4 = 0, which is a false statement. Therefore, the equations do not have a common solution. So, the, two rails will not cross each other., , Exercise 3.3, 1) Solve the following pair of linear equations by substitution method., (i), +, =, ( ), − =, ( ), Equation (1) ⟹ = 14 −, (3), Substituting in equation (2) we get,, 14 − − = 4 ⇒ 14 − 2 = 4, −2 = 4 − 14 ⇒ −2 = −10 ⇒ =, =5, Substituting, = 5 in equation (3), = 14 − = 14 − 5 ⇒ = 9, ∴ = 9, = 5, (ii) − =, ( ), +, =, ( ), Equation (1) ⟹ s = 3 + t, (3), Substituting in equation (2) we get,, , +, , =6 ⇒, , =6, , ⇒ 6 + 5t = 36 ⇒ 5t = 36 − 6 ⇒ t =, Substituting, = 6 in equation (3), s= 3+t ⇒ s= 3+6 ⇒ = 9, ∴ = 9,, =6, (iii), − =, ( ), −, =, ( ), Equation (1) ⟹ = 3 − 3 Substituting in equation (2) we get,, 9 − 3(3 − 3 ) = 9 ⇒ 9 − 9 + 9 = 9, 9=9, P a g e 75 | 159 Available in ykoyyur.blogspot.com

Page 77 :
SSLC Mathematics Solutions – Part -1, , YK, , This statement is true for all values of y. However, we do not get a specific value of y as a, solution. Therefore, we cannot obtain a specific value of x. This situation has arisen because, both the given equations are the same. Therefore, Equations (1) and (2) have infinitely many, solutions., (iv) . + ., = ., ., + ., = ., 0.2 + 0.3 = 1.3, (1) × 10, 0.4 + 0.5 = 2.3, (2) × 10, 2 + 3 = 13, (3), 4 + 5 = 23, (4), ( 5), Equation (3) ⟹ 2 = 13 − 3 ⟹ =, Substituting in equation (4) we get,, 4, + 5 = 23, 26 − 6 + 5 = 23, 26 − 23 = ⇒ = 3 ,, ( ), , =, , =, ∴ = 2,, =3, (v), √ +√, √ −√ =, , = =2, =, , ( ), ( ), , Equation (1) ⟹ √2 = −√3, , −, , √, , √, , − √8 = 0 ⇒ −, , √, , − 2√2, , =0 ⇒, , = 0 , Substituting, , =−, ∴, , √ ( ), √, , −, , =−, , √, , (3), , √, , −, , √, , √, , − √4 × 2, , =0, , − 2√2 = 0, , = 0 in equation (3), , =0, , = 0,, , (vi), , ⟹, , in equation (2) we get,, , Substituting, √3 −, , = 3 in equation (5), , Substituting, , =0, =−, , ( ), , + =, ( ), Equation (1) × 2 ⟹ 3 − 5 = −4, Equation (2) × 6 ⟹ 2 + 3 = 13, , (3), (4), , Equation (3) ⟹ 3 = 5 − 4 ⟹ =, Substituting in equation (4) we get,, 2, , + 3 = 13 ⇒, , (5), , = 13, , 19 − 8 = 39 ⇒ 19 = 39 + 8 ⇒ 19 = 47 ⇒, =, , Substituting, =, , =, , =, , in equation (5)À, × ⇒, , =, , × ⇒, , =, , 2. Solve 2x + 3y = 11 and 2x – 4y = – 24 and hence find the value of ‘m’ for which, y = mx + 3., P a g e 76 | 159 Available in ykoyyur.blogspot.com

Page 78 :
SSLC Mathematics Solutions – Part -1, , YK, , 2 + 3 = 11, (1), 2 − 4 = −24, (2), Equation (2) ⟹ 2 = 4 − 24 ⟹ = 2 − 12, (3), Substituting in equation (1) we get,, 2(2 − 12 ) + 3 = 11, 4 − 24 + 3 = 11 ⇒ 7 = 11 + 24 ⇒ 7 = 35 ⇒ = 5, substituting = 5 in equation (3), = 2x5 − 12 = 10 − 12 = −2, ∴ = −2,, =5, =, + 3, 5 = (−2) + 3, 5 − 3 = −2 ⇒ −2 = 2 ⇒, = = −1, , 3., , Form the pair of linear equations for the following problems and find their solution by, substitution method, (i) The difference between two numbers is 26 and one number is three times the other., Find them., Let the first number be , the second number be , then, > . By the given condition the, equations are, − = 26, (1), =3, (2), Substituting the value of, in equation (1) we get,, 3 − = 26 ⇒ 2 = 26, = 13 , Substitute = 13 in equation (2), = 3(13) = 39, ∴ = 13,, = 39, (ii)The larger of two supplementary angles exceeds the smaller by 18 degrees. Find them., Let the larger angle be , the smaller angle be . If the angles are supplementary then sum, of two angles is 180 , By the given conditions the equations are,, + = 180, (1), = + 18, (2), Substituting the value of, in equation (1) we get,, + 18 + = 180 ⇒ 2 = 162, = 81 Substitute = 81 in equation (2), = 81 + 18 = 99, ∴ = 99 ,, = 81, (iii) The coach of a cricket team buys 7 bats and 6 balls for Rs 3800. Later, she buys 3, bats and 5 balls for Rs 1750. Find the cost of each bat and each ball., Let the cost of a batÉ = Rs, , the cost of a ball = Rs y. the equations are, 7 + 6 = 3800, (1), 3 + 5 = 1750, (2), Equation (1) ⟹ 7 = 3800 − 6 ⟹ =, (3), Substituting the value of in equation (2)we get, 3, + 5 = 1750, = 1750 ⇒ 11400 + 17 = 12250, P a g e 77 | 159 Available in ykoyyur.blogspot.com

Page 79 :
SSLC Mathematics Solutions – Part -1, , YK, , ⇒ 17 = 12250 − 11400 ⇒ 17 = 850 ⇒ =, = 50, Substitute, = 50 in equation (3), ( ), =, =, =, = 500, ∴ The cost of a bat = Rs 500 , The cost of a ball = Rs 50, (iv) The taxi charges in a city consist of a fixed charge together with the charge for the, distance covered. For a distance of 10 km, the charge paid is Rs 105 and for a journey, of 15 km, the charge paid is Rs 155. What are the fixed charges and the charge per, km? How much does a person have to pay for travelling a distance of 25km?, Let the fixed charges be Rs x, the charges/km be Rs . Then the equations are,, + 10 = 105, (1), + 15 = 155, (2), Equation (1) ⟹ = 105 − 10, (3), Substituting the value of in equation (2)we get, 105 − 10 + 15 = 155, 105 + 5 = 155 ⇒ 5 = 155 − 105 ⇒ = = 10, Substitute = 10 in equation (3), = 105 − 10(10) = 105 − 100 = 5, ∴ the fixed charges is Rs 5 and charges per km is Rs 10, The total charges to travel 25km is, + 25 = 5 + 25(10) = 5 + 250 = Rs 255, (v) A fraction becomes if 2 is added to both the numerator and the denominator If, 3, is added to both the numerator and the denominator it becomes Find the fraction., Let the fraction be . By the given condition,, +2 9, =, ⟹ 11 + 22 = 9 + 18, + 2 11, ⟹ 11 − 9 = 18 − 22 ⟹ 11 − 9 = −4, +3 5, = ⟹ 6 + 18 = 5 + 15, +3 6, ⟹ 6 − 5 = 15 − 18 ⟹ 6 − 5 = −3, Equation (1) ⟹ 11 = −4 + 9 ⟹ =, Substituting the value of in equation (2)we get, 6, − 5 = −3 ⇒, = −3, ⇒ −24 − = −33 ⇒ − = −33 + 24 ⇒ − = −9, Subtitute = 9 in equation (3), =, , ( ), , The fraction, , =, , =, , (1), , (2), (3), , =7, , =, , (vi) Five years hence, the age of Jacob will be three times that of his son. Five years ago,, Jacob’s age was seven times that of his son. What are their present ages?, Let age of Jocob = , and age of his son = By the given condition the equations are, After 5 years + 5 = 3( + 5), ⟹ + 5 = 3 + 15 ⟹ − 3 = 10, (1), Before 5 years − 5 = 7( − 5), ⟹ − 5 = 7 − 35 ⟹ − 7 = −30, (2), Equation (1) ⟹ = 10 + 3, (3), P a g e 78 | 159 Available in ykoyyur.blogspot.com

Page 80 :
SSLC Mathematics Solutions – Part -1, , YK, , Substituting the value of in equation (2)we get, 10 + 3 − 7 = −30 ⇒ 10 − 4 = −30, ⇒ −4 = −30 − 10 ⇒ −4 = −40 ⇒ =, = 10, Substitute = 10 in equation (1),, = 10 + 3(10) = 10 + 30 = 40, ∴ Age of Jocob = 40 and age of his son = 10, , 3.4.2 Elimination Method, Example 11 : The ratio of incomes of two persons is 9 : 7 and the ratio of their, expenditures is 4 : 3. If each of them manages to save ` 2000 per month, find their, monthly incomes, Solution: Let the incomes of two persons be Rs 9x and Rs 7x respectively.The expenditure, be Rs 4y and Rs 3y, then we get the equations,, 9x – 4y = 2000, (1), 7x – 3y = 2000, (2), Multiply Equation (1) by 3 and Equation (2) by 4 to make the coefficients of y equal., 9x – 4y = 2000, (1) x 3, 7x – 3y = 2000, (2) x 4, 27x – 12y = 6000, (3), 28x – 12y = 8000, (4), -x, = -2000, ⇒ x = 2000, Substitute x = 2000 in equation (1), we get, 9(2000) – 4y = 2000 ⇒18000 – 2000 = 4y ⇒4y = 16000 ⇒ y = 4000, ∴ The monthly incomes of two persons are = Rs 18000 and Rs 14000, The method used in solving the example above is called the elimination method, because, we eliminate one variable first, to get a linear equation in one variable. In the example, above, we eliminated y. We could also have eliminated x. Try doing it that way., You could also have used the substitution, or graphical method, to solve this problem., Try doing so, and see which method is more convenient., Example 12 : Use elimination method to find all possible solutions of the following pair, of linear equations, 2x + 3y = 8, (1), 4x + 6y = 7, (2), Multiply Equation (1) by 2 to make the coefficients of x equal., 2x + 3y = 8, (1) x 2, 4x + 6y = 16, (3), Substracting (2) from (1) , we get, 4x + 6y = 16, (3), 4x + 6y = 7, (2), 0 = 9, 0 = 9, which is a false statement. Therefore, the pair of equations has no solution, Example 13 : The sum of a two-digit number and the number obtained by reversing the, digits is 66. If the digits of the number differ by 2, find the number. How many such, numbers are there?, Let the two digits number = 10x + y, P a g e 79 | 159 Available in ykoyyur.blogspot.com

Page 81 :
SSLC Mathematics Solutions – Part -1, , YK, , Number after reversing the digits = 10y + x, ∴ 10x + y + 10y + x = 66 ⇒ 11x + 11y = 66 ⇒ x + y = 6, We are also given that the digits differ by 2, therefore,, x– y= 2, (2), substract (2) from (1), x+ y= 6, (1), x– y= 2, (2), 2y = 4, , (1), , ⇒ y= 2, Substitute y = 2 in equation (1), x+2=6 ⇒ x=4, Therfor the number is 10x + y = 10 x 4 + 2 = 42, ⇒Two numbers are 42 and 24, , Exercise 3.4, 1. Solve the following pair of linear equations by the elimination method and the substitution, method :, (i) x + y = 5 ªÀÄvÀÄÛ 2x - 3y = 4, , Eliminating method:, x + y= 5, (1), 2x –3y = 4, (2), Multiply Equation (1) by 2 to make the coefficients of x equal., 2x + 2y = 10, (3), Substracting (2) from (1),, 2x + 2y = 10, (3), 2x – 3y = 4, (2), 5y = 6, ⇒ y=, Substitute y = in equation (1),, x+, , = 5 ⇒ 5x + 6 = 25 ⇒ 5x = 19 ⇒x =, , ∴ x = and y =, Substituting Method:, x + y = 5, 2x – 3y = 4, (1) ⇒ y = 5 - x, Substitute y = 5 – x in (2), ⇒2x – 3(5 – x) = 4, ⇒2x – 15 + 3x = 4 ⇒5x = 19, Substitute x =, +, ∴ x=, , (1), (2), , (3), ⇒x=, , in (1), , y = 5 ⇒19 +, , 5y = 25 ⇒5y = 25 – 19 ⇒y =, , and y =, , P a g e 80 | 159 Available in ykoyyur.blogspot.com

Page 83 :
SSLC Mathematics Solutions – Part -1, (1) ⇒-5y = 4 – 3x ⇒ 5y = 3x – 4 ⇒ y =, Substitute y =, , Substitute x =, 3, , = 7 ⇒45x – 6x + 8 = 35 ⇒39x = 27 ⇒x =, , =, , in (1),, , – 5y = 4 ⇒27 – 65y = 52 ⇒ – 65y = 52 - 27 ⇒ y = −, , ∴À x =, , ⇒y=−, , and y = −, , (iv) +, , = -1 and x -, , =3, , Eliminating Method:, + = -1 ⇒ 3x + 4y = -6, x-, , (3), , in (2), , = 7 ⇒9x –, , 9x – 2, , YK, , ⇒ 3x -, , =3, , (1), , = 9, , Substracting (1) from (2), 3x + 4y = -6, 3x = 9, +5y = - 15, , (2), (1), (2), , ⇒ y= -3, Substitute y = - 3 in (1), 3x + 4(- 3) = -6 ⇒3x - 12 = -6 ⇒3x = 6 ⇒x = 2, ∴ x = 2 and y =−3, Substituting Method:, 3x + 4y = -6, (1), 3x = 9, (2), (2) ⇒ -y = 9 – 3x⇒ y = 3x – 9, (3), Substitute y = 3x – 9 in (1), 3x + 4(3x – 9) = -6 ⇒3x + 12x - 36 = -6 ⇒ 15x = 30 ⇒ x = 2, Substitute x = 2 in (3), y = 3(2) – 9 ⇒y = 6 – 9 ⇒ y = -3, ∴ x = 2 and y =−3, 2. Form the pair of linear equations in the following problems, and find their solutions, (if they exist) by the elimination method :, (i) If we add 1 to the numerator and subtract 1 from the denominator, a fraction reduces to, 1. It becomes if we only add 1 to the denominator. What is the fraction?, Let the fraction =, According to question ,, and, , =, , = 1 ⇒ x + 1 = y – 1⇒ x – y = -2, , ⇒ 2x = y + 1 ⇒ 2x – y = 1, , Substract (1) from (2), x – y = -2, 2x – y = 1, -x, = -3, , (1), (2), , P a g e 82 | 159 Available in ykoyyur.blogspot.com, , (1), , (2)

Page 84 :
SSLC Mathematics Solutions – Part -1, , YK, , ⇒ x= 3, Substitute x = 3 in (1), 3 – y = -2 ⇒ -y = - 2 – 3 ⇒ y = 5, The fraction =, (ii) Five years ago, Nuri was thrice as old as Sonu. Ten years later, Nuri will be twice as old, as Sonu. How old are Nuri and Sonu?, Let the age of Nuri = x and that of Sonu = y .According to question, (x - 5) = 3(y - 5), x - 3y = -10, (1), and, (x + 10y) = 2(y + 10), x - 2y = 10, (2), Substract (1) from (2), x - 3y = -10, (1), x - 2y = 10, (2), - y = -20, ⇒y = 20, Substitute y = 20 in (1), x - 60 = -10 ⇒ x = 50, ∴ The age of Nuri = 50 years and the age of Sonu = 20years, (iii) The sum of the digits of a two-digit number is 9. Also, nine times this number is, twice the number obtained by reversing the order of the digits. Find the number., Let the two digits number = xy , According to question,, x+y =9, 2(10y + x) = 9(10x + y), 20y + 2x = 90x + 9y, 88x – 11y = 0, ⇒ 8x – y = 0, By adding (1) and (2), x+ y= 9, 8x – y = 0, 9x, = 9, , (1), , (2), (1), (2), , ⇒ x=1, Substitute x = 1 in (1), 1 + y= 9 ⇒ y= 8, Therefor the number is xy = 18, (iv) Meena went to a bank to withdraw Rs 2000. She asked the cashier to give her, Rs 50 and Rs 100 notes only. Meena got 25 notes in all. Find how many notes of Rs, 50 and Rs 100 she received, Let the number of Rs 50 notes = x and the number of Rs 100 notes = y. According to qn, x + y = 25, 50x + 100y = 2000, ⇒ x + 2y = 40, , (1) and, (2), , P a g e 83 | 159 Available in ykoyyur.blogspot.com

Page 85 :
SSLC Mathematics Solutions – Part -1, , YK, , Substract (1) from (2), x + 2y = 40, (2), x + y = 25, (1), y = 15, Substitute y = 15 in (1), x + 15 = 25 ⇒ x = 25 – 15 ⇒ x = 10, Therefor the number of Rs 50 notes = 10 and the number of Rs 100 notes = 15, (v) A lending library has a fixed charge for the first three days and an additional charge, for each day thereafter. Saritha paid Rs 27 for a book kept for seven days, while Susy paid, Rs 21 for the book she kept for five days. Find the fixed charge and the charge for each, extra day ., Let the fixed charges for first 3 days Ì = Rs x, The additional charges for remaing days = Rs y According to question, x + 4y = 27, (1), x + 2y = 21, (2), Substract (1) from (2), x + 2y = 21, (2), x + 4y = 27, (1), - 2y = -6, ⇒y = 3, Substitute y = 3 in (1), x + 4x3 = 27 ⇒ x + 12 = 27, ⇒ x = 27 – 12 ⇒ x = 15, The fixed charges = Rs 15 and the additional charges = Rs 3, , 3.4.3 Cross - Multiplication Method, Equations are:, a x + b y + c = 0, a x + b y + c = 0, x=, , y=, =, , [a b − a b ≠ 0], , =, , Example14:From a bus stand in Bangalore , if we buy 2 tickets to Malleswaram and 3, tickets to Yeshwanthpur, the total cost is Rs 46; but if we buy 3 tickets to Malleswaram, and 5 tickets to Yeshwanthpur the total cost is Rs 74. Find the fares from the bus stand, to Malleswaram, and to Yeshwanthpur., , P a g e 84 | 159 Available in ykoyyur.blogspot.com

Page 86 :
SSLC Mathematics Solutions – Part -1, , YK, , Solution: Let Rs x be the fare from the bus stand in Bangalore to Malleswaram, and Rs y to, Yeshwanthpur. From the given information, we have, 2x + 3y = 46, ⇒ 2x + 3y – 46 = 0, (1), 3x + 5y = 74 ⇒ 3x + 5y – 74 = 0, (2), , =, (, , ), , (, , =, ), , ⇒, , =(, , (, , ), , =, , ⇒, ⇒, , =1⇒, , =, , ( ), , ( ), , =, , = 1⇒, , =, , ), , =1⇒x=8, , = 10, , Hence, the fare from the bus stand in Bangalore to Malleswaram is Rs 8 and the fare to, Yeshwanthpur is Rs 10., Example 15 : For which values of p does the pair of equations given below has unique, solution?, 4x + py + 8 = 0, 2x + 2y + 2 = 0, Here, a = 4, b = p, c = 8 and a = 2, b = 2, c = 2, Now for the given pair to have a unique solution : ≠, ⇒ ≠ ⇒p ≠ 4, Therefore, for all values of p, except 4, the given pair of equations will have a unique solution, Example 16 : For what values of k will the following pair of linear equations have, infinitely many solutions?, kx + 3y - (k - 3) = 0, 12x + ky - k = 0, For a pair of linear equations to have infinitely many solutions:, Here,, = k,, = 3, = -(k-3) and, = 12,, = k, = -k, =, ⇒, , =, =, , =, , ⇒, ⇒ =, , = =, (, , (, , ), , ⇒, , = ⇒ k2 = 36 ⇒ k = ±6, , ), , ⇒ 3k = k2 – 3k ⇒ 6k = k2 ⇒ (6k - k2 ) = 0 ⇒ k(6 - k ) = 0 ⇒ k = 0 CxÀªÁ 6 - k = 0 ⇒ k = 6, Therefore, the value of k, that satisfies both the conditions, is k = 6. For this value, the pair of, linear equations has infinitely many solutions., , P a g e 85 | 159 Available in ykoyyur.blogspot.com

Page 87 :
SSLC Mathematics Solutions – Part -1, , YK, , Exercise 3.5, 1., , Which of the following pairs of linear equations has unique solution, no solution, or, infinitely many solutions. In case there is a unique solution, find it by using cross, multiplication method, (i) x - 3y - 3 = 0, 3x – 9y – 2 =0, Here, a = 1, b = -3, c = -3 and a = 3, b = -9, c = -2, , = ;, , =, , =, , ⇒, , = ;, , =, , =, , ≠, , Therefore the given pair of linear equations are parallel and not intersecting each other., Hence the pair has no solution., (ii) 2x + y = 5 ⇒ 2x + y – 5 = 0, 3x + 2y = 8⇒ 3x +2y – 8 = 0, Here a = 2, b = 1, c = -5 and a = 3, b = 2, c = -8, , = ;, , = ;, , =, , =, , ≠, , ⇒, , Therefore the pair of linear equations has unique solution, , =, ⇒, , (, , ), , ⇒, , (, , =, ), , =(, , =, , ), , (, , ), , =, , ⇒ =, , =, , ( ), , ( ), , =, , ⇒ = ⇒x=2, =, , ⇒y = 1, , Therefore x = 2 and y = 1, iii) 3x - 5y = 20 ⇒ 3x – 5y – 20 = 0, 6x - 10y = 40⇒6x – 10y – 40 = 0, Here, a = 3, b = -5, c = -20 and a = 6, b = -10, c = -40, = = ;, ⇒, , =, , =, , = ;, , =, , =, , =, , Therefore the given pair of linear equations are coincident and the pair has infinite solutions., (iv) x - 3y - 7 = 0, 3x - 3y - 15 = 0, P a g e 86 | 159 Available in ykoyyur.blogspot.com

Page 88 :
SSLC Mathematics Solutions – Part -1, , YK, , Here, a = 1, b = -3, c = -7 and a = 3, b = -3, c = -15, , =, , ;, , = 1;, , =, , =, , =, , ≠, , ⇒, , Therefore the pair has unique solution., , =, ⇒, , (, , )(, , ⇒, , =, , ) (, , )(, , ), , =, , ⇒, , =(, , ), , (, , ), , =, , (, , ), , (, , ), , =, , =, , ⇒, , =, , = ⇒ 6x = 24 ⇒x = 4, , = ⇒6y = -6 ⇒ y = -1, There fore x = 4 and y = -1, 2. (i) For which values of a and b does the following pair of linear equations have an, infinite number of solutions?, 2x + 3y = 7 ⇒ 2x + 3y – 7 = 0, (a - b) x + (a + b)y = 3a + b - 2 ⇒ x + (a + b)y – (3a + b – 2) = 0, For a pair of linear equations to have infinitely many solutions: = =, Here, a = 2, b = 3, c = -7 and a = (a - b), b = (a + b), c = -(3a +b – 2), =, =, , (, , ;, , ), , ⇒, , (, , =, ), , =, , (, , ), , (, , ), , ⇒ 2a + 2b = 3a – 3b, ⇒a = 5b, =, , ⇒(, , ), , =(, , ;, , =, , (, , ), , =, , (, , ), , ⇒ 2(a + b) = 3(a – b ), (1), ), , ⇒ 3(3a + b -2) = 7(a+b) ⇒9a + 3b – 6 = 7a + 7b, ⇒2a - 4b = 6 ⇒ a – 2b = 3, (2), From (1) and (2), (2)⇒ 5b – 2b = 3 ⇒ 3b = 3 ⇒ b = 1[∵a = 5b], a = 5b ⇒ a = 5x1 ⇒ a = 5, ⇒ If a = 5 and b = 1 the pair of linear equations has infinite solutions., ii) For which value of k will the following pair of linear equations have no solution?, 3x + y = 1 ⇒ 3x + y – 1= 0, (2k - 1)x + (k - 1)y = 2k + 1 ⇒ (2k - 1)x + (k - 1)y - (2k + 1) = 0, For a pair of linear equations to have no solutions:, P a g e 87 | 159 Available in ykoyyur.blogspot.com, , =, , ≠

Page 89 :
SSLC Mathematics Solutions – Part -1, , YK, , E°è a = 3, b = 1, c = -1 ªÀÄvÀÄÛ a = (2k - 1), b = (k - 1), c = -(2k +1), , =(, , ), , ;, , ⇒(, , =, , =(, ), , =, , ), , (, , ;, , =, , (, , ), , =(, , ), , ), , ⇒ 3(k – 1) = (2k – 1 ) ⇒ 3k – 3 = 2k – 1 ⇒k = 2, Therefore, if k = 2 then the pair of linear equations have no solution., 3. Solve the following pair of linear equations by the substitution and cross-multiplication methods :, 8x + 5y = 9, (1), 3x + 2y = 4, (2), Substitution Method:, –, 8x + 5y = 9 ⇒ 5y = 9 – 8x ⇒ y =, –, , Equation (2) ⇒ 3x + 2y = 4 ⇒ 3x + 2, , =4, , –, , ⇒ 3x +, = 4, Multiplying by 5, 15x + 18 – 16x = 20, ⇒-x = 20 – 18 ⇒ - x = 2 ⇒ x = -2, Substitute x = -2 in (1), 3(-2) + 2y = 4 ⇒ -6 + 2y = 4, ⇒2y = 4 + 6 ⇒2y = 10 ⇒ y = 5, Therefore the solution is: x = -2 ªÀÄvÀÄÛ y = 5, Cross multiplication Method:, 8x + 5y = 9 ⇒ 8x + 5y – 9 = 0, (1), 3x + 2y = 4 ⇒ 3x + 2y – 4 = 0, (2), Here, a = 8, b = 5, c = -9 and a = 3, b = 2, c = -4, , =, ⇒, , ( )(, , ) ( )(, , ⇒, ⇒, , =, , =, ), , =(, , ), , (, , ), , =, , =, , =, , =1⇒, , = 1 ⇒ x = -2, , ( ), , ( ), , = 1⇒ y = 5, Therefore the solution: x = -2 ªÀÄvÀÄÛ y = 5, , 4., , Form the pair of linear equations in the following problems and find their solutions (if, they exists) by any algebraic method., i) A part of monthly hostel charges is fixed and the remaining depends on the number, of days one has taken food in the mess. When a student A takes food for 20 days she has, to pay Rs 1000 as hostel charges whereas a student B, who takes food for 26 days, pays, Rs 1180 as hostel charges. Find the fixed charges and the cost of food per day., P a g e 88 | 159 Available in ykoyyur.blogspot.com

Page 90 :
SSLC Mathematics Solutions – Part -1, , YK, , Let the fixed charge = x and daily food charges = y. According to question, x + 20y = 1000, (1), x + 26y = 1180, (2), Substracting equation (1) from (2), x + 26y = 1180, (2), x + 20y = 1000, (1), 6y = 180, ⇒ y = 30, Substitute y = 30 in equation (1), x + 20 × 30 = 1000 ⇒ x = 1000 – 600 ⇒ x = 400, Therefore the fixed charges = Rs 400 and daily food charges = Rs 30, (ii) A fraction becomes, , when 1 is substracted from the numerator and it becomes, , when 8 is added to its denominator. Find the fraction., , Let the given fraction =, , =, =, , ⇒ 3x - y = 3, ⇒ 4x - y = 8, , According to questions,, (1), (2), , By substracting equation(1) from (2), 4x - y = 8, (2), 3x - y = 3, (1), x, =5, Substituting x = 5 in equation (1), 15 - y = 3 ⇒ y = 12, Therefore the fraction =, iii) Yash scored 40 marks in a test, getting 3 marks for each right answer and losing 1, mark for each wrong answer. Had 4 marks been awarded for each correct answer and 2, marks been deducted for each incorrect answer, then Yash would have scored 50 marks., How many questions were there in the test?, Let the number of right answer = x and the number of wrong answer = y, According to question,, 3x - y = 40, (1) and, 4x - 2y = 50 ⇒ 2x - y = 25, (2), By substracting equation(1) from (2), 2x - y = 25, (2), 3x - y = 40, (1), -x, = -15, ⇒ x = 15, Substituting x = 15 in equation (1), 3(15) - y = 40 ⇒-y = 40 – 45 ⇒-y = -5 ⇒ y = 5, Therefore the right answers = 15 ; Wrong answers = 5; Total questions = 20, P a g e 89 | 159 Available in ykoyyur.blogspot.com

Page 91 :
SSLC Mathematics Solutions – Part -1, , YK, , iv) Places A and B are 100 km apart on a highway. One car starts from A and another, from B at the same time. If the cars travel in the same direction at different speeds, they, meet in 5 hours. If they travel towards each other, they meet in 1 hour. What are the, speeds of the two cars?, Let the speed of car A = x km/h and speed of car B = y km/h, The speed of both car travel in same direction = (x - y) km/h, The speed of both car travel in opposite direction = (u + v) km/h, According to question,, 5(x - y) = 100 ⇒ x - y = 20, (1), 1(x + y) = 100 ⇒ x + y = 100, (2), By adding equation (1) and (2), x - y = 20, (2), x + y = 100, (1), 2x, = 120, ⇒ x = 60, Substituting x = 60 in equation (1), 60 - y = 20 ⇒-y = -40 ⇒y = 40, Therefore the speed of car A and B = 60 km/h and 40 km/h, v) The area of a rectangle gets reduced by 9 square units, if its length is reduced by 5, units and breadth is increased by 3 units. If we increase the length by 3 units and the, breadth by 2 units, the area increases by 67 square units. Find the dimensions of the, rectangle., Let the area = xy According to question,, (x - 5) (y + 3) = xy – 9, ⇒xy + 3x – 5y – 15 = xy – 9 ⇒ 3x - 5y = 6, (x + 3) (y + 2) = xy + 67, , (1), , ⇒xy + 2x +3y + 6 = xy + 67 ⇒ 2x + 3y = 61, 3x - 5y = 6 ⇒ 3x = 6 + 5y ⇒x =, , (2), , Substituting the value of x in equation (1), we get, 2, + 3y = 61 ⇒, + 3y = 61, Multiplying by 3,, ⇒12 + 10y + 9y = 183 ⇒ 19y = 183 - 12 ⇒19y = 171 ⇒ y = 9, Substituting y = 9 in equation (1),, 3x – 5(9) = 6 ⇒ 3x – 45 = 6 ⇒ 3x = 51 ⇒ x = 17, Therefore length of the rectangle = 17 units and bredth = 15 units, , 3.5 Equations Reducible to a Pair of Linear Equations in Two Variables, Example 17:Solve the pair of equations, +, , = 13;, , Solution:, -, , Let, , +, , = -2, , = 13 ⇒ 2, , = -2⇒ 5, = p and, , - 4, , + 3, , = 13, , = -2, , =q, , P a g e 90 | 159 Available in ykoyyur.blogspot.com, , (1), (2)

Page 92 :
SSLC Mathematics Solutions – Part -1, , YK, , (1) ⇒ 2p + 3q = 13, , (3), , (2) ⇒ 5p – 4q = -2, From (3) 2p + 3q = 13 ⇒ 3q = 13 – 2p ⇒ q =, , (4), , in equation (4) we get,, , Substitute q =, 5p – 4, , = -2 ⇒ 5p –, , = -2, , Multiplying by 3,, , ⇒ 15p– 52 + 8 = -6 ⇒ 23p = 46 ⇒ p = 2, Substitute p = 2 in (1) we get,, 2(2) + 3q = 13 ⇒4 + 3q = 13 ⇒3q = 9 ⇒q = 3, ⇒ substituting the value of p and q ,, = p⇒, , = 2⇒x=, , =q ⇒ =3 ⇒ y=, Example 18 : Solve the following pair of equations by reducing them to a pair of, linear equations, , +, , =2, , +, , =1, +, , Solution:, , -, , - 3, , = 1 ⇒6, , = p;, , Let, , = 2 ⇒5, , = 2, , = 1, , =q, , 5p + q = 2, , 6p From, 6p ⇒6p, , +, , (1), , 3q = 1, (2), (1) ⇒ q = 2 – 5p Substituting in (2) we get, 3(2 – 5p) = 1, - 6 + 15p = 1 ⇒21p = 7 ⇒p =, , Substitute p = in (1),, 5, , + q = 2 ⇒q = 2 - ⇒ q =, , = p⇒, , = ⇒3=x–1⇒x=4, , =q⇒, , = ⇒ 3 = y– 2 ⇒ y= 5, , Example 19:A boat goes 30 km upstream and 44 km downstream in10 hours. In 13, hours, it can go4 0 km u ps t r ea m a nd 5 5 km down-stream. Determine the speed, of the stream and that of the boat in still water., Solution: Let speed of the boat in still water = x km/h and the speed of the stream = y km/h, Then the speed of the boat down stream = (x + y) km/h ªÀÄvÀÄÛ, Speed of the boat in upstram = (x - y) km/h, time =, In the first case, when the boat goes 30 km upstream, let the time taken, in hour be T 1, , P a g e 91 | 159 Available in ykoyyur.blogspot.com

Page 93 :
SSLC Mathematics Solutions – Part -1, , YK, , Then T1 =, Let T2 be the time, in hours, taken by the boat to go 44 km downstream, , Then T2 =, The total time taken (T1 + T2 ) ⇒, , +, , = 10, , (1), , In the second case, in 13 hours it can go 40 km upstream and 55 km downstream we get the equation,, , +, , = 13, , (2), , = p;, , Let, , = q,, , (1) ⇒ 30p + 44q = 10 ⇒ 30P + 44q – 10 = 0, , (3), , (2) ⇒ 40p + 55q = 13⇒40p + 55q – 13 = 0, (4), Here, a = 30 , b = 44, c = -10 and a = 40, b = 55, c = -13, , =, ⇒, , (, , )(, , =, , ) (, , ⇒, , )(, , ), , =(, , =, , ⇒, , =, , ⇒, , =, , ), , (, , ), , =, , (, , ), , (, , ), , =, , =, , p =, , ⇒p=, =, , ⇒q =, ⇒, , ⇒q=, = p⇒, , =q⇒, , = ⇒ x– y= 5, =, , ⇒ x + y = 11, , Adding the equations we get,, 2x = 16 ⇒ x = 8, 8 – y = 5⇒ y = 3, Therefore the speed of the boat = km/h and speed of the stream = 3km/h, , Exercise 3.6, 1., , Solve the following pairs of equations by reducing them to a pair of linear equations, , (i), , Let, , +, , = 2;, , = p and, , +, , =, , = q, , P a g e 92 | 159 Available in ykoyyur.blogspot.com

Page 96 :
SSLC Mathematics Solutions – Part -1, ⇒, , + = 6;, , Let, , =5, , +, , =p; =q, , 6p + 3q = 6, 2p + 4q = 5, Multply equation (2) by 3,, 6p + 12q = 15, Substract (1) from (3),, , (1), (2), (3), , 6p + 12q = 15, 6p + 3q = 6, 9q = 9, ⇒ q=1, Substitute q= 1 in equation (2) we get,, 2p + 4(1) = 5⇒ 2p = 1, ⇒p =, =p⇒, , ⇒ y= 2, , =, , =q⇒ =1⇒x=1, (vii), , +, , Let, , =p;, , =, , ;, =q, , 10p + 2q = 4, 15p - 5q = -2, (1) ⇒ 5p + q = 2, (3) ⇒ q = 2 – 5p, Substitute (4) in (2) we get,, 15p - 5(2-5p) = -2, ⇒15p – 10 + 25p = -2, ⇒40p = 8, ⇒p=, ⇒, Substitute p =, 5, , = −, , -, , (1), (2), (3), (4), , in (3) we get,, , +q=2⇒1 +q=2, , ⇒q = 1, =p⇒, ⇒x+y=5, = q⇒, , =, (5), =1, , ⇒x – y = 1, (6), By adding (5) and (6), x+ y=5, x– y=1, 2x = 6, ⇒ x= 3, Substituting x = 3 in equation (5), we get, P a g e 95 | 159 Available in ykoyyur.blogspot.com, , YK

Page 97 :
SSLC Mathematics Solutions – Part -1, , YK, , 3 + y = 5 ⇒ y = 5 -3 ⇒ y = 2, Therefore the solutions are x = 3, y = 2, (viii), , +, , Let, , =, , =p;, , P+q=, -, , =, , ;, , (, , ), , -, , (, , ), , =, , =q, , ⇒ 4p + 4q = 3, , (1), , ⇒4p – 4q = -1, , (2), , Substract (2) from (1), 4p + 4q = 3, 4p – 4q = -1, 8q = 4, ⇒q = ⇒q =, Substitute q = in (1) we get,, 4p + 4, , = 3 ⇒ 4p + 2 = 3 ⇒4p = 1 ⇒p =, , =p⇒, , =, , ⇒ 3x + y = 4, , (3), , =q⇒, , =, , ⇒ 3x – y = 2, , (4), , By adding (3) and (4), we get, 3x + y = 4, 3x – y = 2, 6x, =6, ⇒ x=1, Substituting x = 1in equation (3),, 3(1) + y = 4 ⇒ y = 4 – 3 ⇒ y = 1, Therefore the solutions are x = 1, y = 1, 2. Formulate the following problems as a pair of equations, and hence find their solutions., (i) Ritu can row downstream 20 km in 2 hours, and upstream 4 km in 2 hours. Find her, speed of rowing in still water and the speed of the current., Let the speed of Ritu in still water = x km/h the speed of the stream = y km/h, The speed of Ritu in upstream = (x - y) km/h, The speed of Ritu in downstream = (x + y) km/h, According to question, 2(x + y) = 20, ⇒ x + y = 10, (1), 2(x - y) = 4, ⇒ x-y=2, (2), By adding equation (1) and (2) ,, x + y = 10, x-y= 2, 2x = 12, ⇒ x= 6, Substituting x = 6 in (1), 6 + y = 10 ⇒ y = 10 – 6 ⇒y = 4, Therefore the speed of Ritu in still water = 6 km/h and the speed of the water = 4 km/h., P a g e 96 | 159 Available in ykoyyur.blogspot.com

Page 98 :
SSLC Mathematics Solutions – Part -1, , YK, , (ii) 2 women and 5 men can together finish an embroidery work in 4 days, while 3, women and 6 men can finish it in 3 days. Find the time taken by 1 woman alone to finish, the work, and also that taken by 1 man alone., Let the time taken by women to finish embroidery work = x days and, the time taken by men = y days, Therefore the work finished by one women in a day = and, the work finished by a man in day = . According to question,, +, , =, , +, , ;, , =, , = p; =q, , Let, , 2p + 5q =, , ⇒ 8p + 20q = 1, , (1), , 3p + 6q =, ⇒9p + 18q = 1, (2), –, (1) ⇒ 8p = 1 – 20q ⇒ p =, Substituting p =, , –, , in (2), , –, , 9, + 18q = 1 ⇒, ⇒9 – 180q + 144q = 8, ⇒-36q = - 1 ⇒ q =, Substituting q =, , –, , in (1),, , = 1 ⇒ 8p +, , 8p + 20, , + 18q = 1, Multiplying by 8, , = 1 ⇒ 8p + = 1, , ⇒ 72p + 5 = 9 ⇒ 72p = 4 ⇒ p =, = p⇒, , =, , =q ⇒, , =, , ⇒ p=, , ⇒x = 18, ⇒y = 36, , Therefore the time taken by a women to finish the work = 18 days and a man = 36 days, (iii) Roohi travels 300 km to her home partly by train and partly by bus. She takes 4, hours if she travels 60 km by train and the remaining by bus. If she travels 100 km by, train and the remaining by bus, she takes 10 minutes longer. Find the speed of the train, and the bus separately., Let the speed of the train = x km/h and the speed of the bus y km/h, According to question,, +, = 4, (1), +, , Let, , =, , = p and, , (2), = q, , 60p + 240q = 4 ⇒15p + 60q = 1, 100p + 200q = ⇒ 600p + 1200q = 25, ⇒24p + 48q = 1, (4), (3) ⇒ 15p = 1 - 60q ⇒ P =, Substitute P =, , in (4) ,, , P a g e 97 | 159 Available in ykoyyur.blogspot.com, , (3)

Page 99 :
SSLC Mathematics Solutions – Part -1, 24, , + 48q = 1, , ⇒, , + 48q = 1, , YK, , Multiplying by 15 ,, , 24 – 1440q + 720q = 15 ⇒ -720q = - 9 ⇒ q =, , Substitute q =, 15p + 60, 15p +, , in (3),, =1, , = 1⇒ 15p = 1 -, , =p⇒, = q⇒, , =, =, , ⇒ 15p =, , ⇒p =, , ⇒ x = 60, ⇒ y = 80, , Therefore the speed of the train = 60 km/h and the speed of the bus = 80 km/h., , Summery:, 1. Two linear equations in the same two variables are called a pair of linear equations in two, variables. The most general form of a pair of linear equations is, a x + b y + c = 0 and a x + b y + c = 0, 2. A pair of linear equations in two variables can be represented, and solved, by the:, (i) graphical method (ii) algebraic method, 3. Graphical Method :, The graph of a pair of linear equations in two variables is represented by, two lines., (i) If the lines intersect at a point, then that point gives the unique solution of the two equations., In this case, the pair of equations is consistent., (ii) If the lines coincide, then there are infinitely many solutions — each point, on the line being a solution. In this case, the pair of equations is dependent, (consistent)., (iii)If the lines are parallel, then the pair of equations has no solution. In this case, the pair of, equations is inconsistent, 4. Algebraic Methods : We have discussed the following methods for finding the solution(s), of a pair of linear equations :, (i) Substitution Method, (ii) Elimination Method, (iii) Cross-multiplication Method, 5. If a pair of linear equations is given by a x + b y + c = 0 and a x + b y + c = 0, the the, following situations can arise :, ≠, In this case, the pair of linear equations is consistent, =, , ≠, , In this case, the pair of linear equations is inconsistent, , =, , =, , In this case, the pair of linear equations is dependent and consistent, , 6. There are several situations which can be mathematically represented by two equations that, are not linear to start with. But we alter them so that they are reduced to a pair of linear, equations, P a g e 98 | 159 Available in ykoyyur.blogspot.com

Page 100 :
SSLC Mathematics Solutions – Part -1, , YK, , Circles, , Non-intersecting Line: The line PQ and the circle have no common, point. In this case, PQ is called a non-intersecting line.PQ is nonintersecting line for the circle of center A, Secant: There are two common points M and N that the line PQ and, the circle have. In this case, we call the line PQ a secant of the circle, of center B, Tangent: There is only one point O which is common to the line PQ, and the circle. In this case, the line is called a tangent to the circle of, center C, 4.2 Tangent to a Circle, Tangent to a circle is a line that intersects the circle at only one point. There is only one, tangent to a circle at a point. The common point of the tangent and the circle is called the, point of contact., , The tangent at any point of a circle is perpendicular to the radius, through the point of contact., , Given:A circle with centre O and tangent XY at a point P., To Prove: OP⟘XY, Consruction: Take any point Q, other than P on the tangent XY, and join OQ, Proof: Hence, Q is a point on the tangent XY, other than the point of contact P. So Q lies, outside the circle.., [∵There is only one point of contact to a tangent], P a g e 99 | 159 Available in ykoyyur.blogspot.com

Page 101 :
SSLC Mathematics Solutions – Part -1, , YK, , Let OQ intersect the circle at R, ∴ OP = OR [∵ Radius of the same circle ], Now, OQ = OR + RQ, ⇒OQ > OR, ⇒OQ> OP [∵OP = OR], Therefore, OP is the shortest distance to the tangent from the center O, ∴ OP⟘XY [∵ Perpendicular distance is always the shortest distance], Remarks :, 1. By theorem above, we can also conclude that at any point on a circle there, can be one and only one tangent., 2. The line containing the radius through the point of contact is also sometimes called the, ‘normal’ to the circle at the point., , Exercise 4.1, 1. How many tangents can a circle have?, , Answer: Infinite, 2. Fill in the blanks :, , i) A tangent to a circle intersects it in, point (s)., Answer: One, (ii) A line intersecting a circle in two points is called a, ., Answer: Secant, iii) A circle can have, parallel tangents at the most., Answer: Two [Note: we can draw only two(pair) parallel tangents each other. But we can, draw infinite parallel pair of tangents], iv) The common point of a tangent to a circle and the circle is called, ., Answer: Point of cantact, 3. A tangent PQ at a point P of a circle of radius 5 cm meets a line through the centre O at, , a point Q so that OQ = 12 cm. Length PQ is :, a), 12 cm, b) 13 cm, c), 8.5 cm, Answer:, , d), , √, , cm, , The line drawn from the point of contact to the center of the circle is perpendicular to the, tangent., ⇒OP ⊥ PQ, In ΔOPQ,, OQ2 = OP2 + PQ2[Pythagoras Theorem], ⇒ (12)2 = 52 + PQ2, ⇒PQ2 = 144 - 25, ⇒PQ2 = 119, ⇒PQ = √119 cm, (d) √, cm, , P a g e 100 | 159 Available in ykoyyur.blogspot.com

Page 102 :
SSLC Mathematics Solutions – Part -1, , YK, , 4. Draw a circle and two lines parallel to a given line such that one is a tangent and the, other, a secant to the circle., AB – A line, PQ – A secant, XY – A tangent, , 4.3 Number of Tangents from a Point on a Circle, Case 1 : There is no tangent to a circle passing through a point lying inside the circle., Case 2 : There is one and only one tangent to a circle passing through a point lying on the circle., Case 3 : There are exactly two tangents to a circle through a point lying outside the circle., , The lengths of tangents drawn from an external point to a, circle are equal., , zÀvÀÛ: PQ and PR are the two tangents drawn from, , an external point P to a circle of center O. JoinOP,, OQ, OR, T Prove: PQ = PR, Proof: In right angle triangle OQP and ORP,, OQ = OR [Radius of the same circle], OP = OP [Common side], ∴ , ∆OQ P ≅∆ ORP [RHS], ∴ , PQ = PR [CPCT], Example 1 : Prove that in two concentric circles, the chord of the larger circle, which, touches the smaller circle, is bisected at the point of contact., We are given two concentric circles C1 and C2 with, centre O and a chord AB of the larger circle C1 which, touches the smaller circle C2 at the point P (see Fig. 4.8)., We need to prove that AP = BP., Let us join OP. Then, AB is a tangent to C2 at Pand OP, is its radius. Therefore, by Theorem 4.1,, Therefore OP⟘AB [From theorem 4.1], Now AB is a chord of the circle C1 and OP⟘AB, Therefore, OP is the bisector of the chord AB, as the perpendicular from the centre bisects, the chord,, ⇒ AP = BP, P a g e 101 | 159 Available in ykoyyur.blogspot.com

Page 104 :
SSLC Mathematics Solutions – Part -1, , YK, , 2. In Fig. 4.11, if TP and TQ are the two tangents to a circle with centre O so that POQ =, 110°, then PTQ is equal to, TP and TQ are the tangents to a circle at P and Q OP and, OQ are radius of the circle at point of contacts P and Q, ∴ OP ⊥ TP and OQ ⊥ TQ, ∠OPT = ∠OQT = 90°, In Quadrilateral POQT,, ∠PTQ + ∠OPT + ∠POQ + ∠OQT = 360°, ⇒ ∠PTQ + 90° + 110° + 90° = 360°, ⇒ ∠PTQ = 70°, ⇒Ans (B) 70°., A), 60, B), 70, C), 80, D), 90, , 3., , If tangents PA and PB from a point P to a circle with centre O are inclined to each other, at angle of 80°, then POA is equal to, OA and OB are the radius drawn at the point of contact of the tangents BP and BQ, ∴ OA ⊥ PA and OB ⊥ PB, ∠OBP = ∠OAP = 90°, In Quadrilateral AOBP,, ∠AOB + ∠OBP + ∠OAP + ∠APB = 360°, ⇒ ∠AOB + 90° + 90° + 80° = 360°, ⇒ ∠AOB = 100°, Now, In ΔOPB and ΔOPA,, AP = BP [Tangents drawn from an external point], OA = OB [Radius of the same circle], OP = OP [Common], ∴ ΔOPB ≅ ΔOPA [SSS congruence rule], ⇒∠POB = ∠POA, ∠AOB = ∠POB + ∠POA, ⇒ 2 ∠POA = ∠AOB, ⇒ ∠POA = 50°, ⇒ (A) 50°, A), 500, B), 600, C), 700, D), 800, 4. Prove that the tangents drawn at the ends of a diameter of a circle are parallel., AB is a diameter. PQ and RS are the tangents drawn, to the circle at point A and B, OA and OB are the radius drawn at point of contact., ∴ OA ⊥ PQ and OB ⊥ RS, ∠OAP = ∠OAQ = ∠OBR = ∠OBS = 90º, In the fig,, ∠OBR = ∠OAQ [Alternate angles ], ∠OBS = ∠OAP [Alternate angles ], ⇒ PQǁ RS, 5. Prove that the perpendicular at the point of contact to the tangent to a circle passes, through the centre., P a g e 103 | 159 Available in ykoyyur.blogspot.com

Page 105 :
SSLC Mathematics Solutions – Part -1, , YK, , AB is the tangent drawn to the circle with radius O, To Prove:The perpendicular at P passes through the center O., If possible,let the perpendicular passing through some other, Point say Q, Join QP and OP, OP is the radius at point of contact AB is the tangent, ∴ OP⟘AB ⇒ ∠OPA = 90 0, But, ∠RPA = 90° (PQ ⊥ AB), ⇒ Which is possible only when points P and Q coinside., ∴ the perpendicular at the point of contact to the tangent to a circle passes through the centre., 6. The length of a tangent from a point A at distance 5 cm from the centre of the circle is 4, cm. Find the radius of the circle, AB is the tangent to the circle at point B. OB is the radius at point of contact, ∴ OB ⊥ AB, OA = 5cm and AB = 4 cm [Given], In ΔABO,, OA2 = AB2 + BO2 [Pythagoras theorem], ⇒ 52 = 4 2 + BO2 ⇒ BO2 = 25 - 16, ⇒ BO2 = 9 ⇒ BO = 3, ∴ Radius = 3 cm., 7. Two concentric circles are of radii 5 cm and 3 cm. Find the length of the chord of the, larger circle which touches the smaller circle., Two concentric circles of radius 5cm and 3cm drawn with, common center O, AB is the chord of circle with radius 5cm such that it touches, the circle of radius 3cm at P, ∴ AB is the tangent to the smaller circle at P, ⇒ OP ⊥ AB, ∴ AP = PB [The perpendicular drawn from the center to the chord bisects the chord], OA2 = AP2 + OP2 [By Pythagoras theorem], ⇒ 52 = AP2 + 3 2 ⇒ AP2 = 25 – 9 ⇒ AP = 4,, AB = 2AP = 2 × 4 = 8 cm, ∴ The length of the chord = 8 cm., 8. A quadrilateral ABCD is drawn to circumscribe a circle (see Fig. 4.12). Prove that, AB + CD = AD + BC, From the figure,, DR = DS [Tangents from the external point D ], (1), AP = AS [Tangents from the external point A ], (2), BP = BQ [Tangents from the external point B ], (3), CR = CQ [Tangents from the external point C ], (4), (1) + (2) + (3) + (4), DR + AP + BP + CR = DS + AS + BQ + CQ, ⇒ (BP + AP) + (DR + CR) = (DS + AS) + (CQ + BQ), ⇒AB + CD = AD + BC, P a g e 104 | 159 Available in ykoyyur.blogspot.com

Page 107 :
SSLC Mathematics Solutions – Part -1, , YK, , Adding all these, we get, DR + CR + BP + AP = DS + CQ + BQ + AS, ⇒ (BP + AP) + (DR + CR) = (DS + AS) + (CQ + BQ), ⇒ AB + CD = AD + BC, (3), Substituting (1) and (2) in (3),, 2AB = 2BC ⇒ AB = BC, From equation (1), (2) and (4),, , 12., , (4), , AB = BC = CD = DA, ∴ ABCD is a Rhombus, A triangle ABC is drawn to circumscribe a circle of radius 4 cm such that the segments, BD and DC into which BC is divided by the point of con tact D ar e of len gth s 8 cm, and 6 cm respectively (see Fig. 4.14). Find the sides AB and AC., In ΔABC,, CF = CD = 6cm [Tangents from an external point], BE = BD = 8cm [Tangents from an external point], AE = AF = x [Tangents from an external point], ⇒a = AB = AE + EB = x + 8, b = BC = BD + DC = 8 + 6 = 14, c= CA = CF + FA = 6 + x, S=, =, =, ⇒ S = 14 + x, Area of ΔABC =, ( − )( − )( − ), = 14 + [14 + − ( + 8)](14 + − 14)[14 + − (6 + )], = (14 + ) [14 + − − 8](14 + − 14)[14 + − 6 − ], = (14 + ) (6)( )(8), = (14 + ) 48 cm2, (1), Similarlly, Area of ΔABC= Area of ΔOCB+ Area of ΔOBA+ Area of ΔOAC, = BC.OD + AB.OE + AC.OF, = (14x4) + (8+x)4 + (6+x)4 = 28 + 16 + 2 + 12 + 2, = (56 + 4 )cm2, From (1) and (2),, , (2), , (14 + ) 48 = 56 + 4, 48x (14 + x) = (56 + 4x)2 [ Squaring on both sides], ⇒ 48x =, , [ (, , )], , ⇒ 48x = 16 (14 + x) ⇒ 48x = 224 + 16x ⇒ 32x = 224 ⇒ x = 7 cm, Therefore, AB = x + 8 = 7 + 8 = 15 cm, CA = 6 + x = 6 + 7 = 13 cm, 13. Prove that opposite sides of a quadrilateral, circumscribing a circle subtend supplementary angles, at the centre of the circle., , P a g e 106 | 159 Available in ykoyyur.blogspot.com

Page 108 :
SSLC Mathematics Solutions – Part -1, , YK, , Given: ABCD is a quadrilateral circumscribing a circle, with center O. Let the circle touches the quadrilateral at, points P,Q,R and S, To Prove:∠AOB + ∠COD = 1800 and ∠AOD + ∠BOC = 1800, Construction: Join OP, OQ, OR and OS., Proof: The tangents drawn from an external point to the, circle substend equal angle at the center., ⇒∠1 = ∠2; ∠3 = ∠4; ∠5 = ∠6; ∠7 = ∠8, But,, ∠1 + ∠2 + ∠3 + ∠4 + ∠5 + ∠6 + ∠7 +∠8 = 360º, (∠1 + ∠2) + (∠3 + ∠4) + (∠5 + ∠6) + (∠7 +∠8) = 360º, ⇒ 2(∠2 + ∠3) + 2(∠6 + ∠7) = 360º, ⇒ (∠2 + ∠3) + (∠6 + ∠7) = 180º, ⇒ ∠AOB + ∠COD = 1800, Similarlly, ∠AOD + ∠BOC = 1800, ∴ Opposite sides of a quadrilateral circumscribing a circle subtend supplementary, angles at the centre of the circle., , Summary, 1. The tangent to a circle is perpendicular to the radius through the point of contact., 2. The length of the tangents from an external point to the circle are equal., , P a g e 107 | 159 Available in ykoyyur.blogspot.com

Page 109 :
SSLC Mathematics Solutions – Part -1, , YK, , Area Related to, circles, 5.2 Perimeter and Area of a Circle — A Review, The distance covered by travelling once around a circle is its perimeter, usually called its, circumference. You also know from your earlier classes, that circumference of a circle bears, a constant ratio with its diameter. This constant ratio is denoted by the Greek letter, (read, as ‘pi’). In other words,, , The cost of fencing a circular field at the rate of R s 24 per metre is Rs 5280. The field, is to be ploughed at the rate of R s 0.50 per m2. Find the cost of ploughing the field. (Take, =, ), Solution:Length of the fence (in metres) =, , =, , = 220 «ÄÃ., , So, circumference of the field = 220 m. Therefore, if r metres is the radius of the field,, then, 2 r = 220 Or 2 x, , x r = 220 ⇒ r =, , Therefore, area of the field = πr =, , = 35m, , x 352 = (22 x 5 x 35)m2, , Total cost of ploughing the field at the rate of 0.50/sqm = (22 x 5 x 35) x 0.5 = gÀÆ 1925, , Exercise 5.1, [Unless stated otherwise, use, , =, , ], , 1. The radii of two circles are 19 cm and 9 cm respectively.Find the radius of the circle, which has circumference equal to the sum of the circumferences of the two circles., Let the required radius = R. Therefore the circumference C = 2πR, The circumference of the circle of radius 19 cm = 2π × 19 = 38π cm, The circumference of the circle of radius = 2π × 9 = 18π cm, The sum of the circumference of two circles = 38π + 18π = 56π cm, ⇒ 2πR = 56π cm [According to question] ⇒ 2R = 56 cm ⇒ R = 28 cm, 2. The radii of two circles are 8 cm and 6 cm respectively. Find the radius of the circle, having area equal to the sum of the areas of the two circles., , P a g e 108 | 159 Available in ykoyyur.blogspot.com

Page 110 :
SSLC Mathematics Solutions – Part -1, , YK, , Let the required radius = R. Therefore the area = πR2, The area of the circle of radius 8 cm = π × 82 = 64π cm2, The area of the circle of radius 6 cm = π × 62 = 36π cm2, The sum of the areas of two circles = 64π cm2 + 36π cm2 = 100π cm2, According to question,, πR2 = 100π cm2⇒ R2 = 100cm2 ⇒ R2 = 100 cm2 ⇒ R = 10 cm, 3. Fig. 5.3 depicts an archery target marked with its five scoring regions from the centre, outwards as Gold, Red, Blue, Black and White. The diameter of the region representing, Gold score is 21 cm and each of the other bands is 10.5 cm wide.Find the area of each of, the five scoring regions., The diameter of the Golden colour Circle = 21 cm, st, 2 nd circle, 3rd circle, 4th circle, 5th circle, 1 circle, r2 = 21 cm, r3 = 31.5, r4 = 42, r5 = 52.5, r1 = 10.5 cm, 2, 2, 2, 2, A1 = π r 1, A2 = π r2, A3 = π r 3, A4 = π r 4, A5 = π r 5 2, π(21)2, π(31.5)2, π(42)2, π(52.5)2, π (10.5)2, 1386 cm2, 3118.5 cm2, 5544 cm2, 8662.5 cm2, 346.5 cm2, Area of Golden colour = π r12 = π (10.5)2 = 346.5 cm2, Area of Red colour = [Area of 2 nd – Area of 1 st ], = 1386 - 346.5 cm2 = 1039.5 cm2, Area of blue colour = [Area of 3rd – Area of 2 nd ], = 3118.5 - 1386 cm2 = 1732.5 cm2, Area of black colour = [Area of 4th – Area of 3 rd ], = 5544 - 3118.5 cm2 = 2425.5 cm2, Area of white colour = [Area of 5th – Area of 4th], = 8662.5 cm2 - 5544 cm2 = 3118.5cm2, 4. The wheels of a car are of diameter 80 cm each. How many complete revolutions does, each wheel make in 10 minutes when the car is travelling at a speed of 66 km per hour?, The diameter of the wheels of a car = 80 cm, Circumference of the wheel C = 2πr = 2r × π = 80 π cm, The Car traveled a distance in 10 minutes = (66 × 1000 × 100 × 10)/60 = 110000 cm, ಚ ದ ದೂರ, Therefore no of revolution =, =, =, = 4375, 5. Tick the correct answer in the following and justify your choice : If the perimeter and the, area of a circle are numerically equal, then the radius of the circle is, A) 2 Units B) Units C) 4 Units D) 7 Units, Radius of the circle = r, ∴ Circumference(Perimeter) = 2πr, According to question,, Perimeter = Area, , ∴ Area = π r2, , 2πr = π r2⇒ 2 = r, ∴ A) 2 Units, , P a g e 109 | 159 Available in ykoyyur.blogspot.com

Page 111 :
SSLC Mathematics Solutions – Part -1, , YK, , 5.3 Areas of Sector and Segment of a Circle, The portion (or part) of the circular region enclosed by two radii and the corresponding arc is, called a sector of the circle and the portion (or part) of the circular region enclosed between, a chord and the corresponding arc is called a segment of the circle., , some relations (or formulae) to calculate their areas., Let OAPB be a sector of a circle with centre O and radius r, (see Fig. 5.6). Let the degree measure of ∠AOB be θ ,, If the angle at the center is 3600, then the area of the sector =, So, when the degr ee measure of the a ngle at t he, Centre is 1, area of the sector =, Therefore, when the degree measure of the angle at the centre is θ,, xθ⇒, , Area of the sector =, , Area of the sector of angle θ =, , θ, , x, x, , Length of the arc of a sector of angle θ =, Areaof SegmentAPB, , x, , Area of OAPB Sector – Area of ∆OAB, r2 - Area of Minor sectorOAPB, , Area of OAQB Major sector, , r2 – Area of APB Minor segment, , Area of AQB Major segment, , Example 2 : Find the area of the sector of a circle with radius 4 cm and of angle 30°., Also, find the area of the corresponding major sector (Use = 3.14), Solution: Given sector is OAPB., Area of the sector OAPB =, ⇒, , x 3.14 x 4 x 4 =, , ., , x, ≈ 4.19 cm2, , Area of the corresponding major sector, = r2 - Area of sector OAPB = (3.14 x 16 - 4.19) cm2≈ 46.1 cm2, Alternate Method:, Area of the corresponding major sector =, =, , 360−30, , 360−θ, , x, , x 3.14 x 4 x 4 = 46.05 ≈ 46.1 cm2, , P a g e 110 | 159 Available in ykoyyur.blogspot.com

Page 112 :
SSLC Mathematics Solutions – Part -1, , YK, , Example 3 : Find the area of the segment AYB shown in Fig. 5.9, if radius of the, circle is 21 cm and ∠AOB = 120 0 (, =, ), Solution: Area of the segment, =Area of sector OAYB – Area of ∆OAB ------- (1), Area of the sector =, =, , 120, , x, , θ, , x, , x 21 x 21 = 462cm2, , (2), , To find the area of ∆OAB, draw OM⟘AB as shown in fig.5.10, Note that OA = OB, Therefore, by RHS congruence ∆AMO ≅ ∆BMO, So, M is the mid-point of AB and ∠AOM = ∠BOM = 600, In ∆OAM,, , = Cos600 ⇒, , =, , In ∆OAM,, , = Sin600 ⇒, , =, , ⇒ OM =, √, , cm, √, , ⇒ AM =, , cm, , ⇒AB = 2AM ⇒ 21√3cm, ∴ Area of ∆OAB =, , x 21√3 x, , x AB x OM =, , Are of the segment = 462 -, , √, , √, , =, , √, , =, =, , cm2, , (3), , (88 - 21√3)cm2, , Exercise 5.2, [Unless stated, otherwise use = ], 1. Find the area of a sector of a circle with radius 6 cm if angle, of the sector is 60°., Area of the sector of angle θ =, ×π r2, °, Area of the sector of angle 600 =, = ×6x6 x, , =, , °, , ×π r2 cm2, , cm2, , 2. Find the area of a quadrant of a circle whose circumference is 22 cm, Quadrant of a circle = Angle of sector 900, Circumference C = 2πr = 22 cm, Radius r = cm =, = cm, Area of the sector of angle θ =, , °, , ×π r2, , Area of the sector of angle 90° =, ×π r2 = × x x = cm2, °, 3. The length of the minute hand of a clock is 14 cm., Find the area swept by the minute hand in 5 minutes., The minute hand is the radius of the circle. ⇒ Radius(r) = 14 cm, The angle of rotation formed by minute hand in 1 hour = 360°, °, ∴ The angle of rotation in 5 minutes =, × 5 = 30°, Area of the sector of angle θ =, , °, , ×π r2, , ∴ Area of the sector of angle 30 0 =, =, , ×22 x 7 =, , cm, , °, , ×, , x 14 x 14=, , 2, , P a g e 111 | 159 Available in ykoyyur.blogspot.com, , ×, , x 14 x 14

Page 113 :
SSLC Mathematics Solutions – Part -1, , YK, , 4. A chord of a circle of radius 10 cm subtends a right angle at the centre. Find the area of, the corresponding : (i) minor segment (ii) major sector. (Use = 3.14), Radius of the circle = 10 cm, The angle of the Major sector = 360° - 90° = 270°, Area of the major sector =, , °, , ×π r2 cm2, , = × 3.14 x10 x 10 = 75 x 3.14 cm2 = 235.5 cm2, In right angle ΔAOB , OA = 10 cm, OB = 10 cm, Area of ΔAOB = × OA × OB= ×10 × 10 = 50 cm2 --- (1), The angle of the Minor sector = 90°, Area of the minor sector =, , °, , ×π r2 cm2, , = × 3.14 x10 x 10 = 25 x 3.14 cm2 = 25 × 3.14 cm2 = 78.5 cm2 -------- (2), Area of minor segment = (2) - (1) = 78.5 cm2 - 50 cm2 = 28.5 cm2, 5. In a circle of radius 21 cm, an arc subtends an angle of 60° at the centre. Find:, (i) the length of the arc (ii) area of the sector formed by the arc, (iii) area of the segment formed by the corresponding chord, Radius of the circle = 21 cm, (i) The length of the Arc AB =, Arc AB =, , °, , ×2x, , x 21 =, , °, , × 2πr, , × 2 x 22 x 3 = 22cm, , (ii) The angle formed by arc AB = 60°, Area of the sector of angle 60 0 = ° ×π r2 cm2, =, , °, , x, , x 21x21 cm2= x 22x 3 x21 cm2= x 22x21 cm2, , = 11x21 cm2 = 231 cm2, √, , √, , √, , (iii) The area of the equilateral ΔAOB = x (OA)2 = x (21)2 =, cm2, Hence the required area = Area of the sector formed by the Arc - area of ΔAOB, √, , =, −, cm2, 6. A chord of a circle of radius 15 cm subtends an angle of 60° at the centre. Find the areas, of the corresponding minor and major segments of the circle. (Use = √ = 1.73), Radius of the circle = 15 cm, In triangle ΔAOB, ∠AOB and ∠A = ∠B = 600 [∵OA = OB = 15cm], ∴ ΔAOB is an equilateral triangle., The area of ΔAOB =, =, , ., , √, , x (OA)2 =, , √, , x (15)2 =, , √, , cm2, , cm2 = 97.3 cm2, , The angle formed by the arc AB = 60°, ∴ The area of the sector formed by the arc AB =, , °, , ×π r2 cm2, , = ° x (3.14)x 15x15 cm2 = x 3.14 x 5x15 cm2 = 1.57 x 75 cm2 = 117.75 cm2, Area of the minor segment = Area of the sector formed by the arc AB – Area of ΔAOB, = 117.75 - 97.3 = 20.4 cm2, Area of the major segment = Area of the circle – Area of minor segment, P a g e 112 | 159 Available in ykoyyur.blogspot.com

Page 114 :
SSLC Mathematics Solutions – Part -1, , YK, , = π r2 - 20.4 cm2 = 3.14 x 15x15 - 20.4 = 3.14 x 225 – 20.4, = 706.5 – 20.4 = 686.1cm2, 7. A chord of a circle of radius 12 cm subtends an angle of 120° at the centre. Find the, area of the corresponding segment of the circle. (Use = 3.14 and √ = 1.73)., Radius of the circle(r) = 12 cm, Draw AB ⟘ OD ⇒ OD bisects AB, ⇒∠A = 180° - (90° + 60°) = 30°, cos 30° =, , ⇒, , √, , ⇒ AD = 6√3 cm, , =, , ⇒ AB = 2 × AD = 12√3 cm, sin 30° =, , ⇒, , ⇒ OD = 6 cm, , =, , The area of ΔAOB = × AB × OD, =, , x 12√3 x 6 cm2 = 36√3 cm = 36 × 1.73 = 62.28 cm2, , The angle of minor sector = 120°, °, ∴ Area of the minor sector =, ×π r2 cm2, °, , °, , 2, , =, x 3.14 x 12 x 12 cm = x 3.14 x 12 x 12 cm2, °, = 3.14 x 4 x 12 cm2 = 3.14 x 48 cm2 = 150.72 cm2, ∴ Area of the minor segment = Area of the minor sector – Area of ΔAOB, = 150.72 cm2 - 62.28 cm2 = 88.44 cm2, 8. A horse is tied to a peg at one corner of a square shaped grass field of side 15 m by, means of a 5 m long rope (see Fig. 5.11). Find, (i) The area of that part of the field in which the horse can graze, (ii) The increase in the grazing area if the rope were10 m long instead of 5 m. (Use = 3.14), Given, the side of the square = 15 m, The length of the rope [Radius of the arc(r)] = 5 m, The radius of the field in which the horse can graze = 5 m., (i) Area of the field graze by the horse, [Horse is tied at the corner of the square.So, it graze only, quadrant of the circle of radius 5m], ., , ., , =, =, =, = 19.625 m2, (ii) The length of the rope is 10m then, the area graze, ., , by the horse =, =, =, = 78.5 m2, Therefore increase in grazing area, = 78.5 m2 - 19.625 m2 = 58.875 m2, 9. A brooch is made with silver wire in the form of a circle with diameter 35 mm. The wire, is also used in making 5 diameters which divide the circle into 10 equal sectors as shown, in Fig. 5.12. Find :, (i) the total length of the silver wire required, (ii) the area of each sector of the brooch., Number of diameters = 5; Legnth of the diameter = 35 mm, ∴ Radius (r) = 35/2 mm, (i) The total lenth of wire required, P a g e 113 | 159 Available in ykoyyur.blogspot.com

Page 115 :
SSLC Mathematics Solutions – Part -1, , YK, , = Perimeter of the brooch + length of 5 diameter, = 2π r + (5×35) mm, = (2 × × ) + 175 mm = 110 + 175 mm = 185 mm, (ii) Number of sectors = 10, Therefore area of each sector =, =, , =, , =, , =, , mm2, , 10. An umbrella has 8 ribs which are equally spaced (see Fig. 5.13). Assuming umbrella to, be a flat circle of radius 45 cm, find the area between the two consecutive ribs of the, umbrella., , Total ribs in the umbrella = 8, The radius of the umbrella when it to be flat = 45 cm, The area between the two consecutive ribs =, =, , =, , =, , cm2 = 795.5 cm2, , =, , 11. A car has two wipers which do not overlap. Each wiper has a blade of length 25 cm, sweeping through an angle of 115°. Find the total area cleaned at each sweep of the blades., The angle of the sector formed by the wiper = 115°, Radius of the sector = length of the wiper = 25 cm, °, Area of the sector formed by the wiper =, ×π r2 cm2, =, =, , °, °, , ×, , °, , ×, , x 25 x 25 cm2, x 625 cm2 =, , ×, , x 625 cm2 =, , cm2, , The total area coveed by blades of two wipers, =2×, cm2 =, = 1254.96 cm2, 12. To warn ships for underwater rocks, a lighthouse spreads, a red coloured light over a sector of angle 80° to a distance, of 16.5 km. Find the area of the sea over which the ships are, warned. (Use = 3.14), Let the lighthouse be at O, Radius of the sector = length of the beam r = 16.5 km, Angle of the sector formed by the beam = 80°, The area of the sector which light spreads = Area of the sector =, =, , ×3.14 x 16.5x16.5km2 =, , ×3.14 x 272.25km2 = 189.97 km2, , P a g e 114 | 159 Available in ykoyyur.blogspot.com, , °, °, , ×π r2 km2

Page 116 :
SSLC Mathematics Solutions – Part -1, , YK, , 13. A round table cover has six equal designs as shown in Fig. 12.14. If the radius of the cover, is 28 cm, find the cost of making the designs at th e rate of Rs 0.35 per cm2 0.35 per, cm2 (Use √ = 1.7)., The number of equal designs = 6; The radius of the cover = 28 cm, Making Cost of the design = gÀÆ 0.35 / cm2, °, , The angle of each sector =, = 60°, ΔAOB AiÀÄ°è OA = OB [Radius of the same circle], ∴ ∠A = ∠B = 600, ∴Area of the equilateral ΔAOB =, =, , √, , √, , x (OA)2, , x (28)2 = 1.7x 7 x 28 = 333.2 cm2, °, , Area of the sector OACB =, , °, , ×π r2 cm2, , = × x 282 cm2 = ×22x 4x28 cm2, = ×22x 2x28 cm2 = 410.67cm2, Area of the design = Area of the sector OACB - Area of the ΔAOB, = 410.67 cm2 - 333.2 cm2 = 77.47 cm2, ∴ The total area of 6 designs = 6 × 77.47 cm2 = 464.82 cm2, ∴ Total cost of making designs = 464.76 cm2 × gÀÆ 0.35 /cm2 = Rs 162.68, 14. Tick the correct answer in the following :, Area of a sector of angle p (in degrees) of a circle with radius R is, A), , x 2πr, , B), , x 2πr, , C), , x 2πR, , The area of the sector of angle p =, Answer (D) x 2, , °, °, , D), , x 2πR, , ×π R 2 cm2 =, , °, , ×π R 2 x =, , x 2πR, , 5.4 Areas of Combinations of Plane Figures, In Fig. 5.15, two circular flower beds have been shown on two sides of a square lawn, ABCD of side 56 m. If the centre of each circular flower bed is the point of intersection, O of the diagonals of the square lawn, find the sum of the areas of the lawn and the, flower beds., Solution: Area of the square lawn = 56 x 56 m2, (1), Let The radius = OA = OB = x m, Therefore, x2 + x2 = 562 [By Pythagoras theorem OA2 + OB2 = AB2], ⇒2x2 = 56 x 56, ⇒x2 = 56 x 28, Now, Area of the sector OAB, =, , x πx =, , x, , x 28 x 56 [ From eqn (2)], , (2), (3), , Total Area = [Area of sector OAB + Area of sector ODC + Area of ∆OAD + Area of ∆OBC], =, , x, , x28x56+, , x, , x28x56 + x56x56+ x56x56, , = 22x56+ 22x56 + 14x56+14x56, = 56(22+ 22 + 14+14) = 56(22+ 22 + 14+14) =56 x72 = 4032m2, , P a g e 115 | 159 Available in ykoyyur.blogspot.com

Page 118 :
SSLC Mathematics Solutions – Part -1, , YK, , 2. Find the area of the shaded region in Fig. 5.20, if radii of the two concentric circles with, centre O are 7 cm and 14 cm respectively and AOC = 40°., Radius of the inner circle = 7 cm, Radius of the outer circle = 14 cm, The angle of the sector = 40°, °, Area of the sector OAC = ° ×π r2 cm2, = x, , x 142 cm2 = x 22 x 2x14 cm2 =, °, , Area OBD = Area of the sector =, = x, , °, , cm2, , ×π r2 cm2, , x 72 cm2 = x 22 x 7 cm2=, , cm2, , ∴ Area of shaded region, = Area of the sector OAC - Area of sector OBD, =, −, cm2 =, cm2 =, cm2, 3. Find the area of the shaded region in Fig. 5.21, if ABCD is a square of side 14 cm and, APD and BPC are semicircles., Side of the square = 14 cm, Diameter of the semi circle = 14 cm, ∴ Radius of the semi circle = 7 cm, Area of the square = 14 × 14 = 196 cm2, Area of the semi circle =, , =, , =, , = 77 cm2, , Area of two semicircle = 2 × 77 cm2 = 154 cm2, ∴ Area of shaded region = 196 cm2 - 154 cm2 = 42 cm2, 4. Find the area of the shaded region in Fig. 5.22, where a circular arc of radius 6 cm has, been drawn with vertex O of an equilateral triangle OAB of side 12 cm as centre., OAB is a equilateral triangle, Therefore each angle = 60°., Radius of the circle = 6 cm., Side of the triangle = 12 cm., Area of the equilateral triangle =, =, , √, , (12)2 = √3 x 3x12 =, , √, , Area of the circle = π R2 =, , √, , cm2, , × 62 =, , The area of the sector of angle 60° =, =, , ×, , x 62 cm2 =, , (OA)2, , cm2 =, , cm2 =, °, °, , cm2, , ×π r2 cm2, , cm2, , ∴ Area of the shaded region, = Area of equilateral triangle + Area of the circle – Area of the sector, =, +, −, cm2 =, cm2, √, √ +, 5. From each corner of a square of side 4 cm a quadrant of a circle of radius 1 cm is cut and, also a circle of diameter 2 cm is cut as shown in Fig. 5.23. Find the area of the remaining, portion of the square., The side of the square = 4 cm; Radius of the circle = 1 cm, P a g e 117 | 159 Available in ykoyyur.blogspot.com

Page 119 :
SSLC Mathematics Solutions – Part -1, , YK, , Area of the square = (Side)2 = 42 = 16 cm2, cm2 =, , Area of each quadrant =, , cm2 =, , ∴ Area of four quadrant = 4 ×, , cm2, , Area of the circle = π R2 cm2 = × 12 =, Area of the square = Side2 = 4 2 = 16cm2, +, , cm2, , =, , cm2, , cm2, , cm2 =, , ∴ Area of shaded region = Area of square – [Area of four quadrants+ area of circle], = 16 −, +, cm2 =, cm2 = cm2, 6. In a circular table cover of radius 32 cm, a design is formed leaving an equilateral, triangle ABC in the middle as shown in Fig. 5.24. Find the area of the design., Radius of the circle = 32 cm, AD is the median drawn through the center O ⇒ BD =, ∴ Radius of the circle AO = AD[ AD is the median], ⇒ AD = 32 cm ⇒ AD = 48 cm, In triangle ΔADB,, AB2 = AD2 + BD2 [By Pythagoras theorem], ⇒ AB2 = 48 2 +, ⇒, , 2, , ⇒ AB2 = 2304 +, , = 2304 ⇒ AB2 = 3072 ⇒ AB = 32√ cm, , Area of ΔABC =, , √, , (AB)2 =, , Area of the circle = π R2 =, , √, , (32√3)2 = 768√ cm2, cm2, , × 32 × 32 =, , ∴Area of the design = Area of the circle - Area of ΔABC, =, −, √ cm2, 7. In Fig. 5.25, ABCD is a square of side 14 cm. With centres A, B, C and D, four circles are, drawn such that each circle touch externally two of the remaining three circles. Find the, area of the shaded region., Side of the Square = 14 cm, ∴ Radius of each circle = = 7 cm, Area of square ABCD = 142 = 196 cm2, Area of the quadrant =, , cm2 =, , ∴ Area of four quadrant = 4×, , =, , cm2 =, , cm2, , cm2 = 154 cm2, , ∴ Area of shaded region, = Area of the square ABCD - 4 Area of four quadrant, = 196 cm2 - 154 cm2= 42 cm2, , P a g e 118 | 159 Available in ykoyyur.blogspot.com

Page 120 :
SSLC Mathematics Solutions – Part -1, , YK, , 8. Fig. 5.26 depicts a racing track whose left and right ends are semicircular., The distance between the two inner, parallel line segments is 60 m and they are, each 106 m long. If the track is 10 m wide,, find :, (i) The distance around the track along its, inner edge, (ii) The area of the track., , Width of the track = 10 m, Distance between parallel lines DE = CF = 60 m, Length of each parallel line = 106 m, Radius of inner circle r = OD = O'C = = 30 m, Radius of outer circle R = OA = O'B = 30 + 10 m = 40 m, AB = CD = EF = GH = 106 m, (i) The distance around the track along its inner edge, = CD + EF + 2 × (Circumference of inner semi-circle), = 106 + 106 + (2 × πr) m = 212 + (2 × × 30) m = 212 +, (ii) Area of the running track, , m=, , m, , = Area ABCD + Area EFGH + 2 xArea of outer semi-circle - 2 x Inner semi-circle, = (AB × CD) + (EF × GH) + 2 ×, , -2×, , m2, , = (106 × 10) + (106 × 10) + 2 × (R2 -r2) m2 = 1060 + 1060 +, , × 700 m2, , = [1060 + 1060 +( 22 × 100)] m2 = [2120 +2200] m2 = 4320 m2, 9. In Fig. 5.27, AB and CD are two diameters of a circle (with, centre O) perpendicular to each other and OD i s t h e d i am, et er of t h e s m a l l er ci r cl e. I f OA = 7 cm, find the area, of the shaded region., Radius of the greater circle R = 7 cm, Radius of the smaller circle r = cm, Height of ΔBCA = OC = 7 cm; Base of ΔBCA = AB = 14 cm, Area of ΔBCA = × AB × OC = × 7 × 14 = 49 cm2, Area of greater circle = πR2 =, , × 72 = 154 cm2, , P a g e 119 | 159 Available in ykoyyur.blogspot.com

Page 121 :
SSLC Mathematics Solutions – Part -1, Area of greater semi-circle =, , cm2 = 77 cm2, , Area of smaller circle = πr2 =, , × × =, , YK, , cm2, , Area of shaded aregion, = Area of greater semi-circle - Area of ΔBCA + Area of smaller circle, = 77 – 49 +, cm2 =, cm2 =, cm2 = 66.5 cm2, 10. The area of an equilateral triangleABC is 17320.5 cm2.With each vertex of the triangle as, centre, a circle is drawn with radius equal to half the length of the side of the triangle, (see Fig. 5.28). Find the area of t h e s h a d ed r eg i on . ( Use = 3 . 1 4 a n d = 3.14 and, √ = 1.73205), ABC is an equilateral triangle ∴ ∠A = ∠B = ∠C = 60°, √, , Area of ΔABC = 17320.5 cm2 ⇒, ⇒ AB2 = 17320.5 ×, , ., , Radius of the circle =, , × (AB)2 = 17320.5, , ⇒ AB2 = 4 × 10 4 ⇒ AB = 200 cm, cm = 100 cm, , Area of three equal sector of angle 600 =3x, , °, °, , ×π r2 cm2, , =3x ×3.14 x 1002 cm2 = ×3.14 x 1002 cm2 =, , cm2 = 15700 cm2, , Area of Shaded region =Area of ΔABC - Area of three equal sector, = (17320.5 – 15700) cm2 = 1620.5 cm2, 11. On a square handkerchief, nine circular designs each of radius 7 cm are made, (see Fig. 5.29). Find the area of the remaining portion of the handkerchief., Number of circles = 9; Radius of each circle = 7 cm, There are three circles touch each other, ∴ Side of the square = 3 × diameter of the circle = 3 × 14 = 42 cm, Area of the square = 42 × 42 cm2 = 1764 cm2, Area of 9 equal circle = 9π r2 = 9x, × 7 × 7 = 1386 cm2, The area of remaing part of the handkerchief, = Area of the square - Area of 9 equal circle = 1764 - 1386 = 378 cm2, 12. In Fig. 5.30, OACB is a quadrant of a circle with centre O and radius 3.5 cm. If OD = 2 cm,, find the area of the, i) quadrant OACB ii) shaded region., Radius of the quadrant of the circle = 3.5 cm = cm, (i) Area of OACB quadrant =, , cm2 =, , cm2=, , cm2, , (ii) Area of ∆BOD = × × 2 cm2= cm2, Area of shaded region, = Area of OACB – Area of ∆ BOD, =, − cm2=, −, cm2 =, , cm2 = 6.125 cm2, , 13. In Fig. 5.31, a square OABC is inscribed in a quadrant OPBQ. If OA = 20 cm, find the area, of the shaded region. (Use = 3.14), Side of the square = OA = AB = 20 cm, P a g e 120 | 159 Available in ykoyyur.blogspot.com

Page 122 :
SSLC Mathematics Solutions – Part -1, , YK, , Radius of the quadrant of the circle = OB, OAB is a right angle triangle, ∴ in right angle ΔOAB,, OB2 = AB2 + OA2 [By Pythagoras theorem ], ⇒ OB2 = 20 2 + 202⇒ OB2 = 400 + 400, ⇒ OB2 = 800⇒ OB = 20√2 cm, cm2, , The area of the quadrant of circle =, ., , ., , √, , =, cm2 =, cm2 = 3.14 x 200 cm2 = 628 cm2, ZËPÀzÀ «¹ÛÃtð = 20 × 20 = 400 cm2, Area of shaded region, = Area of quadrant of circle - Area of the square = 628 - 400 cm2 = 228 cm2, 14. AB and CD are respectively arcs of two concentric circles of radii 21 cm and 7 cm and, centre O (see Fig. 5.32). If AOB = 30°, find the area of the shaded region, Radius of the greater circle R = 21 cm and radius of smaller circle r = 7 cm, The angle formed by two concentric are = 30°, °, Area of outer sector = ° ×π r2 cm2, =, , x 21x21 cm2 = x 22 x 3 x7 cm2, , x, , = x 11 x 3 x7 cm2 =, , cm2, °, , Area of inner sector =, =, , °, , ×π r2 cm2, , x7x7 cm2 = x 11 x7 cm2 =, , x, , cm2, , Area of shaded region, = Area of outer sector - Area of inner sector, =, , −, , cm2 =, , cm2 =, , −, , cm2 =, , cm2, , 15. In Fig. 5.33, ABC is a quadrant of a circle of radius 14 cm and a semicircle is drawn with, BC as diameter. Find the area of the shaded region., The radius of quadrant ABC of circle = 14 cm, AB = AC = 14 cm, BC is the diameter of semi circle, Now, ABC is a right angle triangle, ∴BC2 = AB2 + AC2 [Pythgoras theorem], ⇒ BC2 = 14 2 + 142 ⇒ BC = 14√2 cm, Radius semi circle =, , √, , cm = 7√2 cm, , Area of ΔABC = × 14 × 14 cm2 = 7 × 14 × 14 = 98 cm2, cm2 =, , The area of the quadrant of circle =, Area of semi circle =, , =, , √, , √, , cm2 = 154 cm2, , = 154 cm2, , Area of shaded region, = Area of semi circle + Area of ΔABC- Area of quadrant of circle, P a g e 121 | 159 Available in ykoyyur.blogspot.com

Page 123 :
SSLC Mathematics Solutions – Part -1, , YK, , = 154 + 98 - 154 cm2 = 98 cm2, 16. Calculate the area of the designed region in Fig. 5.34 common between the two, quadrants of circles of radius 8 cm each., AB = BC = CD = AD = 8 cm, Area of ΔABC = Area of ΔADC = x 8 x 8 = 32 cm2, Area of Quadrant AECB = Area of quadrant AFCD, cm2 =, , =, , =, , cm2, , Area of shaded region, = (Area of quadrant AECB – Area ofΔABC), + (Area of quadrant AFCD – Area of ΔADC), =, − 32 +, − 32 cm2, =2x, =2x, , − 32 cm2 = 2 x, cm2 =, , cm2, , cm2, , Summary:, 1., , Circumference of the circle = 2πr, , 2., 3., , Area of the circle = πr, The radius of the circle r the angle measure with θ, Then the Length of the Arc of the sector =, x 2πr, The radius of the circle r the angle measure with θ, Then the area of the sector =, x πr, Area of segment of a circle = Area of the corresponding sector - Area of the, corresponding triangle., , 4., 5., , P a g e 122 | 159 Available in ykoyyur.blogspot.com

Page 124 :
SSLC Mathematics Solutions – Part -1, , 6, , YK, , Constructions, , 6.2 Division of a Line Segment, Construction 6.1: To divide a line segment in a given ratio., Divede a line segment AB in the ratio m:n, Example: Devide the line segment AB in the ratio 3:2, , Step-1: Draw any ray AX, making an acute angle with AB, (Can draw above or below the given line), , Step-2: Locate 5 (= m + n) points A1, A2, A3, A4 and A5 on AX so that AA1 = A1 A2 =, A2 A3 = A3 A4 = A4 A5, Step-3: Join BA5, Step-4: Through the point A3 (m = 3), draw a line parallel to A5B (by making an angle, equal to AA5 B) at A3 intersecting AB at the point C (see Fig.). Then, AC : CB = 3 : 2, Justification:, A3CǁA5B ⇒, , =, , [Basic proportionality theorem]⇒, , Now AC : CB = 3 : 2, , Alternate Method:, Step 1: Draw any ray AX making an, acute angle with AB ., Step 2: Draw a ray BY parallel to AX by, making ∠ABY equal to ∠BAX, Step 3: Locate the points A1, A2, A3 (m, = 3) on AX and B1, B2 (n = 2) on BY, such that AA1 = A1A2 = A2 A3 = BB1, = B1 B2, Step 4: Join A3B2 . Let it intersect AB at, a point C, , P a g e 123 | 159 Available in ykoyyur.blogspot.com, , =, , = ⇒ 3:2

Page 125 :
SSLC Mathematics Solutions – Part -1, , YK, , Justification:, In ∆ AA3C and ∆ BB2C ∠ AC A3 = BC B2 ( Vertically opposite angles), ∠ CAA3 = CBB2 (Alternate angles), ∆ AA3C ~ ∆ BB2C ( AA similarity criteria), ⇒, , =, , [BPT], , ⇒, , = ⇒, , =, , ⇒ AC : BC = 3:2, , Construction 6.2:, To construct a triangle similar to a given triangle as per given scale factor., Example1:Construct a triangle similar to a given triangle ABC with its sides equal to, of the corresponding side of the triangle ABC [i,e. of scale factor ], Solution: Given a triangle ABC, we are required to construct another triangle whose sides are, of the corresponding sides of the triangle ABC., Step-1: Draw any ray BX making an acute angle, with BC on the side opposite to the vertex A, Step-2: Locate 4 (the greater of 3 and 4 in ), points B1, B2, B3 and B4 on BX so that BB1, = B1 B2 = B2 B3 = B3B4., Step-3: Join B4C and draw a line through B3 the, 3rd point, (3 being smaller of 3 and 4in )parallel, toB4C to intersect BC at C1, Step-3: Dr a w a line t hr oug h C1 pa r a llel, to the line CA to intersect BA at A 1, Justification:, =, , ∴, , =, , =, , ⇒, , =, , C1A1 ǁ CA ∴ ∆ A1BC1 ~ ∆ ABC ⇒, , =, , =, , Example 2 : Construct a triangle similar to a, given triangle ABC with its sides equal to of, the corresponding side of the triangle ABC, [i,e. of scale factor ], Step1: Construct any ∆ABC. Draw any ray BX, making an acute angle with BC on the side, opposite to the vertex A., Step 2: Locate 5 points (the greater of 5 and 3, in ) B1, B2, B3, B4 and B5 on BX such that, BB1= B1B2 = B2B3 = B3B4 = B4B5, Step 3: Join B3( the 3rd point, 3 being smaller of, 3 and 5 in ) to C and draw a through B5 parallel, to B3C intersect BC at C1, P a g e 124 | 159 Available in ykoyyur.blogspot.com, , =

Page 126 :
SSLC Mathematics Solutions – Part -1, , YK, , Step 4: Dr a w a line t hr oug h C1 pa r a llel, to the line CA to intersect BA at A 1 [Note:, Extended BA], Justification:, ∆, ~∆ ′, ⇒, =, =, But,, , =, , ∴, , =, , =, , ⇒, , =, , =, , =, , Exercise 6.1, In each of the following, give the justification of the construction also:, 1. Draw a line segment of length 7.6 cm and divide it in the ratio 5 : 8. Measure the two, parts., , Step-1: Draw any ray AX, making an acute angle with AB, (Can draw above or below the given line), Step-2:Locate 13(5+8) points A1, A2, ---A12, A13, on AX so that AA1 = A1 A2 = A2 A3---A12 A13, Step-3:Join BA13, Step-4: Through the point A5 (m = 5), draw a line parallel to A13 B (by making an angle, equal to AA13 B) at A5 intersecting AB at the point C (see Fig.). Then, AC : CB = 5 : 8, Justification:, A5CǁA13B ⇒, , =, , [BPT] ⇒, , =, , = ⇒ 5:8, , 2. Construct a triangle of sides 4 cm,, 5 cm and 6 cm and then a triangle, similar to it whose sides are of, the corresponding sides of the, first triangle., Step-1: Construct any ∆ABC.Draw, any ray BX making an acute angle, with BC on the side opposite to the, vertex A, Step-2: Locate 3 (the greater of 3, and 4 in ) points B1, B2, B3 on, BX so that BB1 = B1 B2 = B2 B3, Step-3:Join B3C and draw line through B2 (The 2nd point, being smaller of 2 and 3 in ) parallel, to B3C to intersect BC at C1, P a g e 125 | 159 Available in ykoyyur.blogspot.com

Page 127 :
SSLC Mathematics Solutions – Part -1, , YK, , Step – 4: Dr a w a line t hr oug h C1 pa r a llel to the line CA to intersect BA at A 1, Justification:, ∴, , =, 1, , =, , 1, , = ⇒, 1, , =, , 1, , ⇒C A ǁCA, ∴ ∆ A BC ~ ∆ ABC, 3. Construct a triangle with sides 5 cm, 6 cm and 7 cm and then another triangle whose, ssides are of the corresponding sides of first., Step-1: Construct a triangle BC= 7cm,, AB=5cm and AC =6cm, Step-2: Draw any ray BX making an acute, angle with BC on the side opposite to the, vertex A., Step-3: Locate 7 points (the greater of 7 and 5, in ) B1, B2, B3, B4 ---- B7 on BX such that, B1B2 = B2B3 = B3B4 = ---- = B6B7, Step-4: Join B5C( the 5th point, 5 being, smaller of 5 and 7 in, , ) to C and draw a line, , through B7 parallel to B5C intersect BC at C1, [Note:Extended BC], Step-5: Dr a w a line t hr oug h C1 pa r a llel, to the line CA to intersect BA at A1 [Note:, Extended BA], Justification:, ∆, ~∆ ′ ′ ⇒, =, =, But,, ∴, , =, , = ⇒, , =, , =, , =, , =, , 4. Construct an isosceles triangle whose base is 4cm and then another triangle whose sides, are 1, , times the corresponding sides of the isosceles triangle., , Step-1: Construct an Isoceles triangle with base, 8cm and altitude 4cm.,, Step-2: Draw any ray BX making an acute, angle with BC on the side opposite to the, vertex A., Step-3: Locate 3 points (the greater of 3 and 2, in ) B1, B2, B3 on BX such that BB1= B1B2 =, B2B3, Step-4: Join B2( the 5 th point, 5 being smaller, of 5 and 7 in ) to C and draw a line through, B3 parallel to B2C intersect BC at C1, [Note:Extended BC], Step-5: Dr a w a line t hr oug h C1 pa r a llel to the line CA to intersect BA at A 1 [Note:, Extended BA], P a g e 126 | 159 Available in ykoyyur.blogspot.com

Page 128 :
SSLC Mathematics Solutions – Part -1, , YK, , Justification:, ∆, , ~∆ ′, , But,, , =, , ⇒, , =, ∴, , =, , =, = ⇒, , =, , =, , =, , 5. Draw a triangle ABC with side BC = 6cm, AB = 5cm, and ∠ABC = 600 . Then construct, a triangle whose sides are of the corresponding sides of the triangle ABC., Step-1: Construct a ∆ABC with side BC =, 6cm, AB = 5cm and ∠ABC = 600, Step-2: Draw any ray BX making an acute, angle with BC on the side opposite to the, vertex A., Step-3: Locate 4 points (the greater of 4 and 3, in ) B1, B2, B3 , B4 on BX such thatBB1=, B1B2 = B2B3 = B3B4, Step-4: Join B4( the 3 th point, 3 being smaller, of 3 and 4 in ) to C and draw a line through, B3 parallel to B4C intersect BC at C1, Justification:, ∴, , =, 1, , 1, , =, , =, , 1, , ∴ ∆ A BC ~ ∆ ABC, , C A ǁ CA, ⇒, , = ⇒, , =, , 1, , =, , =, , 6. Draw a triangle ABC with side BC = 7cm,, ∠B =45 0 , ∠A =1050 then construct a, triangle whose sides are, , times the, , corresponding sides of ∆ABC., Step-1: Construct a ∆ABC with sideb BC=, 7cm, ∠B =450 , ∠A =1050, Step -2: Draw any ray BX making an acute, angle with BC on the side opposite to the, vertex A., Step-3: Locate 4 points (the greater of 4 and, 3 in ) B1, B2, B3 , B4 on BX such that BB1, = B1B2 = B2B3 = B3B4, Step-4: Join B4( the 4th point, 4 being greater, of 3 and 4 in ) to C and draw a line through, B3 parallel to B4C intersect BC at C1, Step-5: Dr a w a line t hr oug h C1 pa r a llel to the line CA to intersect BA at A1, Justification:, = ∴, 1, , 1, , =, , =, , 1, , ∴ ∆ A BC ~ ∆ ABC, , C A ǁ CA, ⇒, , = ⇒, , =, , 1, , =, , =, , P a g e 127 | 159 Available in ykoyyur.blogspot.com

Page 129 :
SSLC Mathematics Solutions – Part -1, , YK, , 7. Draw a right triangle in which the sides(other than hypotenuse) are lengths 4cm and, 3cm. Then construct another triangle whose sides are times corresponding sides of the, given triangle., Step-1: Construct right with sides 4cm and 3cm, (exept hypotenuse), Step-2: Draw any ray BX making an acute, angle with BC on the side opposite to the, vertex A., Step-3: Locate 4 points (the greater of 3 and 4, in ) B1, B2, B3,B4 on BX such thatBB1= B1B2, = B2B3 = B3B4, Step-4: Join B4( the 4 th point, 4 being greater, of 4 and 3 in ) to C and draw a line through, B3 parallel to B4C intersect BC at C1, Step-4: Dr a w a line t hr oug h C1 pa r a llel, to the line CA to intersect BA at A 1, Justification:, = ∴, C1A1 ǁ CA, ⇒, , =, , = ⇒, , =, , =, , ∴ ∆ A1BC1 ~ ∆ ABC, =, , =, , 6.3 Construction of Tangents to a Circle, To construct the tangents to a circle from a point outside it, We are given a circle with centre O and a point P outside it. We have to construct the two, tangents from P to the circle., Step 1: Join PO and bisect it. Let M be, the mid- point of PO, Step 2: Taking M as centre and MO as, radius, draw a circle. Let it intersect, the given circle at the points Q and R., Step 3: Join PQ and PR, Then PQ and PR are the required, two tangents, Justification:, Join OQ, ∠PQO is an angle in semi, circle, ∴ ∠ PQO = 90 0 ⇒ PQ ⟘OQ, OQ is, the radius of given circle. Therefore, PQ is the tangent to the circle., Similarlly PR also the tangent to the, circle., , P a g e 128 | 159 Available in ykoyyur.blogspot.com

Page 130 :
SSLC Mathematics Solutions – Part -1, , YK, , Exercise 6.2, In each of the following, give also the justification of the construction:, 1. Draw a circle of radius 6 cm. From a point 10 cm away from its centre, construct the pair, of tangents to the circle and measure their lengths., Step-1: Draw PO = 10cm. Join PO and bisect, it. Let M be the mid- point of PO, Step-2: Taking M as centre and MO as radius,, draw a circle. Let it intersect the given circle, at the points Q and R, Step-3: Join PQ and PR measure the length, Then PQ and PR are the required two, tangents, Justfication:, Join O, Q ∠PQO is an angle in semi circle, ∴ ∠ PQO = 90 0 ⇒ PQ ⟘OQ, OQ is the radius, of given circle.Therefore PQ is the tangent to, the circle. Similarlly PR also the tangent to the, circle., ∆ PQO is a right angle triangle, OP2 = OQ2 + PQ2 [ Pythagoras theorem], ⇒ PQ2 = 102 – 6 2, ⇒ PQ2 = 64 ⇒ PQ = 8 cm, 2. Construct a tangent to a circle of radius 4 cm from a point on the concentric circle of, radius 6 cm and measure its length. Also verify the measurement by actual calculation., Step-1: Draw two concentric circles at O with, radius 4cm and 6cm. Locate a point P on, greater circle and join PO. Bisect it. Let M be, the mid- point of PO, Step-2: Taking M as centre and MO as radius,, draw a circle. Let it intersect the given circle, at the points Q, Step-3: Join PQ and mesure the length. It is, ≈4.5cm, Then PQ a≈4.5cm is the required tangent, Justification:, Join O, Q ∠PQO is an angle in semi circle, ∴ ∠ PQO = 90 0 ⇒ PQ ⟘OQ, OQ is the, radius of given circle.Therefore PQ is the, tangent to the circle., ∆ PQO is a right angle triangle, OP2 = OQ2 + PQ2 [ Pythagoras theorem], ⇒ PQ2 = 6 2 – 42, ⇒ PQ2 = 20 ⇒ PQ = 4.47 cm, , P a g e 129 | 159 Available in ykoyyur.blogspot.com

Page 131 :
SSLC Mathematics Solutions – Part -1, , YK, , 3. Draw a circle of radius 3 cm. Take two points P and Q on one of its extended diameter, each at a distance of 7 cm from its centre. Draw tangents to the circle from these two, points P and Q., , Step-1:Construct a circle of radius 3cm at O. Draw a diameter and extend the diameter 7cm, on both sides. Name the end point as p and q. Draw perpendicular bisector of Op and Oq and, they intersect at M and N., Step-2:From centers M and N draw circles of radius MO and NO. These circles intersect the, given circle at A,B and C,D., Step-3: Join p to A and B and q to C and D., Now, pA,pB, qC and qD are the required tangents., Justification:, Join p, A ∠pAO is angle on semi circle., ∴ ∠ pAO = 90 0 ⇒ pA ⟘OA, OA is the radius of the given circle. So, pA has to be a tangent., Similarlly pB, qC, qD are the tangents., , 4., , Draw a pair of tangents to a circle of radius 5 cm which are inclined to each other at an, angle of 60°., Step-1:Construct angle 1200 [180 0- 600], at the center.For this draw a diameter and, construct ∠ROQ = 600. Then we get, ∠ROP = 120 0 at the center., Step-2:Draw two perpendiculars at P and, R and the intersect at A., Now, AP and AR are the required, tangents, Justification:, AR⟘OR [Construction] ⇒∠ARO = 900, And OR is the radius at point of contact., ∴ AR is the tangent. Similarly AP is also, the tangent to the circle., , 5., , Draw a line segment AB of length 8 cm. Taking A as centre, draw a circle of radius 4 cm, and taking B as centre, draw another circle of radius 3 cm. Construct tangents to each, circle from the centre of the other circle., P a g e 130 | 159 Available in ykoyyur.blogspot.com

Page 132 :
SSLC Mathematics Solutions – Part -1, , YK, , Step-1:Draw AB = 8cm. Draw circles of radii 4cm and 3cm at A and B., Step-2:Draw perpendicular bisector to AB, it intersect AB at M, Step-3:Draw a circle with center M and passes through A and B. It intersects a circle of radius, 4cm at P,Q and the circles of radius 3cm at S,R., Step-4:Join BP, BQ,AS and AR. These are required tangents., Justification:, Join AP and BS, ∠APB and ∠ASB are the angles on semi-circles, ∴ ∠APB = 900 and ∠ASB = 90 0, Since, AP and BS are the radius, BP and AS have to be the tangents to the circle., Similarlly BQ and AR are also the tangents., 6. Let ABC be a right triangle in which AB = 6 cm, BC = 8 cm and B = 90°. BD is the, perpendicular from B on AC. The circle through B, C, D is drawn. Construct the tangents, from A to this circle., Step-1:Draw the line segments BC= 8cm.and AB =6cm, perpendicular to each other. Join AC. Thus, ∆ABC is a, right angle triangle., Step-2:Draw perpendicular to BC which meets BC at O, Step-3:With O as center and OB as radius draw a circle, which intersects AC at D then ∠BDC = 90 0 . Thus BD, is perpendicular to AC., Step-4: With a as center and AB as radius draw an arc, cutting the circle at M, Step-5: Join AM. Thus AB and AM are required, tangents., Justification:, In ∆ABC , ∠ABC = 900, ⇒∆ABC is right angle triangle., ⇒AB⟘BO and BO is the radius. So , AB has to be a tangent to the circle., AB = AM [Construction ], ∴ AM is also a tangent., 7. Draw a circle with the help of a bangle. Take a point outside the circle. Construct the pair, of tangents from this point to the circle., P a g e 131 | 159 Available in ykoyyur.blogspot.com

Page 133 :
SSLC Mathematics Solutions – Part -1, , YK, , Step-1:Draw a circle by using a bangle., Step-2: Draw two chords MN and NL, Step-3:Draw perpendicular bisector of, MN and NL they intersect at point O, which is the center of the circle., Step-4: Take a point P outside the, circle join OP and bisect it., Step-5: Let D be the midpoint of OP., Taking D as center and OD as radius,, draw a circle which intersects the given, circle at A and B., Step-6: Join AP and BP. Thus AP and, BP are the required tangents from P, Justification:, Join OA,OB. ∠OAP is the angle lying in the semi-circle., ∴ ∠OAP = 900 ⇒ AP⟘OA,, Since, OA is the radius of the circle with center O. So AP has to be a tangent to the circle., Similarlly BP is also a tangent., , Summary, In this chapter, you have learnt how to do the following constructions:, 1. To divide a line segment in a given ratio, 2. To construct a triangle similar to a given triangle as per a given scale factor, which may be less than 1 or greater than 1., 3. To construct the pair of tangents from an external point to a circle., , P a g e 132 | 159 Available in ykoyyur.blogspot.com

Page 134 :
SSLC Mathematics Solutions – Part -1, , 7, , YK, , Coordinate Geometry, , Coordinate axes:, A set of a pair of perpendicular axes, , |, , and, , |, , Horizontal line, , X - Axis, , X1OX, Vertical line, YOY1, , Y - Axis, , The intersection point of X and Y axes is called the Orgin ′O, , The distance of a point from the y-axis is called its x-coordinate, or abscissa. The distance, of a point from the x-axis is called its y-coordinate, or ordinate. The coordinates of a, point on the x-axis are of the form (x, 0), and of a point on the y-axis are of the form (0, y)., The Coordinate axes divides the plane in to four parts. They are called quadrants., The coordinaes of the orgin is ( , ), , 7.2 Distance Formula, The distance between two points on X-axis or on, the straight line paralle to X-axis is, , Distance =, , −, , The distance between two points on Y-axis or on, the straight line paralle to Y-axis isÀ, , Distance =, , −, , AB = AC + BC, The distance between two points which are, neither on X or Y axis nor on the line paralle to, X orY axis, , =, , (, , −, , ) +(, , −, , ), , The distance between the point P(x,y) and the orgin, , =, , +, , Example 1:Do the points (3, 2), (–2, –3) and (2, 3) form a triangle? If so, name the type, of triangle formed., P(3, 2), Q(−2, −3), R(2, 3), Formula = ( − ) +( − ), P a g e 133 | 159 Available in ykoyyur.blogspot.com

Page 135 :
SSLC Mathematics Solutions – Part -1, PQ =, , YK, , 3 − (−2) + 2 − (−3), , = (3 + 2 ) + (2 + 3 ), = (5) +(5) = √25 + 25 = √50 = 7.07, QR = (−2 − 2) +(−3 − 3), = (−4) +(−6) = √16 + 36 = √52 = 7.21, PR = (3 − 2) +(2 − 3) = (1) +(−1), = √1 + 1 = √2 = 1.41, Since the sum of any two of these distances is, greater than the third distance, therefore the point, P,Q and R form a triangle., Also, PQ2 + PR2 = QR2 by the converse of, Pythagoras theorem ∠P = 90O we have, Therefore, PQR is a right triangle., Example2: Show that the points (1, 7), (4, 2), (–1, –1) and (– 4, 4) are the vertices of a, square., Solution: A (1, 7), B (4, 2), C (-1, -1) and D (-4, 4), AB = (4 − 1) + (2 − 7) = (3) +(−5) = √9 + 25, = √34, (, ), (, ), (, ), (, ), BC = −1 − 4 + −1 − 2 = −5 + −3 = √25 + 9 = √34, CD =, =, =, , −4 − (−1) + 4 − (−1), , (−4 + 1) +(4 + 1), (−3) +(5) = √9 + 25 = √34, , DA =, , 1 − (−4) +(7 − 4), , = (1 + 4) +(3) = (5) +(3) = √25 + 9 = √34, AC = (−1 − 1) +(−1 − 7), = (−2) +(−8) = √4 + 64 = √68, BD = (−4 − 4) +(4 − 2), = (−8) +(2) = √64 + 4 = √68, , Since, AB = BC = CD = DA and AC = BD, all the, four sides of the quadrilateral ABCD are equal and its, diagonals AC and BD are also equal. Thereore, ABCD, is a square, Example 3 : Fig. 7.6 shows the a r r a n gement o f, des ks, in a classroom. Ashima, Bharti and, Camella are seated at A (3, 1), B(6, 4) and C(8, 6), respectively. Do you think they are seated in a line?, G ive r ea s on s for your answer., AB = (6 − 3) +(4 − 1) = (3) +(3), = √9 + 9 = √18 = √9 × 2 = √, BC = (8 − 6) +(6 − 4) = (2) +(2), = √4 + 4 = √8 = √4 × 2 = √, AC = (8 − 3) +(6 − 1) = (5) +(5), = √25 + 25 = √50 = √25 × 2 = √, P a g e 134 | 159 Available in ykoyyur.blogspot.com

Page 136 :
SSLC Mathematics Solutions – Part -1, , YK, , AB + BC = 3√2 + 2√2 = 5√2, Since,, AB + BC = AC we can say that the points A, B and C are collinear., Therefore, they are seated in a line, Example 4 : Find a relation between x and y such that the point (x , y) is equidistant, from the points (7, 1) and (3, 5)., Let the point P (x, y) is equi distance from the, points A (7, 1) and B (3, 5), PA = PB ⇒ PA2 = PB2, PA = (x − 7) +(y − 1), PB = (x − 3) +(y − 5), AP2 = BP2 ⟹, , (x – 7) +(y − 1), , ( x − 3) + ( y − 5), =, (x − 7)2 + (y − 1)2 = (x − 3)2 + (y − 5)2, x + 7 − 2(x)(7) + y + 1 − 2(y)(1) = x + 3 − 2(x)(3) + y + 5 − 2(y)(5), x + 49 − 14x + y + 1 − 2y = x + 9 − 6x + y + 25 − 10y, x − x − 14x + 6x + y − y − 2y + 10y = 34 − 50, −8x + 8y = −16 ÷ −8 ⇒ − = 2, Which is the require relation., Remark :Note that the graph of the equation x – y = 2 is a line. From your earlier studies, you, know that a point which is equidistant from A and B lies on the perpendicular bisector of, AB. Therefore, the graph of x – y = 2 is the perpendicular bisector of AB, Example 5 : Find a point on the y-axis which is equidistant from the points A(6, 5) and, B(– 4, 3)., We know that a point on the y − axis is of the form (0, y). P (0, y) So, let the point P(0, y), be equidistant from A and B. Then PA = PB, (6 − 0)2 + (5 − )2 = (−4 − 0)2 + (3 − )2, 36 + 5 +, − 2(5)( ) = 16 + 3 +, − 2(3)( ), 36 + 25 +, − 10 = 16 + 9 +, −6, −, − 10 + 6 = 25 − 61 ⇒ −4 = −36, =, = 9 Therefore the required point is ( , ), PA = (6 − 0) +(5 − 9) = (6) +(−4) = √36 + 16 = √52, PB = (−4 − 0) +(3 − 9) = (−4) +(−6) = √16 + 36 = √52, , Exercise 7.1, 1. Find the distance between the following pairs of points :, i) (2, 3), (4, 1) ii) (-5, 7), (-1, 3), iii) (a, b), (-a, -b), i) (x , y ) = (2, 3) , (x , y ) = (4, 1), Formula = ( − ) +( − ), d = (4 − 2) +(1 − 3) = (2) +(−2), d = √4 + 4 = √2 × 4 = 2√2 Units, ii) (x , y ) = (−5, 7) , (x , y ) = (−1, 3), d = (−1 − [−5) +(3 − 7) = (4) +(−4), d = √16 + 16 = √2 × 16 = 4√2 Units, iii) (x , y ) = (a, b) ,, , (x , y ) = (−a, −b), , P a g e 135 | 159 Available in ykoyyur.blogspot.com, , 2, , 3, , 4, , 1, , -5, , 7, , -1, , 3

Page 137 :
SSLC Mathematics Solutions – Part -1, (−a − a) +(−b − b ) = (−2a) +(−2b), d = √4a + 4b = 4(a + b ) = 2√a + b Units, , YK, , d=, , a, , b, , -a, , -b, , 2. Find the distance between the points (0, 0) and (36, 15). Can you now find the distance, between the two towns A and B discussed in Section 7.2., (x, y) =(36, 15), d = x +y = √36 +15 = √1296 + 225 = √1521 =, Units, We can find the distance between the two towns A and B.Suppose town A is at the Orgin,, then the town has to be at (36,15). The distance between these two towns is 39km (1, 5),, 3. Determine if the points (1, 5), (2, 3) and (– 2, – 11) are, collinear., A (1, 5), B (2, 3) ªÀÄvÀÄÛ C (-2, -11), AB = (2 − 1) +(3 − 5) = (1) +(−2), = √1 + 4 = √5, BC = (−2 − 2) +(−11 − 3), = (−4) +(−14), = √16 + 196 = √212, AC = (−2 − 1) +(−11 − 5), = (−3) +(−16) = √9 + 256 = √265, AB + BC ≠ AC, ∴ These are non-collinear points, 4. Check whether (5, – 2), (6, 4) and (7, – 2) are, the vertices of an isosceles triangle., Formula d = (x − x ) +(y − y ), PQ =, , (6 − 5) + 4 − (−2), , = (1) +(6) = √1 + 36 = √37, QR = (7 − 6) +(−2 − 4), = (1) +(−6) = √1 + 36 = √37, PR = (7 − 5) +(−2 − [−2]), = (2) +(0) = √4 = 2, (i), (ii), (iii)  PQ = QR,, , ( i), (ii), (iii), , Since,Two sides of the tringle are equal., Hence, ∆PQR is an isosceles triangle., 5. In a classroom, 4 friends are seated at the, points A, B, C and D as shown in Fig. 7.8., Champa and Chameli walk into the class and, after observing for a few minutes Champa asks, Chameli, “Don’t you think ABCD is a, square?” Chameli disagrees. Using distance, formula, find which of them is correct., The coordinates of the points A,B,C and D are,, A(3,4) , B(6, 7) , C(9,4), D(6,1), AB = (6 − 3) +(7 − 4) = (3) +(3), (), = √9 + 8 = √18 = 3√2, BC = (9 − 6) +(4 − 7) =, , (3) +(−3), , P a g e 136 | 159 Available in ykoyyur.blogspot.com

Page 138 :
SSLC Mathematics Solutions – Part -1, ( ), = √9 + 9 = √18 = 3√2, CD = (6 − 9) +(1 − 4) = (−3) +(−3), ( ), = √9 + 9 = √18 = 3√2, DA = (6 − 3) +(1 − 4) = (3) +(−3), ( ), = √9 + 9 = √18 = 3√2, AB = BC = CD = DA, Diagonal AC = (9 − 3) +(4 − 4) = (6) +(0) = √36 = 6, Diagonal BD = (6 − 6]) +(7 − 1) = (0) +(6) = √36 = 6, , YK, , ( ), ( ), , AC = BD, Thus, AB = BC = CD = DA , diagonals: AC = DB, Since all the four sides and diagonals are equal., Hence, ABCD is a square. So, Champa is correct., 6. Name the type of quadrilateral formed, if any, by the following points, and give reasons, for your answer:, i) (-1, -2), (1, 0), (-1, 2), (-3, 0) ii) (-3, 5), (3, 1), (0, 3), (-1, -4) iii) (4, 5), (7, 6), (4, 3), (1, 2), ) (− , − ), ( , ), (− , ),, (− , ), AB =, , 1 − (−1) + 0 − (−2), , = (1 + 1) +(0 + 2) = (2) +(2), = √4 + 4 = √8 = √4 × 2 = 2√2, BC = (−1 − 1) +(2 − 0) = (−2) +(2), = √4 + 4 = √8 = √4 × 2 = 2√2, CD =, =, , −3 − (−1) +(0 − 2) =, , (−3 + 1) +(−2), , (−2) +(−2) = √4 + 4 = √8 = √4 × 2 = 2√2, , DA =, , −3 − (−1) + 0 − (−2), , = (−3 + 1) +(2) = √4 + 4 = √8 = √4 × 2 = 2√2, AB = BC = CD = DA, AC =, , −1 − (−1) + 2 − (−2), , =, , (−1 + 1) +(2 + 2) =, , (0) +(4) = √16 = 4, , BD = (−3 − 1) +(0 − 0) = (−4) +(0) = √16 = 4, Thus, AC = BD, Since, the four sides AB, BC, CD and DA are equal and the diagonals AC = DB are equal., So the quadrilateral ABCD is a square., ii) (-3, 5), (3, 1), (0, 3), (-1, -4), AB =, , 3 − (−3) + 1 − (−3), , = (3 + 3) +(1 + 3) = (6) +(4), = √36 + 16 = √52, BC = (0 − 3) +(3 − 1) = (−3) +(2), = √9 + 4 = √13, CD = (−1 − 0) +(−4 − 3), = (−1) +(−7) = √1 + 49, = √50 = √25 × 2 = 5√2, P a g e 137 | 159 Available in ykoyyur.blogspot.com

Page 139 :
SSLC Mathematics Solutions – Part -1, DA =, , YK, , −3 − (−1) +(−4 − 5), , = (−3 + 1) +(−9) = (−2) +(−9), = √4 + 81 = √85, AB ≠ BC ≠ CD ≠ DA, Since, the four sides AB, BC, CD and DA are not equal.Hence these poist does not form a, quadrilateral., iii) (4, 5), (7, 6), (4, 3), (1, 2), Formula: d = (x − x ) +(y − y ), AB = (7 − 4) +(6 − 5), = (3) +(1) = √9 + 1 = √10, BC = (4 − 7) +(3 − 6), = (−3) +(−3) = √9 + 9, = √18 = √9 × 2 = 3√2, CD = (1 − 4) +(2 − 3), = (−3) +(−1) = √9 + 1 = √10, DA = (1 − 4) +(2 − 5), = (−3) +(−3) = √9 + 9, = √18 = √9 × 2 = 3√2, AB = CD , BC = DA, AC = (4 − 4) +(3 − 5) = (0) +(−2) = √0 + 4 = √4 = 2, BD = (1 − 7) +(2 − 6) = (−6) +(−4) = √36 + 16 = √52 = √4 × 13 = 2√13, AC ≠ DB, Thus opposite sides are equal. AB = CD , & BC = DA, But diagonals are not equal. AC ≠ DB ∴ The given points are forming a parallelogram., 7. Find the point on the x-axis which is equidistant from (2, –5) and (–2, 9)., We know that a point on the X − axis is of the form (x, 0)., Let the point P (x, 0) is equi distance from the points A(2, -5) and B(-2, 9), AP = BP, ( − 2)2 + (0 − (−5))2 = ( − (−2) )2 + (0 − 9)2, ( − 2)2 + 52 = ( + 2 )2 + (−9)2, + 2 − 2( )(2) + 25 =, + 2 + 2( )(2) + 81, −4 + 25 = 4 + 81, −4 − 4 = 81 − 25 ⇒ −8 = 56 ⇒ = = −7, Thus, the required point is (−7, 0), 8. Find the values of y for which the distance between the points P(2, – 3) and Q(10, y) is, 10 units., (x , y ) = (2, −3) ,, , (x , y ) = (10, y),, , d = 10, , Formula: d = (x − x ) +(y − y ), 10 = (10 − 2) +( − (−3)) = (8) +( + 3), 10 = 64 + ( + 3) ⇒ 100 − 64 = ( + 3), ⇒ ( + 3) = 36 ⇒ + 3 = ±√36 ⇒ + 3 = ±6, ⇒ y = 6 − 3 = 3 or x = −6 − 3 = −9, P a g e 138 | 159 Available in ykoyyur.blogspot.com, , 2, , -3, , 10, , y

Page 140 :
SSLC Mathematics Solutions – Part -1, , YK, , 9. If Q(0, 1) is equidistant from P(5, –3) and R(x, 6), find the values of x. Also find the, distances QR and PR., The point Q (0, 1) is equi distance from the points P (5, -3) and R (x, 6), PQ = QR ⇒ PQ2 = PR2, PQ = (5 − 0) +(−3 − 1) = (5 ) +(−4) = √25 + 16 = √41, QR = (x − 0) +(6 − 1) = (x) +(5) = √x + 25, PQ2 = PR2 ⟹ √x + 25 = √41, x + 25 = 41⇒ x = 41 − 25 ⇒ x = 16 ⇒ x = ±√16 ⇒ x = ±4, The coordinate of the point R is (4,6) or (−4,6), If the coordinates of R is (4,6) then,, QR = (4 − 0) +(6 − 1) = (4) +(5) = √16 + 25 = √41, PR = (4 − 5) +(6 − (−3)) = (−1) +(6 + 3) = √1 + 81 = √82, If the coordinates of R is (−4,6) then,, QR = (−4 − 0) +(6 − 1) = (−4) +(5) = √16 + 25 = √41, PR = (−4 − 5) +(6 − (−3)) = (−9) +(6 + 3) = √81 + 81 = √81 × 2 = 9√2, 10. Find a relation between x and y such that the point (x, y) is equidistant from the point, (3, 6) and (– 3, 4)., The point P (x, y) is equidistance from the points A (3, 6) and B (-3, 4)., PA = PB ⇒ PA2 = PB2, PA = (x − 3) +(y − 6), PB = (x − (−3)) +(y − 4), AP2 = BP2 ⟹ (x − 3) +(y − 6), = (x − (−3)) +(y − 4), 2, 2, 2, (x − 3) + (y − 6) = (x + 3) + (y − 4)2, x + 3 − 2(x)(3) + y + 6 − 2(y)(6) = x + 3 + 2(x)(3) + y + 4 − 2(y)(4), x + 9 − 6x + y + 36 − 12y = x + 9 + 6x + y + 16 − 8y, x − x − 6x − 6x + y − y − 12y + 8y = 25 − 45, −12x − 4y = −20 ÷ −4, 3 + − 5 = 0 This is the required relation, 3 + − 5 = 0 is representing a straight line, Thus the point equidistance from the point A and B on the perpendicular bisector of AB, , 7.3 Section Formula, The coordinates of the point P(x, y) which divides the line segment joining points, and ( , ), internally, in the ratio m1 : m2 are, ( , )=, , +, +, , +, +, , ,, , The mid-point of a line segment divides the line segment, in the ratio 1: 1. Then the coordinates of the midpoint, of the line segment,, ( , )=, , +, , ,, , +, , P a g e 139 | 159 Available in ykoyyur.blogspot.com, , ,

Page 141 :
SSLC Mathematics Solutions – Part -1, , YK, , Example 6 : Find the coordinates of the point which divides the line segment joining the, points (4, – 3) and (8, 5) in the ratio 3 : 1 internally., (x , y ) = (4, −3), (x , y ) = (8,5), m : m = 3: 1, ( ) ( ), x=, =, =, = =7, 4, -3, 8, 5, ( ) ( ), y=, =, =, = =3, Therefore the required point is (7,3), Example 7 : In what ratio does the point (– 4, 6) divide the line segment joining the, points A(– 6, 10) and B(3, – 8)?, P(x, y) = (−4, 6), A(x , y ) = (−6, 10) , B(x , y ) = (3, −8), m =? , m =?, (x, y) =, , ,, ( ), , (−4,6) =, −4 =, , (, , Or, , ), , (, , ,, , ), , (, , ), , 6=, , −4m − 4m = 3m − 6 m, −4m − 3m = −6 m + 4m, −7m = −2m, = = ⇒ m : m = 2: 7, We should verify that the ratio satisfies the y-coordinate also., ( ), ( ), =, =, =, =6, Therefore, the point (– 4, 6) divides the line segment joining the points A(– 6, 10) and, B(3, – 8) in the ratio 2 : 7, Example: Find the coordinates of the points of trisection (i.e., points dividing in three equal, parts) of the line segment joining the points A(2, – 2) and B(– 7, 4)., , Let P and Q be the trisection points of AB. ⇒ AP = PQ = QB, Therefore, P divides AB internally in the ratio 1 : 2. Therefore, the coordinates of P, by applying, the section formula,, A(x , y ) = (2, −2) , B(x , y ) = (−7, 4), m = 1, m = 2, m y +m y, m x +m x, P(x, y) = 1 2 2 1 , 1 2 2 1, m1 m2, , =, , (, , =, , ), , ( ), , ,, , ( ), , m1 m2, , (, , ), , =, , ,, , = (−1, 0), , ,, , Now, Q also divides AB internally in the ratio 2 : 1. So, the coordinates of Q are, A(x , y ) = (2, −2) , B(x , y ) = (−7, 4), m = 2, m = 1, m y +m y, m x +m x, Q(x, y) = 1 2 2 1 , 1 2 2 1, m1 m2, , =, , (, , ), , ( ), , ,, , ( ), , m1 m2, , (, , ), , =, , ,, , =, , ,, , = (−4,, , 2), , Therefore, the coordinates of the points of trisection of the line segment joining A and B are, (–1, 0) and (– 4, 2)., P a g e 140 | 159 Available in ykoyyur.blogspot.com

Page 142 :
SSLC Mathematics Solutions – Part -1, , YK, , Example 9 : Find the ratio in which the y-axis divides the line segment joining the, points (5, – 6) and (–1, – 4). Also find the point of intersection., We know that a point on the Y − axis is of the form (0, y). Let the ratio be k : 1, A(x , y ) = (5, −6) , B(x , y ) = (−1, −4), m = k, m = 1, (x, y) =, , ,, (, , (0, y) =, , ), , ⇒0=, y=, , ( ), , (, , ,, , ), , (, , ), , ⇒ −k + 5 = 0 ⇒ k = 5 ⇒ The ratio is 5: 1, , (, , ), , (, , ), , =, , =, , =, , ∴ The coordinates of the point of intersection 0,, Example 10 : If the points A(6, 1), B(8, 2), C(9, 4) and D(p, 3) are the vertices of a, parallelogram, taken in order, find the value of p., Solution: We know that diagonals of a parallelogram bisect each other., So, the coordinates of the mid-point of AC = coordinates of the mid-point of BD, +, +, The coordinates of the Midpoint =, ,, +, , +, , ,, , +, , =, , +, , ,, , ⇒, , =, , +, , 30 = 2p + 16 ⇒ 2p = 30 − 16 ⇒ p =, , ⇒ p=7, , Exercise 7.2, 1. Find the coordinates of the point which divides the join of (–1, 7) and (4, –3) in the, ratio 2 : 3., Let the Coordinates of the Points be(x,y), m : m = 2: 3 (x , y ) = (−1, 7), (x , y ) =, -1, 7, 4, -3, (4, −3) ,, (x, y) =, ,, =, , ( ), , (, , ), , ,, , (, , ), , ( ), , =, , ,, , =, , ,, , ⇒ (x, y)= (1 , 3), , 2. Find the coordinates of the poin ts of trisection of the line segment join ing (4, –1) and, (–2, –3)., Let P and Q are the trisection points of AB, -1, 7, 4, -3, ⇒ AP = PQ = QB, ∴ The point P divides AB internally in the ratio 1 : 2, A(x , y ) = (4, −1) , B(x , y ) = (−2, −3),, m = 1, m = 2, ∴ The coordinates of P is,, P(x, y) =, ,, =, , (, , ), , ( ), , ,, , (, , ), , (, , ), , =, ,, = ,, = 2,, The point Q divides AB internally in the ratio 2 : 1, A(x , y ) = (4, −1) ,, B(x , y ) = (−2, −3) ; m1 = 2, m2 = 1, P a g e 141 | 159 Available in ykoyyur.blogspot.com

Page 143 :
SSLC Mathematics Solutions – Part -1, Q(x, y) =, =, , (, , ), , ,, ( ), , (, , ,, , ), , YK, , [Using section formula], , (, , ), , =, , ,, , =, , ,, , = 0,, , 3. To conduct Sports day activities in your, rectangular shaped school groun ABCD,, lines have been drawn with chalk powder at, a distance of 1m each. 100 flower pots have, been placed at a distance of 1m from each, other along AD, as shown in fig 7.12., Niharika runs th the distance AD on the, 2nd line and posts a green flag. Preet runs, th the distance AD on the eight line and, posts a red flag. What is the distance, between both the flags? If Rashmi has post, a blue flag exactly halfway between the line, segment joining the two flags, where should, she post her flag?, Solution: The distance of green flag, posted by Niharika on the 2 nd line, = × AD = × 100 = 25 m, The distance of red flag posted by Preet on the 8th line, 1, 1, = × AD = × 100 = 20 m, 5, 5, Coordinates of Green flag = (2,25) = (x , y ), Coordinates of red flag = (8,20) = (x , y ), 2, 25, The distance between flags d =, (x − x ) +(y − y ), d = (8 − 2) +(20 − 25) = (6) +(−5) = √36 + 25 = √61 m, The coordinates of blue flag, if Rashmi post in between these two flags be, (x, y) =, ,, =, ,, =, ,, = (5 , 22.5), , 8, , 20, , 4. Find the ratio in which the line segment joining the points (– 3, 10) and (6, – 8) is divided, by (– 1, 6)., P(x, y) = (−1, 6), A(x , y ) = (−3, 10) , B(x , y ) = (6, −8) , m1 =?, m2 =?, (x, y) =, ,, (−1,6) =, −1 =, , ), , (, , ), , ,, , (, , ), , (, , ), , -3, , 10, , 6, , -8, , Or 6 =, , −m − m = 6m − 3 m, −m − 6m = −3 m + m, −7m = −2m, = =, m : m = 2: 7 We should verify that the ratio satisfies the y-coordinate also, ( ), ( ), =, =, =, =6, Therefore, the point (– 1, 6) divides the line segment joining the points A(– 3, 10) and, P a g e 142 | 159 Available in ykoyyur.blogspot.com

Page 144 :
SSLC Mathematics Solutions – Part -1, , YK, , B(6, – 8) in the ratio 2 : 7, 5. Find the ratio in which the line segment joining A(1, – 5) and B(– 4, 5) is divided by thexaxis. Also find the coordinates of the point of division., We know that a point on the X − axis is of the form (x, 0) Let the ratio be k ∶ 1, A(x , y ) = (1, −5) ,, B(x , y ) = (−4, 5), m1 = k, m2 = 1, (x, y) =, ,, (x, 0) =, , (, , ), , ( ), , ( ), , ,, , (, , ), , 0=, 5k − 5 = 0 ⇒5k = 5, k = 1, the ratio is 1: 1, ( ), ( ), x=, =, =, ∴ The coordinates of the point of division =, , −3, 2, , , 0, , 6. If (1, 2), (4, y), (x, 6) and (3, 5) are the vertices of a parallelogram taken in order, find, x and y., Solution:Let A(1,2), B(4,y), C(x,6) and D(3,5) are the vertices of the parallelogram., Since ABCD is a parallelogram, Therefore diagonals AC and BD bisects each other., So, the coordinates of both AC and BD are same., ∴ Mid point of AC = Mid point of BD =, ,, ,, ,, , =, =, , ,, ,, , = ,, =, x+ 1 = 7, 5+ y = 8, x = 7−1, y= 8−5, x = 6, y = 3, 7. Find the coordinates of a point A, where AB is the diameter of a circle whose centre is, (2, – 3) and B is (1, 4)., The center of the Circle is the mid-point of the, diameter, ∴ (x, y) = (2, −3), A(x , y ) =? , B(x , y ) = (1, 4), (x, y) =, ,, (2, −3) =, 1 + x1, , = 2,, , ,, 4 + y1, , = −3, , 1 + x = 4, 4 + y = −6, x = 4 − 1, y = −6 − 4, x = 3, y = −10, , ∴ The coordinates of a point A is (3, −10), 8. If A and B are (-2, -2) and (2, -4) respectively, find the coordinates of P such that AP, = AB and P lies on the line segment AB, Given AP = AB, P a g e 143 | 159 Available in ykoyyur.blogspot.com

Page 145 :
SSLC Mathematics Solutions – Part -1, , YK, , P divides AB in the ratio 3:4, ⇒ AP: PB = 3: 4, Q(x, y) =, ,, =, , ( ), , (, , ), , ,, , (, , ), , (, , ), , -2, =, , ,, , =, , -2, , 2, , -4, , ,, , 9. Find the coordinates of the points which divide the line segment joining A(– 2, 2) and, B(2, 8) into four equal parts, The point X divides AB in the ratio 1: 3, The coordinates of X is,, -2, 2, 2, 8, (x, y) =, ,, =, , ( ), , (, , ), , ,, , ( ), , ( ), , =, , ,, , =, , The point Y is the mid-point of AB, The coordinates of Y, (x, y) =, ,, =, ,, , ,, , =, , = −1,, , ,, , = (0, 5), , The point Z divides AB in the ratio 3: 1, The coordinates of Z is,, (x, y) =, ,, =, , ( ), , (, , ), , ,, , ( ), , ( ), , =, , ,, , =, , ,, , = 1,, , 10. Find the area of a rhombus if its vertices are (3,, 0), (4, 5), (– 1, 4) and (– 2, – 1) taken in, order[Hint: Area of rhombus = (product of its, diagonals)], AC = (−1 − 3) +(4 − 0) = (−4) +(4), = √16 + 16 = √16 × 2 = 4√2, (−2 − 4) +(−1 − 5) =, , BD =, , (−6) +(−6), , = √36 + 36 = √36 × 2 = 6√2, The area of the rhombus = × 4√2 × 6√2, =, , √, , = 12(2) = 24 square units., , 7.4 Area of a Triangle, Area of triangle =, , × base × height, , By Heron’s Formula Area of the triangle = s(s − a)(s − b)(s − c) , Here, s =, a, b and c are the sides of the triangle., We could find the lengths of the three sides of the triangle using distance formula. But this, could be tedious, particularly if the lengths of the sides are irrational number. Then we can, use the following formula to find the area of the triangle., , Area of the triangle = [, , (, , −, , )+, , P a g e 144 | 159 Available in ykoyyur.blogspot.com, , (, , −, , )+, , (, , −, , )]

Page 146 :
SSLC Mathematics Solutions – Part -1, , YK, , Example 11:Find the area of a triangle whose vertices, are (1, –1),(– 4, 6) and (–3, –5)., A (1, -1), B(-4, 6) ªÀÄvÀÄÛ C (-3, -5), Area = [ (, =, , −, , )+, , (, , −, , )+, , (, , −, , )], , 1(6 − (−5)) + (−4) −5 − (−1) + (−3)(−1 − 6), , = [1(6 + 5) + (−4)(−5 + 1) + (−3)(−7)], = [11 + 16 + 21], = (48) = 24, Area of the triangle is = 24 Square units, Example 12 : Find the area of a triangle formed by, the points A(5, 2), B(4, 7) and C (7, – 4)., A (5, 2), B (4, 7) and C (7, -4), Area = [ ( − ) + ( − ) + ( − )], = [5(7 − (−4)) + 4(−4 − 2) + 7(2 − 7)], = [5(7 + 4) + 4(−6) + 7(−5)], = [55 − 24 − 35], = (55 − 59), = (−4) = −2, Since area is a measure, which cannot be negative, we, will take the numerical value of – 2, i.e., 2. Therefore,, the area of the triangle = 2 square units., Example 13 : Find the area of the triangle formed by the points P(–1.5, 3), Q(6, –2), and R(–3, 4)., Area of the triangle= [ ( − ) + ( − ) + ( − )], = [(−1.5)(−2 − 4) + 6(4 − 3) + (−3)(3 − (−2))], = [(−1.5)(−6) + 6(1) + (−3)(3 + 2)], = [9 + 6 − 15] = (15 − 15), = ( 0) = 0, If the area of a triangle is 0 square units, then its vertices, will be collinear., Example 14 : Find the value of k if the points A(2, 3), B(4, k) and C(6, –3) are, collinear., Since the given points are collinear, the area of the triangle formed by them must be 0, i.e.,, [ ( − ) + ( − ) + ( − )] = 0, [2( − (−3)) + 4(−3 − 3) + 6(3 − )] = 0, [2( + 3) + 4(−6) + 6(3 − )] = 0, [2 + 6 − 24 + 18 − 6 ] = 0, (−4 ) = 0 ⇒ k = 0, P a g e 145 | 159 Available in ykoyyur.blogspot.com

Page 147 :
SSLC Mathematics Solutions – Part -1, , YK, , Example 15 : If A(–5, 7), B(– 4, –5), C(–1, –6) and D(4, 5) are the vertices of a, quadrilateral, find the area of the quadrilateral ABCD., By joining B to D, we will get two triangles ABD and BCD, ∴ Area ∆ABD = [x (y − y ) + x (y − y ) + x (y − y )], = [(−5)(−5 − 5) + (−4)(5 − 7) + 4(7 − (−5))], = [(−5)(−10) + (−4)(−2) + 4(7 + 5)] = [50 + 8 + 48], = (106) = 53 Sq.units, 1, ∴ Area ∆BCD = [x (y − y ) + x (y − y ) + x (y − y )], 2, = [(−4)(−6 − 5) + (−1)(5 − (−5)) + 4(−5 − (−6))], = [(−4)(−11) + (−1)(5 + 5) + 4(−5 + 6)], = [44 − 10 + 4] = (38) = 19 Sq.units, Therefore the area of quadrilateral ABCD = 53 + 19 = 72 Sq.units, , Exercise 7.3, 1. Find the area of the triangle whose vertices are :, i) (2, 3), (-1, 0), (2, -4), ii) (-5, -1), (3, -5) (5, 2), i) (2, 3), (-1, 0), (2, -4), Area = [ ( − ) + ( − ) + ( − )], = [2(0 − (−4)) + (−1)(−4 − 3) + 2(3 − 0)], = [2(4) + (−1)(−7) + 2(3)] = [8 + 7 + 6] = (21) =, ii) (-5, -1), (3, -5) (5, 2), Area = [x (y − y ) + x (y − y ) + x (y − y )], , Sq.units, , = [(−5)(−5 − 2) + 3(2 − (−1)) + 5(−1 − (−5))], = [(−5)(−7) + 3(2 + 1) + 5(−1 + 5)] = [35 + 9 + 20] = (64), = 32 Sq.units., 2. In each of the following find the value of ‘k’, for which the points are collinear., i) (7, -2), (5, 1), (3, k) ii) (8, 1), (k, -4) (2, -5), i) (7, -2), (5, 1), (3, k), Since the given points are collinear, the area of the triangle formed by them must be 0, i.e.,, [x (y − y ) + x (y − y ) + x (y − y )] = 0, [7(1 − k) + 5(k − (−2)) + 3(−2 − 1)] = 0, [7(1 − k) + 5(k + 2) + 3(−3)] = 0, [7 − 7k + 5k + 10 − 9] = 0, (−2k + 8) = 0, −2k = −8 ⇒ k =, , =4, , ii) (8, 1), (k, -4) (2, -5), Since the given points are collinear, the area of the triangle formed by them must be 0, i.e.,, [x (y − y ) + x (y − y ) + x (y − y )] = 0, P a g e 146 | 159 Available in ykoyyur.blogspot.com

Page 148 :
SSLC Mathematics Solutions – Part -1, , YK, , [8(−4 − (−5)) + k(−5 − 1) + 2(1 − (−4))] = 0, [8(−4 + 5) + k (−6) + 2(1 + 4)] = 0, [8(1) + k(−6) + 2(5)] = 0, [8 − 6k + 10] = 0, (−6k + 18) = 0, −6k = −18 ⇒ k =, , =3, , 3. Find the area of the triangle formed by joining the mid-points of the sides of the triangle, whose vertices are (0, –1), (2, 1) and (0, 3). Find the ratio of this area to the area of the, given triangle., Let A(0, -1), B(2, 1) and C(0, 3) be the, vertices of the triangle ABC, D, E and F are the mid-point of AB,BC and AC, The coordinates of D, (x, y) =, , ,, , =, ,, = (1, 0), The coordinates of E, y + y, x + x, (x, y) = 2 1 , 2 1 =, 2, , =, , 0+2, , ,, , ,, , 3+ 1, , 4, , =, ,, = (1, 2), The coordinates of F, (x, y) =, ,, , =, , ,, , = 0 ,, = (0, 1), The area of ∆DEF with vertices D(1, 0) , E(1, 2) and F(0, 1), 1, = [ ( − ) + ( − ) + ( − )], 2, = [1(2 − 1) + 1(1 − 0) + 0(0 − 2)] = [1(1) + 1 + 0], = [1 + 1] = (2) = 1 Sq.units, The area of given triangle = [ (, , −, , )+, , (, , −, , )+, , (, , −, , )], , = [0(1 − 3) + 2(3 − (−1)) + 0(−1 − 1)] = [0 + 2(3 + 1)) + 0], = [0 + 8 + 0] = (8) = 4 Sq.units, The ratio of the ∆ABC and ∆DEF = 4: 1, 4. Find the area of the quadrilateral whose vertices, taken in order, are (– 4, – 2), (– 3, – 5),, (3, – 2) and (2, 3)., A(-4, -2), B(-3, -5), C(3, -2) and D(2, 3), By joining B to D, we will get two triangles ABD, and BCD, ∴ Area ABD, , P a g e 147 | 159 Available in ykoyyur.blogspot.com

Page 149 :
SSLC Mathematics Solutions – Part -1, , YK, , 1, = [x (y − y ) + x (y − y ) + x (y − y )], 2, = [(−4)(−5 − 3) + (−3)(3 − (−2)) + 2(−2 − (−5))], , = [(−4)(−8) + (−3)(3 + 2) + 2(−2 + 5)], = [32 − 15 + 6] = (23) =, Sq.units, ∴ AreaBCD, 1, = [x (y − y ) + x (y − y ) + x (y − y )], 2, = [(−3)(−2 − 3) + 3(3 − (−5)) + 2(−5 − (−2))], = [(−3)(−5) + 3(3 + 5) + 2(−5 + 2)], = [15 + 24 − 6] = (33) =, ∴ Area of ABCD =, , +, , =, , Sq.units, = 28 Sq.units, , 5. You have studied in Class IX, (Chapter 9, Example, 3), that a median of a triangle divides it into two, triangles of equal areas. Verify this result for, ABC whose vertices area (4 – 6),, B(3, –2) and, C(5, 2)., Coordinates of D, the midpoint of BC, ( , )=, , +, , =, , =( ,, , ,, , ,, , +, , =, , +, , ,, , −, , ), , Area∆ABD, 1, = [x (y − y ) + x (y − y ) + x (y − y )], 2, = [4(−2 − 0) + 3(0 − (−6)) + 4(−6 − (−2))], = [4(−2) + 3(6) + 4(−6 + 2)], = [−8 + 18 − 16] = (18 − 24), = (−6) = −3 Sq.units, Since area is a measure, which cannot be negative, we will take the numerical value of – 3,, i.e., 3. Therefore, the area of the triangle = 3square units., Area ∆ADC = [x (y − y ) + x (y − y ) + x (y − y )], = [4(0 − 2) + 4(2 − (−6)) + 5(−6 − 0)], = [4(−2) + 4(2 + 6) + 5(−6)] = [−8 + 32 − 30] = (−6) = −3 ZÀz ÀgÀªÀiÁ£ÀUÀ¼ÀÄ, Since area is a measure, which cannot be negative, we will take the numerical value of – 3,, i.e., 3. Therefore, the area of the triangle = 3square units., Hence, the mid-point of a triangle divides it into two triangles of equal areas., , P a g e 148 | 159 Available in ykoyyur.blogspot.com

Page 150 :
SSLC Mathematics Solutions – Part -1, , YK, , 7.5 Summary, 1. The distance between two given points d = (x − x ) +(y − y ), 2. The distance from the orgin to the given points d = x +y, 3. Section formula :P is the point which divides the line segment joining the points, A(x , y ) and B(x , y ), If the point P divides the line in the ratio m: n then the coordinates of P, P(x, y) =, ,, 4. If P is the midpoint of AB, it divides in the ratio 1:1, P £À ¤zÉÃð±ÁAPÀUÀ¼ÀÄ P(x, y) =, ,, 5. Area of triangle = [x (y − y ) + x (y − y ) + x (y − y )], , P a g e 149 | 159 Available in ykoyyur.blogspot.com

Page 151 :
SSLC Mathematics Solutions – Part -1, , YK, , Real Numbers, Euclid’s division algorithm, as the name suggests, has to do with divisibility of integers. Stated, simply, it says any positive integer a can be divided by another positive integer b in such a way, that it leaves a remainder r that is smaller than b., , 8.2 Euclid’s Division Lemma, Theorem 8.1, (Euclid’s Division Lemma) : Given positive integers a and b, there, exist unique integers q and r satisfying a = bq + r, 0 r < b., A lemma is a proven statement used for proving another statement, Example 1 : Use Euclid’s algorithm to find the HCF of 4052 and 12576., 4052, , 12576 3, 12156, 420, , 12576 = 4052 x 3 + 420, 148, , 272 1, 148, 124, , 272 = 148 x 1 + 124, 4, , 24 6, 24, 0, , 420, , 4052 9, 3780, 272, , 4052 = 420 x 9 + 272, 124, , 148 1, 124, 24, , 148 = 124 x 1 + 24, , 24 = 4 x 6 + 0, , 272, , 420 1, 272, 148, , 420 = 272 x 1 + 148, 24, , 124 5, 120, 4, , 124 = 24 x 5 + 4, , ∴ The HCF of 4052 and 12576 is 4, , Example 2 : Show that every positive even integer is of the form 2q, and that every, positive odd integer is of the form 2q + 1, where q is some integer., Solution :Let ‘a’ be a possitive even number,, (i) a = 2q + r here, 0≤ r < 2 ⇒ r must be 0 or 1, But ‘a’ is a positive even number. So r = 0, ∴ a = 2q + 0 ⇒ a = 2q, (ii)Let ‘a’be a positive odd integer , r≠, ⇒r = 1 ∴ a = 2q + 1, Example 3 : Show that any positive odd integer is of the form 4q + 1 or 4q + 3, where q is, some integer., Let a' and b are be a positive integer and a > b, By Division algorithm,, a = bq + r ; 0≤ r < b, If b = 4,, a = (4x2) + r, 0≤ r < 4 ∴ r = 0, 1, 2, 3, i) If r = 0,, a = 4q ⇒a = 2(2q) this is divisible by 2. Therefore this is an even number., ii) If r = 1,, a = 4q + 1 ⇒ a = 2(2q) + 1 this is not divisible by 2. Therefore this is an odd number., P a g e 150 | 159 Available in ykoyyur.blogspot.com

Page 152 :
SSLC Mathematics Solutions – Part -1, , YK, , iii)If r = 2 ,, a = 4q + 2 ⇒ a = 2(2q + 1) This is divisible by 2. Therefore this is an even number., iv) If r = 3 ,, a = 4q + 3 ⇒ a = 2(2q+1) + 1 this is not divisible by 2. Therefore this is an odd number., ∴ Any positive integer is of the form 4q + 1 Or 4q + 3 where q is some integer., Example 4 : A sweetseller has 420 kaju barfis and 130 badam barfis. She wants to, stack them in such a way that each stack has the same number, and they take up the, least area of the tray. What is the number of that can be placed in each stack for this, purpose?, 420 = 130 x 3 + 30, 130 = 30 x 4 + 10, 30 = 10 x 3 + 0, So, the HCF of 420 and 130 is 10., , Therefore the sweetseller can make stacks of 10 for both kinds of burfi, , Exercise 8.1, 1. Use Euclid’s division algorithm to find the HCF of :, (i) 135 and 225 (ii) 196 and 38220 (iii) 867 and 255, (i) 135 ªÀÄvÀÄÛ 225, 135, , 225 1, 135, 90, , 225 = 135 x 1 + 90, ∴ HCF = 45, (ii) 196 ªÀÄvÀÄÛ 38220, 196, , 38220 195, 38220, 0, , 90, , 135 1, 90, 45, 135 = 90 x 1 + 45, , 45, , 90 2, 90, 0, 90 = 45 x 2 + 0, , 38220 = 196 x 195 + 0, ∴ HCF = 196, , (iii) 867 ªÀÄvÀÄÛ 255, 255, , 867 3, 765, 102, , 867 = 255 x 3 + 102, ∴ HCF = 51, , 102, , 255 2, 204, 51, , 255 = 102 x 2 + 51, , 51, , 102 2, 102, 0, , 102 = 51 x 2 + 0, , 2. Show that any positive odd integer is of the form 6q + 1, or 6q + 3, or 6q + 5, where q is, some integer., Let a be a positive integer and let b = 6, Therefore by division algorithm, a = bq + r [ 0 ≤ r < b ], ⇒ a = 6q + r [ r = 0,1,2,3,4,5 ], (i) if r = 0 , a = 6q ⇒ divisible by 2. ∴ 6q is even, (ii) if r = 1 , a = 6q + 1 ⇒ not divisible by 2 ∴ 6q + 1 is odd, (iii) if r = 2 , a = 6q + 2 ⇒ divisible by 2. ∴ 6q + 2 is even, , P a g e 151 | 159 Available in ykoyyur.blogspot.com

Page 154 :
SSLC Mathematics Solutions – Part -1, , YK, , 8.3 The Fundamental Theorem of Arithmetic, Theorem 8.2 (Fundamental Theorem of Arithmetic) : Every composite number can, be expressed ( factorised ) as a product of primes, and this factorisation is unique,, apart from the order in which the prime t h e p r i m e f a c t o r s o c c u r, The Fundamental Theorem of Arithmetic says that every composite number can be, factorised as a product of primes. Actually it says more. It says that given any composite, number it can be factorised as a product of prime numbers in a‘unique’ way, except for, the order in which the primes occur. That is, given any composite number there is one and, only one way to write it as a product of primes, as long as we are not particular about the, order in which the primes occur. So, for example, we regard 2 × 3 × 5 × 7 as the same, as 3 × 5 × 7 × 2, or any other possible order in which these primes are written., Example 5 : Consider the numbers 4n, where n is a natural number. Check whether, there is any value of n for which 4n ends with the digit zero., Solution: If the number 4 n, for any n, were to end with the digit zero, then it would be divisible, by 5. That is, the prime factorisation of 4 n would contain the prime 5. This is not possible, because 4n = (2)2n; so the only prime in the factorisation of 4 n is 2., So, the uniqueness of the Fundamental Theorem of Arithmetic guarantees that there are no, other primes in the factorisation of 4n., So, there is no natural number n for which 4 n ends with the digit zero., Example 6 : Find the LCM and HCF of 6 and 20 by the prime factorisation method., Solution: 6 = 2 1 x 31, 20 = 2 x 2 x 5 = 2 2 x 51, HCF (6,20) = 2 and LCM (6, 20) = 2 x 2 x 3 x 5 = 60, , Any two positive integers a and b, HCF (a, b) × LCM (a, b) = a × b., We can use this result to find the LCM of two positive integers, if we have already found the, HCF of the two positive integers., Example 7 : Find the HCF of 96 and 404 by the prime factorisation method. Hence, find, their LCM., Solution: We can write the prime factors of 96 and 404 are as follows, 96 = 25 x 3 ; 404 = 2 2 x 101, HCF(96,404) = 2 2 = 4, ∴ LCM (96, 404) =, = 9696, Example 8 : Find the HCF and LCM of 6, 72 and 120, using the prime factorisation, method., 6 = 2 x 3 ; 72 = 23 x 3 2; 120 = 23 x 3 x 5, ∴ HCF (6, 72, 120) = 21 x 31 = 2x3 = 6, ∴ LCM (6, 72, 120) = 2 3 x 32 x 5 1 = 8 x 9 x 5 = 360, , P a g e 153 | 159 Available in ykoyyur.blogspot.com

Page 155 :
SSLC Mathematics Solutions – Part -1, , YK, , Exercise 8.2, 1. Express each number as a product of its prime factors:, (i) 140 (ii) 156 (iii) 3825 (iv) 5005 (v) 7429, (i) 140 = 2 × 2 × 5 × 7 = 22 × 5 × 7, (ii) 156 = 2 × 2 × 3 × 13 = 22 × 3 × 13, (iii) 3825 = 3 × 3 × 5 × 5 × 17 = 32 × 52 × 17, (iv) 5005 = 5 × 7 × 11 × 13, (v) 7429 = 17 × 19 × 23, 2. Find the LCM and HCF of the following pairs of integers and verify that LCM × HCF =, product of the two numbers., (i) 26 and 91 (ii) 510 and 92 (iii) 336 and 54., (i) 26 = 2 × 13, 91 =7 × 13, HCF = 13; LCM = 2 × 7 × 13 =182, Product of two numbers = 26 × 91 = 2366, LCM x HCF = 13 × 182 = 2366, ∴ LCM x HCF = Product of two numbers, (ii) 510 = 2 × 3 × 5 × 17, 92 =2 × 2 × 23, HCF = 2; LCM = 2 × 2 × 3 × 5 × 17 × 23 = 23460, Product of two numbers = 510 × 92 = 46920, LCM x HCF = 2 × 23460 = 46920, ∴ LCM x HCF = Product of two numbers, (iii) 336 = 2 × 2 × 2 × 2 × 3 × 7, 54 = 2 × 3 × 3 × 3, HCF = 2 × 3 = 6; LCM = 2 × 2 × 2 × 2 × 3 × 3 × 3 × 7 =3024, Product of two numbers = 336 × 54 =18144, LCM x HCF = 6 × 3024 = 18144, ∴ LCM x HCF = Product of two numbers, 3. Find the LCM and HCF of the following integers by applying the prime factorisation, method (i) 12, 15 and 21 (ii) 17, 23 and 29 (iii) 8, 9 and 25, (i) 12 = 2 × 2 × 3; 15 =3 × 5; 21 =3 × 7, HCF = 3;, LCM = 2 × 2 × 3 × 5 × 7 = 420, (ii) 17 = 1 × 17; 23 = 1 × 23; 29 = 1 × 29, HCF = 1; LCM = 1 × 17 × 19 × 23 = 11339, (iii) 8 =1 × 2 × 2 × 2; 9 =1 × 3 × 3;, 25 =1 × 5 × 5, HCF = 1; LCM = 1 × 2 × 2 × 2 × 3 × 3 × 5 × 5 = 1800, 4. Given that HCF (306, 657) = 9, find LCM (306, 657)., LCM x HCF = Product of two numbers, ×, , ∴ LCM (306, 657) =, = 22338, 5. Check whether 6n can end with the digit 0 for any natural number n., Here, n is a natural number., P a g e 154 | 159 Available in ykoyyur.blogspot.com

Page 156 :
SSLC Mathematics Solutions – Part -1, , YK, , If the number 6n, for any n, were to end with the digit zero, then it would be divisible by 5. That, is, the prime factorisation of 4n would contain the prime 5. This is not possible because the, prime factors of 6 are 2 and 3., Therefore 5 is not a factor of 6. ⇒6n = (2 x 3)n, So, there is no natural number n for which 6 n ends with the digit zero., Explain why 7 × 11 × 13 + 13 and 7 × 6 × 5 × 4 × 3 × 2 × 1 + 5 are composite numbers, , 6. 7 × 11 × 13 + 13 =13 (7x11 + 1) =13(77 + 1 ) =13 (78) =13x2x3x13, The product of two or more than two prime numbers is a composite number., Therefore 7 x 11 x 13 + 13 is a composite number., 7×6×5×4×3×2×1+5, =5(7 × 6 × 4 × 3 × 2 × 1 +1) =5(1008 + 1) =5(1009), The product of two or more than two prime numbers is a composite number., Therefore 7 × 6 × 5 × 4 × 3 × 2 × 1 + 5 is a composite number, 7. There is a circular path around a sports field. Sonia takes 18 minutes to drive one round, of the field, while Ravi takes 12 minutes for the same. Suppose they both start at the, same point and at the same time, and go in the same direction. After how many minutes, will they meet again at the starting point?, To find the time they meet again in the same point, we have to find the LCM of time, 18 = 2 × 3 × 3; 12 = 2 × 2 × 3, LCM = 2 × 2 × 3 × 3 = 36, Therefore after 36 minutes they meet again at the starting point., , 8.4 Revisiting Irrational Numbers, A number which can not be expressed in the form of, , is called irrational number.Here,, , p, q Z, q ≠ 0, Theorem 8.3: Let p be a prime number. If p divides a 2, then p divides a, where a is, a positive integer., Theorm 8.4: √ is irrational., Proof: Let us assume, to the contrary, that √2 is rational., ⇒ √2 = [ p,q∈ Z, q ≠ 0 and (p,q)=1 ], So, there is no other common factors for p and q other than 1, NowÀ, √2 = ⇒ √2q = p Squaring on both sides we get,, (1), √2 = p2 ⇒ 2q2 = p 2, ⇒ 2 divides p2 ⇒ 2, divides p . [ By theorem], ∴ Let p = 2m,, (1) ⇒ 2q 2 = (2m) ⇒q2 = 2m2, ⇒2,divides q 2 ⇒ 2, divides q [By theorem], ∴ 2 is the common factor for both p and q, This contradicts that there is no common factor of p and q ., Therefore our assumption is wrong. So, √2 is a an irrational number., Example 9 : Prove that, , √ is irrational., , Proof: Let us assume, to the contrary, that √3 is rational., P a g e 155 | 159 Available in ykoyyur.blogspot.com

Page 157 :
SSLC Mathematics Solutions – Part -1, ⇒ √3 =, , YK, , [ p,q∈ Z, q ≠ 0 and (p,q)=1 ], , So, there is no other common factors for p and q other than 1, NowÀ, √3 = ⇒ √3q = p Squaring on both sides we get,, (1), √3 = p2 ⇒ 3q2 = p2, 2, ⇒ 3 divides p ⇒ 3 divides p [ By theorem], ∴ Let p = 3m,, (1) ⇒ 3q 2 = (3m) ⇒q 2 = 3m2, ⇒3 divides q 2 ⇒ 3 divides q [ By theorem], ∴ 3 is the common factor for both p and q , This is not possible., Therefore our assumption is wrong. So, √3 is a an irrational number.,  The sum or difference of a rational and an irrational number is irrational and,  The product and quotient of a non-zero rational and irrational number is, irrational., Example 10 : Show that 5 - √ is irrational, Proof: Assume that 5 -√3 is a rational number., ⇒5 - √3 =, ⇒5-, , [ p,q∈ Z, q ≠ 0 and (p,q)=1 ], , = √3, , Here,, , ⇒, , = √3, , is a rational number but √3 is an irrational number. This is not possible, , So, our assumption is wrong. Therefore 5 - √3 is an irrational number., Example 11 : Show that 3√ is irrational., Proof: Assume that 3√2 is a rational number., ⇒3√2 =, , [ p,q∈ Z, q ≠ 0 and (p,q)=1 ], , ⇒ √2 =, Here,, , s a rational number but √2 is an irrational number. This is not possible, , So, our assumption is wrong. Therefore 3√2 is an irrational number DzÀÝjAzÀ 3√2 MAzÀÄ, , Exercise 8.3, 1. Prove that √ is irrational., Proof: Let us assume, to the contrary, that √5 is rational., ⇒ √5 = [ p,q∈ Z, q ≠ 0 and (p,q)=1 ], So, there is no other common factors for p and q other than 1, NowÀ, √5 = ⇒ √5q = p , squaring on both sides we get,, (1), √5 = p2 ⇒ 5q2 = p2, 2, ⇒ 5 divides p ⇒ 5 divide s p [ By theorem], ∴ Let p = 5m,, (1) ⇒ 5q 2 = (3m) ⇒q 2 = 5m2, ⇒5 divides q 2 ⇒ 5 divides q [ By theorem], ∴ 5 is the common factor for both p and q ; this is not possible, Therefore our assumption is wrong. So, √5 is a an irrational number., P a g e 156 | 159 Available in ykoyyur.blogspot.com

Page 158 :
SSLC Mathematics Solutions – Part -1, , YK, , 2. Prove that 3 + 2√ is irrational., Proof: Assume that 3 +2√5 is a rational number., ⇒3 + 2√5 =, ⇒2√5 =, , [ p,q∈ Z, q ≠ 0 and (p,q)=1 ], , - 3 ⇒ √5 =, is a rational number but √5 is an irrational number. This is not possible, , Here,, , So, our assumption is wrong. Therefore 3 + 2√5 is an irrational number., 1. Prove that the following are irrationals:, (i ), (ii) 7√5 (iii) 6 + √2, √, , (i), , √, , Proof: Assume that, ⇒, ⇒, , √, √, , √, , is a rational number., , = [ p,q∈ Z, q ≠ 0 and (p,q)=1 ], =, , Here,, , ⇒ √2 =, is a rational number, but √2 is an irrational. This is impossible., , Therefore our assumption is wrong., , ∴, , √, , is an irrational number., , (ii) 7√, Proof: Assume that 7√5 is a rational number., 7√5 = [ p,q∈ Z, q ≠ 0 and (p,q)=1 ], ⇒√5 =, Here,, , is a rational number, but √5 is an irrational. This is impossible., , Therefore our assumption is wrong. ∴ 7√5 is an irrational number., (iii) 6 + √, Proof: Assume that 6 + √2 is a rational number, ⇒6 + √2 = [ p,q∈ Z, q ≠ 0 and (p,q)=1 ], ⇒ √2 =, Here,, , – 6, , ⇒√2 =, , is a rational number, but √2 is an irrational. This is impossible., , Therefore our assumption is wrong. ∴ 6 + √2 is an irrational number., , 8.5 Revisiting Rational Numbers and Their Decimal Expansion:, Theorem 8.5: Let x be a rational number whose decimal expansion, terminates.Then x can be expressed in the form, where p and q are, coprime, and the prime factorisation of q is of the form 2 n.5 m, where n, m are, non-negative integers., Theorem 8.6 : Let x = be a rational number, such that the prime, factorisation of q is of the form 2n5m, where n, m are non-negative integers., Then x has a decimal expansion which terminates., , P a g e 157 | 159 Available in ykoyyur.blogspot.com

Page 159 :
SSLC Mathematics Solutions – Part -1, , YK, , Theorem 8.7 : Let x = be a rational number, such that the prime factorisation of q, is not of the form 2n5m, where n, m are non-negative integers. Then, x has a decimal, expansion which is non-terminating repeating (recurring)., , Exercise 8.4, 1., , Without actually performing the long division, state whether the following rational, numbers will have a terminating decimal expansion or a non-terminating repeating decimal, expansion, (i), (ii), (iii), (iv), (v), (vi), (i), , (vii), , (viii), , (ix), , (x), , - Factorising the denominator 3125 =5 × 5 × 5 × 5 × 5 = 20 x 5 5, , Here, The factors of 3125 is of the form 2n.5m. So,, (ii), , - Factorising the denominator 8 =2 × 2 × 2 = 23x50, , Here, The factors of 8 is of the form 2n.5m . So,, (iii), , has a terminating decimal expansion., has a terminating decimal expansion., , - Factorising the denominator 455 =5 × 7 × 13, , Here, The factors of 455 is 5x7x13 is not in the form 2n x 5 m, So, this has non-terminating repeating decimal expansion., (iv), , - Factorising the denominator 1600 =2 × 2 × 2 ×2 × 2 × 2 × 5 × 5 = 26 × 52, , Here, The factors of 1600 is of the form 2n.5m., So,, (v), , has a terminating decimal expansion., - Factorising the denominator 343 = 7 × 7 × 7 = 73, , Here, The factors of 343 is not in the form 2 n × 5m, So, this has non-terminating repeating decimal expansion., - denominator is of the form 2n x 5 m, , (vi), So,, , has a terminating decimal expansion., denominator is not in the form 2n x 5 m, , (vii), , So, this has non-terminating repeating decimal expansion., (viii), ⇒ = dinominator 20 x 5 1 is of the form 2 n x 5m, So,, , has a terminating decimal expansion., , (ix), , ⇒, , So,, , has a terminating decimal expansion., , x), , =, , ⇒, , dinominator 21 x 51 is of the form 2n x 5 m, , =, , =, , dinominator not in the form 2 n x 5m, , =, , So, this has non-terminating repeating decimal expansion., 2. Write down the decimal expansions of those rational numbers in Question 1 above, which have terminating decimal expansions., (i), , ⇒, , x, , =, , (ii), , ⇒, , =, , x, , =, =, , = 0.00416, = 2.125, , P a g e 158 | 159 Available in ykoyyur.blogspot.com

Page 160 :
SSLC Mathematics Solutions – Part -1, (iii), , =, , ⇒, , (iv), (v), , =, , ⇒, , =, , = 0.009375, , =, =, , x =, , YK, , = 0.115, , = 0.4, , (vi), ⇒, = = 0.7, 3. The following real numbers have decimal expansions as given below. In each case,, decide whether they are rational or not. If they are rational, and of the form, what can, you say about the prime factors of q?, (i), ., (ii) 0.120120012000120000... (iii) ., (i) 43.123456789 - has a terminating decimal expansion., Therefore this in a rational number and is of the form, and q is of the form 2 nx5 m ⇒, , =, , (ii) 0.120120012000120000..., this has non-terminating and non- repeating decimal expansion., Therefore this is an irrational number, (iii) 43. 123456789 - this has non-terminating repeating decimal expansion., Therefore this in a rational number and is of the form, Let, , = 43. 123456789, , (1), , ⇒ 1000000000x = 43123456789123456789….., (2), (1) – (2) = 999999999x = 43123456746, x=, this is of the form . i.e., the factors of 999999999 is not in the form 2 n x 5 m, , Summery:,  Euclid’s Division Lemma: Given positive integers a and b, there exist whole numbers q, , , , , , , , , and r satisfying a = bq + r, 0 ≤ r < b, Euclid’s division algorithm: This is based on Euclid’s division lemma. According to this,, the HCF of any two positive integers a and b, with a > b, is obtained as follows:, Step 1 : Apply the division lemma to find q and r where a = bq + r, 0 ≤ r < b, Step 2 : If r = 0, the HCF is b. If r ≠ 0 apply Euclid’s lemma to b and r., Step 3 : Continue the process till the remainder is zero. The divisor at this stage will be, HCF (a, b). Also, HCF(a, b) = HCF(b, r)., The Fundamental Theorem of Arithmetic :, Every composite number can be expressed (factorised) as a product of primes, and this, factorisation is unique, apart from the order in which the prime factors occur., If p is a prime and p divides a2, then p divides a, where a is a positive integer., Let x = be a rational number, such that the prime factorisation of q is of the form 2n5 m,, , where n, m are non-negative integers. Then x has a decimal expansion which terminates.,  Let x = be a rational number, such that the prime factorisation of q is not of the form 2n5 m,, where n, m are non-negative integers. Then, x has a decimal expansion which is nonterminating repeating (recurring)., , P a g e 159 | 159 Available in ykoyyur.blogspot.com