Page 1 :
TARGET, classes, anytime, as frequentiy as you like, till it becomes a habit!, Presenting woras and, concePts as Pictures!!, When?, To unlock the imagination, and come up with ideas, To remember facts and, What?, MIND MAP, An INTERACTIVE MAGICAL TOOL Why?, figures easily, TO make clearer and, better notes, Result, TO concentrate and save, How?, time, TO plan with ease and ace, exams, Learning made SiMPle, 'a winning combination', With a blank sheet of paper, COloured Pens and, Your creative imagination!, mind maps for each chapter show the breakthrough system of planning and note-taking, which help make schoolwork fun and cut homework time in half !

Page 2 :
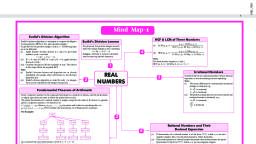
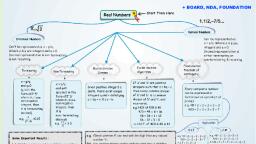
2], CHAPTER : 1 REAL NUMBERS, mInD MAPS, Division Lemma, Given positive integers a, and b, there exist unique integers, q and r satisfying, a = bq +r; 0<r<b, LEARNING maDE SIMPLE, 1. Let p be a prime number., If p divides a², then p divides a,, where a is a positive integer, 2. 2N3 are irrational, Euclid's, Theorems, Division Algorithm, 3. Let x be a rational number whose, Steps to obtain the HCF of two, positive integers, say c and d,, with c>d, decimal expansion terminates. Then x can be, expressed in the form, where p & q are, coprime, the prime factorisation of q is of, the form 2" 5 where n, m are non-, negative integers, Step 1: Apply Euclid's Division, Lemma, to c & d. c = dq + r, Real Numbers, 4. Let x =, a be a rational number such, Step 2: If r= zero, d is the, HCF of c and d If r 0, apply Euclid', that the prime factorisation of q is of the, form 2" 5m where n, m are non-negative, integers. Then, x has a decimal expansion, which terminates., Division to d and r, Fundamental Theorem of Arithmetic, Step 3: Continue the process, till the remainder is zero, Prime Factorization Method, 5. Let x =, 7 be a rational number, such, that the prime factorisation of q is not of, the form of 2"5m where n, m are non-negative, integers. Then, x has a decimal expansion, which is non-terminating repeating, Every composite number, can be expressed as a product of, primes, and this factorisation is unique,, apart from the order in which the, prime factors occur, Composite Number, x = P1×P2× P3...xP,, where P1P2 ... P, are, prime numbers, For any two positive integers,, a and b, HCF (a, b) x LCM (a, b) =a x b, For Example, Ax) = 3x2y, g(x) = 6xy2, HCF = 3xy, LCM = 6x?y?

Page 3 :
[ 3, all, CHAPTER : 2 POLYNOMIALS, If p(x) and g(x) are, two polynomials with, MIND MAPS, Parabola, - əy 0 + (x)8, (x)4 + (x)b x (x)8 =(x)d, LEARNING maDE SIMPLE, Quadratic, a and B are, zeroes of Quadratic, Polynomial, where, r(x) = 0 or, degree of r(x) < degree, (x)8 30, 3+ x9 + *D, Then, Sum of zeroes,, Graphical Representation, Quadratic Polynomial, (0 ), Division Algorithm, -= g +0, Product of zeroes:, 4(0, -4), 5 = go, (9-7), Relationship-Zeroes and, Coefficient of Polynomials,, (9- 1), Cubic, y = x-3x-4, a, B and y are zeroes, of Cubic Polynomial, Polynomials, Sum of zeroes,, p + x) + *9 + xD, ワ-=A + +0, Highest power of, x in Polynomial, p(x), Sum of products of the, :zeroes taken two at a time:, Degree of Polynomial, Zeroes of Polynomial, Graphically, aß + By + ya =, Product of zeroes, = Ago, sədkL, Polynomial Degree General Form, Casel- Graph cuts, x-axis at 2 points, Case2- Graph cuts, x-axis at exactly one point, Case3- Graph, does not cut r-axis, Linear, ax+bx+c, Quadratic, 0まり, Cubic, Number of Zeroes 2, Number of Zeroes 1, Number of Zeroes 0

Page 4 :
4 ], CHAPTER : 3 PAIR OF LINEAR EQUATIONS IN TWO VARIABLES, mInD MAPS, By Substitution, Solve: 7x-15y = 2 -(i), x+2y = 3 -(ii), LEARNING madE SIMPLE, 0 = b+n9+xo, azx+bzy+g = 0, a1,b1,9,a2, b2,2, – Real numbers, Solution: From equation (ii), x = 3-2y, substitute value of x in eq. (i), 7(3-2y)-15y = 2, 61, -29y = -19 y=, 67, Now, from x = 3 – 2y, General Form, Each solution (x, y), corresponds, to a point on the line representing, the equation and vice-versa, Algebraic Methods, 61, (67, x = 3 - 2, 67, Solution Graphically, By Elimination, Solve: x+3y = 6, 2x+3y = 12, Now, Adding equation (i) and (ii), 3x = 18 or x = 6, Pair of Linear Equations, in Two Variables, (!) –, Graphical Representation, Pair of Lines =x-2y = 0, 3x+4y-20 = 0, Again, from (i) x2- (ii), 3y = 0 or, y =0, Hence, x = 6, y = 0, b 7- 1g I, 07-, P(0, 5), 3' b2, %3D, a2, Compare the Ratios = -, dx+4y 20, a2 bz, lg Ip, By Cross-Multiplication, A(0, 0), B(2, 1), Solve: 2x+3y-46 = 0 -(i), 3x+5y-74 = 0 -(ii), Algebraic Interpretation : Exactly, one solution - consistent (unique), Graphical Representation, Intersecting Lines, Solution: By cross-multiplication method, Graphical Representation, Pair of Lines = 2x+3y-9 = 0, 4x+6y-18 = 0, Graphical Representation, Pair of Lines = x+2y-4 = 0, 2x+4y-12 = 0, -74, £., 3, E-, -18, Then,, (0, 3), 3(-74)-5(-46), (-46)(3)-(-74)(2), -P(0, 3), a2, 4' b2, %3D, a2 2' b2, %3D, 4' c2, -12, 2(5)-3(3), Ip, Compare the Ratios = =, R(0, 2) -, Compare the Ratios =, (I'E), (o's't), (o '9)0, ig zp, Algebraic Interpretation = Infinitely, many solutions - Dependent, キ, -138+148, OEZ+ZZz-, ią ip, 6-01, Algebraic Interpretation : No solution, Inconsistent, S(4, 0), Y Coincident Lines, OL 8, i.e.x 8 and y = 10, Parallel Lines

Page 5 :
[ 5, CHAPTER : 4 QUADRATIC EQUATIONS, mInD MAPS, By Completing the Square, Solve: 2x-5x+3 0, Solution: 2x2-5x+3 = 0, LEARNING madE SIMPLE, x+, +, Equation of degree 2,, in one variable, %3D, 4., Meaning, 5, 3, I =x 10, General Form, ax2+bx+c = 0, a, b, c- real numbers, Quadratic, Solution of a, Quadratic Equation, Equations, Quadratic Formula, By Factorization, Find roots of 6x2-x-23D0, Nature of Roots, Roots of ax2+bx+c = 0 are given by, Solution: 6x2+3x-4x-2 0, 3x(2x+1)-2(2x+1) = 0, (3x-2)(2x+1)% 3D0, 0 <a'I, Two distinct real root., For quadratic equation, ax2+bx+c = 0,, 62 4ac is Discriminant (D), The roots of 6x-x-2=0, (3x-2) = 0 or (2xr+1) = 0:, 0 = a'7, Two equal real roots, -1, = X 10, I- 7, 3' 2, Roots are, 0 > a'E, No real roots (imaginary).