Page 1 :
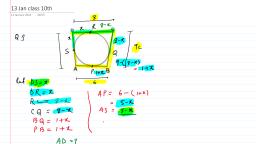
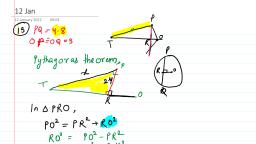
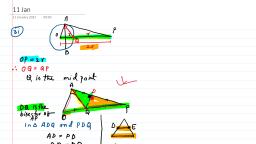
Tia, , 90, , Dz., , 1., , 0K/s ¥ © W “ul G24 1, , Foundation Science: Physics for Class 9, , Long-Answer Questions, , Answer the following in not more than 70 words., If each object in the universe attracts every other, object, why don’t two books kept on a table come, towards each other and collide?, , - State Newton's law of gravitation and write the, , mathematical equation describing it., , . What are the differences between G and g? Are both, , of them universal constants?, , | Show from Newton’s law of gravitation and, , Newton’s second law of motion that the acceleration, of a freely falling body does not depend on the mass, of the body., , . What is the relation between the mass m and the, , weight W of a body? What are the differences, between the two?, , . The acceleration due to gravity for falling bodies is, , taken to be constant. Justify this in view of the fact, that the distance of a falling body from the earth’s, surface keeps changing., , . Show that if a body is taken to a height H above the, , earth’s surface, acceleration due to gravity is, decreased by the factor R?/(R + H)?, where R is the, radius of the earth., , . Show that the acceleration due to gravity at the, , surface of the moon is about one-sixth of that at the, surface of the earth., , E. Numerical Problems, , 1., , Calculate the gravitational force between a 10-kg, ball and a 20-kg ball placed at a separation of 5 m., , . Three balls A, B and C are kept ina straight line. The, , separation between A and C is 1 m, and B is placed, at the midpoint between them. The masses of A, B,C, are 100 g, 200 g and 300 g respectively. Find the net, gravitational force on (a) A, (b) B, and (c) C., , . A particle of mass m, is kept at x = 0 and another of, , mass m, at x = d. When a third particle is kept at, x = d/4, it experiences no net gravitational force due, to the two particles. Find m, /m,., , . The acceleration due to gravity near the earth’s, , surface is 9.8 m/s*, and the earth’s radius is, 6A00 km. From this data calculate the mass of the, earth. Use any universal constant if required., , . Two particles of mass 200 g each are placed at a, , Separation of 10 cm. Assume that the only forces, acting on them are due to their gravitational, attraction. Find the acceleration of each when they, are allowed to move., , . A particle weighs 120 N on the surface of the earth,, , At what height above the earth’s surface will its, weight be 30 N? Radius of the earth = 6,400 km., , . Suppose the earth shrinks such that its radius, , decreases to half the present value, What will be the, acceleration due to gravity on the surface of the, earth?, , 8., , 9., , 10., , 11., , A body weighs 120 N on the earth. Find its, approximate weight on the moon., , Calculate the value of the acceleration due to gravity, at a place 3,200 km above the surface of the earth., , The acceleration due to gravity at a place is 0.2 m/s’., Find its height above the earth’s surface., , As one moves to a place 3,200 km above the earth’s, surface, the acceleration due to gravity reduces to, 4/9 of its value at the earth’s surface. Calculate the, radius of the earth from this data., , . A ball is dropped from a cliff. Find (a) its speed 2s, , after it is dropped, (b) its speed when it has fallen, through 78.4 m, and (c) the time taken in falling, through 78.4 m., , . A ball is thrown upwards with a speed of 39.2 m/s., , Calculate (a) the maximum height it reaches, and, (b) the time taken in reaching the maximum height., , . A ball thrown upwards takes 4 s to reach the, , maximum height. Find (a) the initial speed with, which it was thrown, and (b) the maximum height, reached., , . An object thrown upwards reaches the highest point, , in 5.0 s. Find the velocity with which it was thrown., , . A stone thrown upwards attains a maximum height, , of 19.6 m. Find the velocity with which it was, thrown., , . A body is thrown upwards with a velocity of, , 20 m/s. How much time will it take to return to its, original position?, , . A ball is dropped from a height 2.50 m above the, , floor. (a) Find the speed v with which it teaches the, floor. (b) The ball now rebounds. The speed of the, , ball is decreased to 3v / 4 due to this collision. How, high will the ball rise?, , . A stone is dropped from a cliff at 2:30:30 Pp-m. (hour:, , minute:second). Another stone is dropped from the, same point at 2:30:31 p.m. Find the separation, between the stones at (a) 2:30:31 P-m., (b) 2:30:35, p.m., , . A ball is thrown upwards from the surface of the, , moon with a velocity of 19.6 m/s, (a) How much, time will it take to attain the maximum height? (b), How high will it go?, , . A flowerpot drops from the edge of the roof of a, , multistoried building. Calculate the time taken by, the pot to cross a particular distance AB of height, 2.9 m, the upper point A being 19.6 m below the roof., , . A wicketkeeping glove is dropped from a height of, , 40 m and simultaneously a ball is thrown upwards, , from the ground with a speed of 40 m/s. When and, where do they meet?, , . A boy ona 78.4-m-high cliff drops a stone. One, , second later, he throws another stone downwards, with some speed. The two stones reach the ground, , simultaneously. Find the speed with which the, second stone was thrown,