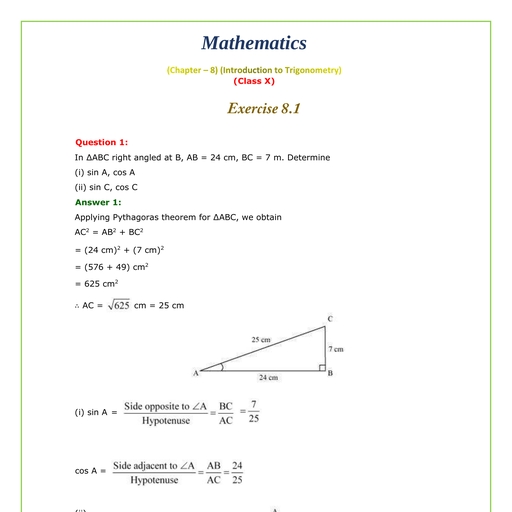
Page 1 :
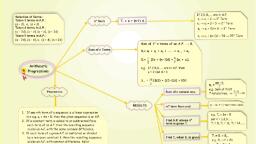
tt ©, o N, be C, re ER, pu T, bl, is, he, d, CHAPTER 5, , ARITHMETIC PROGRESSIONS, , (A) Main Concepts and Results, , •, , An arithmetic progression (AP) is a list of numbers in which each term is, obtained by adding a fixed number d to the preceding term, except the first term, a. The fixed number d is called its common difference., The general form of an AP is a, a + d, a + 2d, a + 3d,..., , •, , In the list of numbers a 1, a 2, a3 ,... if the differences a 2 – a 1, a 3 – a 2, a 4 – a 3,..., give the same value, i.e., if ak + 1 – a k is the same for different values of k, then, the given list of numbers is an AP., , •, , The n th term an (or the general term) of an AP is an = a + (n – 1) d, where a is, the first term and d is the common difference. Note that a1 a., , •, , The sum Sn of the first n terms of an AP is given by, Sn =, , n, [2a + (n – 1) d], 2, , no, , If l is the last term of an AP of n terms, then the sum of all the terms can also be, given by, Sn =, , n, [a + l], 2, , Sometimes Sn is also denoted by S.

Page 2 :
ARITHMETIC PROGRESSIONS, , •, , 45, , If Sn is the sum of the first n terms of an AP, then its nth term an is given by, a n = Sn – Sn – 1, , (B) Multiple Choice Questions, , tt ©, o N, be C, re ER, pu T, bl, is, he, d, , Choose the correct answer from the given four options:, , Sample Question 1 : The 10th term of the AP: 5, 8, 11, 14, ... is, (A), , 32, , (B) 35, , (C) 38, , (D) 185, , Solution : Answer (A), , Sample Question 2 : In an AP if a = –7.2, d = 3.6, an = 7.2, then n is, (A), , 1, , (B) 3, , (C) 4, , (D) 5, , Solution : Answer (D), , EXERCISE 5.1, , Choose the correct answer from the given four options:, 1., , In an AP, if d = –4, n = 7, an = 4, then a is, (A) 6, , 2., , (B) 3.5, , (A), , an AP with d = – 16, , (B), , an AP with d =, , (C), , an AP with d = – 4, , (D), , not an AP, , (C) 103.5, , (D) 104.5, , 4, , The 11 th term of the AP: –5,, , (A) –20, , 5., , (D) 28, , The list of numbers – 10, – 6, – 2, 2,... is, , no, , 4., , (C) 20, , In an AP, if a = 3.5, d = 0, n = 101, then a n will be, (A) 0, , 3., , (B) 7, , (B) 20, , –5, 5, , 0, , ...is, 2, 2, (C) –30, , (D) 30, , The first four terms of an AP, whose first term is –2 and the common difference, is –2, are

Page 3 :
46, , EXEMPLAR PROBLEMS, , – 2, 0, 2, 4, , (B), , – 2, 4, – 8, 16, , (C), , – 2, – 4, – 6, – 8, , (D), , – 2, – 4, – 8, –16, , tt ©, o N, be C, re ER, pu T, bl, is, he, d, , (A), , 6., , The 21st term of the AP whose first two terms are –3 and 4 is, , (A) 17, , 7., , (D) –143, , (B) 33, , (C) 37, , (D) 38, , Which term of the AP: 21, 42, 63, 84,... is 210?, (A) 9th, , 9., , (C) 143, , If the 2nd term of an AP is 13 and the 5 th term is 25, what is its 7th term?, (A) 30, , 8., , (B) 137, , (B) 10th, , (C) 11 th, , (D) 12th, , If the common difference of an AP is 5, then what is a18 – a13 ?, (A) 5, , (B) 20, , (C) 25, , (D) 30, , 10. What is the common difference of an AP in which a 18 – a 14 = 32?, (A) 8, , (B) – 8, , (C) – 4, , (D) 4, , 11. Two APs have the same common difference. The first term of one of these is, –1 and that of the other is – 8. Then the difference between their 4th terms is, (A) –1, , (B) – 8, , (C) 7, , (D) –9, , 12. If 7 times the 7th term of an AP is equal to 11 times its 11 th term, then its 18th, term will be, (A) 7, , (B) 11, , (C) 18, , (D) 0, , 13. The 4th term from the end of the AP: –11, –8, –5, ..., 49 is, (A) 37, , (B) 40, , (C) 43, , (D) 58, , 14. The famous mathematician associated with finding the sum of the first 100 natural numbers is, (B), , Newton, , (C) Gauss, , (D), , Euclid, , no, , (A) Pythagoras, , 15. If the first term of an AP is –5 and the common difference is 2, then the sum of, the first 6 terms is, (A) 0, , (B) 5, , (C) 6, , (D) 15

Page 4 :
ARITHMETIC PROGRESSIONS, , 47, , 16. The sum of first 16 terms of the AP: 10, 6, 2,... is, (A) –320, , (B) 320, , (C) –352, , (D) –400, , 17. In an AP if a = 1, a n = 20 and Sn = 399, then n is, (B) 21, , (C) 38, , (D) 42, , tt ©, o N, be C, re ER, pu T, bl, is, he, d, , (A) 19, , 18. The sum of first five multiples of 3 is, (A) 45, , (B) 55, , (C) 65, , (D) 75, , (C) Short Answer Questions with Reasoning, , Sample Question 1: In the AP: 10, 5, 0, –5, ... the common difference d is equal to 5., , Justify whether the above statement is true or false., Solution :, , a 2 – a1 = 5 – 10 = – 5, a 3 – a2 = 0 – 5 = – 5, , a 4 – a3 = –5 – 0 = – 5, , Although the given list of numbers forms an AP, it is with d = –5 and not with d = 5, , So, the given statement is false., , Sample Question 2 : Divya deposited Rs 1000 at compound interest at the rate of, 10% per annum. The amounts at the end of first year, second year, third year, ..., form, an AP. Justify your answer., Solution :, , Amount at the end of the 1st year = Rs 1100, , Amount at the end of the 2nd year = Rs 1210, , Amount at the end of 3rd year = Rs 1331 and so on., , So, the amount (in Rs) at the end of 1st year, 2nd year, 3rd year, ... are, , no, , 1100, 1210, 1331, ..., , Here,, , a 2 – a1 = 110, , a 3 – a 2 = 121, , As,, , a 2 – a1 ≠ a 3 – a 2, it does not form an AP.

Page 5 :
48, , EXEMPLAR PROBLEMS, , Sample Question 3: The nth term of an AP cannot be n2 + 1. Justify your answer., Solution :, Here, an n 2 1, a1 12 1 2, , tt ©, o N, be C, re ER, pu T, bl, is, he, d, , So,, , a2 2 2 1 5, , a3 3 2 1 10, , #, List of numbers becomes 2, 5, 10, ..., , Here, 5 – 2, , 10–5, so it does not form an AP., , Alternative Solution 1:, , We know that in an AP, d an – an –1, Here, an n 2 1, So,, , an – a n –1, , ( n 2 1) – ( n –1) 2 1, , = 2n – 1, , As an – a n –1 depends upon n, d is not a fixed number., , So, an n 2 1 cannot be the n th term of an AP., Alternative Solution 2:, We know that in an AP, , no, , an =a + ( n –1) d . We observe that an is a linear polynomial in n., , Here, an n 2 1 is not a linear polynomial in n. So, it cannot be the nth term of an AP.

Page 6 :
ARITHMETIC PROGRESSIONS, , 49, , EXERCISE 5.2, 1. Which of the following form an AP? Justify your answer., (i) –1, –1, –1, –1, ..., , tt ©, o N, be C, re ER, pu T, bl, is, he, d, , (ii) 0, 2, 0, 2, ..., (iii) 1, 1, 2, 2, 3, 3,..., (iv) 11, 22, 33,..., (v), , 1 1 1, , , , ..., 2 3 4, , (vi) 2, 22, 23, 24, ..., , (vii), , 3 , 12 ,, , 27 ,, , 48 , ..., , 2. Justify whether it is true to say that –1, –, , 3, 5, , –2,, ,... forms an AP as, 2, 2, , a 2 – a1 = a3 – a2., , 3. For the AP: –3, –7, –11, ..., can we find directly a30 – a20 without actually finding, a 30 and a20 ? Give reasons for your answer., , 4. Two APs have the same common difference. The first term of one AP is 2 and, that of the other is 7. The difference between their 10th terms is the same as the, difference between their 21st terms, which is the same as the difference between, any two corresponding terms. Why?, , 5. Is 0 a term of the AP: 31, 28, 25, ...? Justify your answer., , 6. The taxi fare after each km, when the fare is Rs 15 for the first km and Rs 8 for, each additional km, does not form an AP as the total fare (in Rs) after each, km is, 15, 8, 8, 8, ..., , Is the statement true? Give reasons., , no, , 7. In which of the following situations, do the lists of numbers involved form an AP?, Give reasons for your answers., (i) The fee charged from a student every month by a school for the whole session, when the monthly fee is Rs 400.

Page 7 :
50, , EXEMPLAR PROBLEMS, , (ii) The fee charged every month by a school from Classes I to XII, when the, monthly fee for Class I is Rs 250, and it increases by Rs 50 for the next higher, class., , tt ©, o N, be C, re ER, pu T, bl, is, he, d, , (iii) The amount of money in the account of Varun at the end of every year when, Rs 1000 is deposited at simple interest of 10% per annum., (iv) The number of bacteria in a certain food item after each second, when they, double in every second., , 8. Justify whether it is true to say that the following are the n th terms of an AP., (i) 2n–3, , (ii) 3n2 +5, , (iii) 1+n+n2, , (D) Short Answer Questions, , Sample Question 1 : If the numbers n – 2, 4n – 1 and 5n + 2 are in AP, find the, value of n., Solution :, , As n – 2, 4n – 1, 5n + 2 are in AP,, , so, , (4n – 1) – (n – 2) = (5n + 2) – (4n – 1), , i.e,, , 3n + 1 = n + 3, , i.e,, , n=1, , Sample Question 2 : Find the value of the middle most term (s) of the AP :, –11, –7, –3,..., 49., Solution :, , Here, a = –11, d = –7 – (–11) = 4, a n = 49, , We have an = a + (n – 1) d, , So,, , 49 = –11 + (n – 1) × 4, , i.e., 60 = (n – 1) × 4, n = 16, , no, , i.e.,, , As n is an even number, there will be two middle terms which are, 16, ⎛ 16 ⎞, th and ⎜ + 1⎟ th, i.e., the 8th term and the 9th term., 2, ⎝ 2 ⎠

Page 8 :
ARITHMETIC PROGRESSIONS, , 51, , a 8 = a + 7d = –11 + 7 × 4 = 17, a 9 = a + 8d = –11 + 8 × 4 = 21, So, the values of the two middle most terms are 17 and 21, respectively., , tt ©, o N, be C, re ER, pu T, bl, is, he, d, , Sample Question 3: The sum of the first three terms of an AP is 33. If the product of, the first and the third term exceeds the second term by 29, find the AP., Solution : Let the three terms in AP be, a – d, a, a + d., , So,, , a – d + a + a + d = 33, , or, , a = 11, , Also,, , (a – d) (a + d) = a + 29, , i.e.,, , a 2 – d 2 = a + 29, , i.e.,, , 121 – d 2 = 11 + 29, , i.e.,, , d 2 = 81, , i.e.,, , d=±9, , So there will be two APs and they are : 2, 11, 20, ..., and 20, 11, 2, ..., , EXERCISE 5.3, , 1. Match the APs given in column A with suitable common differences given in, column B., Column A, , Column B, , 2, – 2, – 6, – 10,..., , (A2 ), , a = –18, n = 10, a n = 0, , (B 2), , –5, , (A3 ), , a = 0, a 10 = 6, , (B 3), , 4, , (A4 ), , a 2 = 13, a4 =3, , (B 4), , –4, , (B 5), , 2, , no, , (A1 ), , (B 1), , (B6), , 1, 2, , (B7) 5, , 2, 3

Page 9 :
52, , EXEMPLAR PROBLEMS, , 2. Verify that each of the following is an AP, and then write its next three terms., (i) 0,, , 1 1 3, , , ,..., 4 2 4, 14 13, ,, , 4,..., 3 3, , (iii), , 3 , 2 3 , 3 3 ,..., , tt ©, o N, be C, re ER, pu T, bl, is, he, d, (ii) 5,, , (iv) a + b, (a + 1) + b, (a + 1) + (b + 1), ..., (v) a, 2a + 1, 3a + 2, 4a + 3,..., , 3. Write the first three terms of the APs when a and d are as given below:, (i) a =, , 1, 1, , d= –, 2, 6, , (ii) a = –5, d = –3, , (iii) a =, , 2,, , d=, , 1, 2, , 4. Find a, b and c such that the following numbers are in AP: a, 7, b, 23, c., , 5. Determine the AP whose fifth term is 19 and the difference of the eighth term, from the thirteenth term is 20., 6. The 26th, 11th and the last term of an AP are 0, 3 and –, , 1, , respectively. Find the, 5, , common difference and the number of terms., , 7. The sum of the 5th and the 7th terms of an AP is 52 and the 10th term is 46. Find the, AP., , no, , 8. Find the 20th term of the AP whose 7th term is 24 less than the 11 th term, first term, being 12., 9. If the 9th term of an AP is zero, prove that its 29th term is twice its 19th term., , 10. Find whether 55 is a term of the AP: 7, 10, 13,--- or not. If yes, find which term, it is.

Page 10 :
ARITHMETIC PROGRESSIONS, , 53, , 11. Determine k so that k2+ 4k + 8, 2k2 + 3k + 6, 3k2 + 4k + 4 are three consecutive, terms of an AP., 12. Split 207 into three parts such that these are in AP and the product of the two, smaller parts is 4623., , tt ©, o N, be C, re ER, pu T, bl, is, he, d, , 13. The angles of a triangle are in AP. The greatest angle is twice the least. Find all the, angles of the triangle., 14. If the nth terms of the two APs: 9, 7, 5, ... and 24, 21, 18,... are the same, find the, value of n. Also find that term., , 15. If sum of the 3rd and the 8th terms of an AP is 7 and the sum of the 7th and the 14th, terms is –3, find the 10th term., , 16. Find the 12th term from the end of the AP: –2, –4, –6,..., –100., 17. Which term of the AP: 53, 48, 43,... is the first negative term?, , 18. How many numbers lie between 10 and 300, which when divided by 4 leave a, remainder 3?, 19. Find the sum of the two middle most terms of the AP: –, , 4, 2, 1, , –1, – ,..., 4 ., 3, 3, 3, , 20. The first term of an AP is –5 and the last term is 45. If the sum of the terms of the, AP is 120, then find the number of terms and the common difference., 21. Find the sum:, , (i) 1 + (–2) + (–5) + (–8) + ... + (–236), , 1, 2, 3, + 4 –, + 4 –, +... upto n terms, n, n, n, , (ii), , 4–, , (iii), , a – b 3a – 2b 5a – 3b, +, +, + ... to 11 terms., a +b, a+ b, a +b, , no, , 22. Which term of the AP: –2, –7, –12,... will be –77? Find the sum of this AP upto the, term –77., 23. If a n = 3 – 4n, show that a1 , a2 , a3 ,... form an AP. Also find S20 ., , 24. In an AP, if Sn = n (4n + 1), find the AP.

Page 11 :
54, , EXEMPLAR PROBLEMS, , 25. In an AP, if Sn = 3n2 + 5n and a k = 164, find the value of k., 26. If Sn denotes the sum of first n terms of an AP, prove that, S12 = 3(S8 –S4), , tt ©, o N, be C, re ER, pu T, bl, is, he, d, , 27. Find the sum of first 17 terms of an AP whose 4th and 9th terms are –15 and –30, respectively., , 28. If sum of first 6 terms of an AP is 36 and that of the first 16 terms is 256, find the, sum of first 10 terms., 29. Find the sum of all the 11 terms of an AP whose middle most term is 30., 30. Find the sum of last ten terms of the AP: 8, 10, 12,---, 126., , 31. Find the sum of first seven numbers which are multiples of 2 as well as of 9., [Hint: Take the LCM of 2 and 9], , 32. How many terms of the AP: –15, –13, –11,--- are needed to make the sum –55?, Explain the reason for double answer., , 33. The sum of the first n terms of an AP whose first term is 8 and the common, difference is 20 is equal to the sum of first 2n terms of another AP whose first term, is – 30 and the common difference is 8. Find n., , 34. Kanika was given her pocket money on Jan 1st, 2008. She puts Re 1 on Day 1,, Rs 2 on Day 2, Rs 3 on Day 3, and continued doing so till the end of the month,, from this money into her piggy bank. She also spent Rs 204 of her pocket money,, and found that at the end of the month she still had Rs 100 with her. How much, was her pocket money for the month?, 35. Yasmeen saves Rs 32 during the first month, Rs 36 in the second month and, Rs 40 in the third month. If she continues to save in this manner, in how many, months will she save Rs 2000?, , (E) Long Answer Questions, , no, , Sample Question 1: The sum of four consecutive numbers in an AP is 32 and the, ratio of the product of the first and the last terms to the product of the two middle terms, is 7 : 15. Find the numbers., Solution: Let the four consecutive numbers in AP be, a –3d, a – d, a + d, a + 3d.

Page 12 :
ARITHMETIC PROGRESSIONS, , So,, , 55, , a –3d + a – d + a + d + a + 3d = 32, or, , 4a = 32, , or, , a=8, , Also,, , a –3d a 3d, a–d a d, , or,, , a2 – 9d 2 7, a2 – d 2 15, , or,, , 15 a 2 – 135 d 2 = 7a2 – 7 d 2, , or,, , 8 a2 – 128 d 2 = 0, , or,, , d2 =, , or,, , d=±2, , tt ©, o N, be C, re ER, pu T, bl, is, he, d, , 7, 15, , 8 8 8, 4, 128, , So, when a = 8, d = 2, the numbers are 2, 6, 10, 14., , Sample Question 2: Solve the equation :, 1 + 4 + 7 + 10 +...+ x =287, , Solution :, , Here, 1, 4, 7, 10, ..., x form an AP with a = 1, d = 3, an = x, We have, an = a + (n – 1)d, , x = 1 + (n – 1) × 3 = 3n – 2, , Also,, , S=, , So,, , 287 =, , no, , So,, , n, ( a l), 2, , n, (1 x ), 2

Page 13 :
56, , EXEMPLAR PROBLEMS, , =, , n, (1 3n – 2), 2, , 574 = n (3n – 1), , or,, , 3n 2 – n – 574 = 0, , tt ©, o N, be C, re ER, pu T, bl, is, he, d, , or,, , Therefore, n =, , =, , 1, , 1 6888, 6, , 1 ± 83 84 –82, = ,, 6, 6 6, , = 14,, , – 41, 3, , As n cannot be negative, so n = 14, , Therefore, x = 3n – 2 = 3 × 14 – 2 = 40., Alternative solution:, , Here, 1, 4, 7, 10, ... x form an AP with a = 1, d = 3, S = 287, We have, S=, , So, 287, , n, 2, 2, , n, 2a, 2, , n –1 d, , n –1 3, , or, 574 n (3n – 1), or, 3n 2 – n – 574 0, , no, , Now proceed as above., , EXERCISE 5.4, , 1. The sum of the first five terms of an AP and the sum of the first seven terms of the, same AP is 167. If the sum of the first ten terms of this AP is 235, find the sum of, its first twenty terms.

Page 14 :
ARITHMETIC PROGRESSIONS, , 57, , 2. Find the, (i) sum of those integers between 1 and 500 which are multiples of 2 as well as of 5., (ii) sum of those integers from 1 to 500 which are multiples of 2 as well as of 5 ., , tt ©, o N, be C, re ER, pu T, bl, is, he, d, , (iii) sum of those integers from 1 to 500 which are multiples of 2 or 5., [Hint (iii) : These numbers will be : multiples of 2 + multiples of 5 – multiples of 2, as well as of 5 ], , 3. The eighth term of an AP is half its second term and the eleventh term exceeds, one third of its fourth term by 1. Find the 15th term., , 4. An AP consists of 37 terms. The sum of the three middle most terms is 225 and the, sum of the last three is 429. Find the AP., 5. Find the sum of the integers between 100 and 200 that are, (i) divisible by 9, , (ii) not divisible by 9, , [Hint (ii) : These numbers will be : Total numbers – Total numbers divisible by 9], , 6. The ratio of the 11 th term to the 18th term of an AP is 2 : 3. Find the ratio of the 5th, term to the 21st term, and also the ratio of the sum of the first five terms to the sum, of the first 21 terms., , 7. Show that the sum of an AP whose first term is a, the second term b and the last, term c, is equal to, a c b c – 2a, 2 b –a, , no, , 8. Solve the equation, , – 4 + (–1) + 2 +...+ x = 437, , 9. Jaspal Singh repays his total loan of Rs 118000 by paying every month starting, with the first instalment of Rs 1000. If he increases the instalment by Rs 100 every, month, what amount will be paid by him in the 30th instalment? What amount of, loan does he still have to pay after the 30th instalment?

Page 15 :
58, , EXEMPLAR PROBLEMS, , no, , tt ©, o N, be C, re ER, pu T, bl, is, he, d, , 10. The students of a school decided to beautify the school on the Annual Day by, fixing colourful flags on the straight passage of the school. They have 27 flags, to be fixed at intervals of every 2 m. The flags are stored at the position of the, middle most flag. Ruchi was given the responsibility of placing the flags. Ruchi, kept her books where the flags were stored. She could carry only one flag at a, time. How much distance did she cover in completing this job and returning, back to collect her books? What is the maximum distance she travelled carrying, a flag?