Page 1 :
1. Angle and its measurement, (1) Find the radian measure of the angle between hour-hand and minutehand of a clock at :, (i) Twenty minutes past two , (ii) Ten minutes past eleven, (iii) Thirty minutes past six , (iv) Five minutes past one, Solution : The speed of minute hand is 6° per minute. The speed of, the hour hand is 0.5° per minute. The angle between hour hand and, minute hand changes at the rate 5.5°., (i) Twenty minutes past two : 2:20, We consider two positions of, hands. First at 2:00 and second, at 2:20., At 2:00 angle between them, is 60°. This angle gradually, decreases, becomes zero and, then increases. From 2:00 to, 2:20 (i.e. in 20 minute time), the minute hand moves through, 120° and hour hand moves, through 20 × 0.5° = 10°., The minute hand makes 120°, - 60° = 60° angle with the, position of hour hand at 2:00., But hour hand has moved, through 10°. The required angle, is 60° - 10° = 50°., (ii) Ten minutes past eleven : 11:10, , 1
Page 2 :
(iii) Thirty minutes past six : 6 : 30, , (iv) Five minutes past one : 1 : 05, , 2
Page 3 :
(2) Find the exact time when the angle between hour-hand and the, minute-hand of a clock will be : (i) 44° for the first time after 12, O’clock. (ii) 59° for the first time after 6 O’clock., Solution : The angle between hour hand and minute hand changes at, the rate 5.5°., The angle between them will be 11° after 2 minutes., (i) For 11° angle it takes 2 minute time. How much time will it take, for 44° angle ? 2 � 44 � 8, 11, , ∴ At 12:08 the angle between hour-hand and the minute-hand of a, clock will be 44° for the first time after 12 O’clock., (ii) 59° for the first time after 6 O’clock., Solution :, , (3) A wire of length 10 cm is bent to form an arc of a circle of radius, 4 cm. Find the radian and degree measure of the angle subtended, by the arc at the center of the circle. Also find the area of the, corresponding sector., 3
Page 4 :
Solution : Given r = 4, arc length = length of the wire = s = 10, We know that s � r � �, ∴ ....... � 4 � �, ∴ � � ..... radian., 1, 2, , 1, 2, , 1, 2, , 2, Now, the area of the sector = A= r � � r � ....... � � 4 � ....... � ........ sq.cm., , (4), , Arrange following angles in ascending order : π°, π , 3 , 100°, π, 2, 0, , Solution :, , 4, , c, , c
Page 5 :
(5) ABCDEFGH is a regular octagon inscribed in a circle of radius 1, unit. O is the center of the circle. Find, (i) Radian measure of ∠AOB (ii) l � chord � AB � (iii) l � arc � AB �, (iv) Area of the region enclosed between chord AB and arc AB., Solution : Draw AK perpendicular to, OB., Given OA = OB = 1 Find AK,, OK, BK and then AB., , 5
Page 6 :
(6) Prove that the lateral surface area of a right circular cone is πrl,, where r is the radius of the circular base and l is the slant height, of the cone., Solution :, , 6
Page 7 :
2. Trigonometry, (1) Construct an angle in standard position whose terminal arm passes, through A(-6, 8). Hence find all trigonometric ratios of this angle., Solution :, , OA � r � (�6) 2 � (8) 2 � 100 � 10, , A � (�6, 8) � (x, y), , A, , 8, 6, , � x � �6 and y � 8, , 4, , Let measure of �XOA be � ., , 2, , y 8 4, � �, r 10 5, x �6, 3, cos � � �, ��, r 10, 5, y 8, 4, tan � � �, ��, 3, x �6, , sin � �, , 1, 5 -8 -6 -4 -2 0 O 2, �, -2, sin � 4, 1, 5, -4, sec� �, ��, co �, 3, 1, 3, ��, cot� �, tan �, 4, , cosec� �, , 4, , 6, , X, , (2) Construct angle of measure 22.5° by bisecting angle of measure 45°., Hence find the value of tan 22.5°, B, , Solution : Let ∆ OAB be an, isosceles right angle triangle, and OA= AB = 1., 2, , ∴ OB= 2, , 1, , Draw bisector of angle AOB., Let it intersect AB in C., m�AOC � 22.50, , O, , Note that C is not the mid, point of AB., , 1, , A, B, , Use section formula to find, length of AC., Use Pythagoras theorem to find, OC. Then write trigonometric, ratios of angle 22.50 . Write, your calculations here., , 2, , O, 7, , C, , 1, , A
Page 8 :
(3) Draw and measure the angle in standard position whose tangent ratio, is, , 7, ., 13, , Let θ be the measure of one of the angles having tangent, , Solution :, ratio, , 7, 13, y, , 7, , As tan � � � , the terminal arm of the angle passes through A(13, 7), x 13, Now draw angle in standard position whose terminal arm passes, through A(13,7). Using protractor measure the angle XOA., , 8
Page 9 :
(4) Draw and estimate the angle in standard position whose sine ratio, is 0.57., Solution :, , 9
Page 10 :
(5) (a) Which is greater sin �18560 � or sin � 20190 � ? Give reason., (b) Which of the following is positive ? sin � �3100 � or sin � 3100 � ? Give, reason., Solution :, , 10
Page 11 :
(6) Construct a triangle, the measures of whose angles are 320 , 580 and 900 ., Measure the lengths of sides of this triangle. Find sin 320 and cos 320 ., Hence find the value of sin232° + cos232°., Solution : Construct ∆ ABC with A = 32°, B = 90°, C = 58°., , 11
Page 12 :
3. Trigonometry, (1) Show that � cos � � i sin � � � cos 3� � i sin 3�, 3, , Solution : We know that (a � b)3 � a 3 � 3a 2b � 3ab 2 � b3, L. H. S = � cos � � i sin � � � cos3 � � 3 cos 2 � (i sin � ) � 3 cos � (i sin � )2 � (i sin � )3, 3, , , , � � cos3 � � 3 cos � sin 2 � � � i � 3 cos 2 � sin � � sin 3 � �, , , , � � cos3 � � 3 cos � (1 � cos 2 � ) � � i � 3(1 � sin 2 � ) sin � � sin 3 � �, , , , � � cos3 � � 3 cos � � 3 cos3 � � � i � 3 sin � � 3 sin 3 � � sin 3 � �, , , , � � 4 cos3 � � 3 cos � � � i � 3 sin � � 4 sin 3 � �, , , , � cos 3� � i sin 3�, , ∴, , � cos � � i sin � �, , 3, , � cos 3� � i sin 3�, , (2) Show that cos 3� � sin 3� � � cos � � sin � � �1 � 2 sin 2� �, Solution : L.H.S. = cos 3� � sin 3�, , 12
Page 13 :
(3) Prove that cos 2 � � cos 2 �� � 1200 � � cos 2 �� � 1200 � �, , 3, 2, , Solution : We know that cos � A � 2700 � � sin A and cos � A � 2700 � � � sin A, L.H.S. = cos 2 � � cos 2 �� � 1200 � � cos 2 �� � 1200 �, �, , 1, � 2 cos 2 � � 2 cos 2 �� � 1200 � � 2 cos 2 �� � 1200 � �, �, 2�, , �, , 1, �1 � cos � 2� � � 1 � cos � 2� � 2400 � � 1 � cos � 2� � 2400 � �, �, 2�, , �, , 1, �3 � cos � 2� � � cos � 2� � 300 � 2700 � � cos � 2� � 300 � 2700 � �, �, 2�, , �, , 1, �3 � cos � 2� � � sin � 2� � 300 � � sin � 2� � 300 � �, �, 2�, , �, , 1, �3 � cos � 2� � � sin � 2� � 300 � � sin � 2� � 300 � �, �, 2�, , (4) If A � B � C � � then prove that cos 2 A � cos 2 B � cos 2C � 1 � 2cosA cosB cosC., 1, 2, 2, L.H.S. = cos A + cos 2 B + cos 2 C, , Hence prove that cos 600 = ., Solution :, �, , 1, 2 cos 2 A � 2 cos 2 B � 2 cos 2 C �, �, 2, , 13
Page 14 :
1, �1 � cos 2 A� 1 � cos 2B � 2 cos2 C �, 2, , �, , 1, � 2 � cos 2 A� cos 2B � 2 cos2 C �, 2, , �, , 1, 2 � 2 cos( A � B) cos(..........) � 2 cos 2 C �, �, 2, , �, , 1, 2 � 2 cos(.... � C ) cos( A � B) � 2 cos 2 C �, �, 2, , �, , 1, 2 � 2 cos C cos( A � B) � 2 cos 2 C �, �, 2, , �, , 1, � 2 � 2 cos C �cos( A � B) � cos C ��, 2, , �, , 1, � 2 � 2 cos C �cos( A � B) � cos(........)��, 2, , �, , 1, � 2 � 4 cos C cos A cos B �, 2, , � 1 � 2 cos A cos B cos C, , = R.H.S., In the above take A= B= C = 600, , and find the value of cos 600 ., , (5) Find the values of sin180 and cos180 ., Solution :, , 14
Page 15 :
(6) If tan A =, , �, 5, 1, and tan B =, then show that A � B � ., 6, 11, 4, 15
Page 16 :
Solution :, , 16
Page 17 :
4. Determinants and Matrices, � cos �, , sin � �, , (1) If A � �, � then show that, � � sin � cos � �, � cos 2�, � � sin 2�, , (i) A2 � �, Solution :, , sin 2� �, cos 2� ��, , (i) Given ,, , � cos �, � A 2 � A.A � �, � � sin �, , � cos�, A��, � � sin�, , � cos 2�, � A2 � �, � � sin 2�, , sin 3� �, cos 3� ��, , sin� �, cos� ��, , sin � � � cos �, �, cos � �� �� � sin �, , � cos � cos � � sin � � � sin � �, � A2 � �, �� � sin � � cos � � cos � � � sin � �, , �cos 2 � � sin 2 �, � A2 � �, � �2 sin � cos �, , � cos 3�, � � sin 3�, , (ii) A3 � �, , sin � �, cos � ��, , cos � sin � � sin � cos � �, � � sin � � sin � � cos � cos � ��, , 2 sin � cos � �, �, cos 2 � � sin 2 � �, , sin 2� �, - - - - - - - - - - - - - - - - (1), cos 2� ��, , (ii) We know that, � cos 2�, � A3 � �, � � sin 2�, , A 3 = A 2 .A, , sin 2� � � cos�, �, cos 2� �� �� � sin�, , � cos 2� cos� � sin 2� sin�, � A3 � �, � � sin 2� cos� � cos 2� sin�, , sin� �, from, cos� ��, , equation, , (1) we get., , cos 2� sin� � sin 2� cos� �, = ........, � sin 2� sin� � cos 2� cos� ��, , (2) Construct a 3 × 3 matrix A � �� aij �� whose elements are given by :, (i) aij � i � j, (iii), , �0, if, aij � �, �1, if, , Solution :, , , , , , i� j, i� j, , (ii) aij � � i � j �, (iv), , 2, , � 0, if i � j, �, aij � � 1, if i � j, ��1, if i � j, �, , 2, 3. j 1, 2, 3., (i) aij � i � j =, , i 1,=, , a11 � 1�1 � 1, , ,, , a12 � 1� 2 � 2 ,, , a21 � 2 �1 � 2 , a22 � 2 � 2 � 4 ,, , a13 � 1� 3 � 3, a23 � 2 � 3 � 6, , a31 � 3 �1 � 3 , a32 � 3 � 2 � 6 , a33 � 3 � 3 � 9, 17
Page 18 :
1 2 3�, Thus , A � � 2 4 6 �, �, �, �� 3 6 9 ��, , 2, 3. j 1, 2, 3., j � , i 1,=, (ii) aij � � i � =, 2, , a11 � �1 � 1� � 22 � 4, 2, , 2, , a12 � �1 ��� � .... � ..., , a21 � ���� 1� � � � �, , a22 � ������, �, � ��, 2, , 2, , =, a31 ............., = ......... =, a32 ............., = ........., ∴, , a13 � �1 ��.� � � � �, , 2, , =, a33 ............., = ........., , � 4 9 16 �, A � ��� � ���, ��� � ���, , �0, if, �1, if, , (iii) aij � �, , i� j, i� j, , � 0, if i � j, �, (iv) aij � � 1, if i � j, ��1, if i � j, �, , for, , i = 1, 2, 3., , 18, , =, a23 ............., = ........., , j = 1, 2, 3.
Page 19 :
1 a bc, (3) Using properties of determinants show that 1 b ca � � a � b � � b � c � � c � a �, 1 c ab, , Solution :, , Consider, By, , using, , 1 a bc, L.H .S . = 1 b ca, 1 c ab, R2 − R1, , and, , R3 − R1, , 1, a, bc, � 0 b � a ca � bc, 0 c � a ab � bc, 1, a, bc, � 0 � � a ��� c � a ���, 0, c�a, �b � c ���, , By taking � a � b � common from R and � c � a � common from R3, 2, we get, 1 a bc, L.H .S . � � a � b � � c � a � 0 ... ..., 0 1 ..., 19
Page 20 :
By using R3 + R2, 1, L.H .S . � � a � b � � c � a � 0, , a bc, �1 c, , ... ... ....., L.H .S . � � a � b � � c � a � ��1� � �1� � c � b � � 0 � � a � 0 � 0 � � bc � 0 � 0 � ��, L.H .S . � � a � b � � c � a � �������..�, L.H .S . � � a � b � � b � c � � c � a �, , (4) Using properties of determinants show that, 1� a, 1, 1, 1 1� b, 1 � abc � ab � bc � ca, 1, 1 1� c, , Solution :, , 20
Page 21 :
x, (5) If x ≠ y ≠ z and y, z, , x 2 1 � x3, y 2 1 � y 3 � 0 then show that 1 � xyz � 0 ., z 2 1 � z3, , Solution :, , (6) Using properties of determinants show that, a �b�c, 2a, 2a, 3, 2b, b�c�a, 2b, � �a � b � c�, 2c, 2c, c�a �b, , 21
Page 22 :
Solution :, , 22
Page 23 :
5. Straight Lines, (1) Show that the equation of the line passing through A � x1 , y1 � and, parallel to the line ax � by � c � 0 is a � x � x1 � � b � y � y1 � � 0 . Hence find, the equation of the line passing through �1,1� and parallel to the line, 15 x � 8 y � 1947 � 0 ., Solution :, , Slope of the line ax � by � c � 0 is − a ., b, , Required line is parallel to this line., a, ∴ The slope of the required line is also − . And it passes through, b, A � x1 , y1 � ., a, b, , The equation of the required line is y � y1 � � � x � x1 �, ∴ by � by1 � � ax � ax1, ∴ a � x � x1 � � b � y � y1 � � 0, , Now the equation of the line parallel to 15 x � 8 y � 1947 � 0 and passing, through (1, 1) is, 15 � x � 1� � 8 � y � 1� � 0, ∴ 15 x � 8 y � 23 � 0, , (2) Show that the equation of the line having slope m and making, x-intercept d is given by y � m � x � d � . Find the y-intercept of this, line., Solution :, , The x -intercept of the line is d . Therefore it cuts the X, , axis in �....,....� ., Slope of the line is m ., ∴ It’s equation of the line is, , � y � .....� � �� x � � ......�, , ∴ ………………………………………………………………., ∴ ………………………………………………………………., , To find it’s y-intercept., , 23
Page 24 :
(3) A line makes intercepts h and k on the co-ordinate axes. If p is, the length of the perpendicular drawn from the origin to the line, then show that, , 1, 1, 1, � 2 � 2., 2, h, k, p, , Solution : Line makes intercepts h and k on the co-ordinate axes. Its, x y, � � 1., h k, kx � hy � hk � 0, , equation is, , The length of the perpendicular drawn from the origin to the line, kx � hy � hk � 0 is, p�, , ���., k 2 � h2, , �, , �, , ∴ p 2 k 2 � h 2 � ........., h2 � k 2, 1, ∴, � 2, ��� p, , ∴, , 1, 1, 1, � 2 � 2., 2, h, k, p, , (4) Show that there are two lines which pass through the point A � 3, 7 �, and the sum of whose intercepts on the co-ordinate axes is zero., Draw the rough sketch of these two lines. Solution :, , Let slope of one of the lines be m ., , Its equation is y � 7 � m � x � 3�, mx � y � � 7 � 3m � � 0, , Intercepts made by this line on the co-ordinate axes are ……….., 24
Page 25 :
and, , …….., , Their sum is …………., But it is given that the sum of intercepts is zero., ∴ ………………….= 0, ∴ ………………………………., ∴ ………………………………………, ∴ m = ……., , Or m = ………., , As m has two values, there are two lines., Their, equations, are, ……………………………, , …………………………………, , and, , Rough sketch :, , (5) Find the number of lines which pass through the point B � 5, 5 � and, the sum of whose intercepts on the co-ordinate axes is zero., Solution :, , 25
Page 26 :
(6) Find the co-ordinates of the orthocenter of the triangle formed by, lines 2 x � y � 9 � 0 , x � 2 y � 9 � 0 and x � y � 9 � 0 ., Solution :, , 26
Page 27 :
27
Page 28 :
6. Circle and Parabola, (1) Find the center and radius of the circle x 2 � y 2 � x � 2 y � 3 � 0, Solution : We know that the center of the circle x 2 � y 2 � 2 gx � 2 fy � c � 0, is � � g ,� � f � and its radius is r � g 2 � f 2 � c, Comparing given equation with, , x 2 � y 2 � 2 gx � 2 fy � c � 0, , we get,, , 1, g � � , f � 1 , c � �3, 2, 2, �, �1, ∴ center is � , �1� and radius r � �� � 1 �� � �1�2 � � �3� � 1 � 1 � 3 � 17, �, �2, 4, 2, � 2�, , unit., , 2), , Find the equation of circle passing through the point of intersection, of the lines x � 3 y � 0 and 2 x � 7 y � 0 and whose centre is the point, of intersection of the lines x � y � 1 � 0 and x � 2 y � 4 � 0 ., , Solution : The point of intersection of x � 3 y � 0 and 2 x � 7 y � 0 is (0, 0), { How ?}, Solving x � y � 1 � 0 and x � 2 y � 4 � 0 we get ,, their point of intersection., , (……., …….) as, , The center of the circle is ………. and it passes through …………….., ∴ Its radius is, , The equation of the circle is ……………………………………………, , 3), , Find the equation of circle, the end points of whose diameter are, the centers of circles x 2 � y 2 � 6 x � 14 y � 1 � 0 and x 2 � y 2 � 4 x � 10 y � 2 � 0 ., , Solution : The center of the circle x 2 � y 2 � 6 x � 14 y � 1 � 0 is ……….., The center of the circle x 2 � y 2 � 4 x � 10 y � 2 � 0, 28, , is ………..
Page 29 :
The end points of the diameter of the required circle are, ……………………………………. The equation of the required circle is, ……………………………………………………………………………, , 4), , Find the equation of the circle passing through points � 5, 7 � , � 6, 6 � & � 2, �2 � ., , Solution, ……………………………………………………………………, , 5), , :, , Find the co-ordinates of the focus, equation of the directrix, length, of Latus Rectum, and the co-ordinates of the end points of the Latus, 29
Page 30 :
2, 2, 2, Rectum of the parabola i )5 y � 24 x, ii ) x � 12 y, iii )3 y � �16 x ., , Solution :, , i) 5y2 = 24x, , Comparing y 2 =, , 6, 24, 24, �a �, x with y 2 = 4ax , we get 4a =, 5, 5, 5, , The co-ordinates of the focus are � a, 0 � � �� , 0 �� ,, 5, 6, , �, , �, , Equation of the directrix is x � �a � , ∴ x � �, The length of Latus Rectum is 4a =, , 6, 5, , ∴ 5x � 6 � 0, , 24, 5, , The co-ordinates of the end points of the Latus Rectum are � a, 2a �, 6 12, 6 12, and � a, �2a � , �� , �� and �� , � ��, 5�, �5, �5 5 �, 2, ii) x = 12y, , iii) 3y2 = 16x, , 6), , Find the co-ordinates of the focus, equation of the directrix, length, of Latus Rectum, & the co-ordinates of the end points of the Latus, 30
Page 31 :
Rectum of the parabola x 2 � 4 x � 4 y � 16 � 0 ., Solution : Rewrite equation x 2 � 4 x � 4 y � 16 � 0 as x 2 � 4 x � �4 y � 16, ∴ x 2 � 4 x � 4 � �4 y � 12, ∴, , � x � 2�, , 2, , � �4 � y � 3�, , 7), , Find the area of triangle formed by the lines joining the vertex of, the parabola x2 = 12y to the ends of its Latus rectum., Solution :, , 31
Page 32 :
8), , For which point of the parabola, 3 time the abscissa?, Solution :, , 32, , y 2 = 18 x is, , the ordinate equal to
Page 33 :
7. Ellipse and Hyperbola, (1) Find the lengths of the major and minor axes, co-ordinates of vertices,, eccentricity, co-ordinates of the foci, equations of directrices and the, length of the Latus Rectum of the following conics., (i) 9 x 2 � 16 y 2 � 144, x2 y 2, (iii) 25 � 9 � 1, , (ii), , 4 x 2 � 25 y 2 � 100, , (iv), , y 2 x2, � �1, 4, 9, , Solution :, (i) Given equation of ellipse is, i.e., , 9 x 2 � 16 y 2 � 144., , x2 y 2, �, �1, 16 9, , � a 2 � 16, , and, , b2 = =, 9 . ⇒ a 4=, and b 3, , Here a > b., Lengths of axes :Length of major axis � 2a � 2 � 4 � 8 units, Length of minor axis is � 2b � 2 � 3 � 6 units, Co-ordinates of vertices:Co-ordinates of vertices are � � a, 0 � and, i.e., � �4, 0 � and � 0, �3�, Eccentricity :e�, , � 0, �b �, , 16 � 9, 7, a 2 � b2, �, �, 4, 4, a, , Co-ordinates of the foci :�, , Co-ordinates of the foci � � � ae, 0 � � �� �4 �, �, , Equations of Directrices :Equation of directrices are, i.e., (ii), , x��, , x��, , 4, 16, ��, 7 /4, 7, , 4 x 2 � 25 y 2 � 100, , 33, , a, e, , 7 �, , 0 �� � � 7 , 0 ., 4, �
Page 34 :
(iii) Given equation of hyperbola is, � a 2 � 25, , and, , x2 y 2, �, �1, 25 9, , and b 3, b 2 = 9=, . ⇒ a 5=, , Here a > b., Lengths of axes :Length of transverse axis � 2a � 2 � 5 � 10 units, Length of conjugate axis is � 2b � 2 � 3 � 6 units, Co-ordinates of vertices:Co-ordinates of vertices are � � a, 0 �, i.e., � �5, 0 �, Eccentricity :e�, , 25 � 9, 34, a 2 � b2, �, �, 5, 5, a, , Co-ordinates of the foci :�, , Co-ordinates of the foci � � � ae, 0 � � �� �5 �, �, , Equations of Directrices :Equation of directrices are, i.e., , x��, , x��, , a, e, , 5, 25, ��, 34 / 5, 34, 34, , 34 �, , 0 �� � � 34 , 0 ., 5, �
Page 35 :
2, 2, (iv) y � x � 1, , 4, , 2), , 9, , Find the equation of ellipse referred to its principal axes with, 3, , eccentricity, and passing through the point � 6, 4 � ., 4, Solution :, Given :, , e=, , 3, , P � x1 , y1 � � � 6, 4 � ., 4, , 2, 2, Let equation of ellipse is x 2 � y2 � 1, , a, , b, , As it passes through the point P � � 6, 4 � we get, 36 16, � � 1 - - - - - - - - - - - - - - - - - - - - - - - - (1), a 2 b2, , Also b 2 � a 2 �1 � e2 �, 9�, �, � b 2 � a 2 �1 � �, � 16 �, 35
Page 36 :
7�, � b2 � a 2 � �, � 16 �, , - - - - - - - - - - - - - - - - - - (2), , ∴� � � � from equation (1) we get, 36, �, a2, , 16, �1, 2� 7 �, a � �, � 16 �, , � 36 �, , 256, � a2, 7, , � a2 �, , 252 � 256, 7, , � a2 �, , 508, 7, , Using the value of a 2 in equation (2), � b2 �, , 508 7, �, 7 16, , � b2 �, , 508, 16, , x2, y2, Thus the required equation of the ellipse is 508 � 508 � 1, 7, 16, , i.e. 7 x 2 � 16 y 2 � 508, y 2 x2, x2 y 2, e, e, 3) If 1 and 2 are eccentricities of hyperbolas 2 � 2 � 1 and 2 � 2 � 1, b, a, a, b, 1 1, then show that 2 � 2 � 1, e1 e2, x2 y 2, Solution : Let e1 be the eccentricity of hyperbola 2 � 2 � 1, a, b, � e1 �, , a 2 � b2, a, , � e12 �, , a 2 � b2, a2, , �, , 1, a2, �, e12 a 2 � b 2, , and e2, � e2 �, , � e22 �, , - - - - - - - - - - - - - - - - - - - - - (1), , be the eccentricity of hyperbola, a 2 � b2, b, , a 2 � b2, b2, 36, , y 2 x2, �, �1, b2 a 2
Page 37 :
1, b2, �, e22 a 2 � b 2, , - - - - - - - - - - - - - - - - - - - - - -, , (2), , Adding equation (1) and (2) we get, 1 1, a2, b2, �, �, �, e12 e22 a 2 � b 2 a 2 � b 2, , �, , 1 1 a 2 � b2, � 2� 2 � 2, e1 e2 a � b 2, , 1 1, � �1, e12 e22, , 4), , Find the equation of the hyperbola whose, (i) foci are at � �4, 0 � and the length of its Latus rectum is 12 unit., (ii) Vertices are � 0, �2 � and the foci are at � 0, �3� ., (iii) directrix is 2 x � y � 1, focus at �1, 2 � and eccentricity 3., Solution :, (i) Given : foci � � �4, 0 � & Length of Latus rectum = 12 unit, We have for hyperbola, , x2 y 2, �, �1, a 2 b2, , Foci � � � ae, 0 � and Length of L.R. =, � � � ae, 0 � � � �4, 0 � and, 2, � ae � 4 and b = 6a, , 2b 2, = 12, a, , 2b 2, a, , - - - - - - - - - - - - - - - - - - - - - -(1), , We have relation between a, b & e for hyperbola is b 2 � a 2 � e2 � 1�, � b 2 � � ae � � a 2, 2, , � 6a � � 4 � � a 2, 2, , � a 2 � 6a � 16 � 0, , �6 � 36 � 64, �6 � 100, � a�, 2, 2, �6 � 10, and � a � �8, � a�, �a � 2, 2, From equation (1), and, b 2 � 6 � 2 � 12, , � a�, , b 2 � 6 � � �8 � � �48 which is, , not possible, Hence, , x2 y 2, 2, ∴�, and, equation, of, hyperbola, is, �, � 1., b = 12., a =4, 2, , 4, , (ii) Given : Vertices are � 0, �2 � and the foci are at � 0, �3� ., 2, 2, We have for hyperbola y2 � x 2 � 1, , b, , a, , 37, , 12
Page 38 :
Foci � � 0, �be �, , and Vertices are, , � � 0, �be � � � 0, �3�, , and, , � � 0, �b �, , � 0, �b � � � 0, �2 �, , Hence, be = 3 and b = 2 thus b 2 = 4., �e �, , 3, 2, , We have relation between a,� b and e is a 2 � � be � � b 2, 2, , � a 2 � � 3� � � 2 � � 9 � 4 � 5, 2, , 2, , y 2 x2, � � 1., Thus equation of hyperbola is, 4, 5, , (iii) directrix is 2 x � y � 1, focus at �1, 2 � and eccentricity, , 3., , 5) An intersecting property of rectangular hyperbola., Solution : Equation of rectangular hyperbola is x� y = � k (k is non zero, 38
Page 39 :
constant) …(I), Tangent is drawn to the curve at point on it whose abscissa is ‘a’., Therefore point of contact is (a, … ), �d, , k �, , � �, Slope of tangent � � � � � at point (a, … ), � dx � x � �, � �k �, � � 2 � at point (a, … ), �x �, k, � � 2 … . . . . . . . . . . . . . . . .(II), a, , Equation of tangent to xy �� = k, at point (a, … ) is (by slope, point form), � k �, y � ......... � � � 2 � � x � a �, � a �, , i.e. a 2 � y � .........� � �k � x � a �, i.e. …………, i.e. …………, This equation of tangent in, terms of double intercept form, is, , x, y, �, � 1., 2a 2k, a, , Tangent cuts the X – axis at point P and the Y – axis at point Q., Clearly P = (… , 0) and Q = (0, …), 1, 2, , Area of �POQ � � OP �� OQ �, �, , 6), , 1, ��.� ��.�, 2, , = 2k, , Find the focal distance of the point P � 5, 4 3 � on the ellipse, 16 x 2 � 25 y 2 � 1600., , Solution :, , 39
Page 40 :
40
Page 41 :
8. Measures of Dispersion, (1) Compute the range of the following data :, 710, 635, 423, 221, 971, 843, 307, 289., Solution :, , Smallest Value = S = ………., , Largest Value = L = …………….., Range = L – S = ……………………, , (2) Calculate the range of the following data :, Marks, No. of Students, , 0-10 10-20 20-30 30-40 40-50, 4, 17, 22, 16, 11, , Solution : L = Upper limit of highest class = ………, , , S = Lower limit of lowest class = ……….., , ∴ Range = L – S = ……. – ……… = ……., (3) A die is rolled 30 times and the following distribution is obtained., Find the variance and the standard deviation., Score, Frequency, , 1, 2, , 2, 6, , 3, 2, , 4, 5, , 5, 9, , Solution :, x, 1, 2, 3, 4, 5, 6, , f, 2, 6, 2, 5, 9, 6, , fx, , 41, , fx2, , 6, 6
Page 42 :
Repeat the experiment and construct the frequency table as shown, above. Find its mean and standard deviation., , 42
Page 43 :
(4) Find the mean and the standard deviation of the first n natural, numbers. Hence find the mean and the standard deviation of the, first 200 natural numbers., Solution :, , (5) The following table shows weight of students of two classes., Calculate the coefficient of variation of the two distributions. Also, find the mean and the standard deviation for both the classes., Weight in Kg. Class A Class B, 30-40, 8, 9, 40-50, 16, 12, 50-60, 12, 18, Solution :, , 43
Page 44 :
(6) The means of two samples of sizes 10 and 20 are 24 and 45, respectively and the standard deviations are 6 and 11. Obtain the, standard deviation of the sample of size 30 obtained by combining, the two samples., Solution :, , 44
Page 45 :
45
Page 46 :
9. Probability, (1) The turnout of spectators at the world cup cricket match is independent, upon the weather. On a rainy day the probability of a big turnout is, 0.3. If it doesn’t rain, then the probability of big turnout increases, by 0.6. The weather forecast gives a probability of 0.75 that it will, rain on the day of the match., Find the probability that (i) There is a big turn out and it rains (ii), There is a big turnout., Solution : Let R = It rains,, R’ = It doesn’t rain, B = Big turnout,, B = No big turnout., P(R) = 0.75,, P(R’) = 0.25, P(B/R) = 0.3, P(B/R’) = 0.9, (i) P(B∩R) = P(B/R).P(R), , = 0.3 × 0.75 = 0.225, (ii) P(B) = P(B/R).P(R) + P(B/R').P(R'), , = 0.3 × 0.75 + 0.25 × 0.9 = 0.45, (2) A bag contains 7 red and 5 blue balls. A ball is taken at random, from the bag, its color is noted and not replaced in to the bag. Now, a second ball is taken from the bag and its color is noted. Find the, probability that one is red and the other is blue., Solution : Let A be the event that in the first draw we get a red ball., ∴ A’ is the event that in the first draw we do not get a red ball, (i.e. we get blue ball), Let B be the event that in the second draw we get a red ball., ∴ B’ is the event that in the second draw we do not get a red ball, (i.e. we get blue ball), To find P ��� A � B� � � � A� � B ���, P ��� A � B� � � � A� � B � �� = � P � A � B� � � P � A� � B �, � P � A � P � B� / A � � P � A� � P � B / A� �, 46
Page 47 :
7 5 5 7, 70 35, � � � �, �, 12 11 12 11 132 66, , 1, 2, 1, then find :, and P � A � B � �, 4, 5, 2, 1) P � A � B � 2) P � A � B� � 3) � A� � B � 4) P � A� � B� � 5) P � A� � B� �, , (3) If P � A � � , P � B � �, , Solution : We know that P � A � B � � P � A � � P � B � � P � A � B �, ∴ 1 � ���� P � A � B �, 2, ∴ P � A � B� � �, P � A� � � 1 �� � �, , and P � B� � � 1 �� � �, , 1) P � A � B � � �� � � �, 2) P � A � B� � � �, 3) P � A� � B � � �, 4) P � A� � B� � � �, 5) P � A '� B '� � �, (4) A coin is tossed until a head appears or until it has been tossed, three times. Given that head does not occur on the first toss, what, is the probability that coin is tossed three times ?, Solution :, , 47
Page 48 :
(5) From a group of 8 boys and 5 girls, a committee of 5 is to be, formed. Find the probability that a committee contains, i) 3 boys and 2 girls ii) at least 3 boys., Solution :, , 48
Page 49 :
(6) Letters in the word AHMEDNAGAR are rearranged. Find the, probability that, (i) the arrangement begins and ends with A., (ii) the arrangement begins with A but does not end with A, (iii) no two A’s in the arrangement are adjacent to each other., Solution :, , 49
Page 50 :
10. Complex Numbers, (1) If z = 3 + 4i then show the following on the Argand diagram, (a) z, , (b), , −z, , (c) z , , (d) −z, , Solution :, 4, 3, 2, 1, -6 -5, , -4, , -3, , -2 -1 0, -1, , 1, , 2, , 3, , 4, , 5, , 6, , -2, -3, -4, , 2), , If z1 = 2 + 3i and z2 = 2 - 4i then show the following on the, Argand diagram (a) z1 (b) z2, (c) z1 + z2, (d) z1 - z2, , Solution :, 4, 3, 2, 1, -7 -6 -5 -4 -3 -2 -1 0, -1, -2, -3, -4, , 50, , 1, , 2, , 3, , 4, , 5, , 6, , 7
Page 51 :
3), , If z1 = 1 + 2i and z2 = 3 + i. Show the following on the Argand, diagram (a) z1, , (b) z2, , (c) z1 . z2 , , z1, z2, , (d), , Solution :, 4, 3, 2, 1, -7, , -6, , -5, , -4 -3, , -2 -1 0, -1, , 1, , 2, , 3, , 4, , 5, , 6, , 7, , -2, -3, -4, , 4), , Show the roots of the equation, diagram., Solution :, , x2 - 6x + 10 = 0 on the Argand, , 4, 3, 2, 1, -6, , -5, , -4, , -3, , -2, , -1 0, , 1, , -1, -2, -3, -4, , 51, , 2, , 3, , 4, , 5, , 6, , 7
Page 53 :
6) Find square roots of -7 + 24i., Solution :, , 53
Page 54 :
11. Sequence and series, (1) A sequence is generated by the formula Mn = an2 + bn + c, where, a, b and c are constants. If M1 = 4, M2 = 10 and M3 = 18, find, the values of a, b and c., Solution : In Mn = an2 + bn + c, we take n = 1, 2, 3 and evaluate, the expression. We get, �.a ��b � c � 4, �.a ��b � c � 10, �.a ��b � c � 18, , Solving these equations we get values of, calculations), , 6, , 2) Evaluate :, , (a), , �, , 2, 5, , (3) n, , a,� b,� c ., , (b) 729 � 243 � 81 � ............ � 3 � 1, , n �1, , (c), , �, , � 8(0.25), , n, , n�1, , 6, , Solution :, , (a), , �, n �1, , 2, 5, , (3) n �, , 6, , 2, 5, , � (3), , n, , � 52 [... � ... � ... � ..... � ..... � .....], , n �1, , = …………….., 54, , (write your
Page 55 :
= …………….., (b) 729 � 243 � 81 � ............ � 3 � 1, , (c), , �, , � 8(0.25), , n, , n�1, , 3), , If the ratio of H.M. and G.M. of two quantities is 12 : 13, then, show that the ratio of the numbers is 9 : 4., , Solution :, H .M . �, , Let numbers be a and b., 2ab, and G.� M � �, a�b, , The ratio of H.M. and G.M. of a and b is 12 : 13., ∴, ∴ …………………………………………………………………………, ∴ …………………………………………………………………………, ∴ …………………………………………………………………………, ∴ …………………………………………………………………………, ∴ …………………………………………………………………………, ∴ …………………………………………………………………………, ∴ …………………………………………………………………………, ∴ …………………………………………………………………………, 55
Page 56 :
∴ …………………………………………………………………………, ∴ …………………………………………………………………………, ∴ a : b = 9 : 4, , 4), , If a, b, c are in H.P., then show that, , Solution :, ∴ b�, , a, b, c, ,�, ,�, � are in H.P., b+c c+a a+b, , Given a, b, c are in H.P., ����.., ����., , ∴ b ����� ����, �, ∴ ab � bc � 2ac, , To show that, , ……., , (1), , a, b, c, ,�, ,�, � are in H.P., b+c c+a a+b, , i.e. to show that, , b+c c+a a+b, ,, ,�, a, b, c, c�a, , b�c, , are in A.P., a�b, , �, �, ��, i.e. to show that 2 �, ��, a, c, � b �, , R.H.A = ………………………….., , , = ………………………….., , , , = ………………………….., , , , = ………………………….., , , , = ………………………….., , , , = ………………………….., , 5), , The sum of three decreasing numbers in A.P. is 27. If -1, -1,3 are, added to them respectively, the resulting series is a G.P. Find the, numbers., Solution :, , 56
Page 57 :
6), , Find the sum of all three digit numbers which are not divisible by, 7., Solution :, , 57
Page 58 :
58
Page 59 :
12. Permutations and Combinations, (1) How many three-digit numbers can be formed using digits 0,2,3,5,6,8,9, if no digit is repeated in each of the following?, (a) there are no restrictions, , (b) number must be multiple of 5., , (c) numbers are greater than 600., (d) numbers are even and less than 400., Solution : To form a three digit number we have to perform three acts., To fill the hundreds place, to fill the tens place, to fill the units place., (a) As there is no restriction, hundreds place can be filled in 6 ways,, tens place in 6 ways and units place in 5 ways. (as repetition is, not allowed), The required number is 6 � 6 � 5 � 180, (b) Number must be multiple of 5., If the digit in the units place is 0 or 5 then the number will be, divisible by 5., We count numbers which ends with 5 and numbers which ends with, 0 separately., (i) To count three digit numbers formed using digits 0,2,3,5,6,8,9, which ends with 5 without repeating any digit., Digit 5 is used in units place and 0 can’t be used in hundreds place,, so hundreds place can be filled in 5 ways. Tens place in 5 ways., The number of three digit numbers that ends with 5 is 5 � 5 � 25, (ii) To count three digit numbers formed using digits 0,2,3,5,6,8,9, which ends with 0 without repeating any digit., Digit 0 is used in units place, so hundreds place can be filled in 6, ways. Tens place in 5 ways., The number of three digit numbers that ends with 0 is 6 � 5 � 30, ∴ The number of three digit numbers that ends with 5 or 0 is, 25 � 30 � 55, 59
Page 60 :
(c) Numbers are greater than 600. , , (d) Numbers are even and less than 400., , 2), , A shipment of 12 cell phones contains three defective units. In how, many ways can a buyer purchase four of these units and receive :, (a) all good units (b) two good units (c) at least two good units., , Solution :, , 60
Page 61 :
3), , In how many ways can we arrange 3 red flowers, 5 yellow flowers, and 7white flowers in a row? In how many arrangements no two, yellow flowers are adjacent to each other., (Flowers of the same color are identical)., , Solution :, , 61
Page 62 :
4), , There are 10 persons, among whom two are friends. Find the number, of ways in which they can be arranged around a circle. Also find, the number of arrangements in which :, (a) exactly one person is there between the two friends., (b) the two friends are always separated., , Solution : We know that n distinct objects can be arranged around a, circle in � n � 1�! Ways., , 62
Page 63 :
5), , Prove that (a), , n, , Pr �, , n!, (n � r )!, , (b) n Cr �, , Solution :, , 63, , n!, r!(n � r )!
Page 64 :
6), , A committee of 4 is chosen from 8 men and 6 women. Determine, the number of ways of selecting the committee if (a) there are no, restrictions (b) it must contain 2 men and 2 women (c) it must, contain only men (d) it must contain at least 3 men (e) it must, contain at least one of each gender., , Solution :, , 64
Page 65 :
13. Mathematical induction and Binomial theorem, (1) Prove the following statements using principle of Mathematical, Induction for all n ∈ N., a) n 2 + 3n is divisible by 2. b), , 1, 1, 1, 1, n, �, �, �, � ......... �, 1� 2 2 � 3 3 � 4, n � � n � 1� n � 1, , Solution : a) Let P � n � : n 2 + 3n is divisible by 2., To prove that P �1� is true., , �1�, , 2, , � 3 �1� � 1 � 3 � 4 , which is divisible by 2., , ∴ P �1� is true., , Now assume that P � k � is true for some � k ., i.e. assume that k 2 + 3k is divisible by 2., i.e. assume that k 2 � 3k � 2m for some integer m ., To prove that P � k � 1� is true., i.e. to prove that � k � 1� � 3 � k � 1� is divisible by 2., 2, , � k � 1�, , 2, , � 3 � k � 1� � k 2 � 2k � 1 � 3k � 3, , , , � k 2 � 5k � 4, , , , � k 2 � 3k � 2k � 4, , , , � 2m � 2k � 4, , , , � 2 � m � k � 2 � , where m + k + 2 is an integer., , ∴, , � k � 1�, , 2, , � 3 � k � 1� is divisible by 2., , ∴ P � k � 1� is true whenever P � k � is true., , By principle of mathematical induction, P � n � is true for all n ∈ N ., , b), , Let P � n � :, , n, 1, 1, 1, 1, �, �, �, � ......... �, 1� 2 2 � 3 3 � 4, n � � n � 1� n � 1, , 65
Page 66 :
2), , Using Binomial Theorem expand :, a), , � x � 3�, , 5, , b), , �, , x2 � 6, , �, , c) � 2 x � 3�, , 6, , 4, , Solution : We know that � a � b � � nC0 a n � nC1a n �1b � nC2 a n �2b 2 � ....... � nCnb n, n, , 66
Page 67 :
3), , Find the 5th term in the Binomial expansion of :, (a) � x � 3 y �, , Solution :, , 7, , (b) � 2 x � 7 �, , (c) � 2 x � 3 y �, , 4, , We know that � r � 1�, , 9, , th, , term in the expansion of � a � b �, , n, , is, , tr �1 � n Cr a n � r b r, , 4), , Find the coefficient A of the given term in each of the binomial, expansion :, 67
Page 68 :
We know that � r � 1�, , Solution :, , th, , term in the expansion of � a � b �, is tr �1 � n Cr a n �r b r, , n, , th, 6, a) Let the term in x be � r � 1� �, , term in � x � 5 �, tr �1 � Cr a, n, , n�r, , r, , b � Cr x, 7, , 7�r, , 5 is term in, r, , ∴ 7�r �6, ∴ r =1, ∴ r � 1 � 2 and 2nd term is in x 6, 7, =, C1 ( x)6 (5)1 35 x 6, , The coefficient of x 6 is A=35, b) � 3 y 2 � 1�, , 8, , c), , 4�, �, �x� �, x�, �, , c, , 7, , x6 ., , ∴ t2, =, , a, b, , 6, , 68, , d, , Binomial, (x + 5)7, (3y-2 - 1)8, 4�, �, �x� �, x�, �, , Term, A x6, A y-8, , 6, , (x + 2y)4, , A x0, A x2 y2
Page 69 :
d), , � x � 2y�, , 4, , 5), , Use Binomial theorem to express each of the following in the form, of a + ib :, (a) (1+ i)5 , (b) (3 − 4i)4 , (c) (2 − 7i)6, Solution :, , 69
Page 71 :
71
Page 72 :
14. Sets and Relations, (1) Use separate Venn Diagrams and shade the regions for the following:, (a) A , , (b) B', , (c) A ∪ B , , (e) A ∪ B' (f) A'∪ B' (g) (A ∪ B)', (i) A ∩ B (j) A'∩ B (k) A ∩ B ', (m) (A ∩ B)' , , (d) A'∪ B, (h) (A'∪ B)' , (l) A'∩B', , (n) (A ∪ B) ∪ (A'∪ B '), , Solution :, , 72
Page 73 :
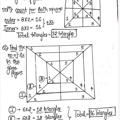
2), , Use separate Venn Diagrams and shade the regions for the following:, (a) A , (b) B', (c) A ∪ C , (d) B' ∪ C, (e) A ∪ B' ∪ C, (f) B' ∪ C' ∪ A (g) (A ∪ B) ∩ C', (h) (A'∪ B)' ∪ C , , (i) B ∩ A ∩ C (j) (C' ∩ B) ∪ A, , Solution :, , 3), , In a group of 50 students, 20 study subject A, 25 study subject B, and 20 study subject C. 10 study both A and B, 5 study both B and, C, 7 study both A and C. 2 study all three subjects., (a) show this information on Venn diagram, (b) find the number of students who study, (i) A only , (ii) B or C, (iii) A but not C , (iv) none of A , B or C., 73
Page 74 :
Solution :, , 4), , Show all possible relations from A = {a, b} to B = {5, 6} using, Arrow diagram. Find among them the relations that are :, (i) One-One relation, (ii) Onto relations, (iii) Null relation, (iv) Universal relation., , Solution :, , 74
Page 75 :
Let R be the relation defined by R = {(x, y) : x + 2y = 6, x ∈ W,, x ≤ 10, y ∈ Z}, Find (i) R , (ii) Domain of R, (iii) Co-domain of R, (iv) Range of R, Solution :, 5), , 6), , Given the relation R = {(2, 3), (3, 4)} on set S = {2, 3, 4}, add a, minimum number of ordered pairs so that the relation is (i) reflexive, (ii) symmetric (iii) transitive (iv) equivalence., Solution :, (i) reflexive : {(2, 3), (3, 4), (2, 2), (3, 3), (4, 4)}, (ii) symmetric : {(2, 3), (3,…) (3, 4), (4, …)}, (iii) transitive : {(2, 3), (3, 4), (…, ….)}, (iv) equivalence : {(2,3), (3, 4), ……………………………………….}, 75
Page 76 :
15. Functions, (1) Find the domain and the range of f � x � � 9 � x 2 ., Solution :, , If f : A → B and g : B → C are one-one functions then show that, g f : A → C � is also one-one., Solution :, 2), , 76
Page 77 :
3) Given log 2 = 0.3010 and log 3 = 0.4771 find the value of log 96 ., Solution :, , Theory : Vertical shift : For c > 0, f(x) + c shifts graph of f(x) to c, units upward, and f (x) - c shifts graph of f (x) to c units downward., Horizontal shift : For c > 0, f (x + c) shifts graph of f (x) to c units to, left, and f (x - c) shifts graph of f (x) to c units to right., Reflection about X -axis : - f (x) reflects the graph about X - axis, Reflection about Y -axis : f (-x) reflects the graph about Y - axis, Activity :, 1), , Draw the graph of f(x) = 2 x and h(x) = 2 x−4 on the same graph, paper., , 77
Page 78 :
2), , Draw the graph of f (x) = log x and h (x) = log (x + 1) on the, same graph paper., , 3), , Draw the graph of f (x) =, graph paper., , x and h (x) =, , 78, , x � 3 � 2 on the same
Page 79 :
16. Limits, (1) For a given ∈ > 0, find a δ > 0 such that whenever, |x - a| < δ ,, we must have | f(x) – l | < ∈, where f(x) = 4 x − 3 , l = 9 and a = 3 ., Solution :, , | f(x) – l | < ∈, , if and only if | 4 x − 3 – 9 | < ∈, if and only if | 4 x − 12 | < ∈, if and only if | x − 3 | <, Thus required � �, , , 4, , , 4, , For a given ∈ > 0, find a δ > 0 such that whenever, |x - a| < δ ,, we must have | f(x) – l| < ∈, where f(x) = 3x − 4 , l = 8 and a = 4 ., Solution :, 2), , f ( x) ., 3) If x 2 � 4 x � 5 � f � x � � 2 x 2 � 8 x � 9 for all x ∈ R, then find lim, x →2, Solution :, , 79
Page 80 :
4), , � 6 x � 3x � 2 x � 1 �, lim, Evaluate x�0 � x x x �, � 36 � 9 � 4 � 1 �, , Solution :, , 5), , � 2 � cos x � 3 sin x �, �, 2, x� �, �, 3, x, �, �, �, ��, �, 3, , Evaluate lim� �, , 80
Page 81 :
Solution :, , 6), , 3, �, � x � �2 �, �, � 2 � 1�, �, �, �, Evaluate lim� �, �, � x�, �, x�, � 2 � 2x � �, 2 � 3 2 � 1 � cos x � log, �, �, �, 2, �, �, �, ��, , Solution :, , 81, , �, �, �, �, ��, �, � ��
Page 82 :
82
Page 83 :
17. Continuity, (1) By, , drawing, , � x � 3,, f � x� � �, �2 x � 2,, , the, , graph, , for x � 1, for x � 1, , of, , f(x),, , test, , whether, , the, , function, , is continuous at x = 1 . Justify your answer., , Identify the type of discontinuity if it is discontinuous., Solution : Take points on the line y � x � 3 . Plot these points. Draw part, of the line for x < 1 . Take points on the line y � 2 x � 2 . Plot these, points. Draw part of the line for x ≥ 1 . The graph is continuous., There is no break, gap in this graph. From the graph we observe, that f � x � is continuous at x = 1, 10, , 8, , y = 2x + 2, , 6, , 4, , y = x + 3, , -6, , -4, , -2, , 2, , 0, , 2, , 4, , 6, , 8, , -2, , 2), , � x 2 � 3,, , Test the continuity of f � x � � �, � x � 4,, b) x = 2 c) x = 4, , for 0 � x � 2, for 2 � x � 4, , at a) x = 1, , Solution : a) To discuss the continuity of f � x � at x = 1 .We observe that, the definition of f � x � is uniform (same) in the neighbourhood of 1., lim f ( x) � lim( x 2 � 3) � �2, x �1, , x �1, , And f (1) � (1)2 � 3 � �2, 83
Page 84 :
∴ lim f ( x) � f (1), x �1, , ∴ f � x � is continuous at x = 1 ., , b) To discuss the continuity of f � x � at x = 2 We observe that the, definition of f � x � is not uniform (same) in the neighbourhood of 2., We have to evaluate the left and right limits separately., lim f ( x) � lim( x � 4) � �2 ∴ The right hand side limit is −2 ., x�2, , x � 2�, , lim f ( x) � lim( x 2 � 3) � 1 ∴ The left hand side limit is 1 ., x�2, , x � 2�, , lim f ( x) � lim� f ( x) i.e. the right hand side limit is not equal to the, , x � 2�, , x�2, , left hand side limit., ∴ Function f � x � is not continuous at x = 2 ., , c) To discuss the continuity of f � x � at x = 4 .We observe that the, definition of f � x � is uniform (same) in the neighbourhood of 4., , 3), , � x � 2, for � 2 � x � 0, Draw the graph of f � x � � ��0, forx � 0, �� x � 2, for 0 � x � 2, �, , Is f continuous at = 0 ?, Solution :, , 84
Page 85 :
� x2 ,, 4) Test the continuity of f � x � � �, � x, , for � 1 � x � 0, at x = 0 ., for 0 � x � 3, To discuss the continuity of f � x � at x = 0. We observe that, , Solution :, the definition of f � x � is not uniform (same) in the neighbourhood, of 0. We have to evaluate the left and right limits separately., , 85
Page 86 :
5) Draw the graph of function f � x � and discuss its continuity on its, domain., � x 2 � 1,, �, �� 2 x,, f � x � � � 1,, � 4 � 2 x,, �, �� 0,, , if � 1 � x � 0, if 0 � x � 1, if x � 1, if 1 � x � 2, if 2 � x � 4, , Solution :, , 86
Page 87 :
� x 2 � 1, for � 3 � x � 0, �, 6) If f � x � � � px � q, for 0 � x � 1 is continuous on its domain then find, � x � 1, for1 � x � 3, �, , values of p� and q ., Solution :, , 87
Page 88 :
18. Differentiation, (1) Test whether the function f(x) =, Solution :, , f(x) =, , x −1 is differentiable at x = 1., , x −1, , ∴ f �1� � 0 and f �1� h � � h, f (1 � h) � f (1), h, h �0, � lim, h �0, h, 1, � lim, , which does not exist., h �0, h, ∴ f � �1�� does not exist. ∴ f � x � is not differentiable at x = 1 ., f '(1) � lim, h �0, , 3, , 2) Test whether the function f(x) = � 2 x � 3� 2 is differentiable at, Solution :, , 88, , x=, , 3, ., 2
Page 89 :
3), , Show that the function f(x) is continuous but not differentiable at, x = 3, where, � x 2 � x � 3,, f � x� � � 2, � x � 3 x � 3,, , for x � 3, for x � 3, , Solution :, , 4), , Show that the function f(x) is continuous and differentiable at, �3 x 2 � 4 x � 3,, 2, � x � 12 x � 5,, , x = -2, where f � x � � �, Solution :, , 89, , for x � �2, for x � �2
Page 90 :
5) Let y = sin 2 x . Find, � dy �, � � ��., � dx � x �, , dy, using method of first principle. Hence find, dx, , 4, , Solution :, , 90
Page 91 :
6), , � x2 ,, �4 x � 2,, , Let f � x � � �, , for x � 2, for x � 2, , Evaluate the left derivative and right derivative of f � x � at x = 2 ., Is f � x � differentiable at = 2 ? Is f � x � continuous at = 2 ?, Solution :, , 91