Page 1 :
Chapter 2, , Units and Measurements, , Chapter Contents, , Introduction, , The International System of, Units, , Measurement of Length, Measurement of Mass, Measurement of Time, Accuracy, precision of, , instruments and errors in, measurement, , Significant figures, , Dimensions of Physical, Quantities, , Dimensional Formulae and, Dimensional Equations, , Dimensional Analysts and, Its Applications, , Some Important Definitions, Formulae Chart, Quick Recap, , Introduction, , Science is all about curious observations and the related careful, experiments. But we can appreciate a scientific observation more if, it can provide us precise and quantitative details., , For example, Newton observed an apple falling from the tree and this, led him to the discovery of gravitational force. But besides that he, also summarised his discovery in the form of a mathematical formula, which is known as Newton's law of gravitation. It made his, observation more relevant because it not only explained why an apple, falls to the ground but also tells about the force and the acceleration, with which it falls. Not only this, we can also find the force with, which moon is attracted towards earth, or earth is attracted towards, sun using this formula., , This illustration tells us the importance of quantitative description, and hence the need for measurement. This chapter deals with the, measurements of various physical quantities, their units and errors, in their measurements. We will also discuss significant figures in, measured values, and also how dimensional analysis help us to, understand the physical behaviour of a quantity., , Measurement is a process of determining how large or small a physical, quantity is as compared to a basic reference standard. This reference standard, is called the unit of the particular physical quantity. A unit can be chosen, arbitrarily but then it should be accepted internationally and should not vary, from place to place., , To express the measurement of a physical quantity, we need to know two, things:, w@ The unit in which the quantity is measured., , (ii) | The magnitude of the quantity i.e. the number of times that unit, is contained in the given physical quantity., , Aakash Educational Services Pvt. Ltd. Regd. Office : Aakash Tower, 8, Pusa Road, New Dethi-110005, Ph. 011-47623456

Page 2 :
32 Units and Measurements Board & Competitive Exams., , , , 4), , Measure of a physical quantity = Numerical Value ~ Size of unit, eg., Length of a rope = 10 m, , We deal with a number of physical quantities in physics, but the units of all these quantities can be, expressed in the units of few basic quantities. Thus physical quantities are of two types :Fundamental or Base Quantities : These are treated as independent of other physical quantities and, are not usually defined in terms of other physical quantities. The units for these quantities are called, fundamental or base units. There are seven base quantities. These are length, mass, time, electric, current, temperature, luminous intensity and amount of substance., , Derived Quantities : All physical quantities whose units can be expressed as combination of base, units are called derived physical quantities. Thus all quantities other than seven base quantities are, derived quantities e.g., velocity, acceleration, momentum, etc. Units of these quantities are called, derived units., , For example, speed of an object is given by the relation, , _ Distance travelled, Speed = “Time Taken, , . Unit of distance, Unit of speed = “(init of time, , or ms?, Other units can also be derived in a similar manner., , THE INTERNATIONAL SYSTEM OF UNITS, , , , A complete set of both the base units and derived units, is called the system of units. Historically many, systems of units were in use in different parts of the world. A few of them which were quite popular till recently, are given below., , 1., , 2., 3., , CGS System : In this system centimetre, gram and second are used as the base units for length, mass, and time respectively., , FPS System : It uses foot, pound and second as base units for length, mass and time respectively., , MKS System : It uses metre, kilogram and second as the respective units for length, mass and, time., , General conference on Weights and Measures developed and put forward a new system of units in the, , year 1971. This system, with units, their proper symbols and abbreviations was proposed to be used globally, in the field of science, trade and commerce. This system of units is now accepted internationally and is, called SI system. SI is an abbreviation for Systeme Internationale d’ unites (French name for, International System of Units)., , e The SI system is a decimal system, also known as metric system, a modernised and extended, form of metric systems like CGS and MKS., , @ There are seven base units and two supplementary units in SI. These units with their names and, symbols are given below., , Aakash Educational Services Pvt. Ltd. Regd. Office : Aakash Tower, 8, Pusa Road, New Delhi-110005, Ph. 011-47623456

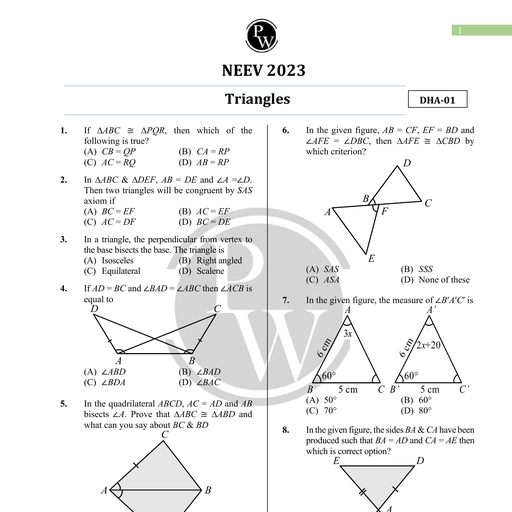
Page 3 :
Board & Competitive Exams. Units and Measurements 33, , , , , , , , , , , , , , , , , , , , , , Base Quantity Base Si | Unit Symbol, Unit, , Length metre m, , Mass kilogram kg, , Time second s, , Electric Current ampere, , Thermodynamic kelvin K, , Temperature, , Amount of substance mole mol, , Luminous intensity candela cd, , , , SUPPLEMENTARY UNITS, , , , Plane angle radian rad, , , , Solid angle steradian sr, , , , , , , , , , , , The base units used in SI system are defined as follows :, 1. Metre (m) : The metre is the length of the path travelled by light in vacuum during a time interval of, , 1, 299, 792, 458 of a second (1983)., 2. Kilogram (kg) : 1 kg is the mass of a cylinder made of platinum-iridium alloy kept at International Bureau, of Weights and Measures, at Severs near Paris, France. (1889), , 3. Second (s) : One second is the duration of 9,192,631,770 periods of the radiation corresponding to the, transition between two hyperfine levels of the ground state of the cesium-133 atom. (1967), , 4. Ampere (A) : One ampere is that constant current which when maintained in two straight, thin and parallel, conductors of infinite length, and placed 1 metre apart in vacuum, would produce between these conductors, a force of 2 x 10-7 newton per metre of length. (1948), , 1, 5. Kelvin (K) : One kelvin is the fraction 273.16 of the thermodynamic temperature of the triple point of water., (1967), The triple point of water is the temperature at which ice, water and water vapour co-exist., , 6. Mole (mol) : One mole is that amount of a substance which contains as many elementary entities as, there are atoms in 0.012 kilogram of carbon-12. (1971), , 7. Candela (cd) : One candela is the luminous intensity, in a given direction, of a source that emits, monochromatic radiation of frequency 540 x 10'? Hz and that has a radiant intensity in that direction of, , 1, 683 watt per steradian. (1979), , Aakash Educational Services Pvt. Ltd. Regd. Office : Aakash Tower, 8, Pusa Road, New Delhi-110005, Ph. 011-47623456

Page 4 :
34 Units and Measurements Board & Competitive Exams., , , , The remaining two SI units (Supplementary Units) and their respective quantities are defined as follows:, , (i) Plane Angle : The angle subtended by an arc of a circle at its centre is called a plane angle., Mathematically it is the ratio of the arc length ds of the circle to its radius r., , Thus plane angle do = s, , SI unit of plane angle is radian which is represented as rad., , One radian is defined as the plane angle subtended at the centre, of a circle by an arc equal in length to the radius of the circle., The total plane angle subtended by a circle at its centre is 2x radian., Another unit in which angle is measured, is degree., , , , 1°=_™ rad, 180, , One degree is also equal to 60 minutes and 1 minute is equal to 60 seconds, , 1° = —™_ rad = (60) = (3600)", , 180, (ii) Solid Angle : The angle subtended by a given surface area of a spherical surface, at its centre is called a solid angle. Mathematically it is the ratio of the intercepted, area dA of the spherical surface to the square of its radius r, as shown. d <a, , vr, , D, Thus solid angle dQ = a \W, SI unit of a solid angle is steradian and is represented as ‘sr.’ O, , One steradian is defined as the solid angle subtended at the centre of a sphere by a surface of, the sphere equal in area to that of a square, having each side equal to the radius of the sphere., , The SI units for all other physical quantities can be derived from the SI base units mentioned above., , Some physical quantities with their SI units in terms of the base units are given in the table in formulae, chart at the end of this chapter., , Some derived SI units are given special names. For example SI unit of force is kgms~?., It is also called "newton" in honour of the scientist Issac Newton. “newton” is denoted by the symbol, 'N'. Some other such units having special names are joule (J) for energy, watt (W) for power,, coulomb (C) for charge, volt (V) for potential difference, tesla (T) for the magnitic field strength etc. Some, derived SI units use these units with special names and the seven base units. For example SI unit, of work can also be written as “newton metre” or Nm. Similarly S! unit of power can be written as, "joule per second” or J s~'. A few more such units are : V m~" for electric field strength, C m for dipole, moment, N m~ for surface tension etc., , Did You Know?, , , , Guidelines for Writing SI Units in Symbols, , One should keep following points in mind while using symbols for S! units., , 1. Standard Unit Symbols are written in lower case roman type., , e.g. ‘metre’ has the symbol 'm’; ‘kilogram’ has the symbol ‘kg’, , 2. Unit names are never capitalised. However a unit symbol is capitalised only if the unit is named, after a scientist. e.g., units like 'newton'’, ‘joule’, ‘volt’, ‘ampere’ respectively have symbols as N, J,, VA., , 3. If a unit, named after a scientist, contains two letters in its symbol, then the initial letter of the, symbol is capital. For example, Hz for the unit 'hertz', Wb for the unit ‘weber and Pa for the, unit ‘pascal’., , Aakash Educational Services Pvt. Ltd. Regd. Office : Aakash Tower, 8, Pusa Road, New Delhi-110005, Ph. 011-47623456

Page 5 :
Board & Competitive Exams. Units and Measurements 35., , , , >, , , , 10., , 11., , Symbols are not followed by a fullstop., Unit symbols are never used in plural form. Thus a length of 100 metres is expressed as, 100 m and not as 100 ms., , Not more than one solidus (/) should be used in a unit symbol., For example, the SI unit of acceleration is written as m/s? and not as m/s/s., Pressure is expressed in the units of N/m? or N mr? but not as N/m/m., Thus writing 10 N/m? is correct., But 10 Nim/m is wrong., For inconveniently small or large values of quantities prefixes are used with their units to indicate, suitable multiples or submultiples, in powers of 10. For example, 10° m can be written as, kilometer or km, Tae m can be written as nanometer or nm. Here ‘kilo’ and ‘nano’ are prefixes, , to respectively indicate the amounts 1000 and iW, multiples and submultiples are given in table (1)., , Prefix symbol is written very close to the unit symbol without spacing between them. But if the, unit of a physical quantity is obtained by multiplying the units of two or more quantities, then, , these unit symbols are written with spacing between them., , Thus the symbol ms~ means per millisecond. But the symbol ms~' means metre per second., Thus ms~ and m s~ are two different physical quantities., , When a prefix is placed before a unit symbol, the combined prefix and symbol should be, considered as one new symbol which can be raised to a positive or negative power without any, bracket., , For example, km? means (102m)? and not 10°m*., , Similarly, 1s-! means (10-6 s)-' but not 10 s-1., , The use of double prefixes should be avoided as far as practicable., , Thus 10-'? m should be written as picometer or pm instead of writing as pum., , Unit names and unit symbols should not be used together while expressing a physical quantity., For example, unit of linear momentum should either be written as ‘kg m s~"' or kilogram metre, , per ‘second’ but not as ‘kg metre s~”., COMMON SI PREFIXES AND SYMBOLS FOR MULTIPLES AND SUB-MULTIPLES, , . Common SI prefixes and symbols for, , , , , , , , , , , , , , , , , , TABLE (1), Factor Prefix Symbol Factor Prefix Symbol, 10° Exa E 107° atto a, 10°° Peta P 107° femto f, 107 Tera T 10°? pico Pp, 10° Giga SG 10° nano n, 10° Mega M 10° micro n, 10° Kilo k 10° milli m, 107 Hecto h 107 centi c, 10° Deca da 10° deci d, , , , , , , , , , , , , , , , , , , , , , Aakash Educational Services Pvt. Ltd. Regd. Office : Aakash Tower, 8, Pusa Road, New Deihi-110005, Ph. 011-47623456