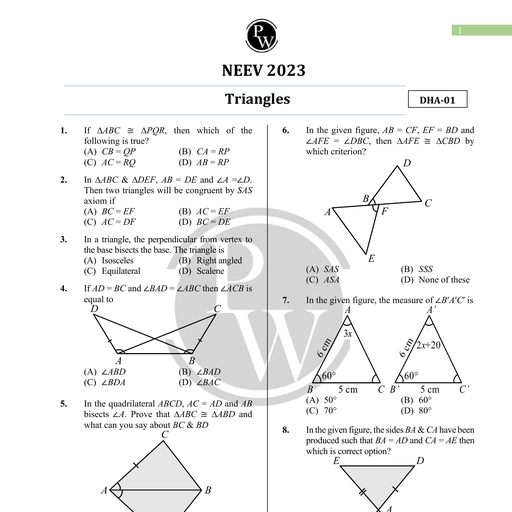
Page 1 :
Chapter 3, , Motion in a Straight Line, , e Introduction Introduction, , When we look around, we see a number of activities happening around, * Position. Path length and ys such as moving leaves of trees when the wind blows. vehicles moving, Displacement on roads, children playing etc. Even in our body we can see the examples, , of movements like the movement of air in and out of our lungs during, , © Average Velocity and Average reathing, beating of heart, flowing of blood etc. Our solar system, Speed belongs to the milky way galaxy in which all the planets including, earth are moving around the sun. Sun is also moving in the milky, , ¢ Instantaneous Velocity and way. The galaxy itself is not stationary, it is also moving in a group of, , Speed galaxies known as local group. In all these cases, there is something, common (Le., ‘movement’, but how can we say that the objects are, e Acceleration moving? They are moving as their position is changing with time, which, , is known as motion. So we can say that motion is that ‘something’, e Kinematic Equations for which is common in everything in the universe., Uniformly Accelerated Motion Now question arises. How does the position of object change with time?, While moving in a bus or a train when we look out, trees or buildings, © Relative Velocity appear to be moving backwards. What is the reason behind this, illusion? How can we compare the motion of two objects? To answer, ¢ Some Important Definitions these questions we have to study motion in detail., , © Formulae Chart ‘Kinematics’ is a branch of physics which deals with the study of, motion without considering the factors which causes motion. In this, © Quick Recap chapter we shall confine ourselves to the study of rectilinear motion, , Le., the motion of objects along a straight line and to simplify our, study, we will consider the object in motion as point objects. This is an, imaginary concept which is valid if the distances covered by the object, in a given duration of time is very large as compared to its size., , For example a car travelling hundreds of kilometre can be taken as a, point object., , In this chapter we will study, ¢ How to describe straight-line motion in terms of average velocity,, , instantaneous velocity, average acceleration, and instantaneous, acceleration., , ° Position-time, velocity-time and acceleration-time graphs for, straight line motion of objects., ° Equations of motion for uniformly accelerated motion, to solve, , problems involving straight line motion., , ° The concept of relative velocity, to compare the motion of two, objects., , Aakash Educational Services Pvt. Ltd. Regd. Office : Aakash Tower, 8, Pusa Road, New Delhi-110005, Ph. 011-47623456

Page 2 :
92 Motion in a Straight Line Board & Competitive Exams., , POSITION, PATH LENGTH AND DISPLACEMENT, , In previous classes, we have studied that if the position of an object is changing with time w.r-t. its surrounding,, then the object is said to be in motion. Otherwise it is at rest. So to describe the position of an object, we, need a reference point or a set of coordinate axes (x, y and z axis). As we are dealing with straight line, motion in this chapter, hence we need just one axis say x-axis so that it coincides with the path of object., Suppose you are observing a car and at time ¢t = O, the car is at point A and at t = 10 s,, t= 20s and t = 30s, car is at point B, C and D respectively. As its position is changing with time so the, car is in motion, and point A is the reference point for this observation. As you started observing its motion, when it was at point A., , A B Cc, t=0 t=10s t=20s, , , , , , 30s, Fig. : Motion of a car along a straight line (x-axis), , ‘Now, according to your observation the car is moving as you are the observer, but for a person sitting in the, car, the car is at rest all the time w.r.t. him and you are moving. So “motion” and “rest” are relative i.e., a, body at rest w.r.t. one person might be in motion w.r.t. some other person. This depends on the observer's, frame of reference. In the above example, you are observing the motion of car in a frame of reference attached, to you and the person sitting in the car is observing the motion of the car in a frame of reference attached, with himself. Thus the frame of reference is a system of coordinate axes attached to an observer having a, clock with him to record time, w.r.t. which he can describe the motion of a moving object., , Example 1: What is the state of a person sitting in a moving bus w.rt. a person standing at the bus stand and, wy?, , Solution : For the person standing at the bus stand, the person who is inside the moving bus is in motion, as the position of person inside the bus is changing with time w.r.t. him, , , , , , 1. What is required to specify the position of an object?, 2. Asays that B is in motion. But C says that B is at rest. Is this possible?, [Hint : Motion and rest are relative terms.], , , , , , Path Length, , Consider the motion of a boy along a straight line say x-axis and let the origin of x-axis be the reference point, i.e., the point from where the boy started moving. A, B and C represent the positions of the boy at different, instants of time. At tf = 0 the boy was at point A i.e., origin. Now lets consider the two cases of motion. In, the first case the boy moves from A to B and in the second case he moves back from B to C., , c A B, —40 °o +80 m, -x +x, Fig. : x-axis, origin and position of boy at different instants of time, , Aakash Educational Services Pvt. Ltd. Regd. Office : Aakash Tower, 8, Pusa Road, New Dethi-110005, Ph. 011-47623456

Page 3 :
Board & Competitive Exams. Motion in a Straight Line 93, , , , While moving from A to B, the distance covered by the boy is AB i.e., 80 m. In the second case the distance, moved by the boy is BA + AC i.e., (80 + 40)m = 120 m. You can see in figure that point C lies on the, negative side of x-axis, but while calculating the distance we are considering AC as (+ 40 m) instead of, (— 40 m) this is because the distance travelled by a body can never be negative. So in the second, case while going from A to C though, he is moving in the negative axis side, but the distance travelled by, him is positive. Distance is a scalar quantity as it has only magnitude and no direction. Now through out his, journey the boy moves first from A to B then back from B to C. So the total distance travelled by him is, (80 + 120) = 200 m. This is the path length. So we can define path length as the actual distance traversed, by an object during its motion in a given interval of time. Path length is also a scalar quantity as it has, only magnitude and no direction., , , , Displacement, The boy started his journey from A and finally reaches point C. The total distance traversed by him, during, his course of motion is 200 m. But what is the change in his position during his journey? The change in his, Position during his journey is from A to C i.e. 40 m towards negative x-axis., , This change in position is known as displacement which is a vector quantity. It has both magnitude, (40 m) and direction (towards negative x-axis). As we are dealing with motion along a straight line i.e., one, dimensional motion so, an object can have two directions i.e., forward and backward (for horizontal motion), and upward and downward (for vertical motion) and these directions can be specified by +ve and —ve signs., The change in a quantity is denoted by a Greek letter A(delta). Now let us discuss the displacement of boy, in detail. A and B are the i | and final positions of boy during his journey from A to B [fig. (a)]. Let these, Positions be x,(0 m) and x,(+ 80 m) at time ¢, and & respectively., , , , c A B, —40 °o +80 mM, (%, 6) +x (, 6), , Fig. (a) : Motion of boy from A to B, So change in his position in time At = (t, — t,) is Ax = x, — x, = 80 — 0 = + 80 m. The displacement has a, magnitude 80 and is directed in the positive x-direction as indicated by the +ve sign. In the second case he, moves back from B to A in time At = (t, — ,) and then from A to C in time At = (t, — t,). While coming back, from B to A [fig. (b)] his position changes from x, to x, in time Af = (t, — t,) and this change is given by, , Ax = x,- x, =0-80=-80m, , c A B, , -40 (x, 6) (4, 6), Fig. (b) : Motion of boy from B to A, , Here the displacement has magnitude 80 m and —ve sign indicates that it is directed towards the —ve x-axis., Now he moves from A to C fig. (c). Position of boy at C is x, so he is moving from x, to x, in time, At = (t, — t)., , Aakash Educational Services Pvt. Ltd. Regd. Office : Aakash Tower, 8, Pusa Road, New Deihi-110005, Ph. 011-47623456

Page 4 :
94 Motion in a Straight Line Board & Competitive Exams., , , , c A B, -40 fo} +80 mM, (%, &) (x. 6), x-axis, , Fig. (c) : Boy moving from A to C, , So the change in position is given by Ax = x, — x, = — 40 — 0 = — 40 m, the magnitude of displacement is, 40 m and —ve sign indicates that it is directed towards negative x-axis. The change in the position of boy, during whole journey can be calculated by adding these three displacements and we get, , Ax = + 80 m- 80 m-40m=—40m, So the displacement of boy at the end of his journey is -40 m, which has magnitude 40 m and directed, towards negative axis., Hence, we can define the displacement of an object in a given interval as the shortest distance between the, initial and final position of the object in a particular direction. The magnitude of displacement is always less, than or equals to the total distance i.e. the path length traversed by the body /.e.,, , |Displacement| < Distance, If an object is moving along a straight line without turning back then, the distance and displacement are equal., For example, when boy was going from A to B his displacement and path length were equal i.e., 80 m. But, after his journey, the total distance or the path length traversed by him is 200 m while his displacement, is -40 m. Similarly the displacement of an object can be zero but the distance or the path length traversed, by him can never be zero., , Note :, @ Distance is a scalar quantity while Displacement is a vector quantity both having same dimensions, (L) and SI unit [metre]., , (ii) The magnitude of Displacement is equal to straight distance between two positions; so, Distance = | Displacement |., , (iii) For motion between two points Displacement is single-valued while Distance depends on actual, path and so can have many values., , (i) For a moving particle Distance can never decrease with time while Displacement can., w For a moving particle Distance can never be negative or zero while Displacement can be., (w), , An object is said to be in uniform motion in a straight line if its displacement is equal in equal, interval of time, however smail the interval may be. Otherwise the motion is said to be non-uniform., , Example 2: A person walks along a semicircular path from A to B as shown in the figure given below., , , , Calculate the distance and displacement traversed by the person., , Solution : Distance travelled by the person from A to B is equal to the circumference of the semicircular, , path = xR., The shortest distance between the final position (8) and initial position (A) is AB = 2R, The displacement traversed by the person is 2R., , , , Aakash Educational Services Pvt. Ltd. Regd. Office : Aakash Tower, 8, Pusa Road, New Delhi-110005, Ph. 011-47623456

Page 5 :
Board & Competitive Exams. Motion in a Straight Line 95, , Try Yourself, , , , 3., , A particle travels along the path ABC, as shown in the figure given below, AB = BC = /,, calculate the path length and displacement of the particle, , B<—/—>C, i, A, [Hint : Use Pythagoras theorem to calculate the displacement.], , What is the ratio of displacement to the path length traversed by an object, if the object comes, back to its initial position?, , [Hint : When object comes back to its initial position its displacement is zero.], , , , , , =, Example 3 :, Solution :, , if the distance covered by a particle is zero, what will be its displacement?, , As the distance covered by the particle is zero. This implies that the particle is at rest or, stationary. Hence, its displacement is also zero., , , , , , Try Yourself, , , , A boy moves 400 m towards north, 300 m towards west and again 400 m towards south., Calculate the displacement of the boy from the initial position., , [Hint : Displacement of an object is the shortest distance between its initial and final position.], , Explain with the help of an example, if the displacement of a particle is zero, then it is not, necessary that the distance traversed by it is also zero., , [Hint : If object comes back to its initial position its displacement is zero.], , , , , , Example 4:, , Solution :, , Displacement of @ person moving from A to B alonga semicircular path of radius R is 100 m., What is the distance travelled by him?, , Displacement = 2R, , = 100=2R, , = R=50, , The distance travelled by the person is nR., So, the distance travelled by the person is 3.14 x 50 = 157 m, , , , , , , , , , , , Is displacement a scalar or a vector quantity?, , [Hint : Displacement has both magnitude and direction.), What is the S.1. unit of displacement?, , [Hint : It has the unit of length], , , , Aakash Educational Services Pvt. Ltd. Regd. Office : Aakash Tower, 8, Pusa Road, New Delhi-110005, Ph. 011-47623456