Page 1 :
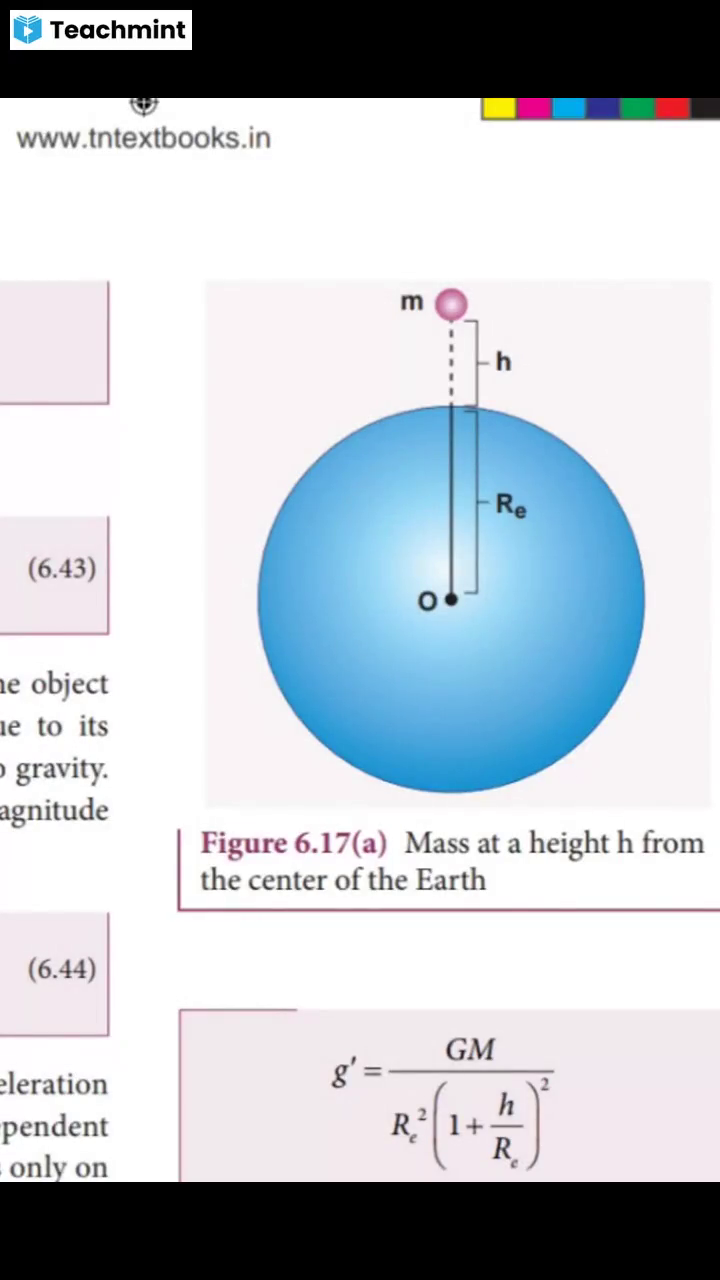
CO te NOW 6 €QUatnS =U aVNatOnal §=6froree —, || RL v2] |, , Newton's second law,, , @ UNIT 6 GRAVITATION, , | untrsxtPnysics vo-ainae 16 ® 7002020 1, , | ss 1 ® a |, , www.tntextbooks.in, , , , (6.43), , , , , , , , The acceleration experienced by the object, near the surface of the Earth due to its, gravity is called acceleration due to gravity., It is denoted by the symbol g. The magnitude, , of acceleration due to gravity is Figure 6.17(a) Mass at a height h from, the center of the Earth, , , , , , Isl=a*- (6.44), , experienced by any object is independent R?, , of its mass. The value of g depends only on, , the mass and radius of the Earth. Infact, ( ay, :, , It is to be noted that the acceleration g= ( h 2, 1+, , Galileo arrived at the same conclusion 400 g, years ago that all objects fall towards the, Earth with the same acceleration through, various quantitative experiments. The Ifh<R, acceleration due to gravity g is found to be t, 9.8 ms~ on the surface of the Earth near, the equator., , We can use Binomial expansion. Taking the, terms upto first order, , , , , GM h, Variation of g with g -H(1-22), altitude, depth and a :, latitude h, Consider an object of mass m at a height h g =«{1 24] Koes), , , , , , from the surface of the Earth. Acceleration, experienced by the object due to Earth is, , We find that g’<g. This means that as, , , GM altitude h increases the acceleration due to, , giz Rin (6.45). gravity g decreases., , Unit 6 GRAVITATION »), , | unreeot emacs veins 10 ® sron2000, , , , Le ® a TT, , www.tntextbooks.in, , , , The above two examples show that the, acceleration due to gravity is a constant, near the surface of the Earth., , , , 1. Calculate the value of g in the following, two cases:, (a) Ifa mango of mass % kg falls from, a tree from a height of 15 meters,, what is the acceleration due to, gravity when it begins to fall?, , Can we substitute h = R, in, , the equation 6.46? No. To get, equation 6.46 we assumed, that h<< R.. However h=R_