Page 1 :
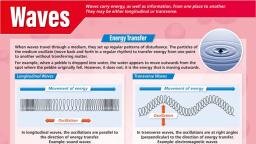
Chapter 15, , Waves, , ¢ Introduction Introduction, , Most of us experience the phenomenon of wave propagation when we, drop a stone in a pond of still water. These waves move outwards in, expanding circles until they reach the shore. It seems as if the water, © Displacement Relation fora is moving outward from the point of disturbance. If we examine, , © Transverse and Longitudinal, Waves, , Progressive Wave carefully the motion of a leaf floating on the disturbed water, we see, , that the leaf moves up and down about its original position but there, , e The Principle of is no displacement of leaf towards the shore. Thus we can say that, , Superposition of Waves energy is transferred but there is no transfer of medium. Such a, , pattern in which there is no actual transfer or flow of matter as a, , © Reflection of Waves whole but energy is transmitted from one part of a medium to another, e Beats part ts called wave., , Waves travelling in a medium are closely connected to harmonic, © Doppler Effect oscillations. This can be easily understood with the following, Some Important Definitions examples. Consider a group of springs connected to one another as, , shown in the figure below. If one end of a spring is pulled suddenly, ¢ Formulae Chart and released, the disturbance travels to its other end. Now the, Quick Recap second spring is also stretched or compressed since it is connected, , to the first spring. Similarly the third spring is compressed and so, on. Thus the disturbance moves from one end to the other end, but, each spring only executes simple harmonic motion about its mean, position., , ——ren000—wones—vo00s—E, , A group of springs connected to each other, , Similarly we can consider the propagation of sound waves in air. As, the wave propagates, it compresses or expands a small region of air., Density increases in the small region which is compressed and, hence the pressure in that region increases. Pressure is directly, proportional to the force. Therefore, there is a restoring force acting, in this region which is proportional to the disturbance as in the case, of a spring. If one region is compressed the particles of that region, are collected together. These particles then tend to move outward in, the adjoining region thus creating compression in the adjoining, , Aakash Educational Services Pvt. Ltd. Regd. Office : Aakash Tower, 8, Pusa Road, New Deihi-110005 Ph.011-47623456

Page 2 :
136 Waves Board & Competitive Exams., , , , region and rarefaction in the first region. In this way, the disturbance is propagated through the air, in the form of compressions and rarefactions., , In crystalline solids. group of atoms are arranged in a periodic lattice. These atoms resemble a group, of strings attached end to end. If one atom is displaced from its mean position, the disturbance travels, in the same manner as discussed in the case of group of springs connected end to end., , In this chapter, we will discuss the type of propagation of waves through different media, and the, factors affecting the speed of waves in them. We'll also discuss the superposition of waves and, Doppler's effect in sound., , ‘There are mainly three types of waves :, 1. Mechanical waves, 2. Electromagnetic waves, 3. Matter waves, , 1. Mechanical waves require a material medium for their propagation, They cannot travel through, vacuum. Sound waves, water waves, and waves on a spring etc. are some examples of mechanical, waves., , 2. Electromagnetic waves do not require a medium for their propagation. They can travel through, vacuum. X-rays, radio waves, light etc., are electromagnetic waves., , 3. Matter waves are associated with constituents of matter such as electrons, protons, neutrons,, atoms and molecules., , In this chapter, we will discuss mechanical waves and their characteristic properties in details., , TRANSVERSE AND LONGITUDINAL WAVES, , Mechanical waves are further divided into two parts :, 1. Transverse waves, 2. Longitudinal waves, , 1. Transverse waves : Transverse waves are the waves in which the constituents of the medium oscillate, perpendicular to the direction of wave propagation., , If we give an upward jerk to one end of a long rope that has its opposite end fixed, a single wave pulse, is formed and travels along the rope with a fixed speed., , , , a, , Pulse —», , , , But if we give continuous periodic up and down jerks to one end of the rope, a sinusoidal wave is, Produced on the rope. This disturbance moves from left to right as shown. But the particles of the string, oscillate up and down. We can say that the particles of the rope are oscillating about their mean position, in a direction normal to the direction of wave motion. Hence transverse wave is produced and propagated, in a rope., , , , Harmonic wave —>, , Aakash Educational Services Pvt. Ltd. Regd. Office : Aakash Tower, 8, Pusa Road, New Delhi-110005 Ph.011-47623456

Page 3 :
Board & Competitive Exams. Waves 137, , 2., , <a Knowledge Cloud, , Longitudinal waves : Longitudinal waves are the waves in which the constituents of the medium oscillate, along the direction of wave propagation. Consider a long air-filled pipe with a piston at its one end as, shown below. If we suddenly move the piston rightward and then leftward, we can generate a pulse of, compression and rarefaction along the pipe., , , , , , , , , , , , , , , , , , , , , , , , Rarefaction Compression, , If we push in and pull out the piston continuously and periodically, a sinusoidal wave is generated along the, pipe. As the motion of the elements of air is parallel to the direction of the wave's propagation in this case,, the motion is said to be longitudinal and the wave is said to be a longitudinal wave., , , , , , , , , , Solids have fixed shapes. Solids and strings (under tension) can sustain shearing stress. But fluids do not, have a fixed shape. Therefore, fluids do not sustain shearing stress. The propagation of a transverse, mechanical wave is such that it produces shearing stress in a medium. This is the reason that transverse, waves can be propagated through solids and strings but not in fluids. Solids, liquids and gases all can sustain, compressive strain. Therefore, longitudinal waves can be propagated through solids, liquids and gases., , , , Example 1: What kind of mechanical waves exist, , Solution : Inside water — Longitudinal waves, , , , (2) Inside water?, (b) On the surface of water?, , On the surface of water — Longitudinal as well as transverse waves, , , , Try Yourself, , 1. Explain why transverse waves cannot be propagated through fluids., 2. What is common in mechanical longitudinal and transverse waves., , , , , , , , DISPLACEMENT RELATION FOR A PROGRESSIVE WAVE, , , , If, during propagation of a wave in a medium, the particles of the medium perform simple harmonic motion then, the wave is called a ‘simple harmonic progressive wave’ and a plane progressive wave travelling in, +x direction is given by the equation :, , y=asin{ £-x)s¢ i), , while the equation of a plane progressive wave travelling in —x direction is given by, , y=asin {an( 4+) 9} ++ (ii), , Aakash Educational Services Pvt. Ltd. Regd. Office : Aakash Tower, 8, Pusa Road, New Deihi-110005 Ph.011-47623456

Page 4 :
138 Waves Board & Competitive Exams., , These equations may also by written, respectively as, 2:, y=asin {28 ot-x0} «il), 2n, and y=asin {220t+x0} «ivy, , Note 1 : In the above equations, ‘v' represents the speed of the wave and not that of the particle. The particle, speed is given by, , dy _,an t x r, a. - 2Fcos{2n( £ = *) tol corresponding to equation (i), or Ye 2 er cos 2n( t+ xs +>} corresponding to equation (ii)., at : nT a x, Note 2: equation of a travelling wave can be written in several forms such as, , y~asin{ an (£3) +0 =asin{(wt+ kx) +o} =asin{ k(t =x) +9} ~asin{o(ts*)+o}, , 2:, Here w= > [T is time period] is called angular frequency, , 2.2, [Ais wavelength and v is wave velocity]., This 'k' is called “angular wave number” or propagation constant., , As we told earlier if a room has a lot of pendulums and the air blows in it then the displacement (y) of any, pendulum from its mean position is not only dependent on the position (x) of the pendulum hanging point in, the room but also depends on time (f)., , It has been shown analytically that any function of space and time which satisfies the equation, oy = at ay ...(A) represents a wave., , ox? v? ot?, , Here y is the wave function and doesn't necessarily denote y co-ordinate., , y =Asinot or y = A sinkx don't satisfy the above equation so do not represent waves, while functions, , y =A sin(wt — kx), y = Alog(at + bx), , y =Asinkx sinwt = or y = Asin(@t — kx) + Bcos(wt + kx), , Satisfy the above equation, so represent waves., , Equations of the form y = F(at + bx) represent travelling or progressive waves. Following are the common, travelling wave equations :, , k=, , Travelling, y = Alog(at + bx), y= /(ax+ bt), y = (ax — bt)’,, y= Ae o- 4", y = Asin(ax — bt)?, y = acos*(int — kx) or, , y = acosAwt sin(wt — kx), , But y = A sin(2x? — 3), y = A sin(ax® + bt), y = coskx. sinwt don't represent traveling or progressive waves., They may be called waves if they satisfy equation (A)., , If a traveling wave is a sine or cosine function it is known as harmonic wave., , Aakash Educational Services Pvt. Ltd. Regd. Office : Aakash Tower, 8, Pusa Road, New Deihi-110005 Ph.011-47623456

Page 5 :
Board & Competitive Exams. Waves 139, , , , In our exam we are asked just to recognize the equations of spherical and cylindrical progressive waves., , A, y= A sin(wt — kr) represents spherical progressive waves while y = ap aati) represents cylindrical, , Progressive waves., , Maximum exam questions are related to one dimensional plane progressive waves which is given by, y = Asin(wt ¥ kx + >), , Very straight forward, only formula based questions will be asked at this stage so without going deep into the, , mathematics of wave equation, just remember the meaning of each term and the various forms in which the, equation can be written as follows :, , (a) y in general is disturbance produced by the wave but right now remember its just the displacement of, medium particles (pendulum in the room in which air blows) from its mean position. It'll be given in, centimeter or meter., , (b) Arepresents the amplitude or maximum displacement of the medium particle from the mean position,, will be given in centimeter or metre., , (c) w is known as angular or circular frequency of medium particle in oscillation under SHM. Its unit will, , be radian per sec. w = 2nv = 22 where vis natural frequency given in hertz or per sec or cycle per sec., , T is time period given in second., (d)_ tis the variable time from when the wave begins. Given in second., (e) -ve sign between ¢ and x indicates that the wave is travelling in +ve x direction., , () kis called propagation constant or wave number and given by k = aE, where A is the wavelength., , Note that i is also written as v or wave number which indicates the number of waves per metre., , (g) xis the position of the mean position of the medium particle from where the wave has started., , (h) The constant ¢ is called phase constant or initial phase. It is used to find the position from where time, is considered. Henceforth we shall take o = 0 unless otherwise stated., , There is unitary relation between time period T, phase angle 2x and path difference i. So if two medium particles, , are separated by a distance x, the phase difference between them will be at or time lag/lead between them, Tx, it as, will be a, , When a wave changes medium its frequency doesn't change but wavelength changes and phase velocity, MY AY, , chi . So, PD =:, vore anges. vy AQ, , Wave or phase velocity c = distance/time = a- av =<, , Medium particle velocity v, = & = wAcos (wt ¥ kx), , So, maximum particle velocity v,,,.. = WA, Sometimes in the exam, ratio of maximum particle velocity and wave velocity is demanded which is, , (Particle velocity v, at a given position and time is equal to negative of the product of wave velocity with slope, of the wave form at that point)., , Aakash Educational Services Pvt. Ltd. Regd. Office : Aakash Tower, 8, Pusa Road, New Deihi-110005 Ph.011-47623456