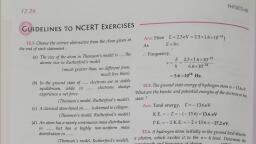Page 1 :
4ron®, orbital frequency of electron in nth orbit is 121, » v 1A ; (by Axqyr?, ve" nr mr op mr An ne?, 2 mk 2)? . (66.10), nh 4n° mk @? auk, 3 AP KO 6 10", 4nom | re “9x10 x91 10 x(Lo«1o 8 ™, 2 te "5.2610 U yy, 4n” mk~ ¢, : wh 0.53 «10° yy or05saA, , The, he length is of the order of atomic alee (, , same as obtained in equation (1), 0" m),, , is 12.15. TH, wich » of ; oe total energy of an electe, Hence for large value of n, the classical trequeney of State of the hydrogen atom ‘ about car ene, ution of electron in nth orbit is same as that obtained (4) What is the k, pohr's theory. ake te Mnetic energy of the electron in this, Classically, an electron can be in an whit y, yp.14. Clas ‘om, Then ler Vv around (b) What is the potential energy of the electron in this, ie nucleus of an atom. Then what determines the typical state ?, , jc size ? Why is an atom not, say, thousand times bigger (, iis ti ypical size ? The question had Sreatly puxzled Bohr, he arrived at his famous model of the atom that you have, , arti the text. To simulate what he might well have done, , Which of the answers, , above would change if the, choice of the, , Zero of potential energy is changed ?, ICBSE Diec], Ans, K.B. of an electron in nth orbit,, , his discovery, let us play as follows with the basic 2, ants of nature and see if we can get a quantity with the Ts | S, ions of length that is roughly equal to the known size oy i, a (- 10°) f PB, of an electron in nth orbit,, () Construct a quantity with the dimensions of length from Ve kZe* =~2T, be fundamental constants e, m, and c. Determine its numerical f, on Total energy,, (b) You will find that the length obtained in (a) is many E=T+V=T-2Ta-T, , orders of magnitude smaller than the atomic dimensions,, further, it involves c. But energies of atoms are mostly in, non-relativistic domain where c is not expected to play any role, Ta~ Ew~(-3.4)=3.40V,, This is what may have suggested Bohr to discard ¢ and look for (b) Potential energy,, , ‘something else’ to get the right atomic size. Now, the Planck’s, constant h had already made its appearance elsewhere. Bohr’s, great insight lay in recognising that h, m,, and e will yield the (©) If the zero of the potential energy is chosen, right atomic size. Construct a quantity with the dimension of “ifferently, kinetic energy does not change. Potential, length from h, m,, and e and confirm that its numerical value Metgy and hence total energy will be affected., , has indeed the correct order of magnitude., , (a) Kinetic energy,, , V =-2T=-2x34=- 6.6 eV., , 12.16. If Bohr’s quantisation postulate (angular momentum, , eke? e = nh/2n) is a basic law of nature, it should be equally valid for, , Ans. (a) The quantity is ie the case of planetary motion also, Why then do we never speak of, ee quantisation of orbits of planets around the sun ?, , which has the dimension of length. Ans. Angular momenta associated with planetary, , 2 2 motion are incomparably large relative to h/2n. Por, , le] = ML P'Q'M (LT? a aT = L example, angular momentum of the earth in its orbital, , Anzymc? ML'TOM.(T ) motion is of the order to 10” /2n. In terms of the, , Also Bohr’s quantisation postulate, this corresponds to a, , : very large value of n(of the order of 10”), For such large, , e 9x10? x(1.6 x10")? values of n, the differences in the successive energies, , 4neyme2 9.1 10! x(3 x 10°) and angular momenta of the quantised levels of the, a ; Cae Bohr model are so small compared to the energies and, , This | pis x1 angular momenta respectively of the levels that one, i | purposes, consider the levels —, i ical atomic can, for all practica, , sie (= iri) much smaller than the typic Pa