Page 2 :
Superposition of waves, What are progressive waves?, Waves which continuously travel in a given, direction are called progressive waves., When progressive waves travel through a, medium the particles of the medium perform, vibrations about their mean positions., If these vibrations are simple harmonic, vibrations, the waves are called simple, harmonic progressive waves., Both transverse as well as longitudinal waves, are simple harmonic progressive waves., The waves reach different particles of the, medium at different time instants., Hence there is a phase difference between the, vibrations of different particles of the medium., Therefore, in simple harmonic progressive wave, s behind its previous particle in, phase, even though all particles vibrate with the, same amplitude, period and frequency., Q.6) State the characteristics of simple harmonic, progressive waves., Characteristics of S. H. P. waves :, 1) The S.H.P. waves continuously advance in the, same direction through a given medium., When these waves travel through a medium, the, particles of the medium perform simple, harmonic motion of the same amplitude, same, period and the same frequency., The phase of the vibrations is different for, different particles of the medium., Each particle lags behind the previous particle, 5) The distance between two particles, which differ, radians, is called the wavelength, 6) S.H.P. wave is doubley periodic., 7) These waves, are classified into two groups:, i) Transverse waves and ii) Longitudinal waves, State any four characteristics of simple, monic progressive waves., Q.7) Define the terms amplitude, wavelength,, period and .frequency of a wave., , The magnitude of maximum displacement of a, particle of the medium from its mean position is, called the amplitude of the wave., [a] = [M0L1T0], (Page1), , Superposition of waves
Page 3 :
2), , Wavelength ( ) :, The distance between two successive particles of, the medium which are always in the same state of, vibration or oscillation (having phase difference, 2π rad) is called the wavelength of the wave., S. I. unit : m, Dimensions : [λ] = [M0L1T0], Period (T) :, The time taken by the particles of the medium to,, complete one oscillation is called the period of the, wave., S. I. unit : second (s), Dimensions : [T] = [M0L0T1], Frequency (n) :, The number of oscillations of the particle of the, medium per unit time is called the frequency of, the wave., The frequency is equal to the reciprocal of the, period., , 3), , 4), , S. I. unit : hertz (Hz), Dimensions : [n] = [M°L0T–1], 5) Velocity :, The distance covered by the wave per unit time is, called velocity of the wave or wave velocity., S. I. unit : m/s, Dimensions : [v] = [M0L1T–1], Q.8) Obtain the relation between velocity, wave, length and frequency of a wave., Ans., Relation between wave -velocity, frequency, and wavelength :, We know,, , In one period (T), a wave covers a distance equal, to one wavelength ( )., But, , = n = frequency, , Wave velocity = frequency wavelength, Q.9) Wave is doubly periodic motion explain, Ans :, 1) When waves are propagated through a medium, it, is found that at any point of the medium, the form, of the wave repeats after equal intervals of time., Thus, a wave motion is periodic in time., 2) It is also found that at any instant, the form of the, wave goes on repeating at equal distances. Thus, a, wave motion is periodic in space., 3) This consideration shows that a wave motion has, doubley periodicity i.e., it is periodic in time and, periodic in space., 12th (Sci.), , Example :, If we consider a leaf on a water surface. The, leaf keeps on oscillating on the water surface at, regular time intervals showing that it is periodic, in time. If we observe another leaf at same, distance it also oscillates in a similar manner. So, we can see that many crests are formed at the, same distance showing periodicity in space., Q.10) Derive an expression for a one dimensional, simple harmonic progressive wave travelling, in the direction of the positive X-axis., Express it in different forms., Ans., Expression for a one dimensional S.H.P., wave travelling in the +X-axis :, 1) Consider a simple harmonic progressive wave, travelling along the X-axis in the positive, direction as shown in figure., , 2), , In figure,, y = represents displacement of each particle and, x = represents position of the particle i.e.,, distance from origin., 3) Suppose that at t = 0, the particle at the origin is, at its mean position O. Then at any instant of, time t, the displacement of the particle is given, by, y = a sin t, ..... (i), where, a = amplitude of S.H.M. and,, = angular velocity of S.H.M., 4) Now consider a particle of the medium, situated, at the point P at distance x from origin O. The, disturbance at O will reach the particle at F only, after some time. Hence particle at P lags behind, the particle at O in phase., 5) Let be the phase difference between particle P, and particle at origin O. Then the displacement, of the particle at P at the instant t will be given, by, y = a sin ( t – ), ..... (ii), 6) A distance X is equivalent to the phase, difference 2π rad. Hence the distance x is, equivalent to a phase difference of 2 x/λ, , (Page2), , δ=, , .......(iii), Superposition of waves
Page 4 :
Substituting the value of, , in equation (ii), we get, , If T is the period of wave,, , This is the equation of a simple harmonic, progressive wave travelling in the positive, direction Of the X-axis., Different forms:, from eqn . (iv), 1, T, , = frequency of the wave, ......(v), , But v = n = the velocity of the wave, , .......(vi), , 4), , A rubber tube is connected to the funnel and a, listener can hear the ticking of the clock by, keeping the ear close to the free end of the, rubber tube., 5) Observations :, i) On moving the funnel away from and towards, S2, along the common axis, it is found that the, ticking sound is heard clearly when the funnel is, at F2., ii) The loudness of sound is less at other points on, the axis., 6. Conclusions :, i) Sound waves starting from the watch at F1 get, reflected from S1. The reflected waves travel, parallel to the axis and fall on S2 which focuses, (converges) them at F2., This shows that sound waves reflect from large, curved surface,, ii) Reflection of sound waves from a curved, surface occurs in the same way as that of light, waves., Q.12) Define wave velocity and particle velocity, Ans., 1) Wave velocity :, The velocity of propagation of wave is called, wave velocity, 2) Particle velocity :, The velocity with which particles of the medium, oscillate during propagation of wave is called, particle velocity., Q.13) Explain the reflection of transverse waves, from a denser medium and rarer medium., Ans., Reflection of transverse waves from a, a) Denser medium, 1) Consider a single crest of transverse waves, travelling along a string and incident normally, on the surface of a denser medium., , Q.11) Explain the reflection of transverse and, longitudinal waves from a curved surface., Ans., Reflection of transverse and longitudinal waves, from a curved surface :, 1) Consider two large concave reflecting surfaces S1, and S2 having foci F1 and F2 respectively., 2) Arrange these reflecting surfaces co-axially and, facing each other., 3) Place a source of sound, e.g., a clock at F1 and, place a funnel on the common axis facing S2 as, shown in fig., , Fie Reflection of transverse wave from, denser medium, 2), , 12th (Sci.), , (Page3), , When crest incident of wave velocity (vw) is, towards the surface of denser medium and, direction of particle velocity (vp) is in the, upward direction., Superposition of waves
Page 5 :
3), 4), , 5), i), ii), , 6), , b), 1), , The particles of the denser medium are not free, to vibrate., As the crest reaches the fixed particle, it exerts, upward force on the particle. By Newton's III, law of motion, the particle exerts an equal and, opposite downward force on the string (crest)., Due to this,, Wave velocity (vw) is reversed and wave travels, in the opposite direction and, Particle velocity (vp) is also reversed and there, is a change of phase rad or 180°., Thus a crest is reflected as a trough., Similarly, we can explain that trough is reflected, as crest from denser medium., Hence when transverse wave is incident on the, surface of denser medium crest is reflected as, through and vice versa (trough as a crest)., Rarer medium., Consider a single crest of transverse waves, travelling along a string and incident normally, on the surface of a rarer medium as shown in the, following figure., , 1), , 2), , 3), 4), , 5), , 3), , The particle of the rarer medium are free to, vibrate., 4), As the crest reaches the particle, it exerts, upward force on the particle. But the particle of, the medium will not exert the force of reaction, on the crest, so it will vibrate in the same, direction of the crest (upward)., 5), Due to this,, i), Wave velocity (vw) is reversed so wave travels, in the opposite direction and, ii), The direction of particle velocity is in the same, direction of the crest., Therefore the direction of particle velocity does, not change so there is no change in phase. Thus,, crest reflects as crest., 6), Similarly we can explain that trough reflects as, trough from rarer medium. Hence, when, transverse wave is incident on the surface of, rarer medium, crest is reflected s crest and, trough is reflected ns trough., Q.14) Explain the reflection of longitudinal (sound), waves from a surface of a, a) denser medium, b) rarer medium., Ans. a) Denser medium :, 12th (Sci.), , 7), 8), , b), 1), , 2), , (Page4), , Consider a single compression of longitudinal or, sound waves is incident on the surface of denser, medium., When compression is incident, both the, direction of wave velocity and particle velocity, (vp) are directed towards the surface of denser, medium., , The particles of the denser medium are not free, to vibrate., As the compression incidents on the fixed, particles it exerts force in the forward direction., By Newton's III law laws of motion, particles, exert an equal and opposite (backward) force on, the compression., Due to this, both wave velocity and particle, velocity are reversed, i.e., directed away from, the surface of denser medium. However the, displacement of the particles in the reflected, wave is opposite to that displacement in the, incident wave so that there is a change of phase, rad or 180°., Thus, compression is reflected as compression., Similarly, we can explain that rarefaction is, reflected as rarefaction., Hence, when longitudinal wave is incident on the, surface of denser medium compression is, reflected as compression and rarefaction is, reflected as rarefaction., Rarer medium :, Consider a single compression of longitudinal or, sound waves is incident on the surface of denser, medium., When compression is incident, both the, direction of wave velocity and particle velocity, (vpre directed towards the surface of denser, medium), , Superposition of waves
Page 6 :
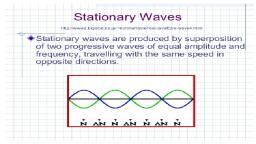
3), , The particles of the rarer medium, are free to, vibrate., 4), As the compression incidents on the particles of, the medium, it exerts a force towards the surface, (forward), particles do not exert force of, reaction on the compression so it will vibrate in, the same direction of the compression., 5), Due to this,, i), Wave velocity (vw) is reversed and wave travels, in the opposite direction,, ii), The direction of particle velocity is in the same, direction of the compression. Therefore, the, direction of particle velocity does not change so, there is no change in phase (phase change is, zero). Thus, compression reflects as rarefaction., 6), Similarly, we can explain that rarefaction is, reflected as compression., 7), Hence, when longitudinal wave is incident on, the surface of rarer medium, compression is, reflected as rarefaction and rarefaction is,, reflected as compression., Q.15) State and explain the principle of super, position of waves., Ans., Principle of superposition of waves :, When two or more waves travelling through a, medium arrive at a point of the medium, simultaneously, each wave v produces its own, displacement at that point independently of the, others. .Hence, the resultant displacement at, that point is equal to the vector sum of the, displacements due to all the waves., Explanation :, 1), When two different-waves cross a particle of a, medium simultaneously. Each wave behaves as, if the other wave is not present and would set, the particle into two SHM's due to the two, waves., 2), Hence the resultant displacement of the particle, at any instant would be equal to the sum of the, displacement due to both the waves. This is, called principle of superposition of waves., 3), Let, y1 and y 2 be the displacements due to, waves acting separately., y = resultant displacement due to two waves by,, the principle, of superposition of waves, i) If two waves are in phase,, 4), , ii) If two waves are out of phase,, ., Interference of sound waves :, The phenomenon of, enhancement, or, cancellation of displacement produced due to, the superposition of sound waves, is called, interference of sound waves., , 12th (Sci.), , The principle of superposition is true in case of, longitudinal as well as transverse waves., Types of interference :, a) Constructive interference :, When two sound waves arriving at a point, simultaneously are in phase i.e., compression of, one wave coincides with compression of other, or rarefaction of one wave coincides with, rarefaction of other. Then the resultant intensity, of sound is maximum at that point. This effect is, called constructive interference., b) Destructive interference :, When the two sound waves arriving at a point, are out of phase i.e., compression of one wave, coincides with rarefaction of other or, rarefaction of one wave coincides with, compression of other Then the resultant, intensity is minimum at that point. This effect is, called destructive interference., Example :, Beat is an example of interference of sound, waves, Q.16) What is a stationary wave? Why is it, called stationary ?, Ans., Stationary wave :, When two identical progressive waves (having, same amplitude, period, wavelength and speed), travelling in the same bounded medium, along a, same straight line but in opposite directions, by, their superposition, they produce a resultant, wave in the form of loops which does not travel, in any direction. This resultant wave is called, stationary wave or standing wave., Stationary waves :, 1) Stationary wave is produced by superposition of, two identical waves travelling in opposite, direction., 2) As the velocities of two waves are equal in, magnitude and opposite in direction the, resultant velocity of the wave is zero., 3) Due to this, the resultant wave does not transfer, energy through the medium or remain localised, and cannot be propagated through the medium., Hence the resultant wave is called stationary, wave or standing wave., Q.17) Explain the formation of stationary wave., Ans., 1) When progressive waves travelling through a, medium are incident normally on a rigid, boundary they are reflected with a phase change, of rad., 2) The reflected waves have the same amplitude, and wave length as the incident wave but they, travel in opposite direction., , (Page5), , Superposition of waves
Page 7 :
3) Due to the superposition of these two identical, progressive waves traveling in opposite, directions, resultant wave is formed in the, medium., This resultant wave does not travel in any, direction called stationary wave., Therefore the resultant stationary wave is formed, in the medium., Q.18) State and define the different types of, stationary waves., Ans :, 1) Stationary waves are produced due to the, superposition of two simple harmonic, progressive waves., 2) Both transverse as well as longitudinal waves are, simple harmonic progressive waves., 3) Considering this fact stationary waves are, classified into two groups., a) Transverse stationary waves, b) Longitudinal stationary waves, a) Transverse stationary wave :, A stationary wave formed due to the, superposition of two identical transverse, progressive waves travelling with same spied tut, in opposite directions is called transverse, stationary wave., Examples :, The stationary waves produced in the vibrating, ii) Sonometer, iii) Melde's experiment, b) Longitudinal stationary wave :, A stationary wave formed due to the, superposition of two identical longitudinal, progressive waves travelling with same speed, tut in opposite directions is called longitudinal, stationary wave., Examples :, The stationary waves produced in the vibrating, air columns of, i) Open organ pipe, ii) Closed organ pipe, iii) Resonance tube experiment, , 2) A simple harmonic progressive wave travelling, along the positive direction of X-axis is, represented by, , 3) A simple harmonic progressive wave travelling, along die negative direction of X-axis is, represented, , 4) By the principle of superposition of waves, the, resultant displacement at that point is given by, y = y1 + y2, , We know the formula, , Using the formula, we can write, , cos 2, , Q.19) Explain analytically the formation of, stationary waves. Why is it called so? Show, that nodes and antinodes are equally spaced, in a stationary wave., Ans., Analytical treatment of stationary waves ., 1), , Consider two identical progressive waves ot, amplitude a, period T, wavelength, , traveling, , in the same finite medium along the same path, , But, , but in opposite direction., 12th (Sci.), , (Page6), , Superposition of waves
Page 8 :
Therefore at these points nodes are produced., Distance between any two successive nodes is, nodes is., , Where,, , = amplitude of the resultant wave., 5) Equation (i) shows that the resultant stationary, wave is also a simple harmonic progressive wave., Whose period (T) is same as that of two waves., 6) Stationary wave :, In the equation (i) the term, , 9) Antinodes and conditions for antinodes:, Antinodes :, When stationary waves are set up in a medium,, there an some points at which displacement is, always maximum are called antinodes., So antinodes are the positions of maximum, amplitudes. ., Conditions :, The amplitude is maximum at antinodes., At antinodes,, , is absent., , The absence of this term shows that the resultant, wave is not travelling in forward or backward, direction i.e., not a progressive wave. Hence the, resultant wave is a stationary wave., 7) Amplitude of stationary wave :, The amplitude of stationary wave is, , Thus, in case of stationary wave, the amplitude of, oscillation is not same for all the particles., It varies (changes) harmonically with the position, (x) of the particle., 8) Nodes and conditions for nodes :, Nodes :, When stationary waves are set up in a medium,, there are some points at which displacement is, always zero are called nodes., So nodes are the positions of zero amplitudes., Conditions: The amplitude (displacement) at nodes, is zero., At nodes,, A = 0 ( mini, value of cos θ = 0), , Substituting P = 0, 1, 2,...., we get, , So at these points antinodes are produced., , 2, 10) Conclusions :, , i) From equation (iii) and (v), distance between any, two successive nodes and antinodes is, , ., , This shows that nodes and antinodes are equally, speed., ii) From (iv) and (ii),, first antinode is formed at x = 0 and, first node is formed at x =, , ., 4, Therefore the distance between adjacent nodes, and antinodes, This shows that nodes and antinodes are, alternately produced., Q.19) State the characteristics of stationary waves., 12th (Sci.), , (Page7), , Superposition of waves
Page 9 :
Ans :, , 15) The length of each loop is, , Characteristics of stationary waves :, , ., , 16) All the particles in one loop (between two, successive nodes) vibrate in the same phase as, shown in fig. (b)., , Fig. Stationary waves, 1) Stationary waves are produced due to the, superposition of two exactly identical simple, harmonic progressive waves travelling through, same medium but in opposite directions., 2) The resultant velocity of stationary wave is zero., Therefore these waves cannot be propagated, through the medium. In other words, they do not, transfer energy through the medium., 3) The disturbance is confined to a particular region, between the starting point and reflecting point of, the wave., 4) In stationary waves,-the amplitude of oscillation is, not same for all the particles. It varies, harmonically with the position (x) of the particle. It, varies from zero (at nodes) to maximum (at, antinodes)., 5) In stationary waves, there are some points at which, amplitude of displacement is zero, are called, nodes., 6) In stationary waves, there are some points at which, amplitude is maximum, are called antinodes., 7) The distance between any two successive nodes or, antinodes is, , where λ = wavelength of the wave., , 8) The distance between node and adjacent antinode, 9) The antinodes and nodes are alternately produced., 10) Antinodes and nodes are equally spaced., 11) All particles of the medium except at the nodes,, perform S.H.M. of the same period as that of, component waves but of different amplitude., 12) Nodes are the points of the medium which are, permanently at rest Therefore the velocity at the, nodes is zero., 13) Antinodes are the points of the medium which, vibrate with maximum displacement. Therefore, velocity at antinodes is maximum., 14) Loops are formed between every two successive, nodes as shown in fig. (a)., , 12th (Sci.), , 17) The particles in adjacent loops (on the two sides, of .nodes) are in out of phase or opposite phase,, (differ in phase by n rad.) as shown in fig. (b)., 18) All the particles of the medium (except at nodes), cross their mean position simultaneously, twice, in each period or oscillation., 19) The wavelength, frequency and period of, stationary wave is same as that of each of the, component waves., 20) The energy density is twice that of in the, progressive waves (incident and reflected wave).., 21) Stationary waves can be produced by the, superposition of transverse waves as well as, longitudinal waves., 22) In longitudinal stationary waves, pressure, changes are maximum at displacement nodes., Hence displacement nodes are pressure, antinodes., 23) In longitudinal stationary waves, pressure, changes are zero at displacement antinodes., Hence displacement antinodes are pressure, nodes., 24) Stationary waves are periodic in space and, periodic in time, (i.e., possess doubly, periodicity)., Stress and strain is maximum at nodes., Stress and strain is minimum at antinodes., In stationary waves, all the particles (except at, nodes) possess maximum K.E. while passing, through the mean position., 25) In stationary waves, all the particles (except at, nodes) possess maximum RE. at extreme, position of vibration., 26) The distribution of KE. and RE. changes with, time., 27) Examples of stationary waves :, i), If string is fixed at both ends and vibrated,, transverse stationary waves are produced with, nodes at the fixed ends,, ii) In resonance tube experiment, longitudinal, stationary waves are produced with a node at the, fixed end and an antinode at the free end., , (Page8), , Superposition of waves
Page 10 :
Q.20) What are pressure nodes and pressure, antinodes?, Ans., 1. Pressure nodes :, i), In longitudinal stationary wave (sound wave),, there are some points at which amplitude, (magnitude of displacement) is maximum, are, called antinodes or displacement antinodes., ii) But at these points pressure variation is, minimum, therefore these points are called, pressure nodes. Hence displacement antinodes, are pressure nodes., 2. Pressure antinodes :, i), In longitudinal stationary wave (sound wave),, there are some points at which displacement is, minimum, are called nodes or displacement, nodes,, ii) But at these points pressure variation is, maximum therefore these points are called, pressure antinodes. Hence displacement nodes, are pressure antinodes., Q.21) What is harmonic and overtone ?, Ans. Harmonics :, The frequencies which are integral multiples of, the fundamental frequency are called harmonics., The word harmonics is used to indicate the, fundamental frequency and all its integral, multiples, irrespective of whether they are, actually present m the given sound or not., The minimum (smallest) frequency is, fundamental frequency. It is also called the first, harmonic., If the fundamental frequency or first harmonic is, n then,, 2n is called second harmonic,, 3n is called third harmonic and so on., Thus, harmonic represents all integral multiples, of fundamental frequency., b.Overtones :, 1) The integral multiple of fundamental frequencies, excluding (other than) fundamental frequency, which are actually produced by the instrument are, called as ., 2) Frequency which are actually produced by the, instrument are called overtones. (actually present), 3) The word overtone is used to indicate only those, multiples of the fundamental frequency which, are actually present in the given sound., 4) The first frequency greater than the fundamental, frequency is called first overtone, the next higher, frequency is called second overtone and so on, Overtones are always present in sound note., 5) Example :, Inside a closed organ pipe, air column can vibrate, only with fundamental frequency and its odd, multiples., 12th (Sci.), , 6) If n is the fundamental frequency, the air column, can vibrate with the frequencies n, 3n, 5n, ...., Thus in this case, fundamental frequency (first, harmonic) = n first overtone (third harmonic) =, 3n second overtone (fifth harmonic) = 5n and so, on., 7) In complicated system like drum, circular, vibrating disc, overtone need not be integral, multiples of fundamental frequency., Q.22) State the formula for velocity of a, transverse wave along a stretched string and, obtain an expression for fundamental, frequency of the vibrating string., Ans., 1) If the stretched string is plucked at any point then, transverse progressive waves travel along the, string., 2) The velocity of a transverse wave along a, stretched string is given by, v, , ......(i), , m, Where, T = tension in the string, m = mass per unit length or, linear density of the string., 3) Consider a string of length £ stretched between, two rigid supports., 4) If the string is plucked and then released, a, transverse wave propagates along its length and, is reflected at the end., 5) Due to the interference between incident and, reflected waves, transverse stationary waves are, formed on the string., Nodes (N) are formed at rigid ends and antinodes, (A) are formed in between them as shown in, figure, , Let, l = length of the string, = wavelength of the wave, 6) We know that,, , 2, , ...... ii, , 7) The frequency of vibration (n) is given by,, , (Page9), , Superposition of waves
Page 11 :
Let, M = Mass of the string, L = Length of the string, A = Area of the string, v = Volume of the string, ρ = Density of the material of the string, r = Radius of cross section of the string, , v, , n, n, , .........from i, , n, , 2, , .........from ii, , Now,, , This is an expression for fundamental frequency of, a vibrating string. This is the lowest (smallest), frequency of a string. It is also called threshold, frequency., Q.23) State and explain laws of vibrating string, Ans., 1) Laws of vibrating string :, The fundamental frequency of vibrations of a, string is given by, , Putting the value of m in equation (i) we get,, , n, Where, = length of the string, T = tension in the string m = mass per unit length, or linear density of the string., 2) Law of length :, The fundamental frequency of transverse, vibration of a stretched string is inversely, proportional to its vibrating length if the tension, in the string and linear density of the string are, kept constant., i.e., n, , n, , [If T and mare constant], , n = constant, n1 1 = n2 2, 3) Law of tension :, The fundamental frequency of transverse, vibration of a stretched string is directly, proportional to the square root of the tension in, the string if linear density and vibrating length of, the string are kept constant., i.e. n $ √, [If and m are constant], &, = constant, √', Q.24)Show that the fundamental frequency of, vibrations of a stretched string is inversely, proportional to, i) the radius of the string and, ii) the square root of the density of the, material of the string., Ans., The fundamental frequency of vibrations of the, stretched wire is given by,, 12th (Sci.), , But, A = r2, , r, , Thus, the fundamental frequency of vibration is, inversely proportional to,, i), , radius of the string,, , ii), , The square root of the density of the material, of the string., , Q25) Explain the modes of vibration of a, stretched string., Ans :, The string can vibrate in different ways with, different frequencies. The different ways in, which string can---are called modes of the, vibration of the string., Consider a string of length stretched between, two rigid supports., , (Page10), , Superposition of waves
Page 12 :
If the string is plucked and then released, a, transverse wave propagates along its length and, is reflected at the end., Due to the interference between incident and, reflected waves, transverse stationary waves are, formed on the string, as shown in the figure., , Fig.(a)Fundamental mode of vibration of string, , Fig. (b) Second mode of vibration of string, , Fig. (c) Third mode of vibration of string, In figure, N = Node, A=Antinode, Fig. Modes of vibration of string, Boundary condition :, Nodes (N) are formed at rigid ends and antinodes, (A) are formed in between them. '5., We know, loop is formed between two successive, nodes., Therefore, length of one loop is the distance, between two successive node., , Putting the value of λ from equation (iii) in, above equation, we get, , I. First mode or fundamental mode or first, harmonic :, • The mode of vibration of a stretched string in, which string vibrates with only one loop (P=1)is, called fundamental -mode or first harmonic., In this mode, two node are formed at fixed ends, and antinode at the centre., This mode is shown in the figure (a)., The frequency (n) of fundamental mode is, by, putting P = 1 in equation (v)., , This is lowest (smallest) frequency of vibration, of string so it is called fundamental frequency or, first harmonic., II. Second mode or first overtone or second, harmonics :, The mode of vibration of a stretched string in, which string vibrates with two loops (P=2) is, called first overtone or second harmonic., In this mode, three nodes and two antinodes are, formed., This mode is shown in the figure (b)., , Therefore, length of one loop is the distance, between two successive nodes., , The frequency of first overtone (n,) of this mode, is given by putting P = 2 in equation (v)., , ......(i), , length of one loop =, Let, P = number of loops, Length of P loops = P, , n1, , .....(ii), , 2, length of string = length of P loops, P, , frequency, so it is called first overtone. Thus,, , from (i) and (ii), , frequency of first overtone (n1) is twice the, fundamental, , frequency, , (first, , harmonic)., , Therefore it is called second harmonic., , The velocity- of transverse wave is given by, .......(iv), , Where m = mass per unit length or linear, density of the string, We know, v = λ, , 12th (Sci.), , ..... vii, , It is the first frequency higher than fundamental, , .....(iii), , v, , 2n, , II. Third mode or second overtone or third, harmonics :, The mode of vibration of a stretched string in, which string vibrates with three loops (P=3)is, called second water or third harmonic., In this mode, four nodes and three antinodes are, formed., This mode is shown in the figure (c)., , (Page11), , Superposition of waves
Page 13 :
The frequency of second overtone (n2) of this, mode is given by putting P = 3 in equation (v)., , n2 = 3n, It is the second frequency higher than, fundamental frequency, so it is called second, overtone. Thus, frequency of second overtone, (n2) is the fundamental frequency (first, harmonic) ., Therefore it is called third harmonic., IV. Pth mode or (P–1)th overtone or Pth, harmonic:, Similarly, we can say, i) The Pth overtone = (P + 1)th harmonic, nP = (P + 1)n, where nP = frequency of Pth overtone, n = fundamental frequency, ii) From equation (vi), (vii) and (viii),, Modes of vibrations of the string gives, frequency n, 2n, 3n, ...., iii) Thus, even as well as odd (All) harmonics are, present as overtone in modes of vibration of, string., General formulae :, i) Frequency of Pth harmonic (nP) is, nP, P), , nP, , is, , T, , Q.26) Write a short note on sonometer., Ans: A sonometer consists of a uniform wire, stretched over a rectangular sounding box, and, passes over, , two movable bridges (or knife edges) and a, pulley. It works on the phenomenon of, resonance. The tension in the wire is adjusted by, adding weights to the hanger attached to the free, end of the wire. The length of the wire between, the movable bridges, L, is adjusted to vibrate in, unison with a given tuning fork either by beats, method or by Paper-rider method. L is called the, 12th (Sci.), , vibrating length. First, the vibrating length is set, to minimum and then gradually increased in, small steps. In the beats method, the wire and, the tuning fork are simultaneously set into, vibrations for each vibrating length Beats can be, heard when the two frequencies are very close., Then, a finer adjustment of the wire is needed so, that no beats are heard. This is when the ...two, are in unison., For the paper-rider method, a small light, paper in the form of A is placed on the wire at, its centre. The stem of the vibrating tuning fork, is gently pressed on the sonometer box. The, vibrating length is gradually increased from, minimum till the paper' rider vibrates and, thrown off. Because, when the wire resonates, with the tuning fork at its lowest fundamental, mode, the wire vibrates with maximum, amplitude and the centre of the wire is an, antinode. Hence, the paper rider is thrown off., A sonometer is used to determine the, frequency of a tuning fork and to verify the laws, of vibrating strings., Q.27. Explain the use of a sonometer to verify (i) the law of length (ii) the law of tension, (iii) the law of linear density., Ans., (i) Verification of law of length : According to this, 1, law, n $ ), if T and m are constant. To verify, this law, the sonometer wire of given linear, density m is kept under constant tension T. The, length of the wire is adjusted for the wire to, vibrate in unison with tuning forks of different, frequencies n1, n2, n3, .... . Let L1, L2, L3, ... be, the corresponding resonating lengths of the, wire. It is found that, within experimental errors,, n1L1= n2L2 = n3L3 =...... . This implies that the, product, uct, nL = constant, which vertifies the, law of length., (ii) Verification of law of tension : According to, this law, n $√T, if L and m are constant. To, verify this law, the vibrating length L of the, sonometer wire of given linear density m is kept, constant., A set of tuning forks of different frequencies is, used. The tension in the wire is adjusted for the, wire to vibrate in unison with tuning forks of, different be the frequencies n1, n2, n3, ...., T1,, T2, T3, .....be the corresponding tensions. It is, found that, within This experimental errors, n1 n 2, n3, n1, . This implies, =, T T2 T3, T, constant which verifies the law of tension., , (Page12), , Superposition of waves
Page 14 :
(iii) Verification of linear density : According to this, law n, , , if T and L are constant. To verify, m, this law, two wires having different linear, densities m1 and m2 are kept under constant, tension T., A tuning fork of frequency n is used. The, lengths of the wires are adjusted for the wires to, vibrate in unison with the tuning fork. Let L1 and, L2 be the corresponding resonating lengths of the, wires. It is found that, within experimental errors,, L2 m 2 . This implies L m =constant. According, , to the law of length of a vibrating string, n, , ., , which verifies the law of linear density., m, Examples :, i) The resonance tube experiment, the vibrations of, air column inside the tube, when vibrating fork is, held Over it, are forced vibrations., ii) Vibrations of clock pendulum, (amplitude is, constant)., iii) Vibrations of the string of the sonometer, experiment before the paper rider is thrown out. ., iv) When soldier are marching on a suspension, bridge, the bridge performs forced vibrations., Q.28) Explain the phenomenon of resonance., Ans : Resonance :, The phenomenon in which the body vibrates under, the action of an external periodic force, whose, frequency is equal to the natural frequency of the, body, so that the amplitude of vibrations becomes, very large is called resonance., 1. Resonance is a special case of forced vibrations., 2. The amplitude of forced vibrations depend upon, difference between the frequency of external, periodic force and natural frequency of vibration, of body., 3. If this difference is small then amplitude of, vibrations become large and vice versa., 4. When the difference between frequency of, applied force and natural frequency of body, becomes zero (i.e. frequency of external periodic, force and natural frequency of vibration of body, are equal) the amplitude of vibrations become, very large. Then the body is said to be in, resonance with driving force and the driven, vibrating body., 5. Thus, if the difference is large then the amplitude, of forced vibrations is small. If this difference is, changed, the amplitude of forced vibration goes, on decreasing on either sides of resonance as, shown in fig., 12th (Sci.), , Fig. Resonance curve, Amplitude vs frequency curve is called, resonance curve., 7. The frequency at which resonance occurs is, called the resonant frequency., Q.29) Give the examples of resonance., Ans., Examples of resonance:, 1. If two identical pendulums are suspended side by, side from a horizontal flexible support (rubber, or string) as shown in figure., When pendulum A is set into oscillation and it, is called driver, the horizontal supports responds, this oscillation. It is observed that B also starts, vibrating with its amplitude increasing to, maximum as shown figure(The phase difference, of π/2 is between oscillation of A and B)., 6., , Fig. Resonance of two pendulums, Response is inversely proportional to its relative, length, the best response (i.e., resonance) is, observed at equal lengths of pendulum., Electrical resonance is provided by tuning of, radio receiver. At given instant several, broadcasting, stations, are, emitting, electromagnetic waves of different frequencies., All these are simultaneously intercepted by the, aerial / antenna connected to the radio receiver., By timing the dial marked 'tuning' the frequency, of oscillatory circuit in the receiver is made, equal to the frequency of wave broadcast by the, desired station. Thus only the signals of that, frequency are amplified by the receiver and, signal of other frequencies are rejected. The, resonant vibrations of stretched string and their, laws of vibrations can be studied by using, i) Sonometer and ii. Melde's experiment, ii) Sonometer experiment demonstrates the, formation of stationary wave, resonance and to, determine unknown frequency of fork., , (Page13), , Superposition of waves
Page 15 :
where N =frequency of the fork, n = frequency of, vibrating string and m = linear density of string., iii) Melde's experiment also demonstrates the, formation of stationary wave in the form of, number of loops., a. Vibrations of prong of tuning fork are parallel to, the direction of propagation of the wave, then in, Meldes' experiment, the frequency of the tuning, fork (N) a double the frequency of vibration of the, string (n)., , Q.30) State the applications of resonance., Ans., Applications of resonance :, 1. By using principle of resonance, unknown, frequency of vibrating tuning fork can be, calculated., 2. Radio receiver can be tuned to a desired, frequency by using principle of resonance., 3. In resonance tube experiment, the resonating, length of air column is measured and the velocity, of sound in air at room temperature is calculated., 4. A hollow wooden box is provided for the stringed, musical instruments (examples : Violin, guitar,, sitar, and sarangi) when the string vibrates, the air, inside the box vibrates with same frequency., Resonance occurs and a louder, pleasant sound is, produced., 5. To increase the intensity of sound in musical, instrument, 6. To analyse musical note., 7. It is used in LCR circuit to match the impedance., Q.31) Explain why soldiers are ordered to break, steps when crossing a bridge., Ans., 1. The regular and systematic stepping of the, soldiers exerts a periodic force on the, suspension bridge. Therefore, the bridge begins, to vibrate., 2. If the frequency of the periodic force is equal to, the natural frequency of vibrations of the bridge,, resonance may occur., 3. Due to this resonance, the bridge may vibrate, with maximum amplitude and may even, collapse., 4. In order to avoid this danger, the soldiers are, ordered to break up their steps when crossing a, suspension bridge., , 12th (Sci.), , Q.32) In a sonometer, how is the frequency of the, vibrating wire affected when the attached, load is completely immersed in water ?, Ans., 1. We know frequency of the wire is directly, proportional to the square root of the tension., i.e.,, ., 2. On immersing the load in water, the apparent, weight of the load and hence the tension in the, wire decreases. Due to decrease in tension the, frequency of the vibrating wire also decreases., Q.33) A sonometer wire stretched by a load of, density , has a fundamental frequency n1., When the load is completely immersed in, water of density ,w, its fundamental, frequency is n2., Show that, Where S = relative density or specific, gravity., Ans :, Let,, T1 = W1 = weight of the load in air, T2 = W2 = weight of the load in water., Relative density or specific gravity (s) :, It is the ratio of weight of body in air to the, loss of weight of body in water., , S, , From equation, , (Page14), , ST1 – ST2 = T1, ST1 –T1 = ST2, (S–1)T1 = ST2, , Superposition of waves
Page 16 :
Q.34) Explain the vibrations of air column in closed, organ pipe., Ans. Closed organ pipe :, A long closed organ pipe is a cylindrical tube, having an air column with one end closed., 1. A vibrating tuning fork is held horizontally near, the open end of the closed pipe., 2. Sound waves are sent by source (vibrating tuning, fork) near the open end., 3. Suppose a compression (C) is produced, this, travel through air column and get reflected from, the rigid boundary as compression because there, is least freedom for motion of particle., 4. The reflected compression reaching the open end,, gets reflected as rarefaction because there is, maximum freedom for motion particle., 5. Suppose a rarefaction (R) is produced by the, prong of tuning fork and it travels through air, column and get reflected from rigid boundary as, rarefaction., 6. The amplitude of vibration of air column inside ., , i., , ii., , 5., , The air particles at the closed end is not free to, vibrate. Therefore a node is formed at the closed, end., The air at the open end of the pipe is, comparatively more free to vibrate. Therefore, an antinode is formed at the open end., Therefore, there must be a node at the closed, end and an antinode at the open end., Let, = length of vibrating column, X = wavelength of the wave, The air column inside a closed organ pipe can, vibrate with different modes as shown in figure., , become maximum i.e., stationary wave is formed, (it occurs due to resonance)., 7., , The necessary conditions is that the time taken to, produce a compression and rarefaction is equal to, time taken by the wave to travel twice the length, of tube., , 6., 7., , Where, v = velocity of sound in air at given, temperature., , Fig. Modes of vibration of air column pipe, closed at one end., The velocity of sound in air is given by ‘V’ = n, First mode or fundamental mode or first, harmonic:, The mode of vibration of an air column inside, a closed organ pipe, in which one node at, closed end and one antinode at open end is, formed is called fundamental mode or first, harmonic., This mode is shown in fig. (a)., , v, , The frequency (n) of vibration at resonance is, , The fundamental frequency (n) of air column is, given by putting the value of λ in equation (i), , v, , n, , Q.35) Show that only odd harmonics are, present as overtone In the case of an air, column vibrating In a pipe closed at one end,, Ans., Modes of vibration of air column in Pipe, closed at one end :, 1. Consider a closed organ pipe (pipe closed at one, end) containing air column., 2. If waves are sent along the air column in a pipe, closed at one end, they get reflected at the, closed end., 3. Due to the interference between the incident, waves and the reflected waves, longitudinal, stationary waves are formed in the air column., 4. Boundary conditions :, 12th (Sci.), , .....(i), , 8., , (Page15), , Second mode or first overtone or third, harmonic:, The mode of vibration of air column inside a, closed organ pipe, in which two nodes and two, antinodes are formed is called first overtone or, third harmonic., This mode is shown fig. (b)., , The frequency of first overtone (n1) of air, column is given by putting the value of λ1 in, equation (i), Superposition of waves
Page 17 :
3., , n1, , 9., , nf = 3n, ......(ii), It is the first frequency higher than fundamental, frequency, so it is called first overtone (n1) is, thrice the frequency fundamental frequency (first, harmonic).Therefore its is called third harmonic., Third mode or second overtone harmonic:, ., The mode of vibration of air column inside a, closed organ pipe, in which three antinodes are, formed is called second overtone or fifth, harmonic., , The frequency of second overtone (n2) of air column, is given by putting the value of λ2 in equation (i), , n2, It is the 2nd frequency higher than fundamental, frequency, so it is called second overtone. Thus,, frequency of second overtone (n2) is five times, the fundamental frequency (first harmonic}., Therefore it is called fifth harmonic., Conclusions :, From eqn. (i), (ii) and (Hi) we can conclude that,, In a closed organ pipe, air column vibrates with, frequencies n, 3n, 5n,...., i) Therefore, only odd harmonics are present as a, overtone in case of an air column vibrating in a, pipe closed at one end (i.e., n, 3n, 5n etc)., ii) Even harmonics are absent as a overtone in case, of an air column vibrating a pipe closed at one, end., iii. In genera), for Pth overtone, , 4., , 5., , 6., , v = nλ. Therefore frequency (n), n =, Q.37) Show that even as well as odd (all), harmonics are present as overtone in the case, of an air column vibrating in a pipe open at, both ends., Ans., Modes of vibrations of air column in a open, organ pipe :, 1. Consider a open organ pipe (open at both the, ends) containing air column., 2. If waves are sent along the air column in a pipe, open at both ends, they get reflected at the open, end., 3. Due to the interference between the incident, waves and the reflected waves, longitudinal, stationary waves are formed in the air column., 4. Boundary conditions :, There must be an antinode at both open ends., The air particles at the open ends are free to, vibrate and therefore there must be antinodes at, both open ends., 5., , Let, = length of an organ pipe, λ = wavelength of the wave, The air column inside an open organ pipe can, , nP = (2P + 1) n, where n = fundamental frequency, In closed pipe n : n1: n2 : ...... = 1 : 3 : 5 : ....., Q.36) Explain vibrations of air column in a pipe, open at both ends?, Ans., Open organ pipe :, An open organ pipe is a cylindrical tube, containing an air column open at both ends., 1. A source of sound (tuning fork) near one end, sends the waves in the pipe., 2. Suppose a compression (C) produced by the, tuning fork, travels downward through the air, column and get reflected as rarefaction 'R' at the, open end because there is maximum freedom, for motion of air column., 12th (Sci.), , The rarefaction moves upwards and get, reflected as compression at another open end., If at this moment the tuning fork also produced, compression. The vibrations of the air column, will be maximum and resonance occurs., It suffers second reflection at the open end near, the source and then interference with the near, wave coming in by a path difference 2 ., At resonance if n is the frequency of vibration, of wave then velocity of sound wave is given by, , (Page16), , vibrate with different modes as shown in figure., , Fig. Modes of vibration of air column pipe, open at both ends, Superposition of waves
Page 18 :
6., , The velocity of sound is given by, , 7., , First mode or fundamental mode or first, harmonic :, The mode of vibration of air column inside an, open organ pipe in which two antinodes at both, the open ends and one node inside the pipe is, formed is called fundamental mode of vibration., This mode is .shown in fig (a), , λ, , 2, , Frequency of second overtone (n2) is given by, putting the value of λ2, , n2, n2 = 3n, ...(iv), It is the second frequency higher than, fundamental frequency, so, it is called second, overtone., Thus frequency of second overtone (n2) is thrice, to fundamental frequency (third harmonic)., Therefore it is called third harmonic., Q.38) What is end correction? How is it, , The fundamental frequency (n) of air column is, given by putting the value of λ in equation (i), , n, , estimated? Is the end correction for a pipe, open at both ends the same as that for a pipe, , .......(ii), , closed at one end? Why?, , This is the lowest frequency with which air, column can vibrate inside an open organ pipe., , Ans :, Longitudinal stationary waves are formed in an, , This frequency is called fundamental frequency or, , air column inside a organ pipe(pipe closed at one, , first harmonic., 8., , Second mode(first overtone or second, harmonic), The mode of vibration of air column inside an, open organ pipe in which three antinodes and, two nodes are formed is called first overtone or, second harmonic., This mode is shown in fig (b)., The length of air column is given by,, λ1, Frequency of first overtone (n,) is given by, putting. the value of A, in equation (i), n1 =, , ., , n1, n1 = 2n, , 9., , .......(iii), It is the first frequency higher than fundamental, frequency, so it is called first overtone., Thus, frequency of first overtone (n1) is twice the, fundamental, frequency, (first, harmonic)., Therefore it is called second harmonic., Third mode or second overtone or third, harmonic, The mode of vibration of air column inside an, open organ pipe in which four antinodes and, three nodes are formed is called second overtone, or third harmonic., This mode is shown in fig (c), , 12th (Sci.), , end and pipe open at both ends), 1. End correction :, The antinode is not formed exactly at the open, end but a little distance beyond it. The distance, between open end of organ pipe and antinode is, called end correction., 2. Estimation :, The end correction e is calculated by the formula, e = 0.3 d, where d = inner diameter of pipe., 3. end correction is not same for a pipe closed at, one end and a pipe open at both ends., 4. Reason :, The end correction must be applied for each open, end, i) A pipe closed at one end has only one open end., end correction = e, ii) A pipe open at both ends has two ends open, end correction = 2e, Q. 39) Two organ pipes closed at one end have, same diameters but different length. Show, , e, Where, l1 and l2 are vibrating lengths,, n1 and n2 are corresponding frequencies of, pipes close at one end., Ans., 1. We know, the fundamental frequency of pipe, closed atone end is,, , (Page17), , Superposition of waves
Page 19 :
n, , v, , Where, v = velocity of sound in air, l= length of air column, e = end correction, 2. The two organ pipes closed at one end have same, diameters and different lengths., Let, l1 = length of first pipe closed at one end, l2 = length of second pipe closed at one end, Therefore, equation (i) can be written as, .....(ii), v = 4n1 (l1 + e), v = 4n2 (l2 + e), ......(iii), From equation (ii) and (iii), we can write, 4n1(l2 + e) = 4n2(l2 + e), n1(l2 + e) = n2(l2 + e), n1 l2 + n1 e = n2l2 + n2 e, n1 l2 – n1 l2 = (n2 – n2) e, , n, , by –1, , e, e, , ., , Q.40) Explain the terms., Ans. a. Free vibrations :, When a body, capable of oscillating, is displaced, from its equilibrium position and released, it, makes oscillations which are called free, vibrations or free oscillations., In free vibrations. amplitude of oscillations, decreases due to air or frictional resistance and, finally it com.es to rest., 1. Examples :, i) Vibrations of the simple pendulum, when the bob, of a simple pendulum is displaced from stable, equilibrium position and released,, ii) Vibrations of prongs of tuning fork, when a, prong of a tuning fork is struck on a rubber pad., iii) Vibrations of stretched string if it is plucked at, some point, iv) Current oscillates in an LCR circuit when, capacitor discharges., 2. The frequency of free vibrations is called natural, frequency., 3. The natural frequency of vibrations depends on., i), The dimensions of the body, ii) Mass of the body, iii) Elastic properties and, 12th (Sci.), , iv) Mode of vibrations of the vibrating body., 4. If there is no restoring force acting on the, vibrating body, vibrations are truly free and the, amplitude will be constant., b. Forced vibrations, The vibrations of body under the action of, external periodic force in which body vibrate, with frequency equal to frequency of external, periodic fine (driving frequency) other than, natural frequency are called forced vibrations., 1. In forced vibrations, energy of vibrating body, remain constant., 2. In forced vibrations, frequency and amplitude of, forced vibrations are constant., 3. Frequency of forced vibrations is equal to the, frequency of external periodic force., 4. The amplitude of forced vibrations depends upon, i) Amplitude of applied force and damping force., ii) Difference between the frequency of external, periodic force and natural frequency of vibration, of body., The amplitude of forced vibration is small, when, the difference between frequencies of vibration, of body becomes large and vice versa., Q.41)Define and explain the phenomenon of, beats. Define waxing, waning, the period of, beats and beat frequency., Ans.:, Beats :, The production of alternate maxima .(waxing), and minima (waning) at point of medium due to, superposition of two sound waves of same, amplitude and nearly different frequency, travelling in the same direction, in the same, medium, is called phenomenon of beats., Explanation :, 1. If two sound notes (tuning fork) of equal, frequencies are sounded together, we hear a loud, sound of constant intensity., 2. If however, the frequencies of the notes are, slightly different and they are sounded together, we hear a sound note whose intensity is, alternately maximum and minimum., 3. In general, when two sound waves of nearly, equal frequencies (not exactly equal) and equal:, amplitudes, arrive at a point simultaneously, the, intensity of the resultant sound at the point varies, alternately and distinctly from maximum to, minimum, after definite intervals of time., 4. When the sound becomes loud (maximum), it is, said to wax, and when it becomes faint, (minimum) it is said to wane, a. Waxing :, The maximum intensity of sound (loud sound), is called waxing or maxima., In this case resultant amplitude is maximum., , (Page18), , Superposition of waves
Page 20 :
We know, Intensity $ A2. Therefore the resultant, intensity of sound will be maximum when, amplitude is maximum., Hence for waxing (loud sound), A = ± 2a (maximum), , b., , Waning :, The minimum intensity of sound (faint sound) is, called waning or minima., In this case resultant amplitude is minimum., One beat :, One waxing and adjacent waning form one beat., c. The period of beats (T) :, The time interval between two successive waxing, or waning is called the period of beats., d. Beat frequency (nb):, The number of beats heard per second is called, beat frequency., Q.42) Discuss analytically the formation of beats., Show that the beat frequency is equal to the, difference between the frequencies of the two, sound waves., Ans :, 1. Consider two sound waves of equal amplitude a, and slightly different frequencies n1 and n2 (with, n1 > n2) propagating through the same medium in, the same direction., 2. These waves can be represented by the, equations., , 3., , 4., , The period of heat i.e., time interval between two, successive waxing is, , Thus, period of beat is the reciprocal of, difference between the frequencies of two waves., , ....(i), y1 = a sin 2πn1t, ....(ii), and y2 = a sin 2πn2t, By the principle of superposition of waves, the, resultant displacement at the point is given by, y = y1 + y2, y = a sin 2πn1t + a sin2πn2t, y = a (sin 2πn1t + a sin2πn2t), Using the formula,, , Beat frequency (nb) =, , 8., , or y = A sin 2π Nt, where, , nb = n1– n2, Thus, the frequency of beat is equal to the, difference between the frequencies of the two, sound waves., Condition for waning (minimum sound):, The resultant intensity will be minimum when, the amplitude is zero., Hence for waning,, A = 0 (minimum), , ......(iv), , A=amplitude or resultant wave., N, 5., 7., , =resultant frequency., , Equation (iii) shows that resultant motion is a, S.H.M. with amplitude A., Condition for waxing :, , 12th (Sci.), , (Page19), , Superposition of waves
Page 21 :
1, , 3, , 5, 3., , of sound of one of the zero. When this is done,, both the instruments are emitting sound of the, same frequency. The instruments are then in, unison with each other., The phenomenon of beats can be used to produce, low frequency notes used in Jazz orchestra or, , Time period of beat i.e., time interval between, two successive waning is,, , western music., 4., , Beats are used to detect the presence of, dangerous gases in mines :, , i), Thus, period of beat is the reciprocal of, difference between the frequencies of two waves., , Air from a reservoir is blown through a pipe or, flute. Air from the mine is blown through another, similar pipe or flute., , Beat frequency, , ii) Speed of sound is different in different gases., Hence reservoir with different concentration than, , 9., , Thus,, Thus, period of beat is the reciprocal of, difference between the frequencies of two waves., From equation (v) and (vi), The time interval between two successive, 1, waxing or warning is equal to, ., , Thus waxing and warning occur periodically., Question bank:, 1. Explain the production of beats and deduce, analytically the expression for beat frequency.4M*, 2. What are beats? Show that the beat frequency is, equal to the difference between the frequencies, of the two sound notes giving rise to beats.-4M, 3. Derive an expression for the beat frequency by, analytical method., Q.43) Explain any two applications of beats. -2M, Ans., Applications of beats :, 1. The phenomenon of beats is used to determine, an unknown frequency :, i) The sound note of unknown frequency is, sounded simultaneously with a note of known, frequency which can be changed,, ii) The known frequency is so adjusted that beats, are heard,, iii) The, further adjustment is made till the beats, reduce to zero i.e., the frequency of the two notes, become equal., 2. For tuning musical instruments :, Musical instruments can b6 tuned by noting the, beats produced when two different instruments, are sounded together. By adjusting the frequency, 12th (Sci.), , air will sound slightly with different frequencies., iii) If no dangerous gases are present in the air from, the mine the two flutes will produce notes of the, same frequency and beats will not be heard iii., However if the air from the mine is polluted with, presence of dangerous gases, the two flutes will, produce notes of slightly different frequencies,, giving rise to beats, which serves as an early, warning system for safety., 5., , In modem day radio receiver incoming frequency, is superposed with a locally produced frequency, to produce intermediate frequency which is, always constant This makes tuning of the, receiver very simple This is used in super, heterodyne oscillators., , Q.44) Explain, , the, , following, , of sound : (1) loudness, , characteristics, , (2) pitch, , (3) quality, , or timbre., Ans., (1) Loudness : The loudness of a note is the, , (Page20), , magnitude of the sensation produced by the, sound waves on the ear. It depends upon (a) the, energy of the vibration (b) the sensitiveness of, the individual ear (c) the pitch of the sound., Superposition of waves
Page 22 :
The loudness of a sound depends on the, , [Note: A pure note, consisting of only one, , intensity of the sound wave, which is in turn, , frequency, is different from a musical note,, , proportional to the square of the amplitude of the, , which may be a combination of many different, , wave itself., , frequencies. A musical note has a fundamental,, , Loudness is a subjective sensation, while, , or lowest frequency, and superimposed on it are, , intensity is an objectively measurable physical, , higher frequencies, called overtones or partials., , property of the wave. There is no direct relation, , The number and relative strengths of the partials, , between loudness and intensity. Near the middle, , present determines the timbre of the note. The, , of the audible range of frequencies, the ear is, , ear always recognizes the fundamental as, , very sensitive to changes in intensity, which it, , determining the pitch of the note.], , interprets, as changes in loudness., , Q.45) Define intensity of sound. State its unit., , The unit of loudness is the phon. It is equal to, , Ans. Definition : The intensity of sound at a point is, , the loudness in decibel of any equally loud pure, , the time rate of flow of sound energy passing, , tone of J frequency 1000 Hz., , normally through a unit area at that point., , (2) Pitch : By pitch we mean whether the note is, , SI unit: the joule per second square metre, (j/s-m2) or watt per square metre (W/m2)., , high or low. The pitch of a note depends upon, the frequency of the sound. But pitch is not, , Q 46) What are the factors affecting the loudness, , determined by frequency alone. A physiological, , of sound ? Is intensity the same as loudness?, , factor is involved and the sense of pitch is, , Ans :, , modified by the loudness and quality of the, , (1) The factors affecting the loudness of sound are, , sound., , (i) the amplitude of the vibrations of the body, , The average range of frequencies that the, , (ii) the distance of the listener from the vibrating, , human ear detects as sound is approximately 20, , body (iii) the surface area of the vibrating body, , Hz to 20000Hz (the audible range). The human, , (iv) the density of the medium (v) the presence of, , ear is capable of detecting a difference in pitch, , the resonating bodies (vi) the sensitivity of the, , between two notes. The smallest difference in, , ear of the listener., , frequency that the ear can detect as a difference, , (2) Intensity and loudness are related, but not the, , in pitch is approximately proportional to the, , same. Intensity is a measurable quantity whereas, , frequency of one of the notes. That is, a given, , loudness is a sensation which is not measurable., , change in frequency of a low note will produce a, , Loudness depends on the intensity of sound as, , greater change in pitch than it will in a high note., , well as the sensitivity of the ear of the listener., , (3) Quality: By quality or timbre is meant that, characteristic of a sound by which it is possible, to distinguish it from all other sounds of the same, pitch and loudness. The same note played at the, same loudness on two different musical, instruments are easily distinguished from each, other by their timbre., , 12th (Sci.), , Q.47) Explain the term decibel, Ans. The intensity level of a sound wave, by, , (Page21), , definition, is, decibels as one decibel is 0.1 bel. Here, I0, (reference intensity) is taken as 10–12 W/m2., Superposition of waves
Page 23 :
Intensity level is expressed in decibel (dB)., , Ans., , There is no direct relation between loudness and, , (1) The frequency of sound determines its pitch. A, , intensity. The decibel is not a unit of loudness., , high pitched or shrill sound is produced by a, , [Note : The decibel, equal to 0.1 bel, is used for, , body vibrating with a high frequency and a low, , comparing two power levels, currents or, , pitched or flat sound is produced by a body, , voltages. The unit bel is named in honour of, , vibrating with a low frequency., , Alexander Graham Bell (1847-1922) BritishAmerican scientist, inventor of the v, , (2) Frequency is a measurable quantity whereas pitch, is not a measurable quantity., , telephone, , (1876).], , Q.50). Write a short note on Indian musical scale., , Q.48) What is the difference between a musical, , Ans: Indian music is chiefly based on melody, i.e.,, consonant notes in suitable succession. Besides, , sound and a noise?, Ans. A musical sound is pleasing to the listener, , this physiological sensation, there is a deep, , while al noise is not. The pleasure derived from a, , psychological involvement., , musical! note is because it strikes the ear as a, , The notes or svaras ( वर) used in an Indian, , perfectly] undisturbed, uniform sound which, remains unaltered as long as it exists. On the, , musical scale have the same musical intervals as, those of the major diatonic scale. The five, , other hand, noise is accompanied by a rapid,, , additional notes in pure intonation, ती, , irregular but distinc, alternations of various kinds, , and कोमल (flat) are also used. Thus, the choice is, , of sounds., , usually made from the following twelve svaras :, , A musical sound thus has a regularity or, , सा (shadja), रे (को) and रे (rishabha), ग(को) and, , smoothness because the vibrations that cause the, , ग(ga0ndha0ra), म, , and म(ती) (madhyam), प, , sound are periodic. But the converse, that if the, , (pancham),ध (को) and ध (dhaivata), नी(को) and, , vibrations are regular the sound is musical, is not, , नी (nishad), सा. However, as compared to the, , always true. For example, a ricking clock does, , fixed frequency of the tonic in western music, an, Indian vocalist or musician has the freedom to, set any frequency as the tonic. Besides, unlike, western music, dissonant intervals are sometimes, introduced to enhance the musical effect., However, the whole structure of Indian music, , not produce a musical note, or the definite note, produced by a card held against the teeth of a, rotating toothed wheel is far from being pleasant, to hear. Bearing such reservations in mind, the, essential difference between music and noise is, that the former is produced by periodic and, continuous vibrations, while noise results from, discontinuous sudden and sharp sounds with no, marked periodicity., Q49. (1) Which quantity out of frequency and, amplitude determines the pitch of the sound?, (2) Which out of pitch and frequency is a, , (sharp), , is based on ra0gas (राग), which are wellestablished melody types with a wide variety of, emotional content. They can be courageous,, amorous, melancholy, cheerful, soothing, or, ecstatic. Ra0gas are capable of conveying these, emotions to the listener and different ragas are, assigned to different seasons and different parts, of the day., , measurable quantity?, 12th (Sci.), , (Page22), , Superposition of waves
Page 24 :
Q.51) Which are the three broad types of musical, instruments?, Write a short note on types of musical, instruments., Ans. Musical instruments have been classified in, various ways. One ancient system that was based, on, , 'HLH, , the, , primary, , vibrating, , medium, , distinguished three main types of instruments :, stringed, wind and percussion., Examples :, (1) Stringed instruments (stretched strings) :, (a) Plucked : Tanpura, sitar, veena, guitar, harp, (b) Bowed: Violin, (c) Struck : Santoor, pianoforte, (2) Wind instruments :, (a) Free (air not confined): Harmonica or mouth, organ (without keyboard), harmonium (with, keyboard). (Both are reed instruments in which, free brass reeds are vibrated by air, blown or, compressed., (b) Edge (air blown against an edge): Flute, (c) Reedpipes : Saxophone (single reed), shehnai, and bassoon (double reeds), (3) Percussion instruments :, (a) Stretched skin heads: Tabla, mridangam,, (b) Metals (struck against each other or with ac, beater): Cymbals, Xylophone., , ****, , 12th (Sci.), , (Page23), , Superposition of waves