Page 3 :
GOVERNMENT OF KERALA, DEPARTMENT OF TECHNICAL EDUCATION, , APPLIED PHYSICS – I, FOR, DIPLOMA IN ENGINEERING, (Revision 2021), , Published by, STATE INSTITUTE OF TECHNICAL TEACHERS’, TRAINING & RESEARCH, KALAMASSERY, Email: [email protected], Website: www.sitttrkerala.ac.in, , i

Page 4 :
ii

Page 5 :
Preface, This book, drafted as per the revised syllabus and evaluation criteria of the Department of, Technical Education, Government of Kerala, is designed and prepared in compliance with the, State Institute of Technical Teachers' Training & Research (SITTTR). Outcome-Based, Education (OBE) adopted in technical education suggests the need for developing the abilities in, students that would enable them to grasp the concepts on their own rather than learn by heart the, complicated terms and definitions. Outcome-Based Education (OBE) also recommends that the, students should be able to apply the basic knowledge to solve engineering problems., , In, , preparing the book, great care has been taken to present the subject matter in a clear and simple, way keeping in mind the new approach to learning Physics as contemplated by Outcome Based, Education (OBE)., The book is divided into four chapters corresponding to four modules in the revised, syllabus. In each chapter, a considerable amount of conceptual learning sections, analytical, problems, and questions are included, to equip the students to face the newly introduced OBEbased internal evaluation as well as end semester examination. Small and simple sentences have, been used throughout the book to get rid of the hurdles of the English language. The diagrams, are neatly rendered and the mathematical steps are simplified. The revised syllabus and a model, question paper are also added at the end of the book. The content hopes to meet all the, requirements of science such as concepts, attitudes, creativity, and applications, and to make the, teaching and learning process interesting, understandable, and enjoyable for young minds. Much, pain has been taken to explain the difficult points in a manner that an average student can easily, grasp even the tough topics. The main strength of the book lies in the subject matter and the, experience that a student will get in solving problems of Physics. The conceptual learning, sections included will transcend the boundaries of the syllabus and hopes to enhance the, scientific aptitude of students., Suggestions and positive criticism for the improvement of this book from any quarter, would be thankfully accepted and will be applied in the next revised edition. This book will, fulfill the requirements of students and teachers of technical education. We hope that this book, will definitely deepen the interest of students., , Authors, iii

Page 7 :
Acknowledgments, We express our sincere gratitude to Sri. Tony E J, Joint Director, SITTTR and Sri. K M, Ramesh, former Joint Director, SITTTR. We express special gratitude to Smt. Chandrakantha A, S, Deputy Director, SITTTR who encouraged us in this venture. We are thankful to Smt. Swapna, K K, Project Officer, SITTTR for supporting us. We are also thankful to Dr. Wilson K C,, Assistant Professor of Physics, Maharajas College, Ernakulam for reviewing our book and, suggesting improvements to the contents of the book. We thankfully recognize all those who, inspired and helped us in this endeavor., , Authors, , v

Page 8 :
vi

Page 9 :
Table of Contents, , Page, iii, , Preface, Acknowledgment, , v, , Table of Contents, , vii, , Chapter 1: Measurements and Force, , 1, , 1.1 Measurements and Unit systems, 1.1.1 Physical quantities, 1.1.2 Unit of a physical quantity, 1.1.3 Fundamental quantities and derived quantities, 1.1.4 Unit systems, 1.1.5 CGS system, 1.1.6 MKS system, 1.1.7 System International (SI), 1.2 Errors in Measurements, 1.2.1 Systematic errors, 1.2.2 Random errors, 1.2.3 Least count error, 1.2.4 Absolute error, 1.2.5 Relative error, 1.2.6 Percentage error, 1.3 Basic Introduction to Vectors, 1.3.1 Graphical representation of vectors, 1.3.2 Collinear vectors, 1.3.3 Equal vectors, 1.3.4 Negative of a vector, 1.3.5 Unit vector, 1.3.6 addition of vectors, 1.3.7 Graphical methods of vector addition, 1.3.8 Analytical method for vector addition, 1.3.9 Subtraction of vectors, 1.3.10 Resolution of a vector, , vii, , 1, 1, 2, 2, 3, 3, 3, 3, 6, 6, 7, 7, 7, 8, 8, 10, 10, 11, 11, 11, 11, 11, 13, 14, 16, 16

Page 10 :
1.4 Kinematics, 1.4.1 Distance travelled and displacement, 1.4.2 Speed, 1.4.3 Velocity, 1.4.4 Acceleration, 1.4.5 Motion in one motion, 1.4.6 Equations of motion, 1.5 Dynamics, 1.5.1 Newton’s first law of motion, 1.5.2 Inertia, 1.5.3 Momentum, 1.5.4 Newton’s second law of motion, 1.5.5 Newton’s third law of motion, 1.5.6 Law of conservation of momentum, 1.5.7 Recoil of gun, 1.5.8 Rocket propulsion, 1.5.9 Impulse, , Chapter 2: Rotational Motion, , 20, 21, 21, 21, 22, 22, 22, 23, 23, 24, 25, 25, 26, 28, 30, 31, 32, 37, , 2.1 Basic types of motion, 2.2 Circular motion, 2.2.1 Angular displacement, 2.2.2 Linear velocity, 2.2.3 Angular velocity, 2.2.4 Linear acceleration, 2.2.5 Angular acceleration, 2.2.6 Relation between linear velocity and angular velocity, 2.2.7 Relation between linear acceleration and angular acceleration, 2.2.8 Period, 2.2.9 Centripetal acceleration, 2.2.10 Centripetal force, 2.2.11 Banking of roads, 2.2.12 Expression for angle of banking, 2.2.13 Banking of railway tracks, 2.3 Rotational motion of rigid bodies, 2.3.1 Moment of inertia, 2.3.2 Moment of inertia of a particle, 2.3.3 Moment of inertia of a rigid body, viii, , 37, 38, 39, 39, 39, 40, 40, 40, 41, 41, 43, 44, 45, 46, 46, 49, 49, 50, 50

Page 11 :
2.3.4 Radius of gyration, 2.3.5 Theorems on moment of inertia, 2.3.6 Moment of inertia of continuous mass distributions, 2.3.7 Torque, 2.3.8 Angular momentum, 2.3.9 Conservation of angular momentum, , Chapter 3: Work, Energy, and Power, , 51, 52, 52, 55, 57, 58, 61, , 3.1 Work, 3.1.1 Work in physics, 3.1.2 Types of work, 3.2 Energy, 3.2.1 Types of energy, 3.2.2 Different forms of energy, 3.2.3 Solar energy, 3.2.4 Transformation of energy, 3.2.5 Law of conservation of energy, 3.3 Power, 3.4 Friction, 3.4.1 Causes of friction, 3.4.2 Types of friction, 3.4.3 Laws of friction, 3.4.4 Advantages of friction, 3.4.5 Disadvantages of friction, 3.4.6 Methods to reduce friction, 3.5 Heat, 3.5.1 What is temperature?, 3.5.2 Temperature scales, 3.5.3 Conversion between temperature scales, 3.5.4 Thermometer, 3.5.5 Classification of thermometers, 3.5.6 Mercury thermometer, 3.5.7 Pyrometers, 3.5.8 Methods of heat transfer, 3.5.9 Specific heat capacity of a substance, , Chapter 4: Properties of Matter, , 61, 62, 62, 63, 63, 65, 67, 67, 69, 71, 75, 76, 76, 78, 78, 78, 79, 80, 80, 81, 82, 83, 83, 84, 84, 87, 90, 97, 98, , 4.1 Elasticity, ix

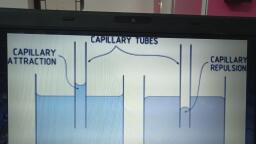
Page 12 :
4.1.1 Stress, 4.1.2 Strain, 4.1.3 Elastic limit, 4.1.4 Hooke’s law, 4.1.5 Young’s Modulus: Elasticity of length, 4.1.6 Rigidity modulus: Elasticity of shape, 4.1.7 Bulk modulus: Volume elasticity, 4.2 Pressure, 4.2.1 Pressure inside a fluid (hydrostatic pressure), 4.2.2 Atmospheric pressure, 4.2.3Gauge pressure and absolute pressure, 4.3 Surface Tension, 4.3.1 Surface energy of the liquid, 4.3.2 Cohesion and adhesion, 4.3.3 Angle of contact, 4.3.4 Capillarity, 4.3.5 Ascent formula, 4.3.6 Applications of surface tension, 4.3.7 Effect of temperature and impurities on surface tension, 4.4 Fluid dynamics, 4.4.1 Streamline flow and turbulent flow, 4.4.2 Reynold’s number, 4.4.3 Continuity equation in fluid dynamics, 4.4.4 Energies of a flowing fluid, 4.4.5 Bernoulli’s theorem, 4.4.6 Applications of Bernoulli’s theorem, 4.5 Viscosity, 4.5.1 Coefficient of viscosity, 4.5.2 Terminal velocity, 4.5.3 Stoke’s law, Bibliography, , 99, 99, 99, 99, 100, 101, 103, 108, 108, 109, 110, 112, 113, 114, 114, 116, 116, 117, 118, 118, 118, 120, 120, 125, 127, 128, 130, 131, 131, 132, , Revised Syllabus, , 138, , Model question paper, , 143, , x, , 137

Page 13 :
Applied Physics - !, , CHAPTER 1, MEASUREMENTS AND FORCE, 1.1 MEASUREMENTS AND UNIT SYSTEMS, , Conceptual Learning 1.1, Find the values of the following quantities in proper units, 1. Your height, 2. Your mass, 3. Distance from home to college, 4. How long do you study per day?, , Three students were asked to measure the length of a table. The students reported the, measured values as 3, 91.44,and 36. It may look wrong. Actually, the three students used, different units for the measurement. The correct values are 3ft, 91.44cm, and 36inches. Without, units, the value of a measurement is meaningless. All values of measurements should be, represented with a proper unit. In the following section, we discuss measurable quantities and, what the unit of a quantity means., , 1.1.1 Physical quantities, What do we mean by a physical quantity? Why length, mass, and time are physical, quantities, and taste and smell are not? It is possible to measure length, mass, and time using, instruments such as meter scale, physical balance, stopwatch, etc. But taste and smell cannot be, measured using any instruments. Physical property related to a substance or phenomenon which, State Institute of Technical Teachers’ Training & Research, , |, , Page, , 1

Page 14 :
Applied Physics - !, , can be quantified by measurement is called a physical quantity. The measured value of a, physical quantity is expressed as the combination of a number and a unit., , 1.1.2 Unit of a physical quantity, Physics describes the laws of nature. This description is quantitative and involves the, measurement of physical quantities. How do you measure the length of a table? We compare the, length of the table to a standard value of length and find out how many times the standard value, has been repeated. In general, to measure a physical quantity its value has to be compared with a, standard value of that quantity. The standard used for the measurement of a physical quantity is, called its unit. The standard corresponds to exactly one unit of that quantity. The measured, value of the physical quantity is expressed in terms of the unit of that quantity. The measured, value of a quantity is expressed in two parts. The first part gives how many times the given unit, has been repeated and the second part gives the name of the unit., Table 1.1 Examples of some physical quantities in suitable units, Quantity measured, , Unit used, , Multiple of unit, , Measured value, , Length of table, , m, , 2.5, , 2.5m, , Speed of a car, , km/hr, , 60, , 60km/hr, , Volume of milk, , litre, , 2, , 2 litres, , Voltage of a battery, , volt, , 1.5, , 1.5volt, , Body temperature, , Fahrenheit, , 97. 6, , 97.6 Fahrenheit, , 1.1.3 Fundamental quantities and derived quantities, There are a large number of physical quantities and each physical quantity requires a, separate unit for its specification. However, most of them are interrelated. For example, if a unit, of length is defined, a unit of area is automatically obtained. There are only a few independent, quantities. Physical quantities which are defined by the process of measurement and independent, of other quantities are called fundamental quantities. All other quantities can be expressed in, State Institute of Technical Teachers’ Training & Research, , |, , Page, , 2

Page 15 :
Applied Physics - !, , terms of these fundamental quantities. Quantities derived from fundamental quantities are called, derived quantities. The unit of fundamental quantities are called fundamental or base units and, those of derived quantities are called derived units. Examples of fundamental and derived, quantities along with their units are given in the table below:, Table 1.2 Examples of fundamental and derived quantities along with their units, Fundamental quantity, , Unit, , Length, , meter (m), , Time, , second (s), , Mass, , kilogram (kg), , Derived quantity, Area, Volume, Velocity, Acceleration, Density, Momentum, , Unit, m2, m3, m/s, m/s2, kg/m3, kg m/s, , 1.1.4 Unit systems, The complete set of units of all physical quantities forms a unit system. There are several, unit systems in use over the world and each unit system is based on a different set of, fundamental quantities.CGS system, MKS system, and SI system are examples of unit systems., , 1.1.5 CGS system, CGS system is a unit system based on three fundamental quantities namely length, mass,, and time. In the CGS system, centimeter (cm), gram (g), and second (s) are the units of length,, mass, and time respectively., , 1.1.6 MKS system, MKS unit system has meter (m), kilogram (kg), and second (s) as base units respectively, for the three fundamental quantities - length, mass, and time., , 1.1.7 System International (SI), In 1971, General Conference on Weight and Measures (CGPM) held its meeting and, decided on a system of units by international agreement. This system is known as System, State Institute of Technical Teachers’ Training & Research, , |, , Page, , 3

Page 16 :
Applied Physics - !, , International and is abbreviated as SI. The SI system is based on seven fundamental quantities, and its units. Units of all derived quantities can be obtained by multiplying and dividing seven, base units, with no numerical factors involved., Table 1.3 Fundamental quantities and their units in SI unit system, Fundamental quantity, , Unit, , Symbol, , Length, , meter, , m, , Mass, , kilogram, , kg, , Time, , second, , s, , Electric current, , ampere, , A, , Temperature, , kelvin, , K, , Amount of substance, , mole, , mol, , Luminous intensity, , candela, , cd, , Units of all derived quantities can be obtained from the seven fundamental units given in, table 1.3. SI unit system classified plane angle and solid angle as supplementary quantities. The, SI unit of plane angle is radian (rad) and that of solid angle is steradian (sr). But the notion of, supplementary quantities was abandoned in 1995 and classified them also as derived quantities., , Conceptual Learning 1.2, 1. A commonly used unit of length is foot. One foot is equal to 12inches. Measure the, length and breadth of any room of your house in the unit of meters and convert it into, feet. Hence calculate the area of the room in the units of metre 2 and feet2 (sq.ft)., 2. The volume of liquids is usually represented in litres. A water tank has dimensions of, 2m length, 1 m breadth, and 1m height. Calculate the capacity of the tank in litres., , State Institute of Technical Teachers’ Training & Research, , |, , Page, , 4

Page 17 :
Applied Physics - !, , It is convenient to represent large and small quantities in the SI system in terms of multiple, and sub-multiple of 10. Standard prefixes are used for certain powers of 10 as shown in table 1.4., Table 1.4 Prefixes used for multiples and submultiples in SI unit system, Prefix, , Multiple, , Symbol, , Prefix, , Sub- multiple, , Symbol, , deca, hecto, kilo, mega, giga, tera, peta, exa, , 101, 102, 103, 106, 109, 1012, 1015, 1018, , da, h, k, M, G, T, P, E, , deci, centi, milli, micro, nano, pico, femto, atto, , 10-1, 10-2, 10-3, 10-6, 10-9, 10-12, 10-15, 10-18, , d, c, m, µ, n, p, f, a, , Conceptual Learning 1.3, Express the following in given units, 2.43 x 10-2 m, , 1) 2.43 cm, , =, , 2) 14.3 cm, , = …………… m, , 3) 7.00 cm, , = ……………m, , 4) 5 mm, , = ……………m, , 5) 24.5 mm2 = ……………m2, 6) 18.4 cm3= …………….m3, 7) 22 mm3 = ……………m3, 8) 12 cm2= ……………m2, 9) 50g, , = ……………kg, , 10) 150 g/cm3= ……………kg/m3, 11) 36 km/hr =………………m/s, 12) 8 litres =………………m3, 13) 2.48cm2= ………………m2, , State Institute of Technical Teachers’ Training & Research, , |, , Page, , 5

Page 18 :
Applied Physics - !, , 1.2 ERRORS IN MEASUREMENTS, Measurement of various physical quantities is fundamental to the study of science and, engineering. The value of every measurement contains some uncertainty. This uncertainty is, called error. The difference between the true value and the measured value of a quantity is, known as the error of measurement. Errors in measurements can be classified into two, categories. They are systematic errors and random errors., , 1.2.1 Systematic Errors, Systematic errors in measurements can be due to instrumental errors, incorrect, experimental techniques, and personal errors., a) Instrumental errors: These errors arise from the imperfect design or calibration of, instruments, zero error of instruments, etc. Zero error in vernier calipers or screw, gauge and error due to measurement of length using a scale broken at one end are, examples of instrumental errors., , b) Error due to incorrect experimental technique: These kinds of errors occur due to, inaccurate experimental procedures as well as external factors like pressure,, temperature, humidity, wind, etc. For example, measurement of body temperature by, placing a thermometer under the armpit results in a lower temperature value than the, actual value., , c) Personal errors: Such errors arise due to personal bias, lack of proper setting of the, apparatus, or individual’s carelessness in taking observations. These types of errors, are also known as observational errors. For example, when an observer holds his head, towards the right (by habit) while reading the position of a needle on the scale, he, introduces an error due to parallax., The systematic errors tend to be in one direction, either positive direction or negative, direction with respect to the true value. This type of error can be minimized by using better, instruments, improving experimental techniques, and avoiding personal bias., , State Institute of Technical Teachers’ Training & Research, , |, , Page, , 6

Page 19 :
Applied Physics - !, , 1.2.2 Random Errors, Random errors come from unpredictable changes in experimental conditions. The, magnitude and direction of these errors vary randomly with each measurement. Random errors are, present in all experiments and are unpredictable. The random errors can be reduced by taking a, greater number of measurements. These errors are also called statistical errors and can be removed, by statistical methods like averaging. For example, unpredictable temperature changes can affect, the electrical properties of instruments in an experiment involving electrical instruments., , 1.2.3 Least Count Error, The least count error is the error associated with the resolution of the instrument. The, smallest value that can be measured by a measuring instrument is called its least count. All, readings or values are good only up to this value. For example, a vernier caliper has the least, count of 0.01 cm and a screw gauge has a least count of 0.001 cm. Using instruments of higher, precision, improving experimental techniques, etc., we can reduce the least count error., Repeating the observations several times and taking the arithmetic mean of all the observations,, the mean value would be very close to the true value of the measured quantity., , 1.2.4 Absolute error, Let𝑎 , 𝑎 , 𝑎 , . . . . . . . . . , 𝑎 be the values obtained for a physical quantity ‘a’ in an, experiment repeated ‘n’ times. The arithmetic mean of the values is taken as the true value. The, arithmetic mean is, 𝑎, , =, , a, , a, , ………., , a, , n, , The absolute error of a measurement is the difference between the individual, measurement and the true value of that quantity. It is denoted as|∆𝑎|.Then errors in individual, measurements are, ∆𝑎 = 𝑎, , − 𝑎, , ∆𝑎 = 𝑎, , − 𝑎, , ……, , ……, , ….., , ……, , ……, , ….., , ∆𝑎 = 𝑎, State Institute of Technical Teachers’ Training & Research, , − 𝑎, |, , Page, , 7

Page 20 :
Applied Physics - !, , ∆𝑎 calculated may be positive or negative, but absolute error |∆𝑎| is always positive.The, arithmetic mean of all absolute errors of all the measurements is taken as the mean absolute error, of the physical quantity ‘a’. It is denoted as ∆𝑎, ∆𝑎, , ., , = (|∆𝑎 | + |∆𝑎 | + |∆𝑎 | … … … . + |∆𝑎 |)/𝑛, , The value of the physical quantity ‘a’ can be written as, 𝑎= 𝑎, , ± ∆𝑎, , 1.2.5 Relative error, The ratio of mean absolute error,∆𝑎, , to the mean value, 𝑎, , of the physical, , quantity measured is called the relative error., Relative error =, , ∆, , 1.2.6 Percentage error, The relative error of a physical quantity expressed in percentage is called percentage, error., Percentage error =, , ∆, , × 100 %, , Conceptual Learning 1.4, Measure the length and breadth of your study table and calculate its area. Repeat these, measurements five times and calculate the area in each case. (Use the scale available in your, instrument box for measurements), i) Find out the absolute error, relative error, and percentage error in length, breadth,, and area of the table., ii) Can you relate relative errors in the area of the table with relative errors in the length, and breadth of the table?, , State Institute of Technical Teachers’ Training & Research, , |, , Page, , 8

Page 21 :
Applied Physics - !, , Example 1.1, The measurement of length gives values of 2.54cm, 2.51cm, 2.48cm, 2.55cm, and 2.52cm. Find, the absolute error, relative error, and percentage error., Solution:, ., , Mean length =, , ., , ., , ., , ., , = 2.52 cm, , Absolute errors:, |Δa1| = |2.54-2.52| = 0.02, |Δa1| = |2.51-2.52| = 0.01, |Δa1| = |2.48-2.52| = 0.04, |Δa1| = |2.55-2.52| = 0.03, |Δa1| = |2.52-2.52| = 0, Mean absolute error =, , |∆, , | |∆, , |, , …………. |∆, , |, , = (0.02+0.01+0.04+0.03+0)/5, = 0.02, Relative error =, , ∆, , =, , Percentage error=, , ., , = 0.008, , ., ∆, , ×100 % = 0.8 %, , Example 1.2, The mean absolute error of a set of measurements is 0.85 and the mean value is 12.6. Find the, relative error and percentage error., Solution:, Mean absolute error, ∆𝑎, Mean value,amean= 12.6, Relative error =, , ∆, , Percentage error =, , =, ∆, , = 0.85, , ., ., , = 0.07, , × 100 = 0.07 × 100 = 7 %, , State Institute of Technical Teachers’ Training & Research, , |, , Page, , 9

Page 22 :
Applied Physics - !, , 1.3 BASIC INTRODUCTION TO VECTORS, Physical quantities can be classified into two categories. Some quantities can be, completely described by its magnitude alone. Quantities having only magnitude are called scalar, quantities. Mass, time, temperature, and potential energy are examples of scalar quantities., Quantities having both magnitude and direction are called vector quantities. A vector quantity, requires both magnitude and direction to describe it completely. Force is an example. What, happens when a force of 10N acts on a body lying on a surface can be answered only if the, direction of application of the force is known. A force acting in the downward direction produces, no effect on the body, whereas a horizontal force produces an acceleration., A vector quantity is denoted either using bold letters (v, F) or putting a small, arrow → , → on the top of the symbol used for the representation of the quantity. The, magnitude of a vector quantity, say F, is denoted by |F| or F., , Conceptual Learning 1.5, 1. Name any five vector quantities and five scalar quantities, 2. State whether the result of the following operation is a vector or a scalar, a) Multiplication of two scalars, b) Multiplication of a vector with a scalar, , 1.3.1 Graphical representation of a, vector, A vector quantity is represented, graphically by a straight line with an, arrowhead as shown in Fig. 1.1. The length, of the straight line represents the magnitude, of the vector and the arrowhead gives the, direction of the vector. The end having the, , Fig. 1.1 Geometric representation of a vector, , State Institute of Technical Teachers’ Training & Research, , |, , Page, , 10

Page 23 :
Applied Physics - !, , arrow mark is called the head and the other end is called the tail of the vector., A vector can be displaced parallel to itself. Moving a vector parallel to itself does not, change the magnitude and direction of the vector., , 1.3.2 Collinear vectors, Two or more vectors lying on the same line are called collinear vectors. They can have, the same or different magnitude and the direction can be either the same or opposite., , 1.3.3 Equal vectors, Two vectors of the same magnitude and direction are called equal vectors., , 1.3.4 Negative of a vector, The negative of a vector is defined as another vector having the same magnitude but, opposite in direction to the given vector., , 1.3.5 Unit vector, A unit vector is a vector of unit magnitude and points in a particular direction. It is used, just to specify a direction and hence it is also called a direction vector. A unit vector is denoted, by a cap or hat symbol above a letter. A vector divided by its magnitude gives the unit vector in, the direction of the given vector. Unit vector, 𝑎 in the direction vector, 𝐴⃗ is given by, , 𝐴⃗, 𝑎=, |𝐴⃗|, The commonly used unit vectors are 𝚤, 𝚥̂ and 𝑘 which indicates X, Y, and Z directions, respectively., , 1.3.6 Addition of vectors, Consider two boys pushing a table with equal forces (say 10N) in the same direction as, shown in Fig. 1.2 (a). The table easily moves in the direction of the pushing force. Now, consider, the forces are applied in the opposite direction as shown in Fig. 1.2 (b), the table doesn’t move., In the first case, the two forces added up since they are in the same direction, and in the second, State Institute of Technical Teachers’ Training & Research, , |, , Page, , 11

Page 24 :
Applied Physics - !, , case, the two forces cancel each other. Again, if the two forces are applied at the two adjacent, sides of the table, the motion of the table can be found by adding the two forces mathematically., , Fig. 1.2 (a) Two boys pushing a table in the same direction, (b) Two boys pushing a table in the opposite direction, , Conceptual Learning 1.6, Force is a vector quantity. Add following pairs of forces which are either parallel or, antiparallel., , 1. 16 N, , + 6N, , 2., , 5N, , +, , 3., , 5N, , +, , 4. 4 N, , + 2N, , =, , 5N, 3N, , =, =, , =, , The addition of two scalar quantities can be done using the rules of ordinary algebra. Sum, of two masses, which is a scalar quantity, say 10kg and 10kg always give 20kg. But in the case, State Institute of Technical Teachers’ Training & Research, , |, , Page, , 12

Page 25 :
Applied Physics - !, , of vector quantities, we have to take care of direction also. The result of the addition of two or, more vector quantities is called vector sum or resultant. The addition of two vectors can be done, mathematically by using graphical methods or analytical methods., , 1.3.7 Graphical methods for vector addition, In the graphical method, we use the graphical representation of vectors to find the resultant of, two vectors. The resultant of two non-parallel vectors can be obtained graphically by two, methods; triangle method and parallelogram method., (a) Triangle method of vector addiction, The triangle method is based on the triangular law of vector addition. The triangular law of, vector addition states that if two vectors are represented by the adjacent sides of a triangle taken, in order, then the resultant vector is represented both in magnitude and direction by the third, side of the triangle taken in the reverse order., , Fig. 1.3 Addition of two vectors by triangular method, , Let 𝐴⃗and 𝐵⃗ are two non-parallel vectors. To find the vector sum using the triangle, method, place the vectors such that the tail of one vector coincides with the head of the other, vector as shown in Fig. 1.3. Complete the triangle by drawing the third side. The third side gives, the resultant vector𝑅⃗ ., , State Institute of Technical Teachers’ Training & Research, , |, , Page, , 13

Page 26 :
Applied Physics - !, , (b) Parallelogram method of vector addition, This method is based on the parallelogram law of vector addition. The parallelogram law, of vector addition states that if two vectors are represented both in magnitude and direction by, the two sides of a parallelogram drawn from a point, then the resultant vector is represented, both in magnitude and direction by the diagonal of the parallelogram passing through the point., , Fig. 1.4 Addition of two vectors by parallelogram, method, , In this method, the two vectors are placed such that their tails coincide as shown in, Fig.1.4. A parallelogram is formed by drawing two lines parallel to the given vectors. The, diagonal of the parallelogram passing through the common point of the two vectors is the, resultant vector., , 1.3.8 Analytical method for vector addition, The, graphical, method, provides a good visual understanding, of the process of vector addition. But, it is time-consuming and has less, accuracy. Alternately the resultant, vector can be found using the, analytical method. Consider two, vectors 𝐴⃗and 𝐵⃗. Let θ be the angle, between, , the two vectors. The, resultant, 𝑅 ⃗, of the two vectors can, , Fig. 1.5 Resultant of two vectors acting at an angle, , , State Institute of Technical Teachers’ Training & Research, , |, , Page, , 14

Page 27 :
Applied Physics - !, , be obtained by the parallelogram method as shown in Fig. 1.5., The magnitude of the resultant vector R is given by the expression, , R=, , A + B + 2ABcosθ, , The direction of the resultant vector is specified by the angle α with respect to the vector 𝐴⃗., The angle α is given by the expression, , 𝛼 = 𝑡𝑎𝑛, , 𝐵 𝑠𝑖𝑛𝜃, 𝐴 + 𝐵 𝑐𝑜𝑠𝜃, , Special cases:, a) If two vectors are in the same direction, then θ = 0 and hence, 𝑐𝑜𝑠𝜃 = 1, The magnitude of the resultant,R = √A + B + 2ABcosθ, R= √A + B + 2AB, R= (A + B), R=𝐴+𝐵, The magnitude of the resultant is the sum of the magnitudes of the two vectors., b) If two vectors are in opposite direction, then θ = 180o and hence, 𝑐𝑜𝑠𝜃 = −1, The magnitude of the resultant, R = √A + B + 2ABcosθ, R= √A + B − 2AB, R= (A − B), R=𝐴−𝐵, The magnitude of the resultant is the difference of the magnitudes of the two vectors., , State Institute of Technical Teachers’ Training & Research, , |, , Page, , 15

Page 28 :
Applied Physics - !, , Conceptual Learning 1.7, Consider two vectors, 𝐴⃗and 𝐵⃗ of magnitudes 4 units and 2 units. The angle between the, vectors is 60o. Find out the magnitude and direction of the resultant of the two vectors by, i) Triangular method, ii) Parallelogram method, iii) Analytical method, , 1.3.9 Subtraction of vectors, Subtraction of two vectors also involves addition. To subtract𝐵⃗ from 𝐴⃗first, take the, negative of 𝐵⃗ and then add it to𝐴⃗. Hence, subtraction of two vectors is the same as the addition, of a vector with the negative of the second vector., 𝐴⃗ − 𝐵⃗ = 𝐴⃗ + (−𝐵⃗), , Fig. 1.6 Subtraction of two vectors, , 1.3.10 Resolution of a vector, Two or more vectors can be combined to form a single vector through addition., Similarly, a given vector can be represented as the sum of two or more vectors acting along, different directions. The process of splitting a given vector into two or more vectors along, different directions is called the resolution of a vector. The vectors obtained by the resolution of, the given vector are called component vectors., , State Institute of Technical Teachers’ Training & Research, , |, , Page, , 16

Page 29 :
Applied Physics - !, , Consider a vector lying in the northwest direction as Fig. 1.7 (a). It can be considered to, have two components – a northward component and a westward component. Similarly, an, upward and rightward vector has an upward component and a rightward component as, Fig. 1.7 (b)., , Fig. 1.7 (a) Components of a northwest vector, (b) Components of an upward and rightward vector, , State Institute of Technical Teachers’ Training & Research, , |, , Page, , 17

Page 30 :
Applied Physics - !, , A vector lying in a plane is usually, resolved along two mutually perpendicular, directions. The resolution of a vector along, mutually perpendicular directions is called, rectangular resolution. The two perpendicular, components are called rectangular components., The rectangular components are taken along the, X-axis and Y-axis.Consider a vector 𝐴⃗making, an angle θ with the X-axis. Draw perpendiculars, from the head of the vector 𝐴⃗ to X-axis and Yaxis to meet at the points P, , and Q, , Fig. 1.8 Rectangular resolution of a vector, , respectively.Then, if OP and OQ are taken as two vectors 𝐴 ⃗and𝐴 ⃗ respectively, then by, parallelogram law of vector addition, 𝐴⃗is the resultant vector., 𝐴⃗ = 𝐴 ⃗ + 𝐴 ⃗, Thus, , and 𝐴 ⃗and𝐴 ⃗ are vector components of𝐴⃗.Magnitudes of 𝐴 ⃗and𝐴 ⃗are, , called scalar components. 𝐴 and 𝐴 are called x-component and y-component respectively., Using simple trigonometric relations, x-component and y-component of vector 𝐴⃗ is given by, 𝐴 = 𝐴 𝑐𝑜𝑠𝜃, 𝐴 = 𝐴 𝑠𝑖𝑛𝜃, Now let us examine two real-life examples of the resolution of vectors., a) Walking: While walking, a person applies a force on the ground and the reaction force, by the ground on the man enables him to move forward. The force applied by the man is, directed at an angle with the horizontal. The reaction force by the ground is opposite in, direction to the applied force. The reaction force R can be resolved along horizontal and, vertical components as shown in Fig. 1.9. The horizontal component pushes him, forward., , State Institute of Technical Teachers’ Training & Research, , |, , Page, , 18

Page 31 :
Applied Physics - !, , Fig. 1.9 Resolution of reaction force exerted by the ground on a walking, man, b) Pulling a cart: Consider a man pulling a cart. The force is directed at an angle with the, horizontal. Here the force can be resolved into two components – vertical and horizontal, components as shown in Fig. 1.10. The horizontal component is responsible for the, motion of the cart., , Fig. 1.10 Resolution of pulling force applied on a cart, , State Institute of Technical Teachers’ Training & Research, , |, , Page, , 19

Page 32 :
Applied Physics - !, , Conceptual Learning 1.8, Resolve the given forces along x-direction and y-direction., 1., 12 N, 30o, , 2., , 20 N, 60, , 3., , o, , 8N, 45o, , (a) x- component = ------- N, (b) y-component = -------- N, , (a) x- component = ------- N, (b) y-component = -------- N, , (a) x- component = ------- N, (b) y-component = -------- N, , 1.4 KINEMATICS, The motion of objects can be found everywhere around us. The study of motion is basic, to physics. When do we say that a body is at rest or in motion? An object is at rest if its position, changes with time. An object is said to be in motion if its position changes with time. But when, do we say that an object is changing its position? Consider a book in the hand of a boy sitting in, a moving bus. The book is at rest with respect to an observer on the bus, whereas with respect to, an observer on the road, the book is in motion. The concept of rest and motion are relative to the, observer. There is no absolute motion or absolute rest., Mechanics is a branch of physics that deals with the study of the motion of bodies, its, causes, and effects. Kinematics is a branch of mechanics that describes the motion of objects, without considering the causes of motion. In kinematics, motion is mathematically described in, terms of distance, displacement, speed, velocity, acceleration, and time., , State Institute of Technical Teachers’ Training & Research, , |, , Page, , 20

Page 33 :
Applied Physics - !, , 1.4.1 Distance travelled and Displacement, Consider a particle initially at, position A, it travels and reaches point, B through the path ACB. Distance is, defined as the total length of the path, travelled by a particle. Here the, length, , ACB, , gives, , the, , distance, , travelled. Distance is a scalar quantity, and its unit is meter. We are more interested in the change in position of the particle, which is, specified by the term displacement. Displacement is defined as the shortest path length between, the final position and the initial position of the particle. The straight-line path from A to B gives, the displacement. Displacement is a vector quantity having both magnitude and direction. The, length of the straight line gives the magnitude of the displacement and the direction is from the, initial position to final position. The SI unit of displacement is also meter., , 1.4.2 Speed, The speed of a particle is related to the distance travelled. Speed is the distance travelled, by a body in unit time., 𝑠𝑝𝑒𝑒𝑑 =, , 𝑑𝑖𝑠𝑡𝑎𝑛𝑐𝑒, 𝑡𝑖𝑚𝑒, , Speed is a scalar quantity and its unit is m/s, , 1.4.3 Velocity (v), The velocity of a particle denotes how fast it is changing its position. The displacement of, a body in unit time is called velocity., 𝑑𝑖𝑠𝑝𝑙𝑎𝑐𝑒𝑚𝑒𝑛𝑡, 𝑡𝑖𝑚𝑒, 𝑠, 𝑣=, 𝑡, , 𝑣𝑒𝑙𝑜𝑐𝑖𝑡𝑦 =, , Velocity is a vector quantity and its unit is m/s., , State Institute of Technical Teachers’ Training & Research, , |, , Page, , 21

Page 34 :
Applied Physics - !, , 1.4.4 Acceleration (a), The rate of change of velocity of a body is called acceleration. Since velocity is a vector, quantity, a change in its magnitude or direction or both gives accelerated motion., 𝑐ℎ𝑎𝑛𝑔𝑒 𝑖𝑛 𝑣𝑒𝑙𝑜𝑐𝑖𝑡𝑦, 𝑡𝑖𝑚𝑒, 𝑣−𝑢, 𝑎=, 𝑡, , 𝑎𝑐𝑐𝑒𝑙𝑒𝑟𝑎𝑡𝑖𝑜𝑛 =, , where u is the initial velocity and v is the final velocity of the body. Acceleration is a, vector quantity and its unit is m/s2., , 1.4.5 Motion in one dimension, The motion of an object along a straight-line path is called motion in one dimension.A, particle in one-dimensional motion has only two directions of motion (either left or right, upward, or downward, east or west, etc.). To specify the directions of the vector quantities displacement,, velocity, and acceleration we use the signs + and - to denote the two directions., If the velocity of the body remains a constant in one-dimensional motion, then it is called, uniform motion. In uniform motion, the magnitude and direction of velocity remain constant and, hence its acceleration is zero.The motion of a car along a straight road, a ball thrown vertically, upwards, a freely falling body are some of the examples of motion in one dimension. A, uniformly accelerated motion is one in which the acceleration of the particle remains constant., , 1.4.6 Equations of motion, Consider the motion of a particle with initial velocity ‘u’ and uniform acceleration ‘a’., Let the displacement and velocity of the particle after a time ‘t’second is ‘s’ and ‘v’ respectively., The motion of the particle along a straight-line path with uniform acceleration can be analyzed, using the three equations of motion., v = u + at, 1, s = ut + at, 2, v = u + 2as, State Institute of Technical Teachers’ Training & Research, , |, , Page, , 22

Page 35 :
Applied Physics - !, , 1.5 DYNAMICS, Dynamics is a branch of mechanics that deals with the study of forces and its effect on, the motion of bodies. In dynamics, Newton's laws of motion are three laws that describe the, relationship between the motion of an object and the forces acting on it., , 1.5.1 Newton’s first law of motion, Newton’s first law of motion states that everybody continues in its state of rest or of, uniform motion along a straight line unless compelled by some external force to change that, state., , Conceptual Learning 1.9, Consider a cricket ball placed at one end of a very long horizontal straight-line track. A force, is applied just to start the motion of the ball along the track. Now answer the following, questions based on your experience and check whether our common experience contradicts, Newton’s first law of motion., 1. Do we need to apply force all the time to keep the ball in motion?, 2. Will the ball stop after some time? Does this observation contradict Newton’s first law, of motion?, 3. Is there any external force acting on the body to stop it?, , Conceptual Learning 1.10, Imagine that you are going to drive a car which is at rest. From Newton’s first law, we know, that an external force is required to change the state of the rest of a body. The rotating force, acting on the wheels of the car is provided by the engine and it is an internal force. Does the, motion of the car contradict Newton’s first law of motion? Explain your answer., Newton’s first law only provides a mere definition of the force, but it doesn’t provide any, means to measure the force acting on a body. Force can be defined as any agency which can, change the state of rest or uniform motion of a body. The first law of motional so implies that the, State Institute of Technical Teachers’ Training & Research, , |, , Page, , 23

Page 36 :
Applied Physics - !, , state of rest and the state of uniform motion are the same. In both the state the acceleration of the, body is zero. A force is needed to produce an acceleration of a body. A body in uniform motion, continues its motion with constant velocity if no force acts on it. A body in motion doesn’t mean, that a force is acting on it. Only accelerated motions require a force. In most situations, more, than one force acts on a body and still, its acceleration may be zero. It is the net force that, decides the state of the body. If the net force is zero, the body should be either in rest or in, uniform motion., , 1.5.2 Inertia, Inertia is the resistance of a body to any change in its state of rest or uniform motion, along a straight line. In the absence of a net external force, a body at rest continues to remain at, rest and a body in motion continues to move with constant velocity. Newton’s first law of, motion is also known as the law of inertia. Inertia is an inherent property of all bodies. Nobody, can change its state of motion by itself and only an external force can change its state of motion., As we know from experience, some objects have more inertia than others. For example, it, is obviously more difficult to change the motion of a large almirah than that of a basketball. The, higher the mass, the higher will be the inertia. The inertia of an object is measured by its mass., The tendency of a body to remain in its existing state of rest is called inertia of rest. The, tendency of a body to remain in its existing state of motion with constant velocity is called, inertia of motion. A few real-life examples of inertia of rest and inertia of motion are given, below., a), , A person standing in a stationary bus falls backward when the bus starts suddenly. This, is because the lower part of his body moves forward with the bus, but the upper part of, his body remains at rest due to inertia of rest, which results in the backward fall., , b), , A person trying to get down from a moving bus falls forward. The lower part suddenly, comes to rest on touching the ground, but the upper part of his body remains in motion, due to inertia of motion and the person falls forward., , c), , Fruits from a tree fall due to inertia of rest when the tree is shaken. Both the fruits and, branches are at rest, but when shaken branches start moving whereas fruits remain in its, state of rest and are separated from the branches., , State Institute of Technical Teachers’ Training & Research, , |, , Page, , 24

Page 37 :
Applied Physics - !, , 1.5.3 Momentum (p), Momentum is the quantity of motion of a body. The momentum of a body is defined as the, product of mass and velocity. It is a vector quantity and its unit is kg m/s. If a body of mass ‘m’, moving with a velocity ‘v’, then its momentum is given by, 𝑝 = 𝑚𝑣, The momentum of a body at rest is zero. Consider a cricket ball and tennis ball which is, lighter in mass compared to a cricket ball moving with the same velocity. The momentum of the, cricket ball is higher due to its large mass. It is easier to catch the tennis ball than the cricket, ball. A cricket ball requires more force to stop than a tennis ball. Thus, force is related to, momentum or more specifically change in momentum. Newton’s second law gives the relation, between force and momentum., , Conceptual Learning 1.11, Identify the body having the highest momentum, 1. A car of mass 800kg moving with velocity 30m/s, , 2. A truck of mass 2000kg moving with velocity 10m/s, 3. A motorcycle of mass 150kg moving with velocity 40m/s, , 1.5.4 Newton’s second law of motion, Newton’s second law of motion states that the rate of change of momentum of a body is, directly proportional to the applied force and takes place in the direction of the force., force ∝ 𝑟𝑎𝑡𝑒 𝑜𝑓 𝑐ℎ𝑎𝑛𝑔𝑒 𝑜𝑓 𝑚𝑜𝑚𝑒𝑛𝑡𝑢𝑚, It can be easily proved that the rate of change of momentum of a moving body is equal to, the product of mass and acceleration of the body. Thus, force is proportional to the product of, mass and acceleration., State Institute of Technical Teachers’ Training & Research, , |, , Page, , 25

Page 38 :
Applied Physics - !, , 𝐹 ∝ 𝑚𝑎, 𝐹 = 𝑘 𝑚𝑎, where k is the constant of proportionality. By suitably defining the SI unit of force, we can take k, as 1. Thus,, 𝐹 = 𝑚𝑎, One unit of force is defined as that which causes an acceleration of 1m/s 2 in a body of, mass 1kg. This unit is known as newton (N)., 1 𝑁 = 1 𝑘𝑔 𝑚⁄𝑠, If ‘p’ is the momentum of the body, then Newton’s second law can be expressed in differential, form as, F=, , dp, dt, , The second law implies that if Force F = 0, then acceleration, a = 0, which means the, body is either at rest or in uniform motion. Thus, Newton’s first law can be derived from the, second law. Newton’s first law gives a qualitative idea of force and the second law gives a, mathematical expression for force., , Conceptual Learning 1.12, Consider an apple falling from a tree. The earth exerts an attractive gravitational force on the, apple due to which the apple falls towards the earth. In fact, the apple exerts the same, magnitude of the force on the earth. But the earth is not moving towards the apple. Why?, , 1.5.5 Newton’s third law of motion, Newton’s third law of motion states that to every action, there is always an equal and, opposite reaction., If a body B exerts a force, 𝐹, force,𝐹, , on a body A, then the body A exerts an equal and opposite, , on body B., , State Institute of Technical Teachers’ Training & Research, , |, , Page, , 26

Page 39 :
Applied Physics - !, , 𝐹, , = −𝐹, , Newton's third law of motion describes the nature of forces created as a result of mutual, and simultaneous interaction between two objects. The correct meaning of the third law can be, understood if the terms action and reaction are replaced by the term force. It becomes – to every, force, there is always an equal and opposite force. The main properties of action and reaction, forces are:, a) Action and reaction are the simultaneously occurring pair of forces acting between two, objects., b) Forces always occur in pairs and a single force doesn’t exist in the universe. This is an, important property of forces., c) Action and reaction are always equal in magnitude and opposite in direction. If one force, is 10N in the east direction, the other force will be 10N in the west direction., d) There is no cause-effect relation implied in the third law. Both action and reaction occur, at the same time. So, any of the two forces can be called action and the other reaction., e) The action and reaction forces, though equal and opposite, never adds up to get zero., Action and reaction do not cancel each other since they act on different objects., Examples of Newton's third law of motion are abundant in everyday life. Two examples, are cited below:, a) When a man jumps off a boat to the shore, he exerts a force on the boat. The boat exerts, an equal and opposite force on the man which makes the jump possible. The boat moves, backward due to the force exerted by the man., , Fig. 1.11 Action -reaction pair produced when a man jumps off a boat to the shore, , State Institute of Technical Teachers’ Training & Research, , |, , Page, , 27

Page 40 :
Applied Physics - !, , b) A runner exerts a force on the ground and the reaction force of the ground on the runner, pushes him forward., , Fig. 1.12 Action -reaction pair produced when a man is running, , Conceptual Learning 1.13, Identify action-reaction pairs in the following cases:, 1. A man jumping, 2. A man swimming, 3. A bird flying, 4. Striking a ball with a bat, 5. A book placed on a table, , 1.5.6 Law of conservation of momentum, From Newton’s second law of motion, the net force acting a system of particles is given, by, 𝑓𝑜𝑟𝑐𝑒 =, , change in momentum, time, , If the net force acting on the system is zero, then the change in momentum also becomes, zero. Therefore,, State Institute of Technical Teachers’ Training & Research, , |, , Page, , 28

Page 41 :
Applied Physics - !, , 𝑓𝑖𝑛𝑎𝑙 𝑚𝑜𝑚𝑒𝑛𝑡𝑢𝑚 = 𝑖𝑛𝑖𝑡𝑖𝑎𝑙 𝑚𝑜𝑚𝑒𝑛𝑡𝑢𝑚, Thus, the law of conservation of momentum states that if the net external force acting on, a system is zero, its linear momentum remains constant., As an example, we are going to prove the law of conservation of linear momentum in the, case of collision of two masses using Newton’s second law and third law. Consider two bodies, of masses 𝑚 and 𝑚 moving along a straight line with velocities 𝑢 and 𝑢 respectively. Let the, bodies collide for a time t seconds. After the collision, the velocities become 𝑣, , and, , 𝑣 respectively for masses 𝑚 and 𝑚 along the same direction as shown in Fig. 1.13., , Fig. 1.13 One dimensional collision of two masses, Since there is no external force acting on the system of two colliding bodies, the bodies, apply internal forces on each other during the collision. Let the force acting on the mass 𝑚, (applied by𝑚 ) be 𝐹 and the force acting on the mass 𝑚 (applied by𝑚 ) be 𝐹 . From, Newton’s second law of motion,, 𝑐ℎ𝑎𝑛𝑔𝑒 𝑖𝑛 𝑚𝑜𝑚𝑒𝑛𝑡𝑢𝑚, 𝑓𝑜𝑟𝑐𝑒 =, 𝑡𝑖𝑚𝑒, 𝑐ℎ𝑎𝑛𝑔𝑒 𝑖𝑛 𝑚𝑜𝑚𝑒𝑛𝑡𝑢𝑚 𝑜𝑓 𝑚, ∴ 𝐹 =, 𝑡𝑖𝑚𝑒, (𝑚 𝑣 − 𝑚 𝑢 ), 𝐹 =, 𝑡, Similarly,, (𝑚 𝑣 − 𝑚 𝑢 ), 𝐹 =, 𝑡, Since 𝐹 and 𝐹 are action-reaction pairs produced during the collision, applying Newton’s, third law of motion, we have, State Institute of Technical Teachers’ Training & Research, , |, , Page, , 29

Page 42 :
Applied Physics - !, , 𝐹 = −𝐹, (𝑚 𝑣 − 𝑚 𝑢 ), − (𝑚 𝑣 − 𝑚 𝑢 ), =, 𝑡, 𝑡, 𝑚 𝑣 − 𝑚 𝑢 = −𝑚 𝑣 + 𝑚 𝑢, 𝑚 𝑢 + 𝑚 𝑢 = 𝑚 𝑣 + 𝑚 𝑣, 𝑡𝑜𝑡𝑎𝑙 𝑚𝑜𝑚𝑒𝑛𝑡𝑎 𝑏𝑒𝑓𝑜𝑟𝑒 𝑐𝑜𝑙𝑙𝑖𝑠𝑖𝑜𝑛 = 𝑡𝑜𝑡𝑎𝑙 𝑚𝑜𝑚𝑒𝑛𝑡𝑎 𝑎𝑓𝑡𝑒𝑟 𝑐𝑜𝑙𝑙𝑖𝑠𝑖𝑜𝑛, In the case of collision of two masses, the momentum of the system is conserved, if the, external force acting on the system is zero., , Conceptual Learning 1.14, Consider an explosive lying on a surface. It explodes into (a) two pieces and (b) many pieces., Discuss the nature of the motion of the pieces in both cases., , 1.5.7 Recoil of gun, The gun carried by a soldier normally has a mass of 10 kg. On firing, the gun moves, backward such that if not handled carefully, it can hurt the person using it. The backward motion, of a gun when a bullet is fired from it is called the recoil of the gun. It can be explained using the, principle of conservation of linear momentum. The total momentum of the gun and bullet before, firing is zero. Since no external, force acts on the gun and the bullet,, its momentum should be conserved., After firing the bullet moves with a, velocity producing momentum in, the forward direction. To balance, the momentum change, the gun, moves backward with a velocity,, such that the total momentum is, zero., , Fig. 1.14 Recoil of a gun when it is fired, , State Institute of Technical Teachers’ Training & Research, , |, , Page, , 30

Page 43 :
Applied Physics - !, , Let 𝑀 and 𝑚 are masses of the gun and bullet respectively. Suppose, a bullet is fired, from the gun with a velocity 𝑣 and the gun recoils with a velocity 𝑉 ., 𝑇𝑜𝑡𝑎𝑙 𝑚𝑜𝑚𝑒𝑛𝑡𝑎 𝑏𝑒𝑓𝑜𝑟𝑒 𝑓𝑖𝑟𝑖𝑛𝑔 = 0, 𝑇𝑜𝑡𝑎𝑙 𝑚𝑜𝑚𝑒𝑛𝑡𝑎 𝑎𝑓𝑡𝑒𝑟 𝑓𝑖𝑟𝑖𝑛𝑔 = 𝑀 𝑉 + 𝑚 𝑣, , By the law of conservation of momentum, the total momenta after firing must be equal to, the total momenta before firing., 𝑀 𝑉 + 𝑚 𝑣 =0, 𝑀 𝑉 = −𝑚 𝑣, 𝑉 = −, , 𝑚 𝑣, 𝑀, , The negative sign shows that the direction recoil velocity of the gun is opposite to the, direction of the velocity of the bullet., , 1.5.8 Rocket propulsion, Rockets are used to launch artificial satellites and space shuttles, deliver explosive, warheads to their targets, and also for human space flight and scientific exploration of outer, space. The principle behind rocket propulsion is the law of conservation of momentum (external, force on rocket is zero and effect, of gravity is neglected). The, linear momentum of the rocket, including its fuel is conserved, throughout, , the, , motion., , The, , initial total momentum of the, rocket on its launching pad is, zero., , After, , the, , rocket, , is, , launched, the fuel is continuously, burned and hot gases are ejected, out in the downward direction, with high velocity. This creates a, , Fig. 1.15 Momentum of the rocket before and after, , State Institute of Technical Teachers’ Training & Research, , |, , Page, , 31

Page 44 :
Applied Physics - !, , momentum change in the downward direction. To balance it, the remaining mass of the rocket, moves in the upward direction., Newton’s third law of motion can also be used to explain the principle of rocket, propulsion. Rocket is a variable mass system because its mass decreases over time, as a result of, its fuel (propellant) burning off. As the rocket moves up, its mass decreases, and hence its, velocity increases. The velocity of the rockets can be further increased by using multistage, rockets instead of single-stage rockets. A multistage rocket has two or more rocket stages, each, stage has its engine and propellant. If one stage burns completely, it will fall off from the rocket., Hence, the mass of the rocket decreases, and its velocity increases considerably., , 1.5.9 Impulse, Consider a boy striking a ball with a bat. He hits the ball with the bat such that the force, exerted by the bat is only for a very smalltime interval. In such cases, it is difficult to measure, the force and time separately. A large force acting for a short interval of time is called an, impulsive force. We use the term impulse to measure the effect of an impulsive force on a body., Impulse (I) is defined as the product of force and time for which the force acts., 𝑖𝑚𝑝𝑢𝑙𝑠𝑒 = 𝑓𝑜𝑟𝑐𝑒 × 𝑡𝑖𝑚𝑒, 𝐼 =𝐹 ×𝑡, From Newton’s second law of motion, we have, 𝐹 = 𝑚𝑎 = 𝑚, , (𝑣 − 𝑢), 𝑡, , (𝑣 − 𝑢), ×𝑡, 𝑡, 𝐼 = 𝑚 (𝑣 − 𝑢), 𝐼 = 𝑚𝑣 − 𝑚𝑢, 𝑖𝑚𝑝𝑙𝑢𝑠𝑒 = 𝑐ℎ𝑎𝑛𝑔𝑒 𝑖𝑛 𝑚𝑜𝑚𝑒𝑛𝑡𝑢𝑚, ∴, , 𝐼= 𝑚, , Impulse is measured as the change in momentum of the body produced by the action of, impulsive force. Examples of impulsive forces are given below:, , State Institute of Technical Teachers’ Training & Research, , |, , Page, , 32

Page 45 :
Applied Physics - !, , , , Kicking a football: A footballer exerts a large force on the ball, but only for a very short, interval of time., , , , Striking a nail with a hammer: For fixing a nail, a hammer is used to exert a large force, for a small time., , , , Striking a ball with a bat: The momentary force exerted by the bat changes the direction, of the ball in a small interval., , Example 1.3, A force of 12N acts on an object of mass 6kg. Find the magnitude of the acceleration produced., Solution:, Given, , F = 12N ; m = 6kg, 𝐹 = 𝑚𝑎, , 𝑎=, , 𝐹, 12, =, = 2 𝑚⁄𝑠, 𝑚, 6, , Example 1.4, Calculate the force needed to speed up a car at the rate of 5m/s 2 if the mass of the car is 1000kg., Solution:, Given, , a = 5m/s2and, , m = 1000kg, , 𝐹 = 𝑚𝑎 = 1000 × 5 = 5000 𝑁, , Example 1.5, A mass of 5kg is initially at rest. A force of 20N is applied to it for 10 seconds. What is the, velocity at the end of 10s.?, Solution:, Given m = 5kg ;F = 20N ; u = 0 ;t = 10s, 𝐹 = 𝑚𝑎, 𝑎=, , 𝐹, 20, =, = 4 𝑚⁄𝑠, 𝑚, 5, , Using the equation𝑣 = 𝑢 + 𝑎𝑡 = 0 + 4 × 10 = 40 𝑚⁄𝑠, State Institute of Technical Teachers’ Training & Research, , |, , Page, , 33

Page 47 :
Applied Physics - !, , 𝐹 = 𝐹 − 𝐹 = 10 − 6 = 4 𝑁, 𝐹 = 𝑚𝑎, 𝑎=, , 𝐹, 4, = = 2 𝑚⁄𝑠, 𝑚, 2, , Example 1.9, A bullet of mass 40g is fired from a 5kg gun with a velocity of 250m/s. Find the recoil velocity, of the gun., Solution:, , Given, , 𝑚 = 40 𝑔 = 40 × 10, , 𝑘𝑔 ;𝑣 = 250 𝑚⁄𝑠 ; 𝑀 = 5 𝑘𝑔 ;, , Recoil velocity of the gun is given by, 𝑉 =−, , 𝑚 𝑣, 40 × 10 × 250, = −, = −2 𝑚⁄𝑠, 𝑀, 5, , PRACTICE PROBLEMS, 1. The readings of an experiment involving measurement of time give 2.78s, 2.90s, 2.92s, and, 2.85s. Find the absolute error, relative error, and percentage error., 2. Find the percentage error for the following measured values – 23.5,24.4, 23.9,23.0, and 24.3., 3. A force of 20N acts on a body of mass 4kg. Find the acceleration produced., 4. A body at rest is acted upon by a force so that it reaches a velocity of 20m/s in 4s.If the mass, of the body is 3kg, find the force., 5. A car of mass 1000kg moving at 20m/s is brought to rest over a distance of 40m.Find the, braking force., 6. An object is moving at 40m/s. A force of 10N is applied opposite to its direction of motion., Find the time taken by the object to come to rest., 7. The momentum of a body changes from 40kgm/s to 10kgm/s in 5s in the same direction by, the application of a force. Find the force applied., 8. A body of mass 1kg is acted upon by two perpendicular forces 3N and 4N.Find the, magnitude of the acceleration of the body., State Institute of Technical Teachers’ Training & Research, , |, , Page, , 35

Page 48 :
Applied Physics - !, , 9. A gun of mass 8kg fires a bullet of mass 80g with a velocity of 300m/s. Find the recoil, velocity of the gun., 10. A shell of mass 0.02kg is fired from a gun of mass 200kg with a velocity of 100m/s. Find the, recoil velocity of the gun., , QUESTIONS, 1. Define the unit of a physical quantity., 2. Differentiate between fundamental quantity and derived quantity., 3. What are the seven fundamental quantities and their units in the SI system?, 4. Explain different types of errors in measurements., 5. Distinguish between absolute error, relative error, and percentage error., 6. State and explain the triangular law of vector addition., 7. State and explain the parallelogram law of vector addition., 8. Explain the term resolution of a vector., 9. State Newton’s first law of motion and explain inertia, 10. Define force from the first law of motion., 11. State and explain Newton’s second law of motion., 12. With the help of an example explain Newton’s third law of motion., 13. Explain the recoil of a gun. Derive an expression for the recoil velocity of the gun., 14. Explain the propulsion of a rocket using the law of conservation of momentum., 15. What is impulse? Show that change impulse is equal to change in momentum., , State Institute of Technical Teachers’ Training & Research, , |, , Page, , 36

Page 49 :
Applied Physics - !, , CHAPTER 2, ROTATIONAL MOTION, , Conceptual Learning 2.1, Classify the motion of bodies given below into different categories., 1. A train moving on a straight rail track, 2. A spinning wheel, 3. The earth revolving around the sun, 4. Swinging of pendulum, 5. The motion of the string of a guitar, , 2.1 BASIC TYPES OF MOTION, Everything in the universe is moving and evolving. There are basically four different, types of motion namely translational motion, rotational motion, oscillatory motion, and random, motion., a) Translational motion, Translational motion is a motion in which the location of the object changes with time., Translational motion can again be classified into two types – rectilinear motion and curvilinear, motion. In rectilinear motion, the object moves along a straight line whereas, in curvilinear, motion, the object moves along a curved path. Circular motion is a special type of curvilinear, motion in which an object moves along a circular path. In translational motion, all objects are, considered as point masses., State Institute of Technical Teachers’ Training & Research, , |, , Page, , 37

Page 50 :
Applied Physics - !, , Examples:, , The motion of elevators in buildings (rectilinear motion), The motion of a basketball into the basket (curvilinear motion), The motion of satellites around the earth (circular motion)., , b) Rotational motion, Rotational motion is a motion in which the objects spin around an axis and the location of, the object do not change with time. Rotational motion is always associated with rigid extended, bodies. During rotational motion, each particle constituting the rigid body undergoes circular, motion. Hence circular motion and rotational motion are closely related., Example: Motion of blades of the ceiling fan, c), , Oscillatory motion, Oscillatory motion is the to and fro motion of an object about a fixed point. It is a special, , type of periodic motion – a motion that repeats itself in a regular interval of time., Example: Oscillations of a pendulum, d) Random motion, Random motion is a motion in which the particle moves in a zig-zag manner and the, direction of motion changes continuously. This kind of motion is unpredictable in practice., Example: Motion of honey bee, , Conceptual Learning 2.2, 1. Find out at least two examples for each type of motion., 2. What are the different types of motion associated with different parts of a bicycle in motion?, , 2.2 CIRCULAR MOTION, The motion of a body along the circumference of a circle is called circular motion. In a, circular motion, the direction of motion changes continuously. When a particle moves uniformly, along a circle, the direction of its velocity changes constantly, but its magnitude remains, constant. A circular motion is said to be uniform when a particle moves along a circular path, State Institute of Technical Teachers’ Training & Research, , |, , Page, , 38

Page 51 :
Applied Physics - !, , with a constant speed. The following parameters are required for the understanding of circular, motion., , 2.2.1 Angular displacement (θ), Consider a particle moving, along the circumference of a circle of, radius r with centre O. When the, body moves from A to B in time t, seconds and covers a distance s,, angular displacement, θis the angle, subtended at centre O., , 𝜃=, , 𝑠, 𝑟, , Fig. 2.1 Angular displacement in circular, , The angle described by a body moving along a circular path in a given time is known as, angular displacement. The SI unit of angular displacement is radian., Angular displacement can be expressed in degrees or radians or revolutions. One, revolution corresponds to 360 0or 2π radians., , = 57.30, , 1 radian =, , 2.2.2 Linear velocity (v), The distance travelled by a body moving along a circular path in unit time is called its, linear velocity. Let v be the linear velocity of the particle and s be the linear displacement in time, t seconds., Linear velocity =, 𝑣=, , s, t, , The unit of linear velocity is m/s., , 2.2.3 Angular velocity (𝝎), The angular displacement per unit time is called angular velocity. It is denoted by the, symbol 𝜔. The SI unit of angular velocity is radian/second (rad/s)., State Institute of Technical Teachers’ Training & Research, , |, , Page, , 39

Page 52 :
Applied Physics - !, , Angular velocity =, 𝜔=, , 2.2.4 Linear acceleration (a), Linear acceleration is the rate of change of linear velocity of a body moving along a, circular path or it is the change in linear velocity of a body in unit time. If the linear velocity of a, body changes from 𝑣 to 𝑣 in t seconds,, Linear acceleration, a, , =, , The unit of linear acceleration is m/s2., , 2.2.5 Angular acceleration (α), Angular acceleration is the rate of change of angular velocity. If the angular velocity of a, body changes from 𝜔 to 𝜔 in t seconds, the angular acceleration α is given by, α=, The unit of angular acceleration is rad/𝑠 ., , 2.2.6 Relation between linear velocity and angular velocity, Consider a particle moving along the circumference of a circle of radius r with a linear, velocity v. When the body moves from A to B in time t seconds and covers a distance, s, the, angular displacement, θ is given by, 𝑠, 𝜃=, 𝑟, 𝑠 = 𝑟𝜃, The linear velocity of the particle is given by, , 𝑣=, , 𝑠, 𝑟𝜃, =, 𝑡, 𝑡, , Since angular velocity, 𝜔 = ,, 𝑣 = 𝑟𝜔, , State Institute of Technical Teachers’ Training & Research, , |, , Page, , 40

Page 53 :
Applied Physics - !, , 2.2.7 Relation between linear acceleration and angular acceleration, Consider a particle moving along the circumference of a circle of radius r. If the linear, velocity of a body changes from 𝑣 to 𝑣 in t seconds,, Linear acceleration, 𝑎 =, If the angular velocity of the body changes from 𝜔 to 𝜔 during the time t seconds, then from, the relation between linear velocity and angular velocity,, 𝑣, 𝑟𝜔, 𝑣, ∴, , ∴, , Since angular acceleration,, , 𝛼=, , (, , 𝑎=, , 𝑎=, , ), , 𝑟𝜔, 𝑟𝜔 − 𝑟𝜔, 𝑡, 𝑟 (𝜔 − 𝜔 ), 𝑡, , ,, 𝑎=𝑟𝛼, , The relations between various linear quantities and angular quantities can be summarized in, table 2.1., Table 2.1 Relation between linear and angular quantities, linear quantity = radius x angular quantity, displacement = radius x angular displacement, velocity = radius x angular velocity, , s = r, v = rω, , acceleration = radius x angular acceleration, , a=rα, , 2.2.8 Period (T), The time required to complete one revolution is called period(T). When one revolution is, completed, angular displacement is of 2π radians. Then angular velocity is given by, State Institute of Technical Teachers’ Training & Research, , |, , Page, , 41

Page 54 :
Applied Physics - !, , ∴, , 𝜔=, , 2π, 𝑇, , 𝑇=, , 2π, 𝜔, , Conceptual Learning 2.3, Compare the angular velocity of the hour hand of a watch and the angular velocity of the, earth’s rotation., , Example 2.1., A stone at the end of a string 0.5m long makes 12 revolutions in 3 seconds. Find (1) angular, velocity (2) linear velocity (3) distance travelled in 5 seconds., Solution:, Since the body makes 12 revolutions in 3 seconds, T =, (1) Angular velocity, ω =, , =, , × ., , = 0.25 s, , = 25.12 rad/s, , ., , (2) Linear velocity, v = r𝜔 = 0.5 x 25.12 = 12.56m/s, (3) Distance travelled in 5 seconds, 𝑠 = 𝑣𝑡 = 12.56 × 5 = 62.8m, Example 2.2, Determine the angular acceleration of a wheel that starts from rest and attains a speed of 600 rpm, in one minute., Solution:, Initial angular velocity, ω1 = 0, Final angular velocity, ω2 =, Angular acceleration,α =, , =, , × ., , = 62.8 rad/s, , ., ., , =, , State Institute of Technical Teachers’ Training & Research, , |, , = 1.046 rad/s2, , Page, , 42

Page 55 :
Applied Physics - !, , Example 2.3, The angular velocity of a particle moving along the circumference of a circle changes from 30 to, 60 revolutions per second within 20 seconds. If the radius of the circle is 2m, calculate its linear, acceleration and angular acceleration., Solution:, Radius,r = 2m, Initial period,T1 =, , = 0.033s, , Period after 20 seconds,T2 = =, Initial angular velocity, ω1 =, , = 0.0166s, =190.30 rad/s, , Angular velocity after 20 seconds,ω2 =, Angular acceleration, α =, , = 378.31 rad/s, , = 9.4rad/ s2, , Linear acceleration, a = r α = 2 x 9.4 =18.8 m/s 2., , 2.2.9 Centripetal acceleration (ac), A cyclist while going around a curve on a horizontal track has to bend himself a little from his, vertical position to avoid overturning. We, know something must be “pulling” the, cycle from its straight-line tendency into a, circular path. What happens if the cyclist, increases the speed of the cycle?, If a particle moves along the, circumference of a circle with constant, speed,, , its, , direction, , changes, , continuously. A force is necessary to, change the direction of the body. This, force keeps the body in a circular path, by continuously changing its direction, , Fig. 2.1 Centripetal acceleration in circular motion, , and the particle undergoes acceleration., The acceleration of a particle moving along a circular path with uniform speed is always, directed towards the centre of the circle. This acceleration is called centripetal acceleration. The, State Institute of Technical Teachers’ Training & Research, , |, , Page, , 43

Page 56 :
Applied Physics - !, , word centripetal means ‘directed towards the centre’. If v is the speed and r the radius of the, circle, the centripetal acceleration is given by, 𝑎 =, , 𝑣, 𝑟, , 2.2.10 Centripetal force (Fc), The force which, acting along the, radius towards the centre of the circular path,, causes the body to move in a circle with, constant speed is called centripetal force. If m, is the mass of the body moving along a circle of, radius r, centripetal force, 𝑚𝑣, 𝐹 =, 𝑟, Fig. 2.3 Centripetal force in circular, motion, Centripetal force is used to refer to the force experienced by an object traveling along a, circular path. For example, if a body is attached at one end of a string and whirled round, the, string transmits a centripetal force from the muscles of the hand and arm, causing the ball to, move in a circular path. The centripetal force causes centripetal accelerations. In the case of the, Earth's circular motion around the Sun, the centripetal force causing the motion is the result of, the gravitational attraction between them., Centripetal force must be continuously supplied to keep a body moving along a circular, path with uniform velocity. The centripetal force is provided differently for different bodies and, a few examples are given below:, a) If a body is attached at one end of a string and whirled round, the tension provides the, centripetal force., b) In the case of planets revolving around the sun, the necessary centripetal force is, provided by the gravitational attraction between them., c) When an electron moves around the nucleus of an atom, the centripetal force is provided, by the electrostatic force of attraction between electron and proton., State Institute of Technical Teachers’ Training & Research, , |, , Page, , 44

Page 57 :
Applied Physics - !, , d) When a vehicle moves along a curved path, the centripetal force is provided by the, frictional force between the tyres and the road., , Conceptual Learning 2.4, Find out three real-life examples of centripetal force., , 2.2.11 Banking of roads, When a vehicle goes around a curve, it travels along a nearly circular path. Centripetal, force is required to keep an object in a circular path. In a horizontal unbanked curve, the weight, of the vehicle is balanced by the normal reaction whereas the necessary centripetal force is, provided by the friction between the wheels (tyres) and the surface of the road. If the friction is, inadequate, the vehicle skid off the road. To avoid skidding, the outer edge of the road is raised, above the level of the inner edge at the curves. This is known as the banking of roads. The, banking of roads avoids skidding and reduces wear and tear of the tyres. In a banked road, the, horizontal component of normal reaction will also contribute to centripetal force in addition to, frictional force., , Fig. 2.4, , (a) Centripetal force for circular motion of a car in a horizontal curve, (b) Centripetal force for circular motion of a car in a banked curve, , State Institute of Technical Teachers’ Training & Research, , |, , Page, , 45

Page 58 :
Applied Physics - !, , 2.2.12 Expression for the angle of banking (θ), The angle of banking is the angle made by the elevated path with the horizontal.Let AB, and AC represent the horizontal and banked paths respectively as shown in Fig 2.4 (b). Let θ be, the angle of banking. Consider a vehicle of mass m takes a curved path of radius r with a speed, v. The weight of the vehicle mg acts vertically downwards. The normal reaction N of the road on, the vehicle will be perpendicular to the AC. The normal reaction can be resolved into vertical, and horizontal components., The vertical componentis equal to the weight of the body., 𝑁𝑐𝑜𝑠𝜃 = 𝑚𝑔, The horizontal component provides the centripetal force, 𝑚𝑣, 𝑁𝑠𝑖𝑛𝜃 =, 𝑟, Dividing the second equation by the first gives, 𝑣, 𝑡𝑎𝑛𝜃 =, 𝑟𝑔, , 𝜃 = 𝑡𝑎𝑛, , 𝑣, 𝑟𝑔, , The angle of banking depends on the radius of the curve of the road and the speed of the vehicle., , 2.2.13 Banking of railway tracks, In the case of a train moving through a curved track, centripetal force is required towards, the centre of the circular track. This force is provided by the thrust exerted by the side of the, outer rail against the flange of the outer wheel. When a fast-moving train takes a curved path, it, tends to move away tangentially off the track. To avoid this, the outer rail is raised above the, level of the inner rail. This is known as the banking of railway tracks. The banking of railway, tracks avoids skidding and reduces the wear and tear of the wheels., In the case of a curved railway track, the level of the outer rail is higher than that of the, inner one. The height of the outer rail above the inner rail in the banked rail track is called, , State Institute of Technical Teachers’ Training & Research, , |, , Page, , 46

Page 60 :
Applied Physics - !, , Example 2.4, A mass of 10 kg at the end of a string is being whirled in a circle of radius 2m with a constant, speed of 5m/s. Find (1) centripetal acceleration (2) centripetal force., Solution:, (1) Centripetal acceleration, a =, (2) Centripetal force, F =, , 𝒗𝟐, 𝒓, , =, , 𝟓𝟐, 𝟐, , =, , = 12.5 m/s2, , = 125 N, , Example 2.5, What is the angle of banking for a curved track of radius 100m suitable for a maximum speed of, 72km/hr?, Solution:, Radius of the curve, r = 100m, Speed, v =, , ×, , = 20 m/s, , Since θ be the angle of banking, , =, , tan𝜃 =, 𝜃= tan-1(, , × ., , = 0.4081, , )= tan-1(0.4081) = 22.20, , Example 2.6, A train is moving with a speed of 36km/hr on a curved path of radius, 100 m. If the distance, between the rails is 1.5m, find the height of the outer rail over the inner rail., Solution:, Speed of the train, v =, , ×, , = 10 m/s, , Radius of the path, r =100m, Distance between the rails, d =1.5 m, S=, , =, , × ., × ., , = 0.153m, , State Institute of Technical Teachers’ Training & Research, , |, , Page, , 48

Page 61 :
Applied Physics - !, , 2.3 ROTATIONAL MOTION OF RIGID BODIES, A rigid body is a body that does not change its size or shape under the action of external, forces. When an external force acts on a rigid body, the distance between the two points on the, body does not change. In reality, no body is a rigid body and there will be some forces under, which the body will change its shape. For example, a bridge will not change its shape under the, weight of a single person, it might change shape under the weight of a truck, even though the, change will be small. The motion of a rigid body in which all particles of the body move in a, circular path about a fixed-line with common angular velocity is called rotational motion. The, fixed line about which rotation takes place is called the rotational axis. The linear velocity of, each particle of the rigid body will be different since particles are located at a different distance, from the axis of rotation., Examples: Rotation of Earth, A top spinning about its axis, Rotation of a fan, , Conceptual Learning 2.6, Find out three real-life examples of rotational motion., , 2.3.1 Moment of inertia (Rotational inertia), According to Newton’s first law, an object at rest tends to stay at rest and an object in, motion tends to remain in motion. Just like that, an object rotating about an axis tends to remain, rotating about the same axis while a non-rotating object tends to remain non-rotating. The, property of an object to resist any change in its state of rotational motion is called rotational, inertia or moment of inertia. When a body is rotating about a fixed axis, the opposition to its, motion depends on the mass and distribution of mass about the axis of rotation (shape of the, body). The greater the moment of inertia of the object, the harder it is to change the rotational, state of that object., The moment of inertia is the measure of an object’s resistance to change its direction of, rotation. It is a parameter of how difficult it is to change the rotational velocity of an object, about a particular rotational axis. The moment of inertia depends not only on the mass of the, object but also on how that mass is distributed relative to the rotational axis. The moment of, State Institute of Technical Teachers’ Training & Research, , |, , Page, , 49

Page 62 :
Applied Physics - !, , inertia of a system tends to be bigger if more mass is located farther away from the rotational, axis. This means that it becomes more difficult to alter the rotational velocity of a system if the, object is kept far away from the center of the axis., , 2.3.2 Moment of inertia of a particle, The moment of inertia of a particle about, a given axis is defined as the product of the mass, of the particle and the square of the distance of, the body from the axis., Consider a particle of mass m capable of, rotation about an axis AB. Let r be the, perpendicular distance of the particle from AB., The moment of inertia about the axis AB, I = mr2, The SI unit of moment of inertia is kgm2. The, moment of inertia of a body depends on, , Fig. 2.6Moment of inertia of a particle, , 1. Mass of the body., 2. The distribution of mass with respect to the axis of rotation., , Conceptual Learning 2.7, Consider a ring and a circular disc of the same mass and radius rotating about an axis passing, through its centre and perpendicular to its plane. Which has more moment of inertia?, , 2.3.3 Moment of inertia of a rigid body, Consider a rigid body capable of rotation, about an axis AB. Let us consider particles of, masses m1, m2, m3,etc. of the body at distances r1,, r2, r3,etc. respectively from the axis AB. The, moment of inertia is the sum of the Moment of, State Institute of Technical Teachers’ Training & Research, , Fig. 2.7Moment of inertia of a rigid body, |, , Page, , 50

Page 63 :
Applied Physics - !, , inertia of the individual particles of the body about the axis of rotation., Moment of inertia of m1 about AB = m1r12, Moment of inertia of m2 about AB = m2r22, Moment of inertia of m3 about AB = m3r32, ……………………………………………., Moment of inertia of mn about AB = mnrn2, Therefore, the total moment of inertia of the body about the axis of rotation AB,, I = m1r12 + m2r22 + m3r32+ ……mnrn2, I=∑, , 𝑚 𝑟, , 2.3.4 Radius of gyration(K), Consider a rigid body of mass M and moment of inertia I about the given axis as shown, in the figure. We can assume that the entire mass of the body is concentrated at a point and this, point is placed at a distance K from the axis of rotation with the condition that the moment of, inertia of the point mass will be equal to the moment of inertia of the rigid body. This imaginary, distance K is called the radius of gyration. The radius of gyration (K) is the distance from the, axis of rotation to the point at which the entire mass of the body is assumed to be concentrated so, that the moment of inertia will be equal to the moment of inertia of the actual body.The radius of, gyration is of a body about an axis of rotation represents the effective distance of the particles of, the body from the axis of rotation., , Fig. 2.8 Radius of gyration of a rigid body about the given axis, State Institute of Technical Teachers’ Training & Research, , |, , Page, , 51

Page 64 :
Applied Physics - !, , If M is the total mass of the body and K is the radius of gyration of the body about the axis of, rotation, then the moment of inertia is given by, I = MK2, , 𝐾=, , 𝐼, 𝑀, , The SI unit of the radius of gyration is meter. The radius of gyration depends on, 1. The distribution of mass from the axis of rotation., 2. The position and direction of the axis of rotation., , 2.3.5 Theorems on Moment of Inertia, a) Parallel axes theorem, Parallel axes theorem states that the, moment of inertia of any rigid body about a, given axis is equal to the sum of its moment, of inertia about a parallel axis passing, through the centre of gravity and the, product of the mass of the body and the, square of the distance between the axes., Let I be the moment of inertia of a, body about an axis AB. Let IG be the, moment of inertia about another axis CD, , Fig. 2.9 Parallel axes theorem for a rigid, body, the centre of gravity G of the body. Let M be the mass and a be the distance between the two, which is parallel to AB and passing through, , axes. Then according to the parallel axes theorem,, , I = IG + Ma2, State Institute of Technical Teachers’ Training & Research, , |, , Page, , 52

Page 65 :
Applied Physics - !, , b) Perpendicular axes theorem, Perpendicular axes theorem states that the sum of the moments of inertia of a plane, lamina about two mutually perpendicular axes in its plane is equal to its moment of inertia about, a perpendicular axis passing through the intersection of the first two axes., Let OX and OY be two mutually, perpendicular axes in the plane of the, lamina intersecting each other at point O., The axis OZ is perpendicular to both OX, and OY. If IX, IY, and IZ are the moment of, inertia about the axes OX, OY, and OZ, respectively, then by perpendicular axes, theorem, , I X + I Y = IZ, , Fig. 2.10 Parallel axes theorem for a plane, lamina, , 2.3.6 Moment of inertia of continuous mass distributions, If the body is continuous, its moment of inertia about a given axis can be obtained using, the technique of integration. Consider a small element of the body of mass dm at perpendicular, distance r from the axis of rotation. The, moment of inertia of the element about, the given axis is, 𝑑𝐼 = 𝑟 𝑑𝑚, The moment of inertia of the rigid body, about the given axis is obtained by, integrating the above equation over, appropriate limits to cover the whole, body. Thus,, 𝐼=, , 𝑟 𝑑𝑚, , Fig. 2.11 Moment of inertia of a continuous body, , State Institute of Technical Teachers’ Training & Research, , |, , Page, , 53

Page 66 :
Applied Physics - !, , Fig. 2.12 Moment of inertia of (a) a thin road (b) a ring (c) a circular disc, (d) solid sphere and (e) hollow sphere about the given axis, , a) Moment of inertia of a thin uniform rod, about an axis through its centre and, perpendicular to its length., Consider a thin uniform rod of length l and mass M as shown in Fig. 2.12 (a).Its moment of, inertia about an axis through its centre and perpendicular to its length is given by, 1, 𝐼=, 𝑀𝑙, 12, b) Moment of inertia of a ring, about an axis through the centre and perpendicular to its, plane., Consider a circular ring of radius R and mass M as shown in Fig. 2.12 (b). Its moment of, inertia about an axis through the centre and perpendicular to its plane is given by, 𝐼 = 𝑀𝑅, , State Institute of Technical Teachers’ Training & Research, , |, , Page, , 54

Page 67 :
Applied Physics - !, , c) Moment of inertia of a thin uniform circular disc, about an axis through the centre and, perpendicular to its plane., Consider a uniform circular disc of radius R and mass M as shown in Fig. 2.12 (c).Its, moment of inertia about an axis through the centre and perpendicular to its plane is given by, 𝐼=, , 1, 𝑀𝑅, 2, , d) Moment of inertia of a solid sphere, about any diameter., Consider a solid sphere of radius R and mass M as shown in Fig. 2.12 (d). Its moment of, inertia about any diameter is given by, 𝐼=, , 2, 𝑀𝑅, 5, , e) Moment of inertia of a hollow sphere, about any diameter., Consider a hollow sphere of radius R and mass M. Its moment of inertia about any diameter, is given by, 𝐼=, , 2, 𝑀𝑅, 3, , Conceptual Learning 2.8, We know that the moment of inertia of a circular disc about a perpendicular axis through its, centre is, , 𝑀𝑅 where M is mass and R is the radius of the disc. Find out the moment of inertia, , of the disc (i) about a diameter of the disc and (ii) about a tangent in the plane of the disc by, applying parallel axes theorem or perpendicular axes theorem., , 2.3.7 Torque(τ), Hold a meter scale horizontally in your hand., Hang a weight on the scale. Slide the weight to the, other end. Your hand will experience a twist., Farther the weight from the hand larger the twist, experienced. The twist experienced on the hand is, Fig. 2.13 Weight hanging on a scale, , known as torque., Anyone who has ever opened a door has an, State Institute of Technical Teachers’ Training & Research, , |, , Page, , 55

Page 68 :
Applied Physics - !, , understanding of torque. We know that door opens slowly if we push too close to its hinges. We, can easily open a door if force is applied at a point that is farthest from the hinges. Furthermore,, we know that the more massive the door, the more slowly it opens., In the case of linear motion, force is required to produce linear acceleration to a body., Similarly in rotational motion torque is required to produce angular acceleration. Force tends to, change the motion of things. Torque tends to twist or change the state of rotation of things. Force, should be applied to move a stationary object while torque is applied to rotate a stationary object., Hence, torque is the rotating effect of the force on a body., Consider a rigid body that is free to, rotate about an axis. A force is applied to the, rigid body at a perpendicular distance r from, the axis of rotation as shown in the figure. The, rotating effect of force on the rigid body about, the axis of rotation depends on the magnitude, of the force applied and the perpendicular, distance of the point of application of the force, from the axis of rotation., Torque is defined as the product of the, force and the perpendicular distance between, , Fig. 2.14 Torque acting on a rigid body, , the line of action of the force and the axis of, rotation., , 𝜏 = 𝐹𝑟, The SI unit of torque is newton meter (Nm)., Torque also depends on the angle between the force and the line joining the point of, application of the force and the axis of rotation. If the angle between r and F is θ, the, perpendicular distance between the line of action of the force and axis of rotation becomes, 𝑟𝑠𝑖𝑛𝜃. Therefore,, 𝜏 = 𝐹𝑟𝑠𝑖𝑛𝜃, State Institute of Technical Teachers’ Training & Research, , |, , Page, , 56

Page 69 :
Applied Physics - !, , The torque is maximum when θ = 90o or 𝑠𝑖𝑛𝜃 = 1and 𝜏, Torque is minimum when θ = 0o or 𝑠𝑖𝑛𝜃 = 0 and 𝜏, , = 𝐹𝑟., , = 0., , Torque is the rotational equivalent of force. We can relate the torque on a rigid body to, the angular acceleration., 𝜏 = 𝐹𝑟, From Newton’s second law of motion,, 𝐹 = 𝑚𝑎, ∴, , 𝜏 = 𝑚𝑎𝑟, , The relation between linear acceleration and angular acceleration is given by, 𝑎 = 𝑟𝛼, ∴, , 𝜏 = 𝑚 𝑟𝛼𝑟, 𝜏 = 𝑚𝑟 𝛼, , Since the moment of inertia, 𝐼 = 𝑚𝑟, 𝜏 = 𝐼𝛼, , Conceptual Learning 2.9, Evaluate the statement and give an explanation based on the concept of torque, 1. If the force is applied parallel to the surface of the door, it will not open., 2. If the force is applied perpendicular to the plane of the door it will open., 3. To unscrew a nut using a spanner, the force is applied at the other end of the spanner., 4. A wheel capable of rotation about its axis can rotate easily if a force is applied at the, , rim rather than at a point near the axis of rotation., , 2.3.8 Angular momentum (L), The angular momentum of a rotating, body is the product of the moment of inertia, about the axis of rotation and the angular, velocity., 𝐿 = 𝐼𝜔, , Fig. 2.15 Angular momentum of a rigid body, , State Institute of Technical Teachers’ Training & Research, , |, , Page, , 57

Page 70 :
Applied Physics - !, , The angular momentum of a rotating body plays the same role as the momentum in linear, motion. The SI unit of angular momentum is Js or kg m 2 s-1, , 2.3.9 Conservation of angular momentum, The principle of conservation of angular momentum states that, if no external torque acts, on a system, the total angular momentum of the system remains constant. The angular, momentum of the system will be conserved if the net external torque on the system is zero. If I, be the moment of inertia of a body about a given axis of rotation and ω be its angular velocity,, then L = I ω = constant., , Fig. 2.16 Man holding weights standing on a turntable, When a man with outstretched arms and holding weights in each hand, stands on a turntable, that is revolving, he has certain angular momentum. If he pulls the weights in towards his body,, suddenly the angular velocity increases. This happens because when he pulls the weight inwards, the, moment of inertia of the man decreases., Conservation of angular momentum demands that the decrease in moment of inertia must be, accompanied by an increase in angular velocity so that the angular momentum remains constant. For a, rigid body, the moment of inertia and angular velocity remains constant during the motion. If the, moment of inertia changes from I1 to I2, then in the absence of external torque, the angular velocity of, the body changes from ω1toω2.This can be mathematically written as I1ω1 = I2ω2, if τ = 0., , State Institute of Technical Teachers’ Training & Research, , |, , Page, , 58

Page 71 :
Applied Physics - !, , Conceptual Learning 2.10, 1. If the ice on the polar caps of the earth melts, how will it affect the duration of the day?, 2. If the earth were suddenly shrunk to half of its radius, what happens to the duration of the, day?, 3., , When a diver jumps into water from a height, he does not keep his body straight but pulls, in his arms and legs towards the centre of the body. Why?, , Table 1.2Comparison between linear motion and rotational motion, Linear motion, , Rotational motion, , Linear displacement(s), , Angular displacement(θ), , Linear velocity(v), , Angular velocity (ω), , Linear acceleration (a), , Angular acceleration(α), , Mass(m), , Moment of inertia(I) [I = mr2], , Linear momentum(p), , [p = mv], , Angular momentum(L) [ L = I ω], , Force(F), , [F = ma], , Torque(τ), , State Institute of Technical Teachers’ Training & Research, , |, , [ τ = Iα], , Page, , 59

Page 72 :
Applied Physics - !, , PRACTICE PROBLEMS, 1. Calculate the angular velocity of the second hand of a watch. [0.104 rad/s], 2. A stone of mass 5 kg is tied to a string 2m long and whirled in a horizontal circle making, 60 revolutions per minute. Find the tension in the string.[ Ans: 394.3 N], 3. To what angle must a circular track of radius of curvature 250m be banked to be suitable, for a maximum speed of 90 km/hr.[ Ans:14.300], 4. A car is racing on a circular track of 100 m radius and banking angle 30 0. To avoid, skidding, what should be the speed of the car? [ Ans: 23.77 m/s], 5. Find the centripetal force required to revolve a body of mass 4.9 kg along a circular path, of radius 1m and making 300 revolutions per minute.[ Ans: 4831.2], 6. A train is moving with a speed of 36 km/hr on a curved path of radius, 200m., If the distance between the rails is 1.5m, find the height of the outer rail over the inner rail., [Ans:0.076m], , QUESTIONS, 1. A bar that has weights attached to its ends is more difficult to rotate than one with weights, attached close to the centre of the bar. Why?, 2. Why do tightrope walkers carry a long pole?, 3. Door handles are usually fitted at the edge of the plank of the door. Why?, 4. Given a hard-boiled egg and a raw egg, how will you differentiate between them by, spinning on a tabletop?, 5. Explain the term banking of roads. Derive an expression for the angle of banking., 6. Define the moment of inertia of a body., 7. State and explain parallel axes theorem., 8. A solid cylinder and hollow cylinder having the same mass and the same diameter are, released simultaneously from the top of an inclined plane. Which will reach the bottom, first? Explain., 9. What furnishes the required centripetal force in each of the following:, a), , the earth revolving around the sun, , b), , a car negotiating a curve, , c), , an electron revolving around the nucleus., , 10. Derive the relation between linear velocity and angular velocity of a body moving, in a circular path., 11. Define the term torque., 12. State the law of conservation of angular momentum., State Institute of Technical Teachers’ Training & Research, , |, , Page, , 60

Page 73 :
Applied Physics - !, , CHAPTER 3, WORK, ENERGY, AND POWER, 3.1 WORK, In everyday life, any physical or mental activity may be regarded as ’work’., , For, , example, a teacher taking a class is doing work or students learning while sitting on the benches, are doing work. However, all such activities do not fall under the category of work. In Physics,, work is said to be done only when the applied force causes some displacement of a body in its, direction., , Conceptual Learning 3.1, , Consider a body of mass M1 pushed from position A to position B through a distance x., Let a force F is required to move the body M1 through distance x, and work done by the, force is taken as W., , Now imagine another body of mass M2, which is heavier than M1, pushed from position, A to B., 1. Evaluate the following statements:, a) The force required to move M2 through a distance x is F, b) Work required to move M2 through a distance x is W, 2. What about force and work if M1 moved from A to C through a distance of 2x?, , State Institute of Technical Teachers’ Training & Research, , |, , Page, , 61

Page 74 :
Applied Physics - !, , 3.1.1 Work in Physics, We can say that the work done by a body depends upon the force applied as well as the, displacement of a body. Force applied on the body increases; the work done also increases. If a, constant force is applied to a body in different directions, the work done depends on the, displacement of the body in the direction of the force. Hence, Work in Physics is defined as the, product of force and displacement in the direction of the force. If F is the applied force, S is the, displacement in the direction of applied force, and work done W is given by, Work done = Force x Displacement in the direction of force, 𝑊 =𝐹×𝑆, Work is a scalar quantity. In the SI system, the unit of work is Nm or joule (J)., 1 J = 1 N x 1 m = 1 kg m/s2 x 1m = 1 kgm2s-2, , Conceptual Learning 3.2, If you push a wall, it does not displace from its position whereas if you push a table, it gets, displaced. If the force applied in both cases is the same, find out the difference between the two, cases in the context of work done., , 3.1.2 Types of work, a) Positive work, The work done on an object is said to be positive work when force and displacement are, in the same direction. Work done by the gravitational force on a freely falling body is an, example of positive work., b) Negative work, The work done is said to be negative work when force and displacement are in opposite, directions. When a body is thrown upwards, the work done by the gravitational force and, displacement are opposite and hence, it is an example of negative work., , State Institute of Technical Teachers’ Training & Research, , |, , Page, , 62

Page 75 :
Applied Physics - !, , c)Zero work, The work done is said to be zero when force and displacement are perpendicular to each, other or when either force or displacement is zero. Work done by gravity when a person walks, horizontally with some load on his head is an example of zero work., , Conceptual Learning 3.3, Find out more examples of positive, negative, and zero work., , 3.2 ENERGY, All living beings perform certain basic activities in order to survive. For performing these, activities, they need energy, which comes from the food which they consume. The word energy, is commonly used in our daily life. Science has given it a definite and precise meaning. Let us, consider few examples:, 1. When a raised hammer hits a nail placed on a piece of wood, it drives the nail into the wood., 2. When the striker hits the stationary carom coin, it sets the carom coin into motion., In the above examples, a hammer or striker has the capacity to do work on another object., The object which does work loses energy. At the same time, the object on which work is done, gains energy. The capacity (or ability) of a body to do work is called energy. Energy and work, are equivalent concepts. The SI unit of energy is also joule (J)., , 3.2.1 Types of Energy, Energy can exist in many forms, but it can be broadly classified into two categories –, kinetic energy and potential energy., , State Institute of Technical Teachers’ Training & Research, , |, , Page, , 63

Page 76 :
Applied Physics - !, , a) Kinetic Energy, The energy possessed by a body due to its motion is called kinetic energy. A moving, vehicle, Earth revolving around the sun, and molecules moving in space all have kinetic energy., The kinetic energy of a moving object is directly proportional to the mass of the object and the, square of its velocity. If m is the mass of the body and v is its velocity, then kinetic energy is, given by, 𝐾=, , 1, 𝑚𝑣, 2, , b) Potential Energy, The energy possessed by a body by its position or configuration is called potential, energy. For example, if we carry a brick to the top of the building, we do some amount of work, against the force of gravity. The amount of energy is stored in the brick, in the form of potential, energy. Consider a bow and arrow. Pull the string along with the arrow in the backward direction, by applying force. In doing so you change the configuration (shape) of the bow. The energy is, used up in changing the shape of the bow and it is stored in the bow in the form of potential, energy. Water stored in a tank, a stretched rubber chord, etc. have potential energy., The potential energy of a body depends on the type of force acting on the body. Consider, a mass m held at a height h above ground level in the gravitational field of Earth. If g is the, acceleration due to gravity on the surface of the Earth, the potential energy of the body is given, by, 𝑉 = 𝑚𝑔ℎ, In the cases of other forces like electric forces or magnetic forces, potential energy is, defined in terms of work done on the object. Work done on a body is usually stored as potential, energy. If a body is raised against gravitational force, a certain amount of work is required and it, will be stored in the body as potential energy. When the body is released, the potential energy is, converted into kinetic energy. In a way, the total amount of work done by a body is numerically, equal to its energy. If 100 J of work is done in raising a body above the ground level, the energy, of the body is 100 J., State Institute of Technical Teachers’ Training & Research, , |, , Page, , 64

Page 77 :
Applied Physics - !, , 3.2.2 Different Forms of Energy, Two basic types of energy namely kinetic energy and potential energy are sufficient to, describe all forms of energy. But it is convenient to refer to a particular combination of kinetic, energy and potential energy as its form. The major forms of energy include mechanical energy,, heat energy, light energy, sound energy electrical energy, magnetic energy, chemical energy, and, nuclear energy., a) Mechanical Energy, Mechanical energy is the energy of a system due to its motion, position, or configuration. It, is the sum of kinetic energy and potential energy of a system. A system can do work by utilizing, its mechanical energy. For example, machines use mechanical energy to do work., b) Heat Energy, An object possesses heat energy (thermal energy) due to the motion of molecules in it., The energy released when we burn wood, coal, oil, or gas is called heat energy. Steam possesses, heat energy which is capable of doing work. If you cook food in a pressure cooker by placing it, over a gas stove, the heat energy changes water into steam. The steam lifts the weight on the top, of the lid and whistles. This lifting of weight suggests that heat is a form of energy that is capable, of doing work. In 1765, James Watt, a young scientist, noted this phenomenon which led to the, invention of the steam engine in which heat energy was used to do work., In thermal power stations, it is the heat energy of burning coal that is used to generate, steam. The steam, in turn, runs the turbines of the generator and produces electric energy. All, automobiles use heat energy by burning petrol, diesel, or CNG for doing work. The food which, we consume burns slowly in our cells to produce heat energy., c) Light energy, Light energy is a form of electromagnetic radiation. When an excited electron in an atom, or a molecule undergoes a transition from a higher energy level to a lower energy level, the, difference in energy between the levels is sometimes emitted in the form of light. Light travels as, waves and it is capable of travelling through vacuum. The plants absorb light energy and convert, it into chemical energy (food) through a process called photosynthesis., State Institute of Technical Teachers’ Training & Research, , |, , Page, , 65

Page 78 :
Applied Physics - !, , d) Sound energy, Sound energy is produced when an object vibrates. A sound wave needs a medium to, travel through such as air, water, wood, or metal. When sound waves fall on the ear membrane,, they make it vibrate and we can hear the sound. When a supersonic plane breaks the sound, barrier (speed of sound in air), the sound waves produced by it, shake the buildings. Similarly,, the thunder of the cloud also shakes buildings. This shows that sound energy can also do work., e) Electrical energy, The energy produced by the movement of electrons is called electric energy. When, electric energy passed through an electric motor, it sets its axle in a circular motion. This circular, motion is utilized in running ceiling fans, juicers, grinders, etc. It is used for running electric, moped, vehicles. It is used in factories for running heavy machines. It is also used in heating, devices such as heaters, geysers, electric stoves, etc. It is also used in lighting bulbs., f) Magnetic energy, Magnetism is described by magnetic fields which are produced either by magnetic, materials (permanent magnets) or by electric currents. Energy stored in a magnetic field is called, magnetic energy. A magnet is capable of causing motion in magnetic substances. Iron cobalt,, nickel are examples of magnetic substances. Magnetic energy is used in electromagnets, electric, motors, electric generators, microphones, television tubes, telephones, etc. The cranes which lift, heavy loads of iron or separate iron scrap from waste materials use electromagnets., , g) Chemical Energy, Chemical energy is defined as the energy stored in the bonds between atoms or molecules, in a compound. When this compound undergoes a chemical reaction, the chemical energy stored, in the bonds will be released in the form of heat. The energy possessed by the fuels like coal, oil,, gas, etc. is chemical energy. The chemical energy of diesel, petrol, or CNG is capable of moving, vehicles. The food that we consume, possesses chemical energy which is utilized by our body to, do work., State Institute of Technical Teachers’ Training & Research, , |, , Page, , 66

Page 79 :
Applied Physics - !, , h) Nuclear energy, The binding energy of nucleons (neutrons and protons) in the nucleus is called nuclear, energy. The nucleus in an atom has an enormous amount of energy which holds the proton and, neutrons together. When a heavy nucleus splits into light nuclei or two light nuclei combine to, form one nucleus, it releases energy. Nuclear fission or fusion releases nuclear energy in the, form of heat and light energy. In nuclear power stations, nuclear energy is used to generate, electric energy. In the case of an atom bomb or hydrogen bomb, nuclear energy is used for, destructive purposes., , 3.2.3 Solar Energy, Solar energy is radiant light and heat from the Sun. Solar energy is created by nuclear, fusion that takes place in the sun. The primary source of all kinds of energy on Earth is solar, energy. Solar energy provides wind energy, tidal energy, and energy of sea waves. Solar energy, causes the evaporation of water, which in turn leads to the water cycle. The phenomenon of, photosynthesis is not possible without solar energy. It is necessary for life on Earth and can be, harvested for human use in many ways. Solar cells absorb sunlight and convert solar energy into, electrical energy. Solar cooker, Solar water heater, etc. utilizes heat energy present in the solar, radiation., , 3.2.4 Transformation of Energy, Energy transformation is the process of converting one form of energy into another form., There are various types of energy all around us and these energy sources can be converted from, one form to another as explained below:, , , Conversion of Potential energy into kinetic energy and vice versa, , , , Conversion of Light energy into heat energy., , , , Conversion of Electrical energy into mechanical energy, light energy, heat energy, etc., , , , Conversion of chemical energy into electrical energy., , , , Conversion of mechanical energy into electrical energy, sound energy, etc., , State Institute of Technical Teachers’ Training & Research, , |, , Page, , 67

Page 80 :
Applied Physics - !, , , , Conversion of Nuclear energy into light energy and heat energy., , , , Conversion of Solar energy into heat energy, chemical energy, and electrical energy., , Some examples of energy transformation are given below:, a), , When hands are rubbed, the mechanical energy is converted into heat energy., , b), , When we wind a watch, the mechanical energy of the hand changes into the potential, energy of spring and which in turn changes to kinetic energy and drives the hands of, the clock., , c), , The potential energy of water in hydel dams is ultimately converted into electrical, energy., , d), , When a torch is switched on, the chemical energy of the cells changes into electrical, energy., , e), , In thermal power stations, the chemical energy changes into electric energy., , f), , In lighting devices, such as filament bulbs, CFL, the electric energy is converted into, light energy., , g), , When varying electric impulses are passed through the speaker of the audio system, it, changes into sound energy., , h), , During the charging of lead-acid batteries, the electric energy is converted into, chemical energy., , i), , During the oscillations of a simple pendulum, potential energy is converted into, kinetic energy and vice versa., , j), , When a laser beam is used to cut metal, light energy is converted into heat energy, , State Institute of Technical Teachers’ Training & Research, , |, , Page, , 68

Page 81 :
Applied Physics - !, , Conceptual Learning 3.4, i., , Find more examples of conversion of mechanical energy into heat energy., , ii., , Find more examples of conversion of mechanical energy into sound energy., , iii. Explain all the forms of energy conversion when we stretch an ‘arrow’., iv. Write the possible energy transformations in the hydroelectric project., v., , Is there any heat generation, when chemical energy is converted into electric, energy? Give example., , vi., , Find an example for the conversion of electric energy into magnetic energy., , vii., , Write the energy conversion in photovoltaic cells., , viii. Is it possible to convert sound energy into electric energy?, ix., , Give an example of the conversion of chemical energy into mechanical energy., , x., , What energy transformation happens in photosynthesis, , xi., , Can you explain what kind of energy is available in fossil fuels and biogas?, , 3.2.5 Law Conservation of Energy, The Law of conservation of energy, states that energy can neither be created, nor be destroyed, but can be converted from, one form to another. In other words, the, total energy of an isolated system remains, constant. A simple example involves a, stationary car at the top of a hill. As the car, moves down the hill, it moves faster and so, its kinetic energy increases and its potential, energy decreases. On the way back up the, hill, the car converts kinetic energy to, potential energy. In the absence of friction,, the car should end up at the same height as, , Fig. 3.1 Total energy of a body freely falling, from a height above the ground level, , State Institute of Technical Teachers’ Training & Research, , |, , Page, , 69

Page 82 :
Applied Physics - !, , it started. Hence the total energy which is the sum of kinetic energy and potential energy remains, constant. Now, we are going to prove the law of conservation of energy in the case of a freely, falling body., Consider a body of mass m, initially placed at height h above the ground level as shown, in Fig. 3.1.Let the body is allowed to fall freely from its initial position A. In the case of a freely, falling body, the total energy is the sum of its kinetic energy and potential energy. As the body, moves under gravity, its velocity and hence, kinetic energy increases. But at the same time, the, height of the body from the ground decreases, and hence, the potential energy decreases., At Point A, Velocity at point A, 𝑣 = 0, Kinetic energy at point A, 𝐾 = 𝑚𝑣, , =0, , The potential energy at point A, 𝑉 = 𝑚𝑔ℎ, Total energy at point A, 𝐸 = 𝐾 + 𝑉, , ------------ (1), , 𝐸 = 0 + 𝑚𝑔ℎ = 𝑚𝑔ℎ, At Point B, , Let B be a point at a distance x from point A. The velocity at point B, 𝑣 can be, calculated using the equation, 𝑣 = 𝑢 + 2𝑎𝑠., 𝑣= 𝑣 ;, 𝑣, , 𝑢 = 𝑣 = 0;, , 𝑎 = 𝑔; 𝑠 = 𝑥;, , = 2𝑔𝑥, , Kinetic energy at point B, 𝐾 = 𝑚𝑣, , =, , 𝑚 × 2𝑔𝑥 = 𝑚𝑔𝑥, , The potential energy at point A, 𝑉 = 𝑚𝑔(ℎ − 𝑥), Total energy at point A, 𝐸 = 𝐾 + 𝑉, , ---------- (2), , 𝐸 = 𝑚𝑔𝑥 + 𝑚𝑔(ℎ − 𝑥) = 𝑚𝑔ℎ, At point C, , Let C be a point on the ground. The velocity at point C, 𝑣 can be calculated using the, equation, 𝑣 = 𝑢 + 2𝑎𝑠., , State Institute of Technical Teachers’ Training & Research, , |, , Page, , 70

Page 83 :
Applied Physics - !, , 𝑣= 𝑣 ;, , 𝑢 = 𝑣 = 0;, 𝑣, , 𝑎 = 𝑔; 𝑠 = ℎ;, , = 2𝑔ℎ, , Kinetic energy at point C, 𝐾 = 𝑚𝑣, , =, , 𝑚 × 2𝑔ℎ = 𝑚𝑔ℎ, , The potential energy at point A, 𝑉 = 0, Total energy at point A, 𝐸 = 𝐾 + 𝑉, 𝐸 = 𝑚𝑔ℎ + 0 = 𝑚𝑔ℎ ---------- (3), It is clear from equations (1), (2), and (3) that 𝐸 = 𝐸 = 𝐸 . Hence total energy of the, freely falling body remains constant at every point on its path., , 3.3 POWER, The word "power" is often used to describe someone in authority like a king or a dictator., It's also used to describe someone or something very strong. We sometimes refer to electricity as, power in our daily life. We might also talk about the power of water pumps, vehicles, electrical, appliances, etc. In physics, power has a definite meaning and we can understand it through a, learning activity., , Conceptual Learning 3.5, Imagine two pumps (motor) with power 1HP and 2 HP and two tanks with the same volume, situated at the same height. Each motor pumps the tanks simultaneously. What do you, observe? Give reason. What is your inference? Can you define power?, , Power is defined as the rate at which work is done.In other words, power is the work, done in unit time. If W is the work done in a time t, the average power is given by, 𝑤𝑜𝑟𝑘, 𝑡𝑖𝑚𝑒, 𝑊, 𝑃=, 𝑡, , 𝑃𝑜𝑤𝑒𝑟 =, , State Institute of Technical Teachers’ Training & Research, , |, , Page, , 71

Page 84 :
Applied Physics - !, , But work done is defined as the product of force and displacement., 𝑊 = 𝐹𝑆, ∴, , 𝑃=, , 𝐹𝑆, 𝑡, , But the velocity of the body is given by, 𝑣=, , 𝑆, 𝑡, , ∴ 𝑃 = 𝐹𝑣, 𝑃𝑜𝑤𝑒𝑟 = 𝐹𝑜𝑟𝑐𝑒 × 𝑣𝑒𝑙𝑜𝑐𝑖𝑡𝑦, Power can also be defined as the energy converted or transferred in unit time., 𝑒𝑛𝑒𝑟𝑔𝑦, 𝑃𝑜𝑤𝑒𝑟 =, 𝑡𝑖𝑚𝑒, Power is a scalar quantity. The SI unit of power is joule/second or watt (W)., 1 watt = 1 joule/second., Other commonly used units are, 1 kilowatt (kW) = 103 watt, 1 megawatt (MW) = 106 watt, 1 Horsepower (hp) = 746 watt, The energy consumption of electrical devices is expressed in kilowatt-hour (kWh). Kilo, watt-hour is not the unit of power, but it is a practical unit of electrical energy., Example 3.1, Calculate the work done in lifting a mass 5 Kg vertically through 8m., Solution:, Given m = 5 Kg, h = 8 m, 𝑊 = force × vertical displacement = 𝑚𝑔ℎ = 5 × 9.8 × 8 = 392 J, Example 3.2, A body of mass 5 kg initially at rest is subjected to a force of 20 N. What is the kinetic energy, acquired by the body at the end of 10 s?, State Institute of Technical Teachers’ Training & Research, , |, , Page, , 72

Page 85 :
Applied Physics - !, , Solution:, Given, m = 5 kg, F = 20 N, t = 10s, u = 0, 𝐹 = 𝑚𝑎, 𝑎=, , 𝐹, 20, =, = 4 𝑚⁄𝑠, 𝑚, 5, , 𝑣 = 𝑢 + 𝑎𝑡 = 0 + 4 × 10 = 40 𝑚⁄𝑠, 𝐾=, , 1, 1, 𝑚𝑣 = × 5 × 40 = 4000 J, 2, 2, , Example 3.3, A work 900 J is done when a force of 30 N is applied to a body. Calculate the distance through, which the body moves., Solution:, Work done (W) = 900 J, Force (F) = 30 N, 𝑊 = 𝐹. 𝑆, Distance covered, 𝑆 =, , =, , = 30 𝑚, , Example 3.4, The momentum of a body of mass 10 kg is 30 SI units. Calculate its kinetic energy., Solution:, Momentum, p =mv = 30 kgm/s., Mass m = 10 kg, Velocity = p/m = 3m/s, Kinetic energy K = ½ mv 2 = ½ x 10 x 32 = 45 J, The relation E = p2/ 2m can also be used to get the result., Example 3.5, An engine develops 10 kW of power. How much time will it take to lift a mass of 200 kg to a, height of 40 m?, , State Institute of Technical Teachers’ Training & Research, , |, , Page, , 73

Page 86 :
Applied Physics - !, , Solution:, Force acting on a body of mass 200 kg, F = mg = 200 x 9.8 = 1960 N, Work done W = F.S = 1960 x 40 = 78400 J, Power = 10 kW = 10000 W., Power = work/time, Time taken = work/power = 78400/10000 = 7.84 s, Example 3.6, An electric motor raises 200 kg of water to a tank at a height 30 m above ground level in a time, of 3 minutes. If the efficiency of the pump is 87 %,what is the power of the motor (designed by, the company/ manufacturer)?, Solution:, Output energy of the pump = mgh = 200 x 9.8x 30 = 58,800 J, Time = 3 min = 3 x 60 = 180 s, Output power of the pump = energy /time = 58800/180 = 326.67 W, Efficiency = output power /input power = 87% = 87/100 =0.87, Input power = output power /0.87 = 326.67/0.87 = 375.48 W, Power of the motor = 375.48 W, , Conceptual Learning 3.6, Learn the problem given in example 3.6 and evaluate the following, i., , 375.48W motor pumps only 200 kg of water in 3 minutes and shows output power, of 326.67W. If the motor has an efficiency of 100% what would be the input power?, , ii. Power of a motor pump is commonly expressed in horse power (hp). Convert the, power of the motor obtained in watts into horse power., iii. Why the motor has an efficiency of 87% instead of 100 %., iv. List the factors which reduce the efficiency of a motor., v. If the motor has 100 % efficiency, calculate the pumping rate., vi. If the efficiency of a motor is 60%, 70%, etc. comment your observations., vii. How much time will be taken by a half hp motor to pump water into a 100-litretank, placed at a height of 10 m? The efficiency of the motor is 50%., State Institute of Technical Teachers’ Training & Research, , |, , Page, , 74

Page 87 :
Applied Physics - !, , Example 3.7, A cricket ball of mass 0.3 kg is thrown vertically up with a velocity of 14.7 𝑚⁄𝑠. Calculate the, K.E and P.E of the ball after one second., Solution:, Mass of the ball m = 0.3 kg, Initial velocity u = 14.7 m/s, a = g= 9.8 m/s2;t = 1 s, The velocity after 1 s, v = u +at = 14.7-9.8 x 1= 4.9 m/s, K.E after 1 s is K = mv 2 = x 0.3 x(4.9) 2 = 3.6 J, Vertical displacement of the ball after 1 second is, h = ut- gt 2 = 14.7 x 1- 9.8 x 1 = 9.8 m, P.E after 1 s = mgh = 0.3 x 9.8 x 9.8 = 28.81 J, , Example 3.8, An elephant lifts a body of mass 1000 kg through a vertical height of 3 m in 10 s. What is, power?, Solution:, Work done = mgh= 1000 x 9.8 x 3 =29400 J, Power = work /time = 2940 W, , 3.4 FRICTION, It is a common experience that, a rolling ball comes to rest after moving a finite distance., It is clear that in order to stop a body, an external force is required. Did you think about the, external force? The opposing force for the movement of the ball is supplied by the surface and is, called frictional force. Ordinarily, when one body slides over another, there is some opposition, to the relative motion. This is referred to as friction. Friction is a force between solid surfaces in, contact. Friction is tangential to the surface and points opposite to the direction of motion (or, intended motion).The property by which an opposing force is generated between two surfaces in, contact with bodies in relative motion is called friction., State Institute of Technical Teachers’ Training & Research, , |, , Page, , 75

Page 88 :
Applied Physics - !, , 3.4.1 Causes of friction, Friction is a force resisting motion of an object when in contact with another. This, resistive force is caused by the surface roughness of the contact area of the materials, molecular, attraction or adhesion between materials, and deformations in the materials. Most friction results, because the surfaces of materials being rubbed together are not completely smooth. If you looked, at what seems to be a smooth surface under a powerful microscope, you would see bumps, hills,, and valleys that could interfere with a sliding motion., The friction appears because of the interaction between the charged particles of the two, bodies near the surfaces of contact. Molecular attraction or adhesion between the material, surfaces leading to a resistive force between surfaces in relative motion. When two bodies come, into contact, due to the irregularities of the surfaces, the area of contact is less than the actual, area of the surfaces. This causes very high pressure at the point of contact. The high pressure, causes deformation of the surface of the material and eventually increases the resistance to, motion., , 3.4.2 Types of friction, Friction is generally classified into two main categories namely static friction and kinetic, friction., a) Static friction, The frictional force comes into, play when one body tends to move over, the surface of another, but the actual, motion that has yet not started is called, static friction. For example, suppose you, are trying to push a heavy almirah on the, floor to take it out of a room. It does not, slide until the force applied is greater than, a minimum value. As long as almirah is, , Fig. 3.2Friction opposes the relative motion, between the sliding body and the surface, , State Institute of Technical Teachers’ Training & Research, , |, , Page, , 76

Page 89 :
Applied Physics - !, , at rest, the force of static friction (fs) is equal and opposite to the applied force (f). As the applied, force increases, the force of static friction also increases. This means that the magnitude of static, friction adjusts its value according to the applied force. Thus, static friction is a self-adjustable, force., However, the frictional force cannot go beyond a maximum value. When the applied, force exceeds this value, the body starts moving over the surface. The maximum value of static, friction before the body starts moving over a surface is called limiting friction. The limiting, friction, 𝑓, , is directly proportional to the normal force between the two bodies., , 𝑓, , ∝ 𝑁, , 𝑓, , =𝜇 𝑁, , The constant of proportionality 𝜇 is called the coefficient of static friction and its value depends, on the material and nature of the two surfaces in contact. The static friction 𝑓 is always less than, or equal to the limiting friction 𝑓, , ., 𝑓 ≤𝑓, , =𝜇 𝑁, , b) Kinetic or dynamic friction, Kinetic or dynamic friction is the opposing force that comes into play when one body is, moving over the surface of another body. The magnitude of kinetic friction, 𝑓 is directly, proportional to the normal force acting between the two bodies., , 𝑓, 𝑓, , ∝ 𝑁, =𝜇 𝑁, , The constant of proportionality 𝜇 is called the coefficient of kinetic friction and its, value also depends on the material and nature of the two surfaces in contact. If the surfaces are, smooth 𝜇 will be small and if surfaces are rough 𝜇 will be large., Kinetic friction is classified into two types – sliding friction and rolling friction., a) Sliding friction: The frictional force that comes into play when one body is actually, , sliding over the surface of the other body is called sliding friction., State Institute of Technical Teachers’ Training & Research, , |, , Page, , 77

Page 90 :
Applied Physics - !, , b) Rolling friction: The frictional force that plays when one body is actually rolling, over the surface of the other body is called rolling friction. Rolling friction is less, than sliding friction., , 3.4.3 Laws of friction, Experimental observations regarding the nature of the force of friction between the, surfaces can be summarized into a small number of laws called laws of friction., 1. The Force of friction depends on the nature of surfaces in contact., 2. Friction is independent of the area of contact as long as the normal force is the same., 3. The maximum force of static friction is directly proportional to the normal force acting, between the two bodies in contact., 4. Kinetic friction is directly proportional to the normal force acting between the two bodies, in relative motion., 5. The direction of kinetic friction on a body is opposite to the velocity of the body., 6. The magnitude of kinetic friction is independent of the velocity of motion of the body., 7. The coefficient of kinetic friction is always less than the coefficient of static friction for, the same pair of surfaces., , 3.4.4 Advantages of friction, i., , It is the friction between the ground and the feet that help us to walk, , ii., , It helps us to hold things., , iii. The friction between tyres and the road helps us to stop the vehicle when the brake is, applied., iv. Nails and screws join two surfaces due to the force of friction., v., , Without friction, it is impossible to climb a tree or fix a nail on the wall., , 3.4.5 Disadvantages of friction, i., , Friction slows down the motion of moving objects., , ii., , Friction produces unnecessary heat leading to the wastage of energy., , iii. It decreases the efficiency of the machines., iv. It causes wear and tear for the moving parts of the machines., v., , Friction sometimes creates fire accidents like forest fires, , State Institute of Technical Teachers’ Training & Research, , |, , Page, , 78

Page 91 :
Applied Physics - !, , 3.4.6 Methods to reduce friction, Friction is a necessary evil. Friction is useful while we walk, write, play, run, etc., but it, can also be harmful to us like fire accidents, wear, and tear. It is sometimes necessary to reduce, friction to avoid the wear and tear of machines. Let us discuss some methods to reduce friction., a) Lubrication, , When the gap between two surfaces is filled with oil or grease, irregularities become, filled with this and the friction reduces. This process is called lubrication and the substance used, for this are called lubricants. The lubricants are selected based on the nature of the machines. A, modern lubricant is a mixture of mineral oil, vegetable oil, and colloidal thin oil. For light, machinery, oils are used while for heavy machines grease is used. For light machinery like, watches, sewing machines, etc., thin oil is used. In very heavy machinery, solid lubricants like, graphite are used., b) Polishing of rough surfaces, A hard substance is used to grind and remove the irregularity on the soft surface., Examples including polishing of wooden surfaces, tiles, marbles, etc. Sandpaper is also used for, polishing to a fine level. Harsh chemical treatments are sometimes done to reduce irregularities, on surfaces. When the surface becomes smooth, the contact pressure decreases, and hence, friction reduces., c) Use of ball bearings in moving parts, It is our common experience that it is easier to role a body than to slide it along the, ground. This is the principle in which ball bearings work. Hard steel balls place between the, moving parts like coaxial cylinders. The balls rotate as the cylinders turn relative to each other., This considerably reduces friction., , State Institute of Technical Teachers’ Training & Research, , |, , Page, , 79

Page 92 :
Applied Physics - !, , 3.5 HEAT, Conceptual Learning 3.7, i. Dip your hand in some cold water and hot water. What do you feel?, ii. We use the words like very cold, warm, very warm, burning hot, etc. in daily life. Did you, think about how do you feel, the body is cold, hot warm, etc., iii. What is the direction of heat flow, if we touch a hot body? Justify your answer., iv. Is possible to transfer heat from a cold body to a hot body?, , When we rub our hands for some time, they become warm. When a block slides over a, rough surface, it becomes warm. Where does the mechanical energy go? It goes into the internal, energy of the body. The internal energy of a body is the sum of kinetic energy and potential, energy of constituent atoms or molecules. A cold body absorbs energy to become hot. A hot, body has more internal energy than the otherwise identical cold body., When a hot body is kept in contact with a cold body, the cold body warms up and the hot, body cools down. Energy is transferred from the hot body to the cold body when they are placed, in contact. This transfer of energy is a non-mechanical process. The energy transferred from one, body to another without any mechanical work involved is called heat. If no transfer of heat takes, place between two bodies in contact, then they are said to be in thermal equilibrium., , 3.5.1 What is Temperature?, The temperature of a substance is the degree of hotness or coldness on some chosen, scale. Heat energy and temperature are different. When heat energy is given to a substance its, temperature may increase and when heat energy is taken from the substance its temperature may, fall. All bodies in thermal equilibrium are assigned the same temperature. A hotter body is, assigned a higher temperature than a colder body. Thus, the temperature of two bodies decides, the direction of heat flow when two bodies are put in contact. Heat flows from the body at a, higher temperature to a body at a lower temperature., , State Institute of Technical Teachers’ Training & Research, , |, , Page, , 80

Page 93 :
Applied Physics - !, , Heat is an invisible energy that causes the sensation of hotness or coldness. An object, will appear cold only if the heat from our body flows into it. In the CGS system, the unit of heat, is calorie. The SI unit of heat is Joule. One calorie is equal to 4.2 J. The effects of heat energy, are:, a), , Heat energy brings about change in temperature, , b), , Heat energy brings about change in dimension., , c), , Heat energy brings about change in the state., , Conceptual Learning 3.8, 1. Prepare a chart showing examples for the effects of heat energy, 2. Do you think that heat energy brings about chemical change? Write a brief note on it., 3. The sun is a source of heat energy. Find out the other sources of heat energy., , 3.5.2 Temperature scales, A temperature scale is a way to indicate or measure temperature relative to a starting, point and a unit of measurement. The temperature scale chosen must be precise, consistent, and, accurate. All temperature scales make use of some physical property that changes with, temperature. The major temperature scales used are the Celsius, Fahrenheit, and Kelvin scales., Most temperature scales have two fixed points: lower fixed point and upper fixed point., a) Celsius Scale, Celsius or centigrade scale is a temperature scale based on the freezing point of water and, the boiling point of water. The temperature corresponding to the freezing point of water is taken, as the lower fixed point and it is taken as 0 0C. The boiling point of water is taken as upper fixed, pint and is given a value of 100 0C. The interval between these two temperatures is divided into, 100 equal parts and one division is called one degree Celsius (1 0C)., b) Fahrenheit scale, In the Fahrenheit scale, the freezing point of water is taken as 32 0F, and the boiling point, of water is 212 0F. The interval is divided into 180 equal parts. Each division is called one degree, Fahrenheit (10F)., State Institute of Technical Teachers’ Training & Research, , |, , Page, , 81

Page 94 :
Applied Physics - !, , c) Kelvin scale, Kelvin scale is a temperature scale based on absolute zero of temperature. Absolute zero,, or 0K, is the lowest possible temperature for any substance and it corresponds to a temperature, of −273.15° on the Celsius scale. In the Kelvin scale, the freezing point of water is taken as 273K, and the boiling point of water is 373 K. Magnitude of a degree in the Kelvin scale and Celsius, scale are equal. Kelvin is the SI unit of temperature., , Fig. 3.3 Comparison of Celsius scale, Fahrenheit scale and Kelvin scale, , 3.5.3 Conversion between temperature scales, The relation connecting Celsius, Fahrenheit, and Kelvin scales is given by the following, formula where C stands for temperature in Celsius, F stands for temperature in Fahrenheit and K, stands for temperature in Kelvin scale., , State Institute of Technical Teachers’ Training & Research, , |, , Page, , 82

Page 95 :
Applied Physics - !, , 𝐶−0, 𝐹 − 32, 𝐾 − 273, =, =, 100, 180, 100, 𝐶, 𝐹 − 32, 𝐾 − 273, =, =, 5, 9, 5, The equation to convert between Celsius and Kelvin temperature scales is given by, 𝐾 = 𝐶 + 273, The equation to convert between Celsius and Fahrenheit temperature scales is given by, 𝐹 = 1.8 𝐶 + 32, , 3.5.4 Thermometers, A thermometer is a device used to measure temperature. The science of measuring, temperature is known as thermometry. Any physical property that depends on temperature, and, whose response to temperature is reproducible, can be used as the basis of a thermometer. The, properties usually chosen for the purpose are:, i. Change in length, volume, or pressure., ii. Electrical changes such as a change in resistance and thermoelectric effect, iii. Change of state, colour, etc., , 3.5.5 Classification of thermometers, According to its measurement principles, thermometers are classified into different, categories as listed below:, 1. The liquid in the glass thermometer (Mercury thermometer, alcohol thermometer, etc.), 2. Constant volume gas thermometer, 3. Constant pressure gas thermometer, 4. Resistance thermometer, 5. Thermoelectric thermometer or Thermocouple, 6. Pyrometers, 7. Silicon diode thermometer, 8. Bimetallic thermometer, State Institute of Technical Teachers’ Training & Research, , |, , Page, , 83

Page 96 :
Applied Physics - !, , 3.5.6 Mercury Thermometer, It is the common thermometer used in laboratories and the medical field., field It works on the, principle of thermal expansion of liquids. The thermometer consists of a very fine glass tube, having a very small bore (capillary tube) as shown in Fig. 3.5.. The capillary tube consists of a, thin glass bulb at one end. The bulb is filled with mercury. The other end of the capillary tube is, sealed. The capillary tube is protected by a thick glass tube called the stem. Markings, arkings are made, onn the stem. These markings are called graduations or degrees., , As the glass bulb and the liquid are heated, the volume of both the glass tube and mercury, increase with temperature.. The mercury expands more than glass. Hence, the liquid level rises, with the increase in temperature and falls when the temperature is lowered. The practical range, of mercury thermometersis -30 0C to 250 0C., , 3.5.7 Pyrometers, The name pyrometer is given to those thermometers which are used for measuring, temperatures above 500 0C. The familiar pyrometers are total radiation pyrometers and optical, pyrometers. A pyrometer, also known as an infrared thermometer or radiation, adiation thermometer,, thermometer or, non-contact thermometer is used to detect the temperature of an object’s surface temperature,, which depends on the radiation (infrared or visible) emitted from the object. Pyrometers act as, photo detectors because of the property of absorbing energy and measuring EM wave intensity at, any wavelength. A pyrometer is usef, useful for measuring moving, extremely hot, or hard-to-reach, objects., , State Institute of Technical Teachers, Teachers’ Training & Research, , |, , Page, , 84

Page 97 :
Applied Physics - !, , The basic principle of the pyrometer is that it measures the object’s temperature by, sensing the heat radiation emitted from the object without making contact with the object. It, records the temperature level depending upon the intensity of radiation emitted. The pyrometer, has two basic components like optical systems and detectors that are used to measure the surface, temperature of the object., , Fig. 3.6 Schematic diagram of a pyrometer, Infrared pyrometers are made up of pyroelectric materials like polyvinylidene fluoride (PVDF),, triglycine sulfate (TGS), and lithium tantalate (LiTaO3). This radiation can be directed to a, thermocouple to convert into electrical signals. The advantages of pyrometer are, a) It can measure the temperature of the object without any contact with the object. This is, called non-contact measurement., b) It has a fast response time., c) Good stability while measuring the temperature of the object., d) It can measure the temperature of different types of objects at variable distances., Pyrometers are used in different applications such as,, a), , To measure the temperature of moving objects or constant objects from a greater, distance., , b) In metallurgy industries, c), , In smelting industries, , State Institute of Technical Teachers’ Training & Research, , |, , Page, , 85

Page 98 :
Applied Physics - !, , d) Hot air balloons to measure the heat at the top of the balloon, e) Steam boilers to measure steam temperature, f) To measure the temperature of liquid metals and highly heated materials., g), , To measure furnace temperature., , Example 3.9, Perform the appropriate temperature conversions to fill in the blanks in the table below., Celsius (°), a., , Fahrenheit (°F), , Kelvin (K), , 0, , b., , 212, , c., , 0, , d., , 78, , e., , 12, , Solution:, Use the relation =, , =, , for temperature conversion., , Celsius (°C), , Fahrenheit (°F), , Kelvin (K), , a., , 0, , 32, , 273, , b., , 100, , 212, , 373, , c., , -273, , -459, , 0, , d., , 26, , 78, , 299, , e., , -11, , 12, , 267, , Example 3.10, The normal human body temperature is 98.6 0F. Convert the temperature in 0C and Kelvin, Solution:, Given, F = 98.6 0F, In Celsius scale, C =, , (98.6 − 32) = x 66.6= 37 0C, , In Kelvin scale, T = 273+ 37 = 310 K, State Institute of Technical Teachers’ Training & Research, , |, , Page, , 86

Page 99 :
Applied Physics - !, , 3.5.8 Modes of heat transfer, Heat may be transferred from one point to another in three different ways namely, conduction, convection, and radiation., , (a) Conduction, If one end of a metal rod is heated, the temperature of the other end gradually increases., Heat is transferred from one end of the rod to the other end. This transfer takes place due to, molecular collisions and there is no movement of particles. Transfer of heat from one place to, another or one end (hot end) to the other end (cold end) of the substance, without the actual, movement of particles, is called conduction. Conduction is the slowest mode of heat transfer., Conduction is most significant in solids and less in liquids and gases, due to the space between, molecules. Substances that conduct heat are called good conductors and which do not conduct, are called poor conductors or insulators. Metals are good conductors whereas gases and nonmetals are poor conductors. Aluminium, gold, copper, silver are examples of conductors. Silver, is the best conductor of heat. Asbestos, rubber, glass paper, etc. are examples of insulators. The, ability of a material to conduct heat is measured by a quantity called thermal conductivity of the, material., , Consider a metallic rod of the area of cross-section A. Suppose one end of the rod is heated and, an amount of heat Q is conducted from the hot end to the cold end of the rod. Consider a small, element of the rod of length dx and a temperature difference of dT exists between its ends. The, quantity of heatflowing through the rod depends on its area of cross-section, temperature, gradient (, , ) and time (t) for which heat flows. It can be mathematically expressed as, 𝑄∝ A, , 𝑑𝑇, t, 𝑑𝑥, , State Institute of Technical Teachers’ Training & Research, , |, , Page, , 87

Page 100 :
Applied Physics - !, , 𝑄=𝜆A, , 𝑑𝑇, t, 𝑑𝑥, , Here the constant of proportionality λ is called the thermal conductivity of the material., 𝜆 =, , 𝑄, 𝑑𝑇, 𝐴, 𝑡, 𝑑𝑥, , The SI unit of λ is Js-1m-1K-1or Wm-1K-1. Metals have a high value of thermal conductivity, due to the presence of a large number of free electrons. The thermal conductivities of some, metals are given in the table below., Table 3.1: Thermal conductivities of some metals, , Material, , Thermal Conductivity, K (Wm-1K-1), , Iron, , 67, , Aluminium, , 200, , Copper, , 385, , Gold, , 397, , Silver, , 414, , Practical applications of thermal conductivity are:, i., , Cooking utensils are made of metals and their handles are made of wood. This is, because metals are good conductors of heat, while wood is a bad conductor of heat., , ii., , When we take a metal ice tray and a package of frozen food from the freezer of the, refrigerator, the metal tray feels colder than the package. This is because metal is a, good conductor of heat and it removes heat from our hands much faster., , iii. Houses made of hollow brick walls are cooler than concrete walls., iv. During winter birds swell their feathers. In doing so the air trapped between the, feathers prevent the loss of heat from their body. This is because air is a poor, conductor of heat., v., , Ice is packed in sawdust or gunny bags. This is because air trapped in them prevents, loss of heat and so ice does not melt. Air is a poor conductor of heat., , State Institute of Technical Teachers’ Training & Research, , |, , Page, , 88

Page 101 :
Applied Physics - !, , Conceptual Learning 3.9, Give an appropriate explanation to the following cases based on conduction., 1. In cold countries, double glass window panes are used., 2. Two thin woolen blankets are warmer than a thick woolen blanket., (b) Convection, Convection is the phenomenon in which heat is transferred from one place to another by, the actual movement of the particles of a heated substance. The convection process is faster than, conduction. Transfer of heat by convection mode takes place in liquids and gases. If we boil a, kettle of water, the hot water molecules become less dense and move to the top surface. At the, same time dense water molecules at the top move to the bottom. Thus, a convection current gets, established and the entire water gets heated. The rate at which heat is transferred from the, surface of the fluid is given by the relation, 𝑄, = ℎ𝐴∆𝑇, 𝑡, where A is the surface area of fluid, ∆𝑇 is the temperature difference between the fluid at the, upper and lower surfaces and h is a constant called convection coefficient. The value of h, depends on the shape of the surface and whether the surface is horizontal or vertical., The same process is taking place in air movement also. As dense cool air enters a room, through doors and windows, the less dense hot air gets exhausted through the ventilators in the, room. The reason for convectional current is due to the unequal heating of the fluid. This is the, basic principle for the formation of winds. Summer and winter monsoons on the earth are due to, the transfer of heat by convection and radiation, rotation of the earth, and the earth’s gravity., Convection is classified as natural convection and forced convection. Natural convection, is a process in which fluid motion is generated due to differences in densities and temperature, gradient. Forced convection is a convection process in which fluid motion is generated by an, external source (like a pump, fan, suction device, etc.). The main mechanism of heat transfer, inside a human body is forced convection. The heart serves as the pump and blood as the, circulating fluid. The heat from our body is lost to the atmosphere through all three processes –, State Institute of Technical Teachers’ Training & Research, , |, , Page, , 89

Page 102 :
Applied Physics - !, , conduction, convection, and radiation. But our blood circulation system transports just the, required amount of heat to maintain a constant body temperature., (c) Radiation, Radiation is the fastest mode of heat transfer which does not require a material medium., All bodies radiate energy in the form of electromagnetic waves. The energy transferred in this, mode is often called thermal radiation. The type of radiation associated with the transfer of heat, energy from one location to another location is often known as infrared radiation. This is because, the wavelength range of thermal radiation is from 800 nm to 400 µm, which belongs to the, infrared region. Some basic properties of thermal radiations are given below., a) They travel in straight lines with the speed of light (3x108m/s), b) A material medium is not necessary for propagation., c) They do not heat the medium through which they are travelling., d) They can be reflected and refracted just as light., e) They also exhibit the phenomena like interference, diffraction, and polarization., f) Thermal radiations have longer wavelengths than visible light., In the radiation process, a hot body emits thermal radiation in all directions. Emitted, radiation travels through space and falls on another body. The body absorbs thermal radiation, and gets heated up. The heat from the sun reaches the earth by radiation., , 3.5.9 Specific heat capacity of a substance, , Conceptual Learning 3.10, The same amount of milk and water are kept in two beakers and heated over two gas burners, by supplying an equal amount of heat. But it is observed that the rise in temperature of the, milk is more than that of water. Can you give the reason for this?, , State Institute of Technical Teachers’ Training & Research, , |, , Page, , 90

Page 103 :
Applied Physics - !, , When heat is supplied to a body, its temperature increases. Temperature is a direct, measure of the kinetic energy of molecules in the body. The kinetic energy of molecules, increases with the absorption of more and more heat energy and as a result, its temperature, increases. Gain or loss of heat energy by a body is measured in terms of temperature rise or fall., Now, the question is by how much will the temperature of an object increase or decrease by the, gain or loss of heat energy?, , The amount of thermal energy absorbed or given out by a body cannot be measured, directly by an instrument. Quantities of heat must be measured by the effect they produce. The, heat capacity of a body is the quantity of heat required to raise the temperature of the body by, one kelvin. If you see two materials, one of which absorbs heat faster than the other, then it is, because of the difference in their heat capacities. So, different materials when supplied by the, same amount of heat would increase in temperatures by different magnitudes. The amount of, heat (Q)absorbed by a body depends on the mass of the body (m), change in temperature (∆𝑇),, and nature of the material. Hence,, 𝑄 ∝ 𝑚∆𝑇, 𝑄 = 𝐶𝑚∆𝑇, where the constant C is called the specific heat capacity of the substance. The specific heat, capacity of a substance is defined as the quantity of heat required to raise the temperature of the, unit mass of a substance through one kelvin., 𝐶=, , 𝑄, 𝑚∆𝑇, , The SI unit of specific heat capacity is s Jkg-1K-1. Consider an example to understand, specific heat capacity better. The specific heat capacity of water is about 4200 Jkg -1K-1.This, means that it will take 4200 J of energy to raise the temperature of 1 kg of water by 1 degree, kelvin or degree Celsius. Suppose now you want to boil 2 kg of water in a kettle from room, temperature of 20∘C to100∘C. This will require Q = mCΔT=2×4200×80=672kJ of energy., Suppose the kettle has a power rating of 2KW. Then the time taken to boil 2 kg of water will be, 336 s or 5.6 mins., State Institute of Technical Teachers’ Training & Research, , |, , Page, , 91

Page 104 :
Applied Physics - !, , Table 3.2: Specific heat capacity of some substances, Substance, , Specific heat capacity, (Jkg-1K-1), , Water, , 4200, , Aluminium, , 924, , Iron, , 448, , Copper, , 378, , Silver, , 234, , Take one kg of water and one kg of milk in separate jars and the same amount of heat is, supplied to both jars. Measure the temperature rise in both the jar, obviously the temperature of, milk will rise quickly than water. For the same amount of heat and the same amount of material,, milk shows a higher temperature than water. This is due to the specific heat capacity of milk, (C=3.93 kJkg-1K-1) is lower than that of water(C=4.18 kJkg-1K-1)., , Conceptual Learning 3.11, 1. The same amount of milk and water at the same temperature is allowed to cool. Which will, cool faster? Why?, 2. Specific heat capacities of some substances are given in table 3.2. Based on this table,, answer the following question:, i., , Write the difference between temperature and heat., , ii. Compare the heat-absorbing ability of metals: Aluminium and Copper, iii. If the same amount of water is taken in a copper vessel and iron vessel and give it, the same amount of heat. Which will boil first?, iv. The same amount of recently prepared food is taken in Aluminium, vessel, and, Copper vessel. Which will be fresher after 4 hours?, , State Institute of Technical Teachers’ Training & Research, , |, , Page, , 92

Page 105 :
Applied Physics - !, , Application of specific heat capacity in daily life are:, a) Substances having a small specific heat capacity can be quickly heated up to a higher, temperature even though only a small amount of heat is supplied. Such materials are very, useful in making cookware such as frying pans, pots, kettles, etc., b) Sensitive thermometers also must be made from materials with small specific heat, capacity so that they can detect and show a change in temperature quickly., c) Substances that have a high specific heat capacity are suitable as a material for, constructing kettle handlers, insulators, and oven covers because a high amount of heat, will cause only a small change in temperature and the material won't get hot too fast., d) Heat storage instruments are usually made of substances with a high specific heat, capacity., e) Water acts as an excellent cooling agent in engines due to its high specific heat capacity., f) Water is also used in houses in cold climate countries because as it is heated up (boiled),, it tends to retain heat and warm the house due to its high specific heat capacity., , State Institute of Technical Teachers’ Training & Research, , |, , Page, , 93

Page 106 :
Applied Physics - !, , PRACTICE PROBLEMS, 1., , A man catches a ball of mass 1kg moving with a velocity of 20 m/s. Find the work done., (Ans: 200 J), , 2., , Calculate the kinetic energy of abody of mass 2 kg and momentum 100 kg m/s. (Ans: 2500, J), , 3., , An engine pumps 100 kg of water through a height of 10 m in 5 s. If the efficiency of the, engine is 60%, what is the power of the engine? (Ans: 3267 W), , 4., , A stone of mass 0.5 kg is thrown vertically upwards with a velocity120 m/s. Calculate its, kinetic energy at the end of 3 s. (Ans: 2052 J), , 5., , Two bodies of mass 1 kg and 4 kg have equal linear momenta. What is the ratio of their, kinetic energies? (Ans: 4:1), , 6., , A vehicle of mass 15 quintal climbs up a hill 230 m high. It then moves on a level road with, a speed of 30 m/s. Calculate the potential energy gained by it and its total mechanical, energy while running on the top of the hill. (Ans: 4.056 x 10 6 J), , 7., , Show that the temperature -40 0C is unique in numerical value on both Celsius and, Fahrenheit scales of temperatures., , 8., , On the Fahrenheitscale, what is the value of absolute zero? (Ans: -459.67 o F), , 9., , A patient’s temperature changed between 96.8 0F and 105.8 0F during a course of illness., Find the temperature range recorded on the Celsius scale. (Ans: 36, 41), , 10. If the change of temperature of a body is 20 0C, Find the change of temperature of the body, in the Fahrenheit scale. (Ans: a change of 36 0F), , State Institute of Technical Teachers’ Training & Research, , |, , Page, , 94

Page 107 :
Applied Physics - !, , QUESTIONS, 1., , What is work?, , 2., , Define energy., , 3., , Write different forms of energy., , 4., , What is energy transformation?, , 5., , What is mechanical energy?, , 6., , State law of conservation of energy., , 7., , Define the unit of work., , 8., , State mathematical expression of work., , 9., , Write two examples wherethe force acting on a body does no work?, , 10. Explain why the work and energy have the same unit., 11. Match the statements in column A, with those in column B, Column A, , Column B, , 1., , Ability to do work, , a), , Solar cells, , 2., , Unit of energy, , b), , Energy, , 3., , Transformation of energy, , c), , Mechanical energy, , 4., , Kinetic energy, , d), , Calorie, , 12. Two bodies of mass m1 and m2 have the same linear momentum. What is the ratio of their, kinetic energies? (Ans: K1/K2 = m2/m1), 13. If the kinetic energies of two bodies of mass m1 and m2 are the same, what is the ratio of, their momenta? (Ans:, , ), , 14. Match the statements in column A, with those in column B, Column A, , Column B, , Photosynthesis, , Electric energy to sound energy, , Loudspeaker, , Muscular energy to potential energy, , Lighting of bulb, , Light energy tochemical energy, , Wind a watch, , Electric energy to heat energy, , State Institute of Technical Teachers’ Training & Research, , |, , Page, , 95

Page 108 :
Applied Physics - !, , 15. Describe how the sun is the ultimate source of energy., 16. Differentiate the process of conduction, convection, and radiation., 17. Differentiate heat and temperature., 18. Briefly explain the working of a pyrometer., 19. Explain different temperature scales., 20. What do you mean by specific heat capacity?, 21. Match the statements in column A, with those in column B, Column A, 1., , Winds, , Column B, a), , Measure temperature without, touching the body, , 2., , Good conductor, , b), , Liquid thermometer, , 3., , Pyrometer, , c), , Convection, , 4., , Mercury thermometer, , d), , Silver, , 22. The temperature of the body gets considerably lowered when one puts on wet clothes. Why?, 23. Thermometer A is more sensitive than thermometer B. Comment on the statement., 24. A thermometer bulb should have a high heat capacity. Is the statement true? Justify your, answer., , State Institute of Technical Teachers’ Training & Research, , |, , Page, , 96

Page 109 :
Applied Physics - !, , CHAPTER 4, PROPERTIES OF MATTER, Conceptual Learning 4.1, Classify the following materials into groups having common properties. List out the common, properties of each group., a) Aluminium, b) Water, c) Gold, d) Coir, e) Twine, f) Oxygen, g) Air, h) Rubber, i) Kerosene, j) Coconut oil, k) Carbon dioxide, , The universe consists of matter and energy. Generally, the matter is defined as the thing, which needs a volume to occupy. Consider an ice cube, a cup of water, and water vapor – at the, molecular level each one is the same, H2O, but at different states of matter, they have specific, properties. Then we must learn the different properties of matter so that we can find applications, of materials to make our life easier than it is. In this chapter, we are going to deal with some of, the properties of matter such as elasticity, viscosity, surface tension, etc., , State Institute of Technical Teachers’ Training & Research, , |, , Page, , 97

Page 110 :
Applied Physics - !, , 4.1 ELASTICITY, We know that the stable states of matter are solid, liquid and gas. Besides these, there are, plasma, Bose-Einstein condensate, fermionic condensate, gluon plasma, etc. which exist under, special environmental conditions such as pressure, temperature, etc. In this section, we are going, to discuss elasticity which is a property of solids. Elasticity is an important property of materials, in our day-to-day life as the world emerging with material science. Starting from the, nanomaterial to the construction of bridges and buildings, continuously moving mechanical parts, of machine or engine – knowing the elasticity property of solids used is salient and vital., Take a rubber band with a known length, stretch it longitudinally by applying a, (moderate) force with both of your hands. The rubber band will undergo elongation. After, removing the applied force, the rubber band retains its original dimension. The force we applied, to deform the material is called deforming force. What we see is, some solid materials undergo, deformation under applied force and retain its original shape after removing the applied force., The property of solids to retain its original size or shape after the removal of deforming force is, called elasticity. The materials with the elastic property are called elastic materials. Quartz,, Phosphor bronze (an alloy of phosphor and bronze), steel, glass, ivory, are perfectly elastic, bodies., Some materials remain in the deformed state without showing any tendency to regain its, original size or shape when the applied force is removed. The property of a material to undergo, permanent deformation under applied force is called plasticity. Materials showing plastic, behaviour are called plastic materials. Clay, mud, plaster of Paris, etc. are examples of plastic, materials., If we keep the rubber band in a stretched state for some time, we feel some pain in our, hands. That is there is a counterforce against the applied force developed internally in our rubber, material to retain its original dimension. So, elasticity can otherwise understand as the ability of, some solid material to generate internal force against the deformation force applied externally., The internal reaction force developed inside an elastic material to resist any change in its size or, shape is called restoring force. To study the elasticity of solids, we need to define two terms, stress and strain., State Institute of Technical Teachers’ Training & Research, , |, , Page, , 98

Page 111 :
Applied Physics - !, , 4.1.1 Stress, Stress is defined as the internal restoring force developed per unit area in a body when, deforming forces are applied to it. For an elastic body, restoring force is always equal to the, applied force. Hence, stress can also be defined as the force per unit area applied to a material., 𝑆𝑡𝑟𝑒𝑠𝑠 =, , 𝐹𝑜𝑟𝑐𝑒, 𝐹, =, 𝐴𝑟𝑒𝑎, 𝐴, , The SI unit of stress is N/m2or pascal., , 4.1.2 Strain, Strain is defined as the ratio of change in dimension to the original dimension of a body., It is a measure of deformation produced in a body under the action of deforming forces., 𝑆𝑡𝑟𝑎𝑖𝑛 =, , 𝐶ℎ𝑎𝑛𝑔𝑒 𝑖𝑛 𝑑𝑖𝑚𝑒𝑛𝑠𝑖𝑜𝑛, 𝑂𝑟𝑖𝑔𝑖𝑛𝑎𝑙 𝑑𝑖𝑚𝑒𝑛𝑠𝑖𝑜𝑛, , The strain has no unit since it is the ratio of the same physical quantity., The important thing to understand is that we can define or calculate the term stress before, the material is elastically deformed, but the strain is defined only after deformation., , 4.1.3 Elastic limit, Elastic materials retain its elastic property up to a limit of the applied stress. The elastic, limit of a substance is defined as the maximum stress that can be applied to the substance before, it becomes permanently deformed and does not return to its original state. Material is elastic, when the stress is below its elastic limit and becomes plastic if stress is above the elastic limit., , 4.1.4 Hooke’s Law, English Scientist Robert Hooke in 1660 deduced a law about the elasticity of solids under, relatively small deforming forces. Hooke’s Law states that the stress is proportional to the, strain, within the elastic limit., 𝑠𝑡𝑟𝑒𝑠𝑠 ∝ 𝑠𝑡𝑟𝑎𝑖𝑛, State Institute of Technical Teachers’ Training & Research, , |, , Page, , 99

Page 112 :
Applied Physics - !, , 𝑠𝑡𝑟𝑒𝑠𝑠, = 𝑎 𝑐𝑜𝑛𝑠𝑡𝑎𝑛𝑡, 𝑠𝑡𝑟𝑎𝑖𝑛, The constant of proportionality depends on the material being deformed and on the nature, of the deformation and it is called as modulus of elasticity or elastic modulus. Since strain is a, pure number, the unit of elastic modulus is the same as that of stressi.e., N/m 2 or pascal., , 4.1.5 Young’s Modulus: Elasticity of Length, Consider a long bar of cross-sectional area A and initial length L that is clamped at one, end. When an external force is applied perpendicular to the cross-section, internal forces in the, bar resist distortion (“stretching”), but the bar reaches an equilibrium situation in which its final, length Lf, which is greater than L and in which the external force is exactly balanced by internal, forces. In such a situation, the bar is said to be stressed. We define longitudinal stress as the ratio, of the magnitude of the external force F to the cross-sectional area A., 𝐿𝑜𝑛𝑔𝑖𝑡𝑢𝑑𝑖𝑛𝑎𝑙 𝑠𝑡𝑟𝑒𝑠𝑠 =, , 𝐹, 𝐴, , The longitudinal strain is defined as the ratio of the change in length ΔL to the original, length L. Strain can be tensile (increase in length) or compressive (decrease in length)., 𝐿𝑜𝑛𝑔𝑖𝑡𝑢𝑑𝑖𝑛𝑎𝑙 𝑠𝑡𝑟𝑎𝑖𝑛 =, , ∆𝐿, 𝐿, , Young’s modulus (Y) is a measure of the length elasticity of a material. Young’s Modulus, is defined as the ratio of longitudinal stress to the longitudinal strain under relatively small, deforming force., 𝑌𝑜𝑢𝑛𝑔 𝑠 𝑀𝑜𝑑𝑢𝑙𝑢𝑠 =, , 𝐿𝑜𝑛𝑔𝑖𝑡𝑢𝑑𝑖𝑛𝑎𝑙 𝑠𝑡𝑟𝑒𝑠𝑠, 𝐿𝑜𝑛𝑔𝑖𝑡𝑢𝑑𝑖𝑛𝑎𝑙 𝑠𝑡𝑟𝑎𝑖𝑛, , 𝐹, 𝑌= 𝐴, ∆𝐿, 𝐿, 𝐹𝐿, 𝑌=, 𝐴 ∆𝐿, , State Institute of Technical Teachers’ Training & Research, , |, , Page, , 100

Page 113 :
Applied Physics - !, , Conceptual Learning 4.2, Answer the following questions based on the table given below, , Material, , Youngs modulus, (×10 10 N/m2), , Steel, , 20.0, , Copper, , 11.0, , Brass, , 9.1, , Glass, , 5.5, , Rubber, , 0.05, , 1. Arrange the materials in the increasing order of their deformed length under unit, external force, consider that the materials given are having the same dimension before, deformation?, 2. Under a given external applied force, the glass and rubber show a 1 meter extension in, length. Which one would be thicker?, 3. Comment the following sentence A copper cable is cut into half of its original length., The maximum load it can support is the same as the previous load., 4. Which of the material given in the table is best to make springs?, , 4.1.6 Rigidity Modulus: Elasticity of Shape, Another type of deformation occurs when an object is subjected to a deforming force, parallel to one of its faces while the opposite face is held fixed by another force. Consider a book, with a considerable thickness (A dictionary or something), place it on a table and gently push, sidewise with your palm which is placed over the book. The rectangular or square box type book, now looks like a parallelogram box. The stress in this case is called shear stress. If the object is, originally a rectangular block, shear stress results in a shape whose cross-section is a, parallelogram. That is, we are deforming the shape of the object without changing its volume by, applying a parallel deforming force to one of the faces of the object. This is called shearing., State Institute of Technical Teachers’ Training & Research, , |, , Page, , 101

Page 114 :
Applied Physics - !, , Fig. 4.1 Shearing a rectangular block by applying a force parallel to one of its, faces, Shear stress is defined as the ratio of the tangential force (F) applied to the area (A) of the, face being sheared., 𝑠ℎ𝑒𝑎𝑟 𝑠𝑡𝑟𝑒𝑠𝑠 =, , 𝑡𝑎𝑛𝑔𝑒𝑛𝑡𝑖𝑎𝑙 𝑓𝑜𝑟𝑐𝑒, 𝐹, =, 𝑎𝑟𝑒𝑎, 𝐴, , Shear strain is defined as the ratio of horizontal distance (∆𝑥) that the sheared face moves to the, height (h) of the object., 𝑠ℎ𝑒𝑎𝑟 𝑠𝑡𝑟𝑎𝑖𝑛 =, , ∆𝑥, ℎ, , If the deformation is very small, the shear strain can be recognized by the angular, deformation (). From the figure, angular deformation in radian is, 𝜃=, , 𝑎𝑟𝑐 𝑙𝑒𝑛𝑔𝑡ℎ, ∆𝑥, =, 𝑟𝑎𝑑𝑖𝑢𝑠, ℎ, , ∴ 𝑠ℎ𝑒𝑎𝑟 𝑠𝑡𝑟𝑎𝑖𝑛 = 𝜃, Rigidity modulus or shear modulus () is defined as the ratio of shear stress to shear strain., 𝑅𝑖𝑔𝑖𝑑𝑖𝑡𝑦 𝑀𝑜𝑑𝑢𝑙𝑢𝑠 =, , State Institute of Technical Teachers’ Training & Research, , 𝑠ℎ𝑒𝑎𝑟 𝑠𝑡𝑟𝑒𝑠𝑠, 𝑠ℎ𝑒𝑎𝑟 𝑠𝑡𝑟𝑎𝑖𝑛, , |, , Page, , 102

Page 115 :
Applied Physics - !, , 𝐹, 𝜂= 𝐴, 𝜃, 𝐹, 𝜂=, 𝐴𝜃, , 4.1.7 Bulk Modulus: Volume Elasticity, Bulk modulus characterizes the response of an object to changes in a force of uniform, magnitude applied perpendicularly over the entire surface of the object. The stress is now a, uniform pressure on all sides, and the resulting deformation is a volume change. An object, subject to this type of deformation undergoes a change in volume. When we are blowing a, balloon with our mouth or some pump, the air we forcefully passing into the balloon pushes on, all surfaces uniformly such that the balloon changes its volume., We define volume stress as the ratio of the magnitude of the total force (F) exerted on a, surface to the area (A) of the surface. The perpendicular force per unit area is called pressure (P)., 𝑣𝑜𝑙𝑢𝑚𝑒 𝑠𝑡𝑟𝑒𝑠𝑠 =, , 𝐹, =𝑃, 𝐴, , Under pressure, the object experiences a volume change ΔV. The volume strain or bulk, strain is defined as the ratio of the change in volume to the original volume., 𝑣𝑜𝑙𝑢𝑚𝑒 𝑠𝑡𝑟𝑎𝑖𝑛 =, , ΔV, 𝑉, , Bulk modulus (B) is defined as the ratio of volume stress to volume strain., 𝑉𝑜𝑙𝑢𝑚𝑒 𝑠𝑡𝑟𝑒𝑠𝑠, 𝑉𝑜𝑙𝑢𝑚𝑒 𝑠𝑡𝑎𝑖𝑛, 𝑃, 𝐵= −, ΔV, 𝑉, 𝑃𝑉, 𝐵=−, Δ𝑉, , 𝐵𝑢𝑙𝑘 𝑀𝑜𝑑𝑢𝑙𝑢𝑠 =, , A negative sign is inserted in this defining equation so that B is a positive number. This, exercise is necessary because an increase in pressure (positive ΔP) causes a decrease in volume, (negative ΔV) and vice versa. The reciprocal of the bulk modulus is called the compressibility, and is denoted by 𝑘, , State Institute of Technical Teachers’ Training & Research, , |, , Page, , 103

Page 116 :
Applied Physics - !, , 𝑘=, , 1, Δ𝑉, =−, 𝐵, P𝑉, , The SI unit of compressibility is that of reciprocal of pressure,Pa -1. Materials with small, bulk modulus and large compressibility are easier to compress., , Conceptual Learning 4.3, The table below shows typical values of elastic moduli of a few substances., Substance, , Young’s Modulus, , Rigidity Modulus, , Bulk Modulus, , (×10 10 N/m2), , (×10 10 N/m2), , (×10 10 N/m2), , Tungsten, , 35, , 14, , 20, , Steel, , 20, , 8.4, , 6, , Copper, , 11, , 4.2, , 14, , Brass, , 9.1, , 3.5, , 6.1, , 7, , 2.5, , 7, , Glass, , 6.5-7.8, , 2.6-3.2, , 5-5.5, , Quartz, , 5.6, , 2.6, , 2.7, , Water, , -, , -, , 0.21, , Mercury, , -, , -, , 2.8, , Aluminium, , 1. Why there is no entry for Young’s Modulus and Rigidity Modulus of some substances?, 2. What is the specialty of such materials?, 3. Why there is a value for Bulk modulus for those substances?, , State Institute of Technical Teachers’ Training & Research, , |, , Page, , 104

Page 117 :
Applied Physics - !, , Example 4.1, A metal wire of length 5 m and diameter 2 mm is stretched by hanging a mass of 8 kg at one end, and keeping the other end fixed to a sealing. Find the extension produced if the Young’s, Modulus of the material of the wire is Y = 7 x 1010 N/m2?, Solution:, Diameter of the wire, d = 2 mm, Radius of the wire, r = d/2 = 2/2 = 1 mm = 0.001 m, Area of cross section of the wire,, 𝐴 = 𝜋𝑟 = 3.14 × (0. 001) = 3.14 × 10 𝑚, Length of the given wire L = 5 m, Young’s Modulus of the material of the wire, Y = 7 x 1010 N/m2, Mass suspended = 8 kg, Force due to the mass = mg = 8x9.8 = 78.4 N, We have, Young’s Modulus, 𝑌 =, , ∆, , 𝑚𝑔 𝐿, 𝜋𝑟 𝑌, 78.4 × 5, ∆𝐿 =, 3.14 × 10 × 7 × 10, ∴ ∆𝐿 =, , = 1.78 × 10 𝑚, , Example 4.2, A hydraulic press contains 0.5 m3 of oil. Find the decrease in the volume of the oil when it is, subjected to a pressure of 2.6x107 Pa. The bulk modulus of the oil is B = 5.0x109 Pa?, Solution:, Volume of the oil before hydraulic press = 0.5 m3, Pressure applied = 2.6x107 Pa, Bulk Modulus of the given oil, B = 5.0x109 Pa, Bulk modulus of substance, 𝐵 = −, , State Institute of Technical Teachers’ Training & Research, , ∆, , |, , = −, , ∆, , Page, , 105

Page 118 :
Applied Physics - !, , Change in volume, ∆𝑉 = −, , 𝑃𝑉, 𝐵, , ∆𝑉 = −, , 2.6 × 10 × 0.5, 5.0 × 10, , ∆𝑉 = −2.6 × 10 𝑚, Example 4.3, A solid brass sphere is initially surrounded by air, and the air pressure exerted on it is 1.5x10 5, N/m2 (normal atmospheric pressure). The sphere is lowered into the ocean to a depth where the, pressure is 2.8x107 N/m2. The volume of the sphere in the air is 0.85 m 3. By how much does this, volume change once the sphere is submerged? The bulk modulus of brass is 6.1x10 10N/m2., Solution:, Air pressure on the brass sphere = 1.5x105 N/m2, Pressure at the depth of ocean = 2.8x107 N/m2, Volume of brass sphere at air = 0.85 m3, Pressure on brass sphere when it is submerged = 2.8x107 - 1.5x105, Bulk modulus of substance,𝐵 = −, Change in volume, ∆𝑉 = −, ∆𝑉 = −, , ∆, , = −, , ∆, , 𝑃𝑉, 𝐵, , 0.85(2.8 × 10 − 1.5 × 10 ), 6.1 × 10, , ∆𝑉 = −3.88 × 10, , 𝑚, , Example 4.4, A square copper slab having a side of 75 cm and a thickness of 15 cm is subjected to a shearing, force of 12x104 N on the thickness-wise side. The lower edge is kept fixed to the floor. How, much will the upper edge be displaced or sheared? The rigidity modulus of copper is 4.2 ×, 10 N/m2., Solution:, The shearing force is applied parallel to the thickness wise face; hence it is, applied on an area of 75x15 cm2 = 1125 cm2 =0.1125 m2, State Institute of Technical Teachers’ Training & Research, , |, , Page, , 106

Page 120 :
Applied Physics - !, , Therefore, the radius of the cable, 𝑟 =, , =, , . ×, ., , = 1.73 × 10 𝑚, , Therefore, the required diameter of the cable, d = 2r = 3.46x10 -3m, , 4.2 PRESSURE, We know what happens to a man if an elephant steps on his chest. But in the circus, the, same act is performed with the help of a wooden plank. That means both the force and its, coverage area are important. The smaller the area on which the force acts, the greater is the, impact. To make use of this concept, we use the idea of pressure. Pressure (P) is defined as the, perpendicular or normal force acting per unit area of a substance., 𝑃𝑟𝑒𝑠𝑠𝑢𝑟𝑒 =, 𝑃 =, , 𝐹𝑜𝑟𝑐𝑒, 𝐴𝑟𝑒𝑎, , 𝐹, 𝐴, , SI unit of pressure is N/m2 or pascal (Pa). One pascal is the pressure exerted by a force of, 1 N on an area of 1 m2.Pascal is a very small unit of pressure. Other commonly used units for, pressure are 𝑏𝑎𝑟 = 10 𝑃𝑎 and 𝑚𝑖𝑙𝑙𝑖𝑏𝑎𝑟 = 100 𝑃𝑎., , Conceptual Learning 4.4, Which of the following exerts the most pressure while resting on a floor?, 1. A cubic box of weight 25 N and 1.5 m sides, 2. A cylinder of weight 15 N and a base radius of 1 m, 3. A cubic box of weight 25 N with 2m sides, 4. A cylinder of weight 25 N and a base radius of 1 m, , 4.2.1 Pressure inside a Fluid (Hydrostatic pressure), A fluid is any substance that flows or deforms under applied shear stress. Liquids and, gases are both fluids. Fluids do not sustain shearing stresses or tensile stresses, because it does, not have a definite size or shape. The shape or size of fluid is the same as that of the container of, the fluid. Therefore, the only stress that can be exerted on an object submerged in a static fluid is, State Institute of Technical Teachers’ Training & Research, , |, , Page, , 108

Page 121 :
Applied Physics - !, , one that tends to compress the object from all sides. The force exerted by a static fluid on an, object is always perpendicular to the surfaces of the object and this perpendicular force per unit, area is called hydrostatic pressure. Hydrostatic pressure is the pressure that is exerted by a fluid, at equilibrium at a given point within the fluid, due to the force of gravity or weight of the fluid., ℎ𝑦𝑑𝑟𝑜𝑠𝑡𝑎𝑡𝑖𝑐 𝑝𝑟𝑒𝑠𝑠𝑢𝑟𝑒 =, 𝑃=, , 𝐹𝑜𝑟𝑐𝑒 𝑖𝑛𝑠𝑖𝑑𝑒 𝑡ℎ𝑒 𝑓𝑙𝑢𝑖𝑑, 𝑎𝑟𝑒𝑎, , 𝐹, 𝐴, , Pressure is not a vector quantity. It acts in any direction with the same magnitude. That, is, it has no directional property. It is true that force acting on the surface is a vector quantity, but, the expression for pressure involves only the magnitude of force. And the value for pressure thus, obtained is independent of the orientation of the surface area., Pressure is the force per unit area acting normally to a surface element within a fluid. Due, to the high mobility of the molecules of the fluid, the force acting at one position propagates, immediately and isotropically with the same magnitude through the entire volume of the fluid., Within a fluid at rest, the normal force exerted on a small surface has the same magnitude, everywhere and is independent of the orientation of the surface. This fact is called Pascal's law., This is the basic principle behind hydraulic machines like a crane, break, lift, etc., , 4.2.2 Atmospheric Pressure (𝑷𝒂𝒕𝒎 ), We live at the bottom of an ocean of air called the atmosphere. Each body, every grain of, sand, any object situated on the Earth is subject to air pressure. Atmospheric pressure is not so, small. The cause of atmospheric pressure is obvious. Just as water, air possesses weight and,, therefore, exerts a pressure equal (just as for water) to the weight of the column of air above the, body. The atmospheric pressure decreases with an increase in altitude. The higher we climb up a, mountain, the lesser will be the air above us and therefore, the lower will be the atmospheric, pressure become. Mountaineers get bleed through their nose or ear due to this pressure, difference., The pressure of the atmosphere at any point is equal to the weight of a column of air of, unit cross-sectional area extending from that point to the top of the atmosphere. The atmosphere, State Institute of Technical Teachers’ Training & Research, , |, , Page, , 109

Page 122 :
Applied Physics - !, , of the earth is spread up to a height of 200 km. Atmospheric pressure can be measured with a, mercury barometer in which pressure is measured in terms of the height of the mercury (Hg), column. At sea level, atmospheric pressure corresponds to 76 cm of Hg which is equivalent to, 1.013 × 105 Pa. One atmosphere (atm) is a standard unit of pressure equal to the mean, atmospheric pressure at sea level., 1𝑎𝑡𝑚 = 1.013 × 10 𝑃𝑎 = 76 𝑐𝑚 𝑜𝑓 𝐻𝑔, , 4.2.3 Gauge Pressure and Absolute Pressure, You might have experienced the pressure exerted by water while playing in water bodies., As you move deep into the water, it pushes you up. The pressure inside the water increases with, depth. Likewise, atmospheric pressure decreases with increasing altitude (height from the earth's, surface); for this reason, aircraft flying at high altitudes must have pressurized cabins for the, comfort of the passengers., To find the pressure at a depth, consider a fluid at rest in a container. In Fig. 4.2, point 1, is at height h above point 2. The pressures at points 1 and 2 are P 1 and P2 respectively. Consider, a cylindrical element of fluid having base area A and height h. As the fluid is at rest the resultant, horizontal forces should be zero and, the resultant vertical forces should, balance the weight of the element., The forces (Remember, F=PA, since, pressure P=F/A) acting in the vertical, direction are due to the fluid pressure, at the top (P1A) acting downward, at, the bottom (𝑃 𝐴) acting upward., If mg is the weight of the fluid, in the cylinder, then, (𝑃 − 𝑃1)𝐴 = 𝑚𝑔, , Fig. 4.2Pressure inside a fluid at rest in a container, , Now, if ρ is the mass density of the fluid, we know that, State Institute of Technical Teachers’ Training & Research, , |, , Page, , 110

Page 123 :
Applied Physics - !, , 𝐷𝑒𝑛𝑠𝑖𝑡𝑦 (𝜌) =, , 𝑀𝑎𝑠𝑠, 𝑚, =, 𝑉𝑜𝑙𝑢𝑚𝑒 𝑉, , Therefore, the mass of fluid,, 𝑚 = 𝜌𝑉 = 𝜌ℎ𝐴, So, the above equation can rewrite as,, (𝑃 − 𝑃1)𝐴 = 𝜌ℎ𝐴𝑔, (𝑃 − 𝑃1) = 𝜌𝑔ℎ, That is, Pressure difference (P2 -P1) depends on the vertical distance h between the points, (1 and 2), the density of the fluid ρ, and acceleration due to gravity g., If point 1 under discussion is shifted to the top of the fluid (say water), which is open to, the atmosphere, P1 may be replaced by atmospheric pressure (𝑃, , ) and we replace P2 by P., , Then the above equation turns to, (𝑃 − 𝑃, , ) = 𝜌𝑔ℎ, , 𝑃=𝑃, , + 𝜌𝑔ℎ, , Thus, the pressure P, at depth below the surface of a liquid open to the atmosphere is, greater than atmospheric pressure by an amount 𝜌𝑔ℎ. This P is called absolute pressure at that, point. Absolute pressure at a point is pressure measured with respect to zero pressure or absolute, vacuum., The excess of pressure,(𝑃 − 𝑃, , ) at depth, h is called a gauge pressure at that point., , Gauge pressure at a point is the pressure measured relative to the atmospheric pressure. Bloodpressure readings, such as 130/80 mm of Hg, give the maximum and minimum gauge pressures, in the arteries, measured in mm Hg or torr. Blood pressure varies with vertical position within, the body; the standard reference point is the upper arm, level with the heart., , Conceptual Learning 4.5, The Mariana Trench, in the Pacific Ocean, is about 11.0 km deep. If the atmospheric pressure, at sea level is 1.01 x 105 Pa, how much pressure would a submarine need to be able to, withstand to reach this depth?, , State Institute of Technical Teachers’ Training & Research, , |, , Page, , 111

Page 124 :
Applied Physics - !, , Conceptual Learning 4.6, Calculate the depth in the ocean at which the pressure is three times atmospheric pressure?, , 4.3 SURFACE TENSION, An object less dense than water, such as an air-filled balloon, floats with part of its, volume below the surface. Conversely, a razor blade or a fine paper carefully placed over the, water surface can rest atop a water surface even though its density is several times that of water., This is an example of surface tension: The surface of the liquid behaves like a membrane under, tension., The surface of liquid acts in many respects in a manner analogous to a stretched, membrane. The careful examination of water drops slowly formed at the end of a glass tube or, tap from which it emerges provides another example of this phenomenon. The water in this case, accumulates as though it were collected in an invisible membrane, until of a definite size, when it, is detached as a spherical drop. These effects are due to forces existing on the surface of the, separation of liquid from the air and the other media in contact with it., Surface tension arises because, the molecules of the liquid exert, attractive forces on each other. There is, zero net force on a molecule inside the, volume of the liquid because it is, surrounded by molecules of the same, type from all sides. But a molecule at, the surface is pulled down by the, molecules of the liquid below it as, shown in Fig. 4.3. Surface molecules, can interact with air molecules above, , Fig. 4.3 Attractive forces on molecules in the bulk, and molecules at the surface of the liquid, , and the force exerted by air molecules is very small compared to the downward force exerted by, the molecules of the liquid. Due to the net downward force on the surface, the liquid tends to, minimize its surface area, just as a stretched membrane does. As liquids have no definite shape, State Institute of Technical Teachers’ Training & Research, , |, , Page, , 112

Page 125 :
Applied Physics - !, , but have a definite volume, they acquire a free surface when poured into a container. These, surfaces possess some additional energy. This phenomenon is known as surface tension and it is, concerned with only liquid as gases do not have free surfaces. Surface tension is the property of a, liquid surface to reduce its surface area to a minimum as possible due to the force exerted on, molecules of the surface by the molecules of the bulk. A sphere has a smaller surface area for its, volume than any other shape and that is why the freely falling raindrops are spherical in shape., Consider a line AB drawn on the surface of, the liquid as shown in the figure. The line divides the, surface into two parts. Since the liquid surface, behaves like a stretched membrane, the two parts of, the surface pull each other with a force that is, proportional to the length of the line AB. The forces, acting on the liquid surface are tangential to the, surface and are perpendicular to the line AB. If ‘F’ is, the magnitude of force acting perpendicular to the line, , Fig. 4.4 Surface of the liquid, acting, , AB of length ‘l’, then, 𝐹 ∝𝑙, 𝐹=𝑆𝑙, where the constant of proportionality ‘S’ is called surface tension., 𝑆=, , 𝐹, 𝑙, , Hence, surface tension can be defined as the force per unit length acting tangential to the surface, of the liquid to reduce the surface area of the liquid. The SI unit of Surface tension is N/m., , 4.3.1 Surface energy of the liquid, A molecule on the surface of the liquid has more potential energy than a molecule inside, the liquid. The extra energy possessed by the surface layer of the liquid is called surface energy, (U). Surface energy can be defined as the work done to increase the surface area of the liquid., Surface energy is related to surface tension by the equation,, State Institute of Technical Teachers’ Training & Research, , |, , Page, , 113

Page 126 :
Applied Physics - !, , 𝑠𝑢𝑟𝑓𝑎𝑐𝑒 𝑒𝑛𝑒𝑟𝑔𝑦 = 𝑠𝑢𝑟𝑎𝑓𝑐𝑒 𝑡𝑒𝑛𝑠𝑖𝑜𝑛 × 𝑎𝑟𝑒𝑎 𝑜𝑓 𝑡ℎ𝑒 𝑙𝑖𝑞𝑢𝑖𝑑 𝑠𝑢𝑟𝑓𝑎𝑐𝑒, 𝑈 =𝑆 ×𝐴, ∴ 𝑆=, , 𝑈, 𝐴, , Hence, surface tension can also be defined as the surface energy per unit area of the liquid, surface., , 4.3.2 Cohesion and Adhesion, The attractive forces of molecules are of two types- cohesion and adhesion. If the, molecules of the same kind attract, then it is called adhesion and if the molecules are of different, kinds attract, then it is called cohesion. Attractive forces acting between molecules of the same, kind are called cohesive forces. Attractive forces acting between molecules of different kinds are, called adhesive forces. Adhesion may occur between solid, liquid, or gaseous materials. When, aliquid comes in contact with a solid surface, the wetting of the surface occurs depending on the, ratio of strengths of cohesive and adhesive forces. When the adhesive forces dominate, the, surface tension of the liquid becomes low and the liquid spreads over the entire solid surface, (perfect wetting). When the cohesive forces dominate, the surface tension of the liquid becomes, high, and the liquid contracts into drops (no wetting)., , 4.3.3 Angle of contact, The surface of liquid near the plane of contact, with another medium, is in general, curved. The angle between the tangent to the liquid surface at the point of contact and the solid, surface inside the liquid is termed the angle of contact. It is denoted by θ. It is different at, interfaces of different pairs of liquids and solids. The value of θ determines whether a liquid will, spread on the surface of a solid or it will form droplets on it., , State Institute of Technical Teachers’ Training & Research, , |, , Page, , 114

Page 127 :
Applied Physics - !, , Fig. 4.5 Obtuse and acute angle of contacts at the solid -liquid interfaces, When θ is an obtuse angle, then the molecules of liquids are attracted strongly to, themselves and weakly to those of solid. The liquid does not wet the solid surface. It costs a lot, of energy to create a liquid-solid surface. This is what happens with water on a waxy or oily, surface, on the lotus leaf, and with mercury on any surface. If θ is an acute angle, the liquid, molecules are strongly attracted to those of the solid and the liquid gets easily wet to the solid, surface. This is what happens with water or kerosene on glass or plastic or any other surface., Water forms droplets on lotus leaves since they have large angles of contact. That is why, the lotus leaf is hydrophobic in nature. That means water drop has less contact area with the lotus, leaf surface. But for herbicides, the angle of contact with leaves should be small so that it would, have a larger contact area to leaf. That is, they should be hydrophilic in nature so that the, herbicides effectively act on the herb’s leaf and destroy it. Waterproofing agents or paints used, in buildings and other construction actually create a large angle of contact between the water and, fibers in it. So, the surface will become hydrophobic in nature., , State Institute of Technical Teachers’ Training & Research, , |, , Page, , 115

Page 128 :
Applied Physics - !, , 4.3.4 Capillarity, , Fig. 4.6 Capillary rise of water and capillary depression of, mercury, One of the consequences of surface tension is capillary action or capillarity. When one, end of a tube of very small radius (known as capillary tube) is dipped in a liquid, the liquid rises, or falls in the tube. This phenomenon is called capillarity. The rise or fall of liquid in the, capillary tube depends on the angle of contact between the liquid and the tube. If the angle of, contact is less than 90o (acute angle of contact), the liquid rises in the tube and it is called, capillary rise. If the angle of contact is greater than 90o (obtuse angle of contact), the liquid falls, in the tube and it is called capillary depression., , 4.3.5 Ascent Formula, The rising up of liquid through capillary tubes against gravity due to the surface tension, at the boundary line of the liquid and solid tube surface. The elevation height of liquid in a, capillary tube h is given by the ascent formula., h=, , 2𝑆 cos 𝜃, 𝑟𝜌𝑔, , Here S is the surface tension, θ is the angle of contact between the surface of the liquid and, surface of the capillary tube at the point of contact, r is the inner radius of the capillary tube, ρ is, State Institute of Technical Teachers’ Training & Research, , |, , Page, , 116

Page 129 :
Applied Physics - !, , the density of the liquid rising through the capillary tube and g is the acceleration due to gravity., From the expression, it is clear that for a given substance, the elevation depends only on the, radius of the capillary., , Conceptual Learning 4.7, Take three types of liquids, say water, kerosene, and mercury. Shall we observe the same, capillary rise with a capillary tube of the same diameter and orientation? If not, explain why, do they differ?, , 4.3.6 Applications of Surface Tension, a) The action of detergents on oil or grease dirt in fabrics, Washing with water does not remove the grease or oil stains. This is because the water, does not wet this dirt. That is there is the very little contact area between them. If water could, wet grease, the flow of water could carry some grease away. Something of this sort is achieved, through detergents. The molecules of detergents are hairpin-shaped, with one end attracted to, water and the other to molecules of grease, oil, or wax, thus tending to form water-oil interfaces., The addition of detergents, whose molecules attract at one end and say, oil on the other, reduces, drastically the surface tension S (water-oil). It may even become energetically favorable to form, such interfaces, i.e., globs of dirt surrounded by detergents and then by water. This kind of, process using surface-active detergents or surfactants is important not only for cleaning but also, in recovering oil, mineral ores, etc., b) Why do farmers plough the land in the summer season?, By the surface tension at the boundary line of the liquid, the liquid in very narrow tubes, rises despite gravity. This phenomenon of the rising of a liquid in a thin tube is called capillary, rise. In the summer season where water scarcity affects, the farmers plough the land to open up, the tiny capillary orifices between the soil. Through these capillaries, the water and air in the bed, will rise to the surface of the earth and keep the land living and organic., State Institute of Technical Teachers’ Training & Research, , |, , Page, , 117

Page 130 :
Applied Physics - !, , 4.3.7 Effect of temperature and impurities on surface tension, The surface tension of a liquid decreases with an increase in the temperature of the liquid., This is because cohesive forces decrease with an increase in molecular thermal activity. Hence, angle of contact also decreases with an increase in the temperature of the liquid. The surface, tension of the liquid increases with the concentration of dissolved impurities like common salt., For dissolved impurities, the surface tension increases linearly with the concentration of, dissolved material. The surface tension of the liquid decreases with insoluble impurities like oil,, grease, etc., , 4.4 FLUID DYNAMICS, Of the stable states of matter, liquids and gases can flow. So together they are called, fluids. Fluids are everywhere around us. Earth has an envelope of air and two-thirds of its surface, is covered with water. Water is essential for the existence of life on earth and our body is mainly, constituted of water. In this section, we are going to study the dynamics of fluids. An ideal fluid, is a fluid that is incompressible (that is, its density cannot change) and has no internal friction, (called non-viscous). Liquids are approximately incompressible in most situations, and we may, also treat gas as incompressible if the pressure differences from one region to another are not too, great., , 4.4.1 Streamline flow and turbulent flow, Generally, we are considering the fluid motion as layers, in each layer the fluid particles, are moving one by one in a line, called streamline or flow line. The flow is said to be steady, or, laminar if each particle of the fluid follows a smooth path such that the paths of different, particles never cross each other. That is the streamlines do not cross. In steady flow, every fluid, particle arriving at a given point has the same velocity irrespective of time. This does not mean, that the velocity at different points in space is the same. The velocity of a particular particle may, change as it moves from one point to another. That is, at some other point the particle may have, a different velocity, but every other particle which passes the second point behaves exactly like, the previous particle that has just passed that point. The object to be noted is that all the fluid, State Institute of Technical Teachers’ Training & Research, , |, , Page, , 118

Page 131 :
Applied Physics - !, , particles have a fixed value of the velocity at a particular point in the flow on arriving at that, point. This condition enforces the one-by-one streamline motion of fluid particles, that do not, cross., If the streamlines or flow lines are crossing, there must be multiple velocities for fluid, particles at that crossing point. This type of fluid flow is not steady or laminar, it is called, turbulent flow. Above a certain critical speed, the streamline fluid flow becomes turbulent., Turbulent flow is an irregular flow characterized by small whirlpool-like regions., The turbulent flow is mathematically difficult to handle. So, we are limiting our, discussions to the steady or laminar flow of fluid. Laminar flow is ideal, the flow of water, around us is somewhat turbulent in nature. As of now, consider the flow of water from a tap., Initially, there will be a very smooth flow of water when we gently try to open a tap, this smooth, flow can be treated as a streamline flow of fluid. And the steady smooth flow is getting narrower, as the distance from the opening of the tap increases and at last, the flow becomes irregular or, turbulent. How it is like this. We are going to learn here., Table 4.1: Comparison of streamline flow and turbulent flow of fluids, Streamline flow, , Turbulent flow, , It is the steady, smooth, regular, one-by-one The flow of particles is irregular and in a, flow of fluid particles., zigzag manner., The speed of fluid motion is lower than the The fluid motion speed is greater than the, critical velocity. Critical velocity of fluids is critical velocity., the velocity above which the flow becomes, irregular or turbulent., The fluid layers do not cross each other, , The fluid layer may cross each other, , The particles reaching a given point in the path, of flow have the same velocity with time. That, means a single velocity of particles is possible, at a given point in the flow of fluids., , The particles in the fluid can have different, velocities at a given point in the fluid flow., That means multiple velocities at a given, point in the flow can be possible., , State Institute of Technical Teachers’ Training & Research, , |, , Page, , 119

Page 132 :
Applied Physics - !, , 4.4.2 Reynold’s Number, For simplicity in handling, we took the ideal fluid which is incompressible and nonviscus. But practically the fluid is somewhat incompressible up to an extent, but it will have, some internal force between the fluid layers against the flow. Hence, we cannot neglect the, viscosity of the fluid. Osborne Reynolds (1842-1912) observed that turbulent flow is less, probable for viscous fluid flowing at low rates through a pipe. He defined a dimensionless, number that has a vital role in predicting whether a liquid has stream line flow or turbulent flow., This number is called the Reynolds number (R e).Reynolds number is defined as the ratio of, inertial forces to viscous forces within flowing fluid., 𝑖𝑛𝑒𝑟𝑡𝑖𝑎𝑙 𝑓𝑜𝑟𝑐𝑒, 𝑣𝑖𝑠𝑐𝑜𝑢𝑠 𝑓𝑜𝑟𝑐𝑒, , 𝑅 =, , 𝑅 =, , ρvd, η, , where ρ is the density of the fluid flowing with a speed v, d is the diameter of the pipe, and η is, the coefficient of viscosity of the fluid. It is found that flow is streamline or laminar for Re less, than 1000.The flow becomes unsteady for Re between 1000 and 2000.The flow is turbulent for, Re greater than 2000., , 4.4.3 Continuity Equation in Fluid Dynamics, At home, you are watering the garden with a hose connected to a water tank. And you, found a plant some distance away that your, hose cannot extend up to there. What will you, do? You may partially close the end of the, hose with your thumb such that the water, stream reaches there. What is happening here, is the application of the continuity equation., The eequation of continuity in fluid, dynamics is analogous to the law of, conservation mass in mechanics. Consider a, , Fig. 4.7 A pipe of non-uniform cross section, , State Institute of Technical Teachers’ Training & Research, , |, , Page, , 120

Page 133 :
Applied Physics - !, , pipe of varying cross-sectional area as shown in Fig.4.7, through which an incompressible and, non-viscous fluid flows. At the point P, let the velocity of the fluid be 𝑣 and area of crosssection be 𝐴 . At the point Q, let the velocity of the fluid be 𝑣 and area of cross-section be 𝐴 ., If 𝜌 is the density of the fluid and considering the flow of fluid through the pipe for a time ∆𝑡, we, can write, Distance travelled by the fluid at point P = 𝑣 ∆𝑡, The volume of the fluid entering the tube at P = 𝐴 𝑣 ∆𝑡, Mass of the fluid entering the tube at point P = 𝜌 𝐴 𝑣 ∆𝑡, Similarly,, Mass of the fluid entering the tube at point Q = 𝜌 𝐴 𝑣 ∆𝑡, The total mass of the fluid entering into a pipe through any cross-section should be equal to the, total mass of fluid coming out of the same pipe through any other cross-section at the same time., Therefore,, 𝜌 𝐴 𝑣 ∆𝑡 = 𝜌 𝐴 𝑣 ∆𝑡, 𝐴 𝑣 = 𝐴 𝑣, 𝐴𝑣 = 𝑐𝑜𝑛𝑠𝑡𝑎𝑛𝑡, Equation of continuity in fluid dynamics states that when an incompressible and nonviscous fluid moving with steady flow through a pipe of varying cross-sectional area, the product, of the area of cross-section and velocity of flow remains a constant at every point in the pipe., That means, where the area decreases, the velocity of fluid flow must be increased to maintain, the constant and vice versa. The product Av, which has the dimensions of volume per unit time,, is called either the volume flux or the flow rate. The condition Av = constant is equivalent to the, statement that the volume of fluid that enters one end of a tube in a given time interval equals the, volume leaving the other end of the tube in the same time interval if no leaks are present., You had reduced the cross-section area of the hose with your thumb, then according to, the continuity equation, the velocity of fluid flow must increase to keep the product constant. So,, the water stream flows with more speed and covers more distance. The steady smooth flow from, a tap, when we gently open it is getting narrower as the distance passes. Because of gravity, the, water starting from the tap gets accelerated and attains more velocity. By continuity equation in, fluid dynamics, as the velocity increases, the area of the cross-section must be reduced., State Institute of Technical Teachers’ Training & Research, , |, , Page, , 121

Page 134 :
Applied Physics - !, , Therefore, the steady smooth flow gets narrower as the distance from the tap increases. If the, velocity is further increasing beyond the critical velocity, the flow becomes irregular or, turbulent., , Conceptual Learning 4.8, The time required to fill a bucket with water from a certain garden hose is 30 s. If you cover, part of the hose’s nozzle with your thumb so that the speed of the water leaving the nozzle, doubles, how long does it take to fill the bucket?, , Example 4.6, The radius of a pipe decreases from 5 cm to 3 cm. If the velocity of water at the wider portion is, 7 m/s, calculate the velocity in the narrow portion?, Solution:, The radius of the pipe at the wider portion, 𝑟 = 5 cm = 5 x 10-2 m, Area of the cross-section at the wider portion, A1 = 𝜋𝑟, = 3.14 x (5 x 10-2)2 = 7.85 x 10-3 m2, Radius of the narrow portion, 𝑟 = 3 cm = 3 x 10-2 m, Area of cross section at narrow portion, A2 = 𝜋𝑟, , = 3.14x(3 x 10-2)2 = 2.826 x 10-3 m2, , According to continuity equation in fluid dynamics, A1v1 = A2v2, Velocity at the wider portion, 𝑣 = 7 m/s, Therefore, velocity at the narrow portion, 𝑣 =, , =, , ., , ×, ., , ×, ×, , 𝑣 = 19.44 𝑚/𝑠, Example 4.7, The diameter of a water pipe decreases from 15 cm to 7 cm. If the velocity at the wider portion is, 5 m/s. Calculate the velocity at the narrow region?, Solution:, Diameter of the pipe at wider portion d1 = 15 cm, The radius of the pipe at the wider portion, 𝑟 = d1/2 = 7.5 cm = 7.5 x 10-2m, , State Institute of Technical Teachers’ Training & Research, , |, , Page, , 122

Page 135 :
Applied Physics - !, , Area of the cross-section at the wider portion, A1 = 𝜋𝑟 = 3.14 x (7.5 x 10-2)2= 1.77 x 102, , m2, , Diameter of the pipe at the narrow portion, d 2 = 7 cm, The radius of the narrow portion, 𝑟 = d2/2 = 3.5 cm = 3.5 x 10-2m, Area of cross section at narrow portion, A2 = 𝜋𝑟, , = 3.14 x (3.5 x 10-2)2= 3.85 x 10-3 m2, , According to the continuity equation in fluid dynamics, 𝐴 𝑣 = 𝐴 𝑣, Velocity at the wider portion, 𝑣 = 5 m/s, Therefore, velocity at the narrow portion, 𝑣 =, , =, , ., , ×, ., , ×, , ×, , 𝑣 = 22.98 𝑚/𝑠, Example 4.8, Water flowing through a garden hose of diameter 4 cm fills a 50L pond in 35 seconds. What is, the speed of the water leaving the end of the hose?, Solution:, Diameter of the hose d = 4 cm, Radius of the hose r = d/2 = 4/2 = 2 cm = 2 x 10 -2m, Cross sectional area of the hose A = πr2 = 3.14 x 0.022 = 1.256 x 10-3 m2, Rate of flow or volume flow rate of water through the hose, ×, , =, , =, , 𝑚 /𝑠, , The continuity equation can be written as Av = a constant, The constant term is the rate of flow., That is, 𝐴𝑣 = 𝑟𝑎𝑡𝑒 𝑜𝑓 𝑓𝑙𝑜𝑤 𝑜𝑟 𝑣𝑜𝑙𝑢𝑚𝑒 𝑓𝑙𝑜𝑤 𝑟𝑎𝑡𝑒, Therefore, the velocity of water at the end of the hose, 𝑣 =, 𝑣=, , 1.43 × 10, 1.256 × 10, , = 1.14 𝑚⁄𝑠, , Example 4.9, Find out the velocity of water, if we connect a nozzle of diameter 2 cm at the end of the hose in, the above problem?, Solution:, Diameter of the nozzle connected to the hose = 2 cm, State Institute of Technical Teachers’ Training & Research, , |, , Page, , 123

Page 136 :
Applied Physics - !, , The radius of the nozzle connected to the hose = 1 cm = 1 x 10-2m, 𝐶𝑟𝑜𝑠𝑠 𝑠𝑒𝑐𝑡𝑖𝑜𝑛𝑎𝑙 𝑎𝑟𝑒𝑎 𝑜𝑓 𝑡ℎ𝑒 𝑒𝑛𝑑 𝑜𝑓 𝑡ℎ𝑒 ℎ𝑜𝑠𝑒 𝑜𝑟 𝑛𝑜𝑧𝑧𝑙𝑒 = 𝜋𝑟 = 3.14 ×. 01, 𝐴 = 3.14 × 10 𝑚, We have, 𝐴𝑣 = 𝑟𝑎𝑡𝑒 𝑜𝑓 𝑓𝑙𝑜𝑤 𝑜𝑟 𝑣𝑜𝑙𝑢𝑚𝑒 𝑓𝑙𝑜𝑤 𝑟𝑎𝑡𝑒, That is, speed of the water at the end of nozzle 𝑣 =, 𝑣=, , 1.43 × 10, 3.14 × 10, , = 4.55 𝑚/𝑠, , This problem can otherwise solve by the form of continuity equation in fluid, dynamics as, 𝐴 𝑣 =𝐴 𝑣, The cross-sectional area of the hose, A1 = 1.256 x 10-3 m2 (calculated in the above, problem), Speed of water from the hose,𝑣 = 1.14 m/s, , (calculated, , in, , the, , above, , problem), Cross sectional area of the nozzle A2 = 3.14 × 10 𝑚, Speed of water from the nozzle,𝑣 =?, Rearranging the continuity equation, we can have, 𝑣 =, 𝑣 =, , 1.256 × 10 × 1.14, = 4.56 𝑚/𝑠, 3.14 × 10, , Example 4.10, An incompressible oil of density 850 kg/m3 is pumped through a cylindrical pipe of differential, cross-section at a rate of 10 litres per second. The first section of the pipe has a diameter of 8.0, cm. The second section of the pipe has a diameter of 4.0 cm. (a) What are the flow speed and, mass flow rate in the first section? (b) What are the flow speed and mass flow rate in the second, section?, Solution:, Volume flow rate through the pipe = 10 litres per second = 10 x 10 -3 m3/s = 10-2m3/s, Diameter of the first section of the pipe d1 = 8 cm, The radius of the first section of the pipe, 𝑟 = d1/2 = 8/2 = 4 cm = 4 x 10-2m, State Institute of Technical Teachers’ Training & Research, , |, , Page, , 124

Page 137 :
Applied Physics - !, , Area of cross section of the first section, 𝐴 = 𝜋𝑟, 𝐴 = 3.14 × (4 × 10 ) = 5.024 × 10 𝑚, By continuity equation, 𝐴𝑣 = 𝑎 𝑐𝑜𝑛𝑠𝑡𝑎𝑛𝑡 = 𝑣𝑜𝑙𝑢𝑚𝑒 𝑓𝑙𝑜𝑤 𝑟𝑎𝑡𝑒, That is speed oil at the first section, 𝑣 =, 𝑣 =, , 10, 5.024 × 10, , = 1.99 𝑚/𝑠, , Diameter of the second section of the pipe d2 = 4 cm, The radius of the second section of the pipe, 𝑟 = d2/2 = 4/2 = 2 cm = 2 x 10-2m, Area of cross section of the second section, 𝐴 = 𝜋𝑟, , = 3.14 × (2 × 10 ), , A2 = 1.256 x 10-3 m2, Continuity equation in fluid mechanics otherwise expressed as, 𝐴1𝑣1 = 𝐴2𝑣2 = 𝑎 𝑐𝑜𝑛𝑠𝑡𝑎𝑛𝑡 = 𝑣𝑜𝑙𝑢𝑚𝑒 𝑓𝑙𝑜𝑤 𝑟𝑎𝑡𝑒, Therefore,, , 𝑣 =, , Or, , 𝑣 =, , =, , ., , ×, ., , × ., ×, , =, , = 7.96 𝑚/𝑠, , ., , ×, , = 7.96 𝑚/𝑠, , Mass flow rate and volume flow rate are constant since we are considering the flow of, fluid as streamline flow or laminar flow., Therefore, the mass flow rate at any point in the pipe = density of oil x volume flow rate, = 850 kg/m3 x 10-2 m3/s, = 8.5 kg/s, , 4.4.4 Energies of a flowing fluid, A flowing fluid possesses three types of energies – kinetic energy, potential energy, and, pressure energy., a) Kinetic energy, The kinetic energy is due to the motion of fluid particles. To understand this, let us put a, small leaf at the river on the coast side and then put the same leaf in the middle of the river. And, observe, which one is moving slow and fast? The leaf at the coast side moves slowly because the, water at the coast side moves slowly, but the leaf in the middle of the river moves faster because, State Institute of Technical Teachers’ Training & Research, , |, , Page, , 125

Page 138 :
Applied Physics - !, , the river moves fast in the middle. That is the motion of the fluid gives energy termed as kinetic, energy of fluids. If m mass of the fluid flows with a velocity v, then kinetic energy is given by, 𝐾𝑖𝑛𝑒𝑡𝑖𝑐 𝐸𝑛𝑒𝑟𝑔𝑦 =, , 1, 𝑚𝑣, 2, , For unit volume, we can rewrite this equation with the density of fluid ρ as, 𝐾𝑖𝑛𝑒𝑡𝑖𝑐 𝐸𝑛𝑒𝑟𝑔𝑦 =, , 1, 𝜌𝑣, 2, , b) Potential energy, The energy of the fluid by virtue of its position is called potential energy. To identify this, energy of fluid, pour a bucket of water at an herb planted on a pot in the courtyard, so far nothing, abnormal. Pour the same amount of water with the same bucket from the terrace to the herb in, the courtyard. What will happen? The herb and the pot may get damaged due to water from the, terrace. We had poured the same amount of water as we did from the courtyard, but with a new, position with some height. That means the height of the fluid can do some work, which means it, has extra energy due to its position. That energy is termed the potential energy of the fluid., 𝑃𝑜𝑡𝑒𝑛𝑡𝑖𝑎𝑙 𝐸𝑛𝑒𝑟𝑔𝑦 = 𝑚𝑔ℎ, In terms of density of fluid,, 𝑃𝑜𝑡𝑒𝑛𝑡𝑖𝑎𝑙 𝐸𝑛𝑒𝑟𝑔𝑦 = 𝜌𝑔ℎ, c) Pressure energy, Unlike in mechanics, a new kind of energy can be assessed to fluid, called pressure, energy due to the action of fluid molecules to any substance immersed. To recognize this energy,, remember, in childhood, we all were playing with our friends in pound or river. Throw up our, friends from the deep water to air, then up to water level from the deep we may not feel the, weight of our friend, when we reach just above water level can feel the weight of friend. Or, when we try to get water from a well, we may not feel the weight of the water can when it is, immersed in water, and we will feel the complete weight when the water can is just above the, water level. What is happening? when it is immersed in water, we do not feel the weight of the, object. That is someone is carrying it for us inside the water. That is fluid doing work. The object, immersed in water senses the forces from the fluid molecules. Since the fluid molecules applying, the force from all the sides, the net force is called pressure. This pressure is applied by the fluid, State Institute of Technical Teachers’ Training & Research, , |, , Page, , 126

Page 139 :
Applied Physics - !, , molecules doing work to carry the object for us underwater. So, the fluid is doing work and we, can say it possesses energy. That is pressure energy. If P is the pressure, m is the mass of fluid, and ρ is the density of the fluid, the pressure energy is given by, 𝑃𝑟𝑒𝑠𝑠𝑢𝑟𝑒 𝐸𝑛𝑒𝑟𝑔𝑦 =, , 𝑚𝑃, 𝜌, , For unit volume, we can rewrite this equation as, 𝑃𝑟𝑒𝑠𝑠𝑢𝑟𝑒 𝐸𝑛𝑒𝑟𝑔𝑦 = 𝑃, , 4.4.5 Bernoulli’s Theorem, According to the continuity equation, the speed of fluid flow can vary along the paths of, the fluid. What about pressure? The variation of pressure of flowing fluid depends on height as, in the static situation and it also depends on the speed of flow. We can derive an important, relationship called Bernoulli’s equation that relates the pressure, flow speed, and height for the, flow of an ideal fluid. Bernoulli’s equation is an essential tool in analyzing plumbing systems,, hydroelectric generating stations, and the flight of airplanes., Bernoulli’s equation is a general expression that relates the pressure difference between, two points in the pipe to both velocity changes (kinetic energy change) and elevation (height), changes (potential energy change). Bernoulli’s theorem is analogous to the law of conservation, of energy in Mechanics and is derived by applying the work-energy theorem to the fluid in a, section of a flow tube. By work-energy theorem at two sections of a pipe with different heights, h1 and h2 and v1 and v2 are the velocities of flow with pressure P 1 and P2. we can write,, (𝑃2 − 𝑃1)𝑉 =, , 1, 1, 𝑚𝑣 − 𝑚𝑣 + 𝑚𝑔ℎ + 𝑚𝑔ℎ, 2, 2, , .𝑃 − 𝑃 = 𝜌𝑣 − 𝜌𝑣 + 𝜌𝑔ℎ − 𝜌𝑔ℎ, 1, 1, 𝑃 + 𝜌𝑣 + 𝜌𝑔ℎ = 𝑃 + 𝜌𝑣 + 𝜌𝑔ℎ, 2, 2, 1, 𝑃 + 𝜌𝑣 + 𝜌𝑔ℎ = 𝑐𝑜𝑛𝑠𝑡𝑎𝑛𝑡, 2, That is,𝑝𝑟𝑒𝑠𝑠𝑢𝑟𝑒 𝑒𝑛𝑒𝑟𝑔𝑦 + 𝑘𝑖𝑛𝑒𝑡𝑖𝑐 𝑒𝑛𝑒𝑟𝑔𝑦 + 𝑝𝑜𝑡𝑒𝑛𝑡𝑖𝑎𝑙 𝑒𝑛𝑒𝑟𝑔𝑦 = 𝑐𝑜𝑛𝑠𝑡𝑎𝑛𝑡, The work done on a unit volume of fluid by the surrounding fluid is equal to the sum of, the changes in kinetic and potential energies per unit volume that occur during the flow. That is, State Institute of Technical Teachers’ Training & Research, , |, , Page, , 127

Page 140 :
Applied Physics - !, , total energy associated with flowing ideal fluid is a constant. Bernoulli’s theorem states that the, sum of kinetic energy, potential energy, and pressure energy of an ideal fluid in a streamline, flow remains constant throughout the flow., , 4.4.6 Applications of Bernoulli’s theorem, a) Atomizer, An atomizer is a device to spray a liquid or make a liquid into a jet of tiny droplets., like in, body spray, spray painting, car wash stations, etc. The principle behind the working of atomizers, is Bernoulli’s theorem. According to Bernoulli’s theorem, the velocity of a fluid increases in a, region, the pressure decreases in that region, and vice versa in order to maintain the total energy, as constant., , Fig. 4.8 Schematic diagram of an atomizer, The schematic diagram of an atomizer is shown in the figure. The essential parts of the, atomizer are a cylinder C with a piston P, a narrow T section pipe, and a container to fill the, liquid to be sprayed. As we push the piston rapidly to inside, the air in the cylinder begins to, move towards the T section pipe. Since the area of cross-section of the cylinder is larger than the, area of the cross-section of the T section pipe, as a consequence of the continuity equation the, velocity of air moving through the T section pipe is greater than the velocity of air in the, cylinder. According to Bernoulli’s theorem, the pressure in the T section pipe must be lower than, the pressure at the surface of the liquid in the container. Because of this pressure difference, the, State Institute of Technical Teachers’ Training & Research, , |, , Page, , 128

Page 141 :
Applied Physics - !, , liquid in the container rises up and reaches the T junction pipe. The liquid mixes with high-speed, air to form a spray. For a perfume bottle or spray paint, the container with liquid is kept at high, pressure with an air compressor. So, a small pressure difference created due to the press at the, spray piston will give a jet of liquid particle or atomized liquid., b) Airfoil, , Fig. 4.9 Cross sectional view of an air foil with streamlines of air, Airfoil is a special shape of solid objects which produces a lifting effect or floating effect, while moving in a streamlined fluid or air. The cross-section of wings of an airplane, boomerang,, wings of birds, propeller blade, turbine blade, etc. is some what with an airfoil shape. The, characteristic airfoil shape has a rounded leading edge followed by a sharp trailing edge and, curved surfaces as shown in Fig. 4.9. When the airfoil is moving against the streamlined air,, because of this special shape the streamlines might have a speed difference at the upper and, lower surfaces. If the air streams are moving at different speeds, so with different kinetic energy,, then according to Bernoulli’s theorem there will be pressure difference., Since the number of streamlines is more at the upper surfaces (remember the fluid layers, should not cross in streamline motion of fluids), the velocity of air is higher at the upper surface, of the airfoil (more streamlines at the same cross-sectional area cause increase in velocity)., Therefore, the kinetic energy of air at the upper side is higher. Then by Bernoulli’s theorem, the, pressure energy should be lesser at the upper side of the airfoil than on the lower side. That, State Institute of Technical Teachers’ Training & Research, , |, , Page, , 129

Page 142 :
Applied Physics - !, , means there is a lifting force from the lower side of the airfoil, which tries to float the airfoil, while it is in motion. This lifting effect comes into action only when the airfoil and streamlined, air are in relative motion. So, the lifting or floating motion of the paper plane or boomerang can, be understood with Bernoulli’s theorem. The airplane engine can use its energy to fly forward, and save energy for keeping the mass at the air floating because of the airfoil shape of wings., , Conceptual Learning 4.9, Can you relate the following everyday life experience to what we have learned here?, a) We may feel that we are pulled aside to a fast-running truck or bus just near to us. Or, when we are standing at the railway station platform and a train which does not have a, stop at that station passing just near to us with very high speed., b) The motion of a boomerang, c) The motion of a kite, , 4.5 VISCOSITY, The viscus force is analogous to the frictional force in mechanics. Consider a glass plate, placed at an inclination of 45 degrees. Let us pour a drop of water and honey at the elevated side, at two points with the same height. Observe, what happened. The water drops easily flow, downward while the honey does not. What it means, both are in the liquid state, but they are not, behaving alike. There are some internal forces to resist the motion of fluids. That force is called, viscus force., It is the property of a fluid by virtue of which it tends to resist the relative motion between, the layers of the fluid is called viscosity. We know that the fluid under streamline motion moves, as liquid layers that do not cross together. They move one above the other. So, there is relative, motion between the liquid layers., , State Institute of Technical Teachers’ Training & Research, , |, , Page, , 130

Page 143 :
Applied Physics - !, , 4.5.1 Coefficient of viscosity, , Fig. 4.10 Flow of liquid in layers over a solid surface, , Consider the flow of a liquid over a solid surface. Fig.4.10 shows a few representative, layers of the flowing liquid. The layer of the liquid in contact with the solid surface has zero, velocity and velocity of the layers of the liquid increases with the distance of the layers from the, solid surface. The viscous force (F) acting between two layers of the liquid is directly, proportional to the area of liquid layers and the velocity gradient between the layers (v 2 - v1 / d)., Combining these proportionalities, we can write,, 𝐴(𝑣2 − 𝑣1), 𝑑, 𝐴(𝑣2 − 𝑣2), 𝐹=𝜂, 𝑑, 𝐹𝛼, , The constant of proportionality η is called the coefficient of viscosity of the fluid. Therefore, the, co-efficient of viscosityη can be defined as that much resistive force developed between the, liquid layers of unit area when they are moving with a unit velocity gradient. The SI unit of, coefficient of viscosity η is kgm-1s-1 or Nsm-2., , 4.5.2Terminal velocity, Consider an object falling through a viscous medium. At first, the object will accelerate, due to gravity acting on the mass of the object while the viscus force or frictional analogue in, fluid dynamics and buoyant force opposes this motion of the object. Finally, an equilibrium may, State Institute of Technical Teachers’ Training & Research, , |, , Page, , 131

Page 144 :
Applied Physics - !, , occur between the downward gravitational force and opposing forces. Thus, the net force on the, body becomes zero and it stops accelerating and descent with a uniform velocity. This uniform, velocity is called terminal velocity., , Conceptual Learning 4.10, Why there are no humans get killed by hitting raindrops? [We know that the clouds occur at, roughly 3 km to18 km altitude, then a raindrop with a small mass may kill humans and other, organisms as it accelerates at a rate of 9.8 m/s 2], , 4.5.3Stokes’s law, When a body falls through a fluid, it drags the layer of the fluid in contact with it. As we, know the viscus force that is the relative motion between the different layers of the fluid is, equivalent to the frictional motion in Mechanics. The body under motion through the fluid, experiences a retarding force. It is observed that the viscous force is proportional to the velocity, of the object and is opposite to the direction of motion. The other quantities on which the force F, depends on viscosity η of the fluid and radius a of the sphere (consider the shape of body as a, sphere for simplicity in the calculation). Sir George G. Stokes (1819-1903), an English scientist, introduced an expression for the viscous drag force F as given below., 𝐹 = 6𝜋𝜂𝑟𝑣, Where η is the co-efficient of viscosity of the medium, r is the radius of the spherical, body and v is the uniform velocity after equilibrium or terminal velocity., , State Institute of Technical Teachers’ Training & Research, , |, , Page, , 132

Page 145 :
Applied Physics - !, , Conceptual Learning 4.11, Consider that we are going to drop a spherical object of radius 1 mm made of steel with, density 7.801 x 103 kg/m3into the following fluids as given in the table below. Use the, information given in the table and answer the following questions., 1. Find out the type of liquid with maximum terminal velocity?, 2. Arrange the liquids with their increasing order of terminal velocity?, 3. Find out the type of liquid with minimum terminal velocity?, , Name of Fluid, , Co-efficient of, , Density, , viscosity (μPas), , (103kg/m3), , Acetone, , 330, , 0.792, , Ethyl alcohol, , 1192, , 0.789, , Methyl alcohol, , 591, , 0.793, , Benzene, , 649, , 0.921, , Glycerol, , 141.2x104, , 1.26, , Nitric acid, , 1770, , 1.31, , Sulphuric acid, , 22x103, , 1.834, , turpentine, , 1490, , 0.86, , Kerosene, , 1460, , 0.82, , Toluene, , 585, , 0.867, , Heavy water, , 1260, , 1.1, , State Institute of Technical Teachers’ Training & Research, , |, , Page, , 133

Page 146 :
Applied Physics - !, , PRACTICE PROBLEMS, 1. A 200 kg load is hung on a wire of length 4.00 m, cross-sectional area 0.2 x 10 -4 m2, and, Young’s modulus 8.00 x 1010 N/m2. What is its increase in length? (Ans: 4.9 mm), 2. A steel wire of diameter,1 mm can support a tension of 0.5 kN. A steel cable to support a, tension of 25 kN should have a diameter of what order of magnitude?(Ans: 7.07 mm), 3. 250 L oil of compressibility k = 20 x 10-6 atm-1 is subjected to a hydraulic press. Find the, decrease in the volume of the oil when it is subjected to a pressure 1.6x10 7 Pa?(Ans: 0.82, m3), 4. How much load is needed to elongate a steel wire to 0.5% of its original length? The, diameter of the wire is 2 mm and Young’s modulus of the material of the wire is 20 x, 1010 N/m2.(Ans: 320.4 kg), 5. A wire of length 2 m is subjected to longitudinal stress by fixing the one end and hanging, 500 kg mass at the other end. If the wire stretched for a length of 5 mm and its Young’s, Modulus is 9.1 x 1010 N/m2, calculate the radius of the wire? (Ans: 2.62 mm), 6. Let a steady stream of water flow from a kitchen tap. At the tap, the diameter of the, stream is 0.85 cm. The stream fills a 150 cm3 container in 15 s. Find the diameter of the, stream 10.0 cm below the opening of the tap?, (Find the cross-sectional area of steady smooth flow of water with diameter 0.85 cm and, apply continuity equation in fluid dynamics to find the velocity of flow there. Equate the, product of the area of cross-section and velocity with volume flow rate. Then, treat this as, initial velocity and find the final velocity after a displacement of 10 cm with an, acceleration of 9.8 m/s2, since the motion is under gravity. Use equations of motion, under uniform acceleration. Now again apply the continuity equation to find the area of, cross-section and hence the diameter of steady smooth flow which is narrowed due to an, increase in velocity.Ans: 2.62 mm), 7. A copper rod of cross-sectional area 0.5 cm2 and length 1.00 m is elongated by 2 x 10-2, mm and a steel rod of the same cross-sectional area but 0.100 m in length is elongated by, 1.5 x 10-3 mm. Which rod undergoes greater tensile strain? (Ans: Copper), 8. Water is flowing in a pipe with a varying cross-sectional area. At point 1 the crosssectional area of the pipe is 0.075 m2 and the magnitude of the fluid velocity is 4 m/s (a), State Institute of Technical Teachers’ Training & Research, , |, , Page, , 134

Page 147 :
Applied Physics - !, , What are the fluid speed at points in the pipe where the cross-sectional area is 0.15 m 2 (a), and (b) 0.05 m2 (c) Calculate the volume of water discharged from the open end of the, pipe in 1.00 hour? (Ans: (a). 2 m/s, (b). 6 m/s and (c). 1080 m 3), 9. Water is flowing in a pipe with a circular cross-section but with varying cross-sectional, area (a) At one point in the pipe, the radius is 6 cm. What is the speed of the water at this, point if water is flowing into this pipe at a steady rate of 1.20 m 3/s? (b) At a second point, in the pipe, the water speed is 3.5 m/s. What is the radius of the pipe at this point? (Ans:, (a). 106.16 m/s, (b). 0.33 m), 10. A shower head has 25 circular openings, each with a radius of 1.5 mm. The shower head, is connected to a pipe with a radius of 1.0 cm. If the speed of water in the pipe is 5 m/s,, what is its speed as it exits the showerhead openings? (Ans: 5.32 m/s), QUESTIONS, 1. Define stress and strain? And comment on their unit?, 2. Explain Hooke’s Law, 3. Explain Moduli of elasticity and give their expressions?, 4. Explain why there is no value for Young’s modulus and rigidity modulus for liquids and, only Bulk modulus?, 5. Explain the tensile strength of a material?, 6. Define hydrostatic pressure and explain Pascal’s law?, 7. Define the pressure one Pascal?, 8. Why pressure is not a vector quantity?, 9. Why do mountaineers get bleed through their nose or ear at high altitudes?, 10. Describe the terms gauge pressure and absolute pressure?, 11. Mention the types of attraction between molecules?, 12. Describe the hydrophilic and phobic surfaces considering the angle of contact?, 13. Write a short note on the ascent formula?, 14. Distinguish between streamline and turbulent flow of fluids?, 15. What is Reynold’s number? Mention its importance?, 16. Explain continuity equation in fluid dynamics and how it is related to the law of, conservation of mass?, State Institute of Technical Teachers’ Training & Research, , |, , Page, , 135

Page 148 :
Applied Physics - !, , 17. Give an account of different types of energies associated with the flow of fluids?, 18. Explain Bernoulli’s theorem?, 19. Describe the working of an atomizer with a neat diagram?, 20. Explain why there is a floating effect while the airfoil and fluid are in relative motion?, 21. Define the coefficient of viscosity of a liquid and mention its unit?, 22. What is meant by the terminal velocity of a body?, 23. Explain Stokes’s law?, , State Institute of Technical Teachers’ Training & Research, , |, , Page, , 136

Page 149 :
Applied Physics - !, , Bibliography, 1., , Text Book of Physics for Class XI& XII (Part-I, Part-II); N.C.E.R.T., Delhi, , 2., , Applied Physics, Vol. I and Vol. II, TTTI Publications, Tata McGraw Hill, Delhi, , 3., , Concepts of Physics by HC Verma, Vol. I & II, Bharti Bhawan Ltd. New Delhi, , 4., , Fundamentals of Physics, Halliday/Resnick/Walker, Wiley India Pvt. Ltd, , 5., , Modern approach to Applied Physics-I and II, AS Vasudeva, Modern Publishers., , State Institute of Technical Teachers’ Training & Research, , |, , Page, , 137

Page 150 :
Applied Physics - !, , Revised Syllabus (Revision 2021), Program: Diploma in Engineering, Course Code:, , Course Title: Applied Physics-I, , Semester: 1, , Credits: 3, , Course Category: Basic Science, Periods/Week: 3 (L:2 T:1 P:0), , Periods/Semester: 45, , Course Objectives:, ,  To provide students with a broad understanding of physical principles of the, universe to help them develop critical thinking and quantitative reasoning, skills, ,  To help the diploma engineers in applying the basic concepts of physics to, solve broad-based engineering problems, Course Pre-requisites:, , Course code, , Topic, , Semester, , Course name, Secondary Level, Physics, , Basic knowledge in Physics, , Course Outcomes, On completion of the course student will be able to:, , Duration Cognitive, Level, (Hours), , CO No., , Description, , CO1, , Apply laws of mechanics in rocket propulsion and, recoil of gun., , State Institute of Technical Teachers’ Training & Research, , |, , 9, , Applying, , Page, , 138

Page 151 :
Applied Physics - !, , CO2, , Apply concepts of circular motion and rotational, motion, , 10, , Applying, , CO3, , Make use the concepts of energy, power, work,, temperature and friction to solve problems, , 13, , Applying, , CO 4, , Use the theorems of fluid dynamics in atomiser and, airfoil, , 13, , Applying, , CO-PO Mapping with values, Course Outcomes, , PO1, , CO1, , 3, , CO2, , 3, , CO3, , 3, , CO4, , 3, , PO2, , PO3, , PO4, , PO5, , PO6, , PO7, , Course Outline, Duration, (Hours), , Description, , Cognitive Level, , CO 1: Apply laws of mechanics in rocket propulsion and recoil of gun., M1.01, , Discuss various physical quantities and their units., , 1, , Understanding, , M1.02, , Identify types of errors in measurements and apply, it to calculate errors in laboratory experiments., , 2, , Applying, , M1.03, , Differentiate a physical quantity into scalar and, vector and discuss various methods of vector, addition., , 2, , Understanding, , M1.04, , Apply Newton’s laws of motion and law of, conservation of linear momentum to describe, rocket propulsion and recoil of gun., , 4, , Applying, , State Institute of Technical Teachers’ Training & Research, , |, , Page, , 139

Page 152 :
Applied Physics - !, , Module 1: Measurements and Force, Physical quantities - Fundamental and derived, Units and systems of units (CGS, MKS, and SI units),, Measurements: Errors in measurements- systematic and random errors (qualitative idea, only), absolute error, relative error, percentage error, numerical problems, Scalar and Vector quantities – representation of vector, Collinear vectors, Coplanar, vectors, equal vectors, unit vectors. Addition and Subtraction of Vectors, Triangle and, Parallelogram law of addition, Resolution of a Vector., Equations of motion (elementary idea), Newton’s laws of motion (no derivation), Force,, Momentum, Statement and derivation of conservation of linear momentum, its applications recoil of gun and rockets, Impulse and its examples (numerical problems related to force and, momentum)., CO 2: Apply concepts of circular motion and rotational motion, , M2.01, , Describe basic concepts of circular motion, and its application in the case of banking, of roads and railway tracks., , 4, , Applying, , M2.02, , Explain rotational motion and theorems of, moment of inertia., , 3, , Understanding, , M2.03, , Discuss the conservation of angular, momentum and torque in rotational, motion., , 2, , Understanding, , 1, , Series Test – I(Module 1 &2), , Module2: Rotational Motion, Circular motion, angular displacement, angular velocity, angular acceleration, Relation, between linear and angular velocity, linear acceleration and angular acceleration. Centripetal, State Institute of Technical Teachers’ Training & Research, , |, , Page, , 140

Page 153 :
Applied Physics - !, , acceleration and Centripetal force (qualitative idea only). Application - banking of roadsand, railway tracks (numerical problems related to circular motion), Moment of inertia and its physical significance, radius of gyration for rigid body,, Theorems of parallel and perpendicular axes, Moment of inertia of rod, disc, ring and sphere, (hollow and solid)- (Formulae only), Definition of angular momentum and torque, Conservation of angular momentum, (quantitative)., CO 3: Make use the concepts of energy, power, work, temperature and friction to, solve problems, M3.01, , Explain the concept of work and friction., , 3, , Understanding, , M3.02, , Describe conservation of energy and, transformation of energy into various forms, , 2, , Understanding, , M3.03, , Discuss the concept of power and apply it to, solve engineering problems., , 4, , Applying, , M3.04, , Discuss the concepts of heat and, measurement of temperature using mercury, thermometer and pyrometer, , 4, , Applying, , Module 3: Work, Energy, Power and Heat, Definition of work and unit, Work done in moving an object on horizontal plane,, Friction: definition, static friction, kinetic friction, laws of friction, methods of reducing, friction and examples., Energy and its units, kinetic energy, potential energy with examples. conservation of, energy for freely falling bodies, Various forms of energy, transformation of energy (mention, examples), Power- definition, power and work relationship, calculation of power (numerical, problems related to energy and power)., Concept of heat and temperature, scales of temperature and their relationship (numerical, problems relating various temperature scales), modes of heat transfer (conduction, convection, State Institute of Technical Teachers’ Training & Research, , |, , Page, , 141

Page 154 :
Applied Physics - !, , and radiation with examples), specific heat of solids, measurement of temperature - Mercury, thermometer and Pyrometer., , CO 4: Use the theorems of fluid dynamics in atomiser and airfoil, Explain the basic concepts of elasticity and, apply it to calculate various elastic modulii of, materials, , 4, , Applying, , Discuss properties of fluids such as surface, tension and pressure., , 2, , Understanding, , M4.03, , Define the term coefficient of viscosity and, explain Stoke’s law, , 2, , Understanding, , M4.04, , Apply theorems of fluid dynamics to explain, the working of atomiser and air foil, , 4, , Applying, , M4.01, , M4.02, , Series Test – II (Module 3 &4), , 1, , Module 4: Properties of Matter, Elasticity: definition of stress and strain, Hooke’s law, modulii of elasticity (numerical, problems)., Pressure: definition and units, atmospheric pressure, gauge pressure and absolute, pressure., Surface tension: concept, units, cohesive and adhesive forces, angle of contact, Ascent, Formula (No derivation), mention two applications of surface tension, effect of temperature, and impurity on surface tension., Viscosity and coefficient of viscosity: Terminal velocity, Stoke’s law. Hydrodynamics:, Fluid motion, stream line and turbulent flow, Reynold’s number (qualitative idea only),, Equation of continuity (numerical problems of equation of continuity), Bernoulli’s Theorem, and its applications (air foil, atomizer)., , State Institute of Technical Teachers’ Training & Research, , |, , Page, , 142

Page 155 :
Applied Physics - !, , MODEL QUESTION PAPER, , APPLIED PHYSICS -I, Time:3 Hour, , Max. Marks: 75, PART A, , I., , Answer all the following questions in one word or one sentence, 1., , Mole is the unit for ---------, , 2., , Pick out the scalar quantities from the following, a) velocity b) displacement c) work d) force, , 3., , The analogous physical quantity of displacement in circular motion is----------., , 4., , Moment of inertia of a sphere about its diameter is --------------., , 5., , Write the SI unit of power., , 6., , The mode of heat transfer by the movement of particles is -------------., , 7., , Define stress., , 8., , Capillary rise is connected with the phenomenon of --------., , 9., , Suggest a lubricant that can be used for light machines like watches., (9 x 1 = 9 marks), PART B, , II., , Answer any eight questions from the following. Each question carries 3 marks., 1., , Correct the following statements., a) The rate of change of speed is known as acceleration, b) A freely falling stone is moving with constant speed., c) Two vectors each of magnitude P acting in the opposite direction have the, resultant 2P., , 2., , Derive the relation between torque and angular momentum., , 3., , Explain the working of a pyrometer with a schematic diagram., , State Institute of Technical Teachers’ Training & Research, , |, , Page, , 143

Page 156 :
Applied Physics - !, , 4., , Convert 300 K into Celsius scale and Fahrenheit scale., , 5., , Give three practical applications of conduction of heat., , 6., , Write a brief note on solar energy., , 7., , Which boils faster; milk or water? Comment your answer, , 8., , Write a note on gauge pressure., , 9., , Young’s moduli of certain materials are given in the table. Make a comparative, study of the materials when stretched by the same load., , 10., , Material, , Yx1010 N/m2, , Steel, , 20.0, , Glass, , 5.5, , Rubber, , 0.05, , Copper, , 11.0, , Distinguish between elasticity and plasticity with examples., (8 x 3 = 24marks), , PART C, Answer all questions. Each question carries 7 marks, III., , A car moving with a momentum P. If the velocity of the car changes at a certain instant, and its momentum increases by 100%. Calculate the increase in kinetic energy of the, car., OR, , IV., , In measurement with a scale, the length of a table is observed as 2.18 m, 2.22 m, 2.19, m, and 2.20 m. Find the percentage error in measurement., , V., , Discuss the conservation of angular momentum with an example., OR, , VI., , Calculate the angle of banking for a circular track of radius of curvature 200 m suitable, for a maximum speed of 40 m/s., , State Institute of Technical Teachers’ Training & Research, , |, , Page, , 144

Page 157 :
Applied Physics - !, , VII. How can we add two vectors in the following situations?, a) Two vectors in the same direction., b) Two vectors in the opposite direction., c) If the two vectors are not parallel to each other., OR, VIII. The particle executes 400 revolutions in a minute along a circle of radius 20 cm., Calculate linear velocity and angular velocity., IX., , A crane that lifts a load produces a tension of 4500 N in the cable attached to the load., If the motor winds the cable at the rate of 2 m/s. Estimate the power of the engine of, the crane., OR, , X., , Explain different modes of heat transfer., , XI., , Friction is a necessary evil. Give a proper explanation of the statement. State laws of, friction., OR, , XII. A metal wire of length 10 m and diameter 1 mm is stretched by hanging a mass of 14, kg at one end and keeping the other end fixed to a sealing. Find the extension produced, if the Young’s Modulus of the material of the wire is Y = 7 x 10 10 N/m2., XIII. a) Explain the elementary idea of surface tension., b) If the clothes have grease stains on them, washing with water will not remove these stains., Suggest a solution to the problem and explain it., , OR, XIV. State Bernoulli’s theorem. Explain an application of Bernoulli’s theorem., , 6 x 7 = 42 Marks, , State Institute of Technical Teachers’ Training & Research, , |, , Page, , 145