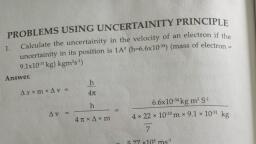Page 1 :
Quantum Numbers, The set of numbers used to describe the position and energy of the electron in an, atom are called quantum numbers. There are four quantum numbers, namely,, principal, azimuthal, magnetic and spin quantum numbers., Principal Quantum Number, , , Principal quantum numbers are denoted by the symbol ‘n’. They, designate the main shell of the electron in the atom. A larger value of the, principal quantum number implies a greater distance between the electron, and the nucleus. It gives an idea about energy and size of the shell., Maximum number of the electrons present in the shell is 2n 2., , , , It is represented by the letter n. n can have values 1, 2, 3, ….. That is any, integer other than zero., , , , The value n = 1 denotes the innermost electron shell of an atom, which, corresponds to the lowest energy state (or the ground state) of an electron., , Azimuthal Quantum Number (Orbital Angular Momentum Quantum, Number), , , The azimuthal (or orbital angular momentum) quantum number describes, the shape of a given orbital. It is denoted by the symbol ‘l’. It gives an idea, about the number of sub-shells present in any main shell, relative energies, of subshell, and shapes of orbital present in any sub-shell., , , , The value of the azimuthal quantum number can indicate either an s, p, d,, or f subshell which vary in shapes. This value depends on the value of the, principal quantum number, i.e. the value of the azimuthal quantum number, ranges from 0 to (n-1).

Page 2 :
, , For example, if n = 3, the azimuthal quantum number can take on the, following values – 0, 1, and 2. When, l =0, ‘s’ subshell., l =1, ‘p’ subshell., l =2, ‘d’ subshell., l =3, ‘f’ subshell., , , , , Therefore, when n = 3, the three possible subshells are 3s, 3p, and 3d., In another example where the value of n is 5, the possible values of l are 0,, 1, 2, 3, and 4., , Magnetic Quantum Number, The total number of orbitals in a subshell and the orientation of these orbitals are, determined by the magnetic quantum number. It is denoted by the symbol ‘m’., The value of the magnetic quantum number depend on the value of the azimuthal, (or orbital angular momentum) quantum number. For a given value of l, the value, of m ranges between the interval -l to +l. Therefore, it indirectly depends on the, value of n., For example, if n = 4 and l = 3 in an atom, the possible values of the magnetic, quantum number are -3, -2, -1, 0, +1, +2, and +3., Azimuthal, , Quantum, , Corresponding Number of, , Number Value, , Orbitals (2l + 1), , 0 (‘s’ subshell), , 2*0 + 1 = 1, , Possible Values of ml, , 0

Page 3 :
1 (‘p’ subshell), , 2*1 + 1 = 3, , -1, 0, and 1, , 2 (‘d’ subshell), , 2*2 + 1 = 5, , -2, -1, 0, 1, and 2, , 3 (‘f’ subshell), , 2*3 + 1 = 7, , -3, -2, -1, 0, 1, 2, and 3, , The total number of orbitals in a given subshell is a function of the ‘l’ value of, that orbital. It is given by the formula (2l + 1). For example, the ‘3d’ subshell (n=, 3, l=2) contains 5 orbitals (2*2 + 1). Each orbital can accommodate 2 electrons., Therefore, the 3d subshell can hold a total of 10 electrons., Electron Spin Quantum Number, , , The value of this number gives insight into the direction in which the, electron is spinning, and is denoted by the symbol s., , , , The value of s offers insight into the direction in which the electron is, spinning. The possible values of the electron spin quantum number are +½, and -½., , , , The positive value of s implies an upward spin on the electron which is, also called ‘spin up’ and is denoted by the symbol ↑. If s has a negative, value, the electron in question is said to have a downward spin, or a ‘spin, down’, which is given by the symbol ↓.