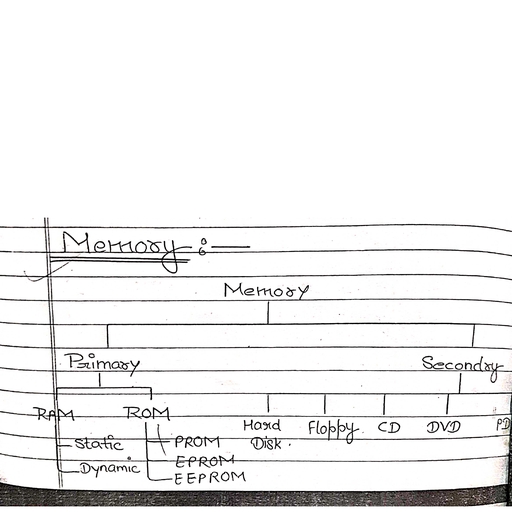
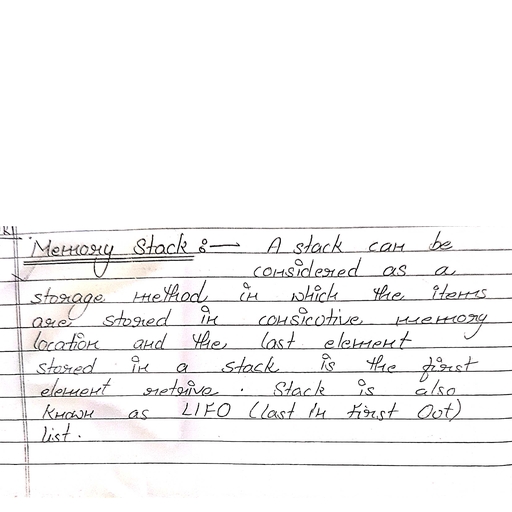
Page 1 :
as Three Hours ] 5 [, , Maximum Marks : 79, Answer five QUestion. ip, , (ii) Question No. 1 is ompulsory,, , Note: (i), , (iii) Answer = remaining fou, questions,, , selecting two from each Section A and B., (iv) All questions carry equal marks., , (v) Symbols have their usual meaning., , 1. Answer all part of the following :, , ‘ i i an, (a) Define universal and void relation with, , example.

Page 2 :
££ lll, , 1476/1, (b) Let f:R (2), >A be given by, , f(x) = x2 -2, , \, find (0, > = (uw, )'-2, Sx, = Ie, , (c) If Ais a symmetric matrix,, , N= ©, us, , = Oo x, , then find x, y, 2., , cast the following cumulative table in, , , , , , (d) Re, the form of an ordinary frequency, distribution :, , No. of DayS Absent | No. of Students, Less than 5 29, Less than 10 224, Less than 16 465, , , , , n2, Less tha 0 582

Page 3 :
(3) | 4476/|, , , , , , , , Less than 25 634, , Less than 39 644, , Less than 35 650, , Less than 40 653, , Less than 45 655, SECTION -~A, , 2. (a) Give the power sets of the following : |, (i) {a, {b}}, , (ii) (1, }, , , , , , , (b) Show that:, , AcAUBandAnBcA, , Bi (a) If A\= (1, 3, 5), B= (2, 4, 6}, C= (2, 4, 5), Galculate’A x B, Bx Aand Ax(BUC),, , P.T.0,

Page 4 :
(4), , 476/| ;, : ofine equivalence relation. Also, show that, if, , (b), S = (1,2. 3) and R= (1,1) (1 2) (1s 2), (2, 1,, , then R is not an equivalence folation., 4; (a) The first term of a series Is 5, the last 45 ang, the sum 400. Find the number of terms ang, , the common difference., , (b) Find the three number in G.P. whose sum is, 19 and whose product is 216., , 5. (a) If @ is one of the imaginary cube roots of, unity, find the value of :, , 1 o, o wo |, wo 1 o, (b) If:, ke, a-| al 5-| 5 0, ter 3 -§ -6 7, S, L tren show that. (AB) x aT BT, es Sree.

Page 5 :
Wand Pray, ew, SECTION -B, , 6. (a) .List al Possible functions from X =, =.{0,, , (b) Let X= {1, 2, 3} and ¢ g, h and s be functions, from X to X given by, , f= {<1, 2>, <2, 3>, <3, 1), g={<1, 2>, <2, 1>, <3, 3>}, h={<1, 1>, <2,.23) <3, 1>}, S= {<1, 1>, <2; 25; <3, 3>}, , Find fog, gof, fohog, sos and fos., , i Iso, 7. (a) Expand, (x—3)'5 by binomial theorem. Als, find it's 10th term,