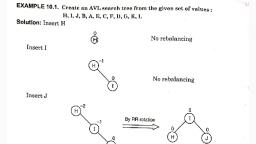
Page 1 :
The first balanced binary search tree was the AVL, tree (named after its discoveries, Adelson Velskii, and Landis). The AVL tree is a binary search tree, that has an additional balance condition. This, palance condition must be easy to maintain and, ensures that the depth of the tree is O (log NV). The, simplest idea is to require that the left and right, sub-trees have the same height. Recursion dictates, that this idea applies to all nodes in the tree, since, each node is itself a root of some sub-tree. This, - balance condition ensures that the depth of the tree, is logarithmic, but it is too restrictive because it is, too difficult to insert new items while maintaining, balance. Thus the AVL trees uses a notion of, balance that is somewhat weaker but still strong, , enough to guarantee logarithmic depth., , , , Fig. 10.1. Two binary search trees : the left tree is AVL, tree, but the right tree is not (unbalanced nodes are, ' | darkened), , Scanned with CamScanner
Page 2 :
AVL is a height balanced tree. A height balanced tree is one in which the difference in the, height of the two sub-trees for any node is less than or equal to some specified amount. In AVL, tree, the height difference may be no more than 1. In fact for an AVL tree it will never be greater, than 1.44 log (n + 2). Because of this, the AVL tree provides a method to ensure that tree, searches always stay close to the theoretical minimum of 0 (log n) and never degenerate to O(n)., , Definition, - An empty binary tree B is an AVL tree., * IfBis the non-empty binary tree with B, and B, are its left and right sub-trees then Bis, an AVL tree if and only if:, (a) B, and Bp are AVL trees, and, , (b) |hy—hgl <1, where hy and hp are the heights of B, and Bp sub-tress, respectively., , Scanned with CamScanner
Page 3 :
H 10.2 BALANCE FACTOR, To implement an AVL tree each node must contain a balance factor, which indicates its state., of balance relative to its sub-trees., If balance is defined by, Height of left sub-tree — Height of right sub-tree, an have values of -1, 0 or 1. In figure, numbers, , then the balance factors in a balanced tree ¢, placed near the nodes indicate balance factors., , , , (b), , , , Fig. 10.2., , For an AVL tree, the value of the balance factor of any node is —1, 0, or 1. If it is other than, these three values then the tree is not balanced or it is not an AVL tree. If the value of the, balance factor of any node is 1, then the height of the right sub-tree of that node is one mor?, than the height of its left sub-tree. If the value of the balance factor of any node is 0 then the, height of its left and right sub-tree is exactly the same. If the value of the balance factor of any, node is 1 then the height of the left subtree of that node is one more than the height of its nie, , , , sub-tree., height: -balanced binary tree is alee a binary search tree anda complete b bina, ee is slwaye height balanced, but the reverse is not true. i :, , , , , , Scanned with CamScanner
Page 4 :
a PRESENTATION OF AN AVL TREE, , j 10.3 RE, , AVL search sented using a linked representation., , to represent a node of an AVL tree four, ght child and an, , trees like binary search trees are repre, , wever, every node consists of its balance factor. So, i, pe are required-one for data, two for storing the address of the left and ri, , 4 additional field is required to hold the balance factor., , , , , , , , Left Info BF Right, , , , , , , , , , Node, , Figure shows the representation of an AVL tree., . +1, , , , Fig. 10.3., , The number against each node represents its Balance Factor (BF). The linked representation, , of above tree is as follows :, , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , 225| 20 | +1 | 240, 210, 225 7 —, 236| 10 | +1 aT] 274| 30 | O | 280 240, 300] 8 | +1] Null Null} 15} 0 | Null Null} 26 | O | Null Null} 40 | O | Null, [ 236 250 274 280, [a] 5 | o [Null, 300, Fig. 10.4., , Scanned with CamScanner