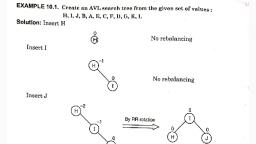
Page 1 :
A binary search tree is a binary tree. Such a, tree can be represented by a linked data structure, in which each node is an object. In addition to a, key field, each node contains fields left, right and, p, that point to the nodes corresponding to its left, child, its right child and its parent respectively. The, keys in a binary search tree are always stored in, such a way as to satisfy the binary-search tree, , properties., , , , i 9.2 BINARY-SEARCH TREE PROPERTIES, , Abinary search tree may be empty. If it is not empty, then it satisfies the following properties :, , (1) Every element has a key, i.e., key (x) for, element x and no two elements have the, same key., , (2) The keys (if any) in the left sub-tree are, smaller than the key in the root., , (3) The keys (if any) in the right sub-tree are, larger than the key in the root., , (4) The left and right sub-trees are also binary, search trees., , Let x be a node in a binary search tree., , , , Scanned with CamScanner
Page 2 :
+ ify is a node in the left sub-tree of x, then, , key [y] < key [x], + ify is a node in the right sub-tree of x, then, , key [x] < key [y], , , , , , , , , , , , , , , , A binary search tree, , Fig. 9.1., , In this tree key [x] = 60, if y is the node in the left sub tree then key [y] = 25, , Le., key [y] < key [x], and if y is the node in the right sub tree then key [y] = 70, ie., key [y] 2 key [x], , 4P, T, Parent, Key, Left Right, £. ae, x, , Node structure, , Scanned with CamScanner
Page 3 :
f 9.3 VARIOUS OPERATIONS ON A BINARY SEARCH TREE, , The most common operation performed on a BST is searching for a key stored in the tree., Besides the search operation. Binary search trees can support many operations such as minimum, , key. Maximum key, successor and predecessor. These operations run in O(h) time, where h is, the height of the tree., , (a) Searching in a BST, , Searching for a data in a binary search tree is much faster than in arrays or linked lists., The TREE-SEARCH (x, k) algorithm searches the tree root at x for a node whose key value, equals to k. It returns a pointers to the node if it exists otherwise NIL., , TREE-SEARCH (x, k), 1. Ifx = NIL or k = key [x], , 2 then return x, 3. Ifk < key [x], 4, , then return TREE-SEARCH (left [x], k), 5. else return TREE-SEARCH (right [x], k)., , Note : Search operation takes time O(h), where h is the height of a BST., , Scanned with CamScanner
Page 4 :
sample :, , Fig. 9.2., Suppose TREE-SEARCH (x, 14), Here x # NIL and key [x] = 16 which is not equal to k., Here k = 14 and 14 < 16 (True), then TREE-SEARCH (left (x), k), ic., now left [x] becomes x. (12 node), , Fig. 9.3., Now x#NILand 14 #12, 14«12, So, TREE-SEARCH (right [x], 14), , Le.,, , Fly. 0.4., Now x # NIL and k = key [x], So return x., , Scanned with CamScanner
Page 5 :
(6) Minimum and Maximum Key Element in BST . . ., The minimum key value element can always be found by following left child pointers from, , the root until a NIL is encountered., Tree-Minimum (x), 1. While left [x] NIL, 2. doxe¢ left [x], , 3. return x . . . ., and the maximum key value element can always be found by following right child pointers, , from the root until NIL is encountered., Tree-Maximum (x), 1. While Right [x] + NIL, 2. dox« Right [x], 3. return x, , (c) Successor of a Node x oo, The following procedure returns the successor of a node x in a BST if it exists and NIL if x, , has the largest key in the tree., , TREE-SUCCESSOR (x), . If right [x] + NIL, then return TREE-MINIMUM (right [x]), , - ¥ — pix], while y # NIL and x = Right [y], doxey, y< ply], return y, Example:, , On, oOny pe, , _, , , , Fig. 9.5., Suppose we want to find successor of node 55 then, we call TREE-SUCCESSOR (55), Here right [x] « NIL, So call TREE-MINIMUM (right [x]), i.e., TREE-MINIMUM (60), Here left (x) # NIL, So left (x) is now x, Le., xX & left (x), and return x, i.e., node 58., , Scanned with CamScanner