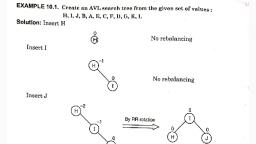
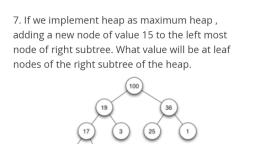
Page 1 :
1 8.6 STRICTLY BINARY TREE, , If every non-leaf node in a binary tree has non-empty left and right sub-trees, the tree is, termed as strictly binary tree, e.g.,, , , , , , Fig. 8.16 Strictly binary tree, , A strictly binary tree with n leaves always contains 2n—1 node., , Scanned with CamScanner

Page 2 :
I 8.7 COMPLETE BINARY TREE, , As we know, the depth of a binary tree is the maximum level of any leaf in the tree, This, equals the length of the longest path from the root to any leaf., , A complete binary tree of depth d is the strictly binary tree all of whose leaves are at, level d. ;, , ------------------------- > Level 0, Level 1, , Level 2, ~, , , , > Level 3, , Fig. 8.17. Complete binary tree of depth 3., , te, , Scanned with CamScanner

Page 3 :
If a binary tree contains m nodes at level I, it contain at most 2m nodes at level I +1,, Since a binary tree can contain atmost one node (root) at level 0, it can contain atmost 2!, , nodes at level I., A complete binary tree of depth d is the binary tree of depth d that contains exactly 21, , nodes at each level I between 0 and d., Thus, the total number of nodes in a complete binary tree of depth d equals the sum of, , the number of nodes at each level between 0 and d i.e.,, , Number of nodes at level 0 is 2°= 1, Number of nodes at level 1 is 2! = 2, Number of nodes at level 2 is 2?., , Number of nodes at level d is 24., The total number of nodes in complete binary tree is, , 294214924. o¢= 2,, 4, , By induction, it can be shown that this sum equals 2¢+1~ 1, Since all leaves in such 8, tree are at level d, the tree contains 2¢ leaves and therefore 2¢ — 1 non-leaf nodes., The significance of a complete binary tree is that it is the binary tree with the maximum, , number of nodes for a given depth., , Scanned with CamScanner

Page 4 :
— 8.8 ALMOST COMPLETE BINARY TREE, , A binary tree of depth d is an almost complete binary tree, if, , Scanned with CamScanner

Page 5 :
node at level less than d—1 has two childrens,, Any, , . de ‘x’ in the tree with a right descendant, 9. sas ay left descendant of x is either a leaf at leve, and é, , at level d, x must have a left child, 1d or has two childrens,, , , , (c), Fig. 8.18. ee, Fig, 8.18(a) is not almost complete binary tree because it contains leaf nodes at level 1,, and, , 3. So violating condition 1., , — evel 3. vever,, ig. 8.18(b) satisfies condition 1, since every leaf is either at ie a a ona, “ndition 2 is violated, since A has a right descendant at level 3 (, , *scendant that is a leaf at level 2 (E)., , Scanned with CamScanner