Page 1 :
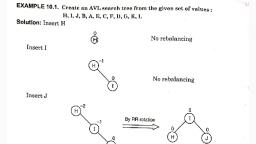
f 10.6 DELETION IN AN AVL TREE, The deletion of a node from an AVL tree is exactly the same as the deletion of a node from the, BST. The sequence of steps to be followed in deleting a node from an AVL tree is as follows :, , Initially, the AVL tree is searched to find the node to be deleted., , 1., The procedure used to delete a node in an AVL tree is the same as deleting the node in, , 2., the binary search tree., , 3. After deletion of the node, check the balance factor of each node., , Scanned with CamScanner

Page 2 :
4, Rebalance the AVL tree if the tree is unbalanced. For this, AVL rotati, , On deletion of a node x from the AVL tree. Let A be t Seahorses aes, yom X to the root node, with a balance factor of +2 or, is classified as Lor R depending on whether the deletion, of A. ., , Now depending on the value of balance factor of B, where B is the root of the left or right, gub-tree of A, the R or L rotation is further classified as RO, Rl and R—1 or LO, L1 and L-1., , RO Rotation and LO Rotation : When balance factor of B is 0, RO rotation is used., , +1 +2, , he closest ancestor node on the path, —2. To restore balance, the rotation occurred on the left or right sub-tree, , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , 0 0, (B) { Delete x (3) t, ' ‘ h ' h-1, h , x | h t \, ve B AR + An, L R B Ba, Unbalanced AVL tree, after deletion of x, Fig. 10.26. =, From RO rotation, we get - :, -1, B, +1, { A, “h, | ' {, h :!, BL t, Fig. 10.27., Example : Delete 90 from the AVL search tree shown in Fig. 10.27., +1, , , , Fig. 10.28. . :, After deletion of 90, we get unbalanced AVL tree, as, , Scanned with CamScanner

Page 3 :
RO Rotation, , , , Balanced AVL tree after Ro fotation, Fig. 10.29., , Similarly LO rotation is executed, when balance factor of B is zero and B is pe root of right, , sub-tree of A. LO rotation is executed as illustrated in Fig. 10.30., -2, , Delete 40, oe, , , , LO rotation, , , , Balanced AVL tree, Fig. 10.30., , R1 and L1 Rotation, If balanced factor of B is 1. R1 or L1 rotation is | R1 rotation as illustrated in aoe, below., , +1 +2, , (A) Delete A, , , , , , , , , , , , , , , , , , , , , , , , + s-— >, >, 4, , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , iL) Qe i Lh, By Ba B BL Ba AR Ba An, Unbalanced AVL tree Balanced AVL. tre, Fig. 10.31, :, , Scanned with CamScanner

Page 4 :
A, +1 L1 Rotation, t, B, 1, 4, , t h-1 hI :, , t y + }, , Fig. 10.32., , Example :, +2, Delete 60, , Balanced AVL Tree, Fig. 10.33., , RC1) and L(-1) Rotation, , ‘ Ifbalance factor of B is -1, then RCI) and L-1) rotation is used, R(-1) rotation is shown in, igure,, , Scanned with CamScanner

Page 5 :
Example:, , , , , , , , , , , , , , , , h Delete x, OF, , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , .B C. Cr An, Balance AVL Search Tree, Fig. 10.34,, , Delete 90, —, , Balance AVL Search Tree, Fig. 10.36., , Scanned with CamScanner