Page 1 :
8 8.14 HUFFMAN TREE, , As we have seen earlier that an extended Binary tree is a binary tree in which ever, has zero or two children. The nodes which have two children are called internal nog, which have no children are called external nodes., , In any 2 Tree the number of external nodes is 1 more than the number of interna] Nodes, , y Node, eS ang, , le,, , E=I+1, Wher E is the number of external nodes and J is the number of internal nodes,, , , , , , , , , , , , , , , , , , , , , , Fig. 8.55., , Internal nodes = 4, External nodes = 5, , We know, the path length for any node is the number of minimum nodes traversed, from root to that node. With this in mind, we define the External path length. Ly of a2 Tree, to be the sum of all path lengths i.e.,, , Lp= 2+34+8+2+9=12, Similarly total path length for internal nodes are, , L,;= 0+1+2+1=4, We can also get the total path length of external node through, , , , , , , , , , Lp= L,+2n, Where n is the total number of nodes in the tree., Here, Ly=4+2*4, = 4+8=12, , Suppose every external node has same weight W, then the weighted path length for the, external node will be, , P= WiL, + WyLy + Waly +0... + WL, , nn, , Where W; and L; denote respectively, the weight and path length of an external note., , nal, , Scanned with CamScanner

Page 2 :
reate different tre j, guppose we c ' ees which have same weigths on external nodes pl, + necessary that they have same weighted path length ernal nodes then it is, 7 th., , Let us take the weights 2, 7, 9, 10 and create three different trees, , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , 7 10, (a) (b), Fig. 8.56., , , , P=2*247*24+9*2+10*2=44+14+18+20=56, P,=2*14+7*34+10*3+9*2=24+21+30+18=71, P,=10*14+7*34+8*3+9*2=104+21+24+18=73, , We can see that three different trees have different path lengths even same tree of (0), and (c) have different path lengths. So the problem arises for obtaining a unique tree which, has minimum path length., , The general problem that we want to solve is as follows. Suppose a list of n weights is, given:, , Wy, Way os Wy, , Among all the 2-trees with n external nodes and with the given n weights, find a tree fT, , with a minimum weighted path length. Huffman gave an algorithm to find such a tree., , , , Huffman Algorithm:, , 1. Suppose, there are n weights Wy, Wo, ve W,.- ;, 2. Take two minimum weights among the n given weights. Suppose W, and Wy are first, , two minimum weights then sub-tree will be:, , , , Wy + W2, , , , , , , , , , Wy W, , , , , , , , , , , , 3. Now the remaining weights will be W, + Wy, Way Way ee Wis, ‘4. Create all sub-tree at the last weight. _ _ ee, , Thus, Huffman algorithm constructing the tree from the bottam up racher than trom, © top down approach., , Scanned with CamScanner

Page 3 :
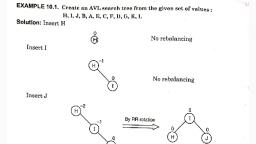
EXAMPLE 8.11. Suppose A, B, C, D, E, F and G are 7 elements with weights as follows., B Cc D E F | aqua, , , , Item A, , , , Weights | 15 10 5 3 7 12, , Create an extended binary tree by Huffman algorithm., Solution: Step 1: Taking two nodes with minimum weights fe., 3 and 5., , 6, ov, , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , Fig. 8.57., , Now elements in the list are:, 15 10 8 @ 12, , ir, a, , , , , , , , , , , , , , , , , , , , , , Step 2: Taking two minimum weight nodes which are § and 7 i.e., now., zr] (8), 3 5, Fig. 8.58., Now elements in the list are:, 25, , 15 10 15 12,, , Les; 15 10 (15) 12 25, , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , Fig. 8.59,, , Step 3: Taking two minimum weighted nodes i.e., 10 and 12., , Scanned with CamScanner

Page 4 :
Now,, , , , , , , , , , 10, , , , , , ie., elements in the list are, , 15, 22, 15, 25., , Fig. 8.60., , , , , , , , Step 4: Taking two minimum weighted nodes Le., 15 and 15, , Now,, , , , , , , , , , Le., elements in the list are, , 30, 22, 25,, , , , , , , , , , , , , , , , , , , , , , , , , , , , 10, , , , , , 12, , , , , , Fig. 8.61., , , , , , , , , , Step 5: Taking two nodes with minimum weights which are 22 and 25., , 22, , 47, , , , , , 10, , , , , , , , 12, , , , , , 25, , Fig. 8.62., , Now the elements in the list are 47 and 30, , , , , , Scanned with CamScanner

Page 5 :
=, , i jzhts which are 30 and 47., Step 6: Taking two nodes with minimum weights which are 30 and, , 77, , 47 30, , , , , , , , , , , , , , 22 25 | | 15 15, , , , , , 10 12 r 8, , , , , , , , , , , , , , , , , , , , , , , , , , , , , , Fig. 8.63 Huffman Tree, , 8.14.1 Application of Huffman Algorithm, , The Huffman algorithm is used to perform the encoding and decoding of a long message, consisting of a set of symbols. Suppose we want to send a message there are two options, either it sends data as fixed size or to send it as variable length size., , Suppose a collection of n data items Aj, Ag, ....., A,; are to be coded by means of strings, of bits. One way to do this is to code each item by an r-bit string where,, , gn-le n<ar, , E.g., a 48-character set is frequently coded in memory by using 6-bit strings. One cannot, use 5-bit strings since 2° < 48 < 2°., , Suppose the data items do not occur with the same probability. Then memory space may, be conserved by using variable-length strings, were items which occur frequently an assigned, shorter strings and items which occur infrequently are assigned longer strings., , Now, we discuss a coding technique using variable-length string that is based on the, Huffman Tree for weighted data item., , A Huffman tree has to be constructed to perform both encoding and decoding. The, Huffman tree has to be constructed to perform both encoding and decoding. The Huffman, , tree is constructed based on the frequency of the symbols of a given message. The main aim, of using the Huffman algorithm is to minimise the length of the encoded message by assigning, a shorter bit string to the frequently occurring symbols in the message., , Algorithm, , 1. Accept the total number of symbols, say n., , 2. Accept the n different symbols ana their frequencies., 8. Accept the message to be encoded., , 4. Find the two symbols from the given set of symbols such that they occur less frequently., , Scanned with CamScanner