Page 1 :
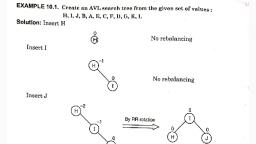
— 10.5 INSERTION IN AN AVL SEARCH TREE, , We can insert a new node in an AVL tree by finding its appropriate position similar to that, of the binary search tree. But insertion of a new node involves certain overheads since the tree, may become unbalanced due to the increase in its height., , 1. If the data item with key ‘k’ is inserted into an empty AVL tree, then the node with key, ‘¥ is set to be the root node. In this case, the tree is height balanced., , , , Scanned with CamScanner
Page 2 :
2. Iftree contains only single node, i.e., root node, then the insertion of the node with key’, depends upon its value. If the value of ‘k’ is less than the key value of the root then it ig, inserted to the left of the root otherwise right of the root. In this case the tree is height, , balanced., 3. Ifon inserting the node with key ‘k’ the height of the right sub-tree of the root has increased,, , |, , -1, , het h+2, , , , , , Fig. 10.6., , In this case, the problem can be easily rectified by rotating node Q about its parent P, so, that the balance factor of both P and Q becomes zero, i.e.,, 2, , , , Fig. 10.7., , Scanned with CamScanner
Page 3 :
In this case, insert a node in the left sub-tree of the right child, i.e.,, -2, , , , Fig. 10.8,, , 4, Ifon inserting a node with key ‘k’, the height of the left sub-tree of the root is increased, ie,, , (a) Height of the right sub-tree of the left sub-tree of the root node is increased, i.e.,, , , , Fig. 10.9., (b) Height of the left sub-tree of the left sub-tree of the root node is increased, i.e.,, , , , Fig. 10.10., 10.5.1 AVL Rotations, , In order to balance a tree, there are four cases of rotations, such as:, LL Rotation, , Inserted node is in the left sub-tree of left sub-tree of node., RR Rotation| Inserted node is in the right sub-tree of right sub-tree of node., Inserted node is in the right sub-tree of left sub-tree of node., Inserted node is in the left sub-tree of right sub-tree of node., , , , , , , , LR Rotation, |RL Rotation, , , , , , , , , , , , Scanned with CamScanner
Page 4 :
is i in the left sub-tree of left sub-tre,, i : The new node x is inserted in ell eof A, h o. - cofemennne +2 after insertion. T'o rebalance the search tree, itis Totated #0 ag, whose balan, , low B to be the root with B,, and A as B, is the teft sub-tree and A is the right sub-tree and, Bada to be the left and right sub-trees of A., , +1, , +2, , , , Insert node x 1, , An into BL, het } h, x, , Ba, , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , B,, Unbalanced AVL search Tree, , After LL rotation, , , , , , , , , , , , , , , , , , , , , , Fig. 10.11, Unbalanced AVL Search Tree., , (Here A, : Right subtree of A, B, : Left subtree of B, Ba : Right sub-tree of B), Le., in LL Rotation, , Left (A) © Right (B), Right (B) — A, , , , , , , , , , Example : Insert node 10, in, , , , Scanned with CamScanner
Page 5 :
——, LL-Rotation, , , , Balanced AVL Search tree, , , , Fig. 10.12., (b) RR Rotation, , Unbalance occurred due to the insertion in the right sub-tree of the right child of the pivot, , node. So, in this rotation new node is inserted at the right sub-tree of the right sub-tree of root, node (pivot node)., , Fig. 10.13 illustrates the balancing of an AVL search tree using RR rotation. Here the new, , node x is in the right sub-tree of A. The re-balancing rotation pushes B upto the root with A as, , its left child and B, as its right sub-tree and A, and B, as the left and right sub-trees of A., -1, , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , A, , 4 $ Insert x, h B into Ba ', t — h, , AL + 4 ‘, , hy - h, y ’ _, BL BR ~, Balanced AVL tree B, *, Unbalanced AVL Tree, 0 :, ‘ RR rotation, |, 4 hei, : |, , y, AL B, Ba, Balanced AVL Search tree after rotation., Fig. 10.13., ~ Thatis, in RR rotation, Right (A) < left (B), left (B) —A, De:, , Scanned with CamScanner