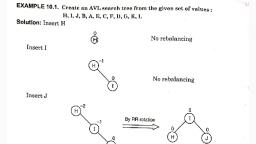
Page 1 :
== SC EMITATION AC AIDINA BC SRS, 1.8.4 REPRESENTATION OF A BINARY TREE, ee, Binary tree can be represented in any of the following two ways:, , 1. Using an array (Linear representation), , 2. Using a linked list (Link representation), , 1 Array Representation: A binary tree can be stored represented using an array,, which is called sequential representation (array representation). This type of representation, jsstatici.e., a block of memory for an array is to be allocated before going to store the actual, tree in It., , In this representation, the nodes of the tree are stored level-by-level, starting from the, oth level. The root node of the tree is stored in the first memory location of allocated memory., The following rules are used to decide the location of any node., , , , 1. The root node is at location 1., , 2. For any node with index i, 1 <i<n., (a) Parent (i) =Li/2], (b) Left child = [i] = 2i, (c) Right child [i] = 21+ 1., , For example: The array representation of the binary tree., , , , , , , , , , , , Scanned with CamScanner
Page 2 :
is, , 1 2 3 4 5 6 8 9 10, , , , , , , , , , , , , , , , , , ¢, B c}]D/E G]H i, , , , , , , , A, , , , , , GBTU (B.Tech) 2945, , Advantages, , 1., 2., 3., , 4,, , Data are stored without any pointer to its successor or ancestor., Any node can be accessed from any other node by calculating the index., Programming languages which do not support dynamic memory allocation, use only, , this type of representation for a tree., , Simplicity., GBTU (B.Tech) 201;, , Disadvantages, , a, , 2., 3., 4,, , Array representation is not suitable for normal binary tree but it is only ideal for complete, , binary tree., Here most of the array entries are empty i.e., unnecessarily more memory is wasted, , There is no way possible to enhance the tree structure., Additions and deletions of nodes are inefficient because of the data movements in the, , array., , To overcome all these problems by using linked list representation., , Scanned with CamScanner
Page 3 :
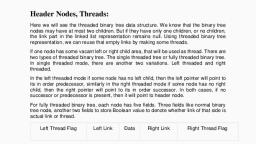
2. Linked Representation of a Binary Tree: The binary tree can be represented, using dynamic memory allocation of a node in a linked list form. In a linked list allocation, technique a node in a tree contains three fields:, , 1. Info (data): It contains the info value., 2. Left link (left): It contains address of the left sub-tree., 38.. Right link (Right): It contains address of the right sub-trees., , , , Left Info Right, , , , , , , , , , , , when a node has no children, the corresponding pointer field are NULL., , (a) A, ? B \ NuLL | oc | NULL, (8) ©), , Lo \, , (0) (€) Nut | pb) | NULL NULL | = | NULL, , Fig. 8.10. Linked representation of a binary tree., , In this, we should declare structure for tree node., struct node, , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , {, int info;, struct node *left;, struct node *right;, }, , , , Scanned with CamScanner
Page 4 :
Here first member info is for information field of node, second member is for left chid of, node which points to the structure itself, it contains the address of left child. If node has no, left child then it should be NULL. Third member is for right child of node which also points, io the structure itself, it contains the address of right child. If node has no right child it, should be NULL., , This type of representation is dynamic i.e., block of memory required for the tree need, not be allocated before. They are allocated only on demand., , Advantages, 1. Insertions and deletions involve no data movement., , 2. No wastage of memory., 3. Enhancement of the tree is possible., , Disadvantages ;, 1. In this, pointer fields are involved which occupy more space than just data fields., , 2. Programming languages which do not support dynamic memory allocation have difficulty, , in implmenting the binary tree., , Scanned with CamScanner
Page 5 :
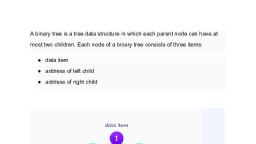
_, 18.5 TYPES OF BINARY TREE, , Atree is a binary tree if and only if: ., 1. It has a root node, which may not have any child nodes (0 child nodes, NULL tree)., , 2. Root node may have 1 or 2 child nodes. Each such node forms a binary tree itself., , 3. Number of child nodes can be 0, 1, 2, ..... not more than 2., , 4, There is a unique path from the root to every other node., , s&h, , Fig. 8.11., , Abinary tree is a stri i ; ., odes or no modoc a strictly binary tree if and only if each node has exactly two child, , ey, AR, , Fia. 8.12, , Scanned with CamScanner