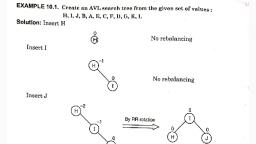
Page 1 :
Formally, a tree can be defined recursively in the following manner., 1. Asingle node by itself is a tree. This node is also the root of the tree., , 2. Suppose nis a node and T,, T,, ..., T,, are trees with roots nj, No, ..., Ny, respectively. We, can construct a new tree by making n be the parent of nodes, n,, ng, ..., n,. In this tree, , nis the root and T,, Ty, ..., T,, are the swb-trees of the root. Nodes n,, Ng, ..., Ny are called, the children of node n., , Scanned with CamScanner

Page 2 :
Examples of Trees, , (a), , (a) is an empty tree, , () (e), , (f), , (b), , (9), , Scanned with CamScanner

Page 3 :
A binary tree is either empty, or it consists of a node called the root together with two, binary trees called the left sub-tree and the right sub-tree of the root. The definition, of a tree does not impose any combination on the number of children of a given node., , This number can vary from 0 to any integer., , Scanned with CamScanner

Page 4 :
— 8.2 TERMINOLOGIES USED, , 1. Node: We will use the term node, rather than vertex, with binary tree. This is the main, component of any tree structure. It stores the actual data along with linkes to other, nodes. Fig. shows the structure of a node., , Scanned with CamScanner

Page 5 :
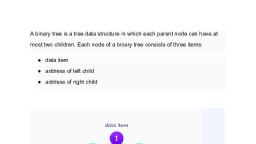
reer, , , , , , , , DATA, , , , , , , , Left Child Right Child, , Fig. 8.2., , 9, Parent: The parent of a node is the immediate-predecessor of that node. In Fig. Ais the, parent of nodes B and C,, , , , , , , , , , , , , , , , , , , , , , , , rie ly rlely, , Fig. 8.3., , 3. Child: The immediate successors of a node are called child nodes. A child which is, placed at the left side is called the left child anda child which is placed at the right side, is called the right child. In the above, Fig. B and C are the child nodes of A., , 4. Root: A root is a specially designated node in a tree. It isa node which has no parent., There can be only one root in a tree. In Fig. 8.4, the node Ais the root of the tree., , , , , , , , , , , , , , , , Fig. 8.4., , 5. Leaf Node (External node): A leaf node which does not have any child node. In Fig., 8.4 nodes D, E and F are leaf nodes., , 6. Siblings: The child nodes of a given parent node are called siblings. In the Fig. 8.4, D, and E are siblings., , 7. Branch or Edge: It is a connecting line between two nodes. A node can have more, than one edge. In Fig. 8.4, the node A has two branches. Actually, a branch is a pointer, to a node in the tree., , 8. Path: Each node has to be reachanable from the root through a unique sequence of, edges calied a Path. The number of edges in a path is called the length of path., , Scanned with CamScanner