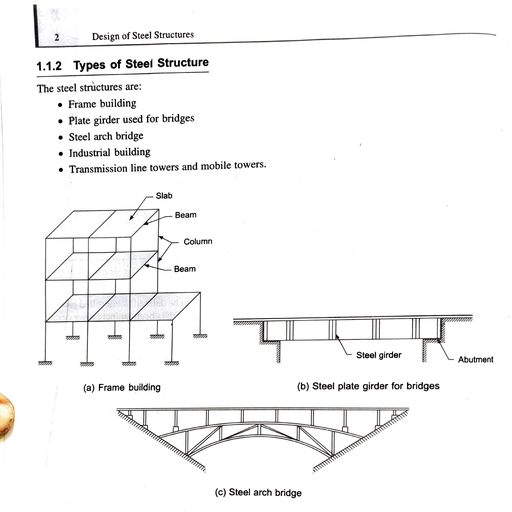
Page 1 :
Limit, , State of, , Collapse:, , Flexure, , SOLVED EXAMPLES, Eramples, , on, , Determining the, , Depth of Neutral Aris, , with, 400 mm, reinforced, neutral axis of a beam 250 mm x, of, 415 steel., the depth, Example 4.1. Determine, M 20 concrete and Fe, Also check for the type of section. Use, diameter., For M20 concrete], hars of 20 mm, Solution. Given:, , S, , 20 N/mm?, , For Fe 415 stel], , S 415 N/mm, , b, d, , 250 mm, 400 mm, , Ag 3xx20=942.5 mm, Depth of neutral, , axis (r), , 0.87 0.87 f, A, , 0.36 fck bd, 0.87 x 415 x 942.5, , d, , 0.36 x 20x 250x 400, 0.4725, , =, , 189 mm, , axis depth (r, max, Limiting value of neutral, umax = 0.48, , d, x, u max= 0.48, XXumax, , 400, , =, , From Table 4.2], , 192, , mm, , The beam is under-reinforced., Examples on, , Moment, , Beam, of Resistance of Singly Reinforced, , beam of dimension 250 mm x 350 mm., moment of resistance of a, the, 4.2., Determine, Example, at a distance of 40 m m from bottom of, mm diameter placed, area of steel consists of 3 bars of 12, The, , beam. Use M20 and Fe 415 steel., , Solution. Given:, , b, , 250 mm, , d, , 350-40 3 1 0 mm, , A,, , =, , Jok, , S,, , 3xx 122, , =339, , mm2, For M20 concrete], For Fe 415 steel], , 20 N/mm, =, , 415, , N/mm, , Depth of neutral axis (r), 0.87 S, A0.87 x 415 x 339, 0.36 fe b, X, , =, , 68 mm, , 0.36, , x, , 20 x 250

Page 2 :
102, , Reinforced Cement Con., , Conctele De, , birc, , A, , axis), limiting depih of neutral, , 48 d, , From 'Table a, , (0.48 x 310, , 148.8 mn>68 mm, max, , henee, , it is an under-reinforeed section., , Moment of resistanwe (M,), , M0.87/,A,(d-0.42 ), 0.87 x 415 x 339 (310- 0.42 x 68), 34447116.16 Nmm, , M,, , 34.44 kN, , =, , mm., , Example 43 Determine themoment ofresistanceof the beam having dimension.as3, , effective. The beam is reinforced with 1963 mm of steel in the tension zone. Use, Fe 415 stee. Abso comment on the design of beam., , Solution. Given:, , b, , 550 :me, M20 concrete, , 300 mm, , d = 550 mm, , A, , 1963 mm, , S, , = 415 mm, , S, , = 20 N/mm*, , Depth of neutral axis (r), , 0.36, , 0.87 f, A, , fkb, , 0.87 x 415 x 1963, 0.36 x 20 x 350, , Limiting depth, , 326.3, , mm, , of neutral axis, r,, max0.48d, , From Tabie, , 0.48 x 550, , umax, , 263.5, , =, , mm <, , x,, , u mar, , Hence the section is over, , reinforced and the, , Moment of resistance (M,), , moment of, , resistance of such section is equal, , m a u 263.5 mm, , M., , =, , 0.36fbx ma (d-0.42x, max, 20, , 0.36, , x, , 25047, , x, , x, , 300, , x, , 263.5, , 10° Nmm, , (550 0.42 x, , 263.5), , M, = 250.47 kNm, , Comment: The beam is over, such beams is sudden and, without, , reinforced, , waning., , and, , hence it should be, , redesigned be, , to ,, , is

Page 3 :
Limit, , State of, , 103, , Collapse Flexure, , Example, , 4.4. Solve the, , Example, , 4.3. If steel used is Fe 250., , 2.50, , Solutlon., iiven:, , IFor Fe 250 steel, , N/mm*, , Depth of neutral axis (r,), , 0.87 /y A, , 0.360.36 f.b, 0.87 x 250x 1963, , 0.36x 20 x 300, , 196.6, , mm, , Limiting depth of neutral axis (r, ma), , From Table 4.2, , u maO.53 d, = 0.53 x 550, , = 291.5 mm, section is under-reinforced., m a t e hence the, , Moment ofresistance (M), M, =, , 0.87 s, A, (d - 0.42 x ), , = 0.87 x 250 x 1963 (550 - 0.42x 196.6), , 199.6x 10" Nmm, , M,, , =, , 199.6 kNm, , Example 45. Areinforced concrete slab 150mmthickisreinforced with 10 mm bars @180 mm cle, The reinforcement is located at an effective depth of 125 mm from top. Calculate the moment of resistance, of the section. Use M20 concrete and Fe 415 steel., D = 150 mm,, , Solution. Given:, , d, , 125 mm, , Sk 20 N/mm, S = 415 N/mm, , A calculation, Area of one bar = x10 = 78.5 mm2, 1000x 78.5, , A,, , 180, = 436.1 mm*, , Depth of neutral axis (r,), , 0.87 ,.A, 0.36 S, , b, , 0.87 x 415 x 436.1, , 0.36 x 20x 1000, , 21.86, , mm., , IConsidering 1 m width of slabl

Page 4 :
104, , Reintorced Cement, , Limitine depth of newtral axs, 048, , d, , From Table A, , = 0.48 x 125 = 60 mnm, , hence, , Corcrete, , the siab is under-reinforoed, M, =0.87, A,td-0.42 x), = 0.87 x 415 x 436.l (125 0.42 x 21.86), = 18236122.33 Nmmn, , M. 18.23 kNm., Bxemple 46 An R.C.C. beam,200, bars ef Fe 415 steel. Find the ultimate, aqf5m. Take M20 concrete., , Solution. Given:, , b, , 400 mm (effective), is reinforced with 3-16 mm, uniformly distributed load which the beam can carry sal, mmx, , 200 mm, d=400 mm, , A 3xx16 =603.19 mm, Ja = 20 N/mm, , S,, , =, , 415, , For M20 concrete, , N/mm, , For Fe 415, , L = 5m, , concre, , Depth of neutral axis ), 0.87 ,A, , 0.87x 415 x 603.19, , 0.36 fa.b, , 0.36x 20x 200, , X, = 151.2 mm, , Limitinmg depth of neutral axis ,, , m, , max0.48 d = 0.48 x 400, , [From Table 4, , = 192 mm, , m c , hence the section is under-reinforced., Moment of resistance (M,), M. = 0.87 S,.A, (d-0.42 x,), , 0.87 x 415 x 603.19 (400 0.42, M = 73.28 x 10° Nmm, =, , x, , 151.2), , M. 73.28 kNm, , Ultimate load (w), Equating maximum factored bending moment and the ultimate moment of resistance., Max. moment, M =, , x12, 8, , M M., , w X, 8, , =, , 73.28, , w 23A5 kN/m

Page 5 :
Limit State of Collepse:, , 105, , Flexure, , Example 4.7. A rectangular beam is 20 cm wide and 40 cm deep upto the centre of tefnforcement., FYnd the area of reinforvement required if it has to resist a moment of 25 kNm. Use M20 concrete mix, , and Fe 415 steel., Solution. Given:, , b, , 20 cm = 200 mm, , d, , 40cm = 400 mm, , M, , 25 kNm= 25 x 10° Nmm, , S, , 20 N/mm, , For M20 concrete), , = 415 N/mm?, , For Fe 415 concrete), , Factored bending moment, = Yx BM, , = 1.5 x 25 x 10°, , IY= Load factor = 1.5], , 37.5x 10° Nmm, Factored BM = Moment of resistance, , 37.5, , A, , x, , M,, , =, , M,, , =, , 10=, , (400-0.10375 A,), , A-3855.4 A, +1001096.192, , JyAs, , 0.87/,A,", 0.87x415, , x, , 0.87 x 415, , x, , =, , 103863.73, , =, , 0, , fabd, A,, , x4001, , 400 x, , 415A, , 20x, , 200x 400, , 415A, A |1-20x 200 x 400, , 3855.4 t(3855.4) - 4x 1001096.192, , A, , 2, , As 280 mm, Depth of neutral axis, 0.87 y.Ag, , 0.360.36 ft .b, , 0.87x415x280, 0.36 x 20x 200, = 70.2 mm, , Limiting depth of neutral axis, = 0.48 d = 0.48 x 400, , Xu max=192 mm>r,, , a mx, , hence the section is under reinforced and design is OK.