Page 1 :
REFLECTION OF LIGHT BY PLANE SURFACES

Page 2 :
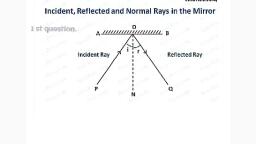
We have learnt about shadows and we carried out many experiments with light rays and also discussed the rectilinear propagation of light i.e., light travels in a straight line. In class 7 we learnt the laws of reflection., Let us recall some of them., A source of light, an opaque object and a screen are needed to form a shadow., Light travels in a straight line., When light gets reflected from a surface, the angle of reflection is equal to the angle of incidence., The incident ray, the normal at the point of incidence and the reflected ray all lie in the same plane., We observed shadows and images in your daily life. Some questions might have come to your mind while observing these shadows or images.

Page 3 :
How can we get the image of a big building in a small mirror?, Can we get the image formed by a plane mirror on a screen?, Why is there right-left inversion when we look into a mirror?, Why is the angle of reflection equal to the angle of incidence when a light ray gets reflected from a surface., In this lesson we are going to learn about reflection of light on plane surfaces in detail so that we can answer the above questions., Let’s start with some activities based on your previous knowledge., Formation of image by a pinhole camera, Recall how an image forms in a pinhole camera that you have learnt in class 6., Draw a ray diagram of the formation of an image in a pinhole camera.

Page 4 :
What would happen if we increase the size of the hole of the pinhole camera. Observe the flame of a candle with a pinhole camera making a big hole., , , , , , , Try to draw a ray diagram of the formation of an image in a pinhole camera with a big hole., By observing the figure we can understand that the light rays coming from the top of the candle flame fall at different points on the screen., Similarly the rays coming from bottom of the candle flame also fall at different points on the screen., Thus we get blurred image on the screen due to the big hole of the camera.

Page 5 :
Activity , A smart crow is on a tree at point ‘A’ as shown. Some grains are on the ground., If the crow wants to take a grain and reach the point ‘B’ on the other tree as early as possible(in least time), from where should the crow pick up the grain., Which among the paths ACB, ADB, AEB and AFB is the shortest path?, To compare the lengths of these paths, we make duplicates of them in such a way that all the duplicate paths meet at point G as shown in figure.

Page 6 :
In the figure, CB = CG. The length of path ACB = AC+CB = AC+CG = ACG., The length of the path ACG is equal to the length of the path ACB. similarly ,, length of the path ADB = length of the path ADG, length of the path AEB = length of the path AEG, length of the path AFB = length of the path AFG, If you observe Fig carefully, you will notice , that, among the paths ACG, ADG, AEG and AFG,, the shortest path is AEG, because it is the straight , line distance between points A and G. , we can measure and check this using a scale. , AEG=AEB, path AEB is the shortest path , to reach point B from point A., It would take the least time. So the smart , crow will pick the grain from point E., Observe the path AEB once again in figure.

Page 7 :
This principle was given by Pierre de Fermat, a French lawyer and mathematician., It is also applicable to reflection of light. , When light gets reflected from a surface, it selects the path that takes the least time. That is why the angle of incidence is equal to the angle of reflection.