Page 1 :
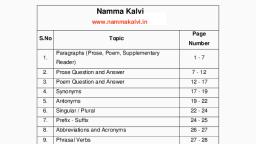
CONTENTS, Sl.No., , Chapters, PART - 1, , 1, , Number Systems, , 2, , Introduction to Euclid’s Geometry, , 3, , Lines and Angles, , 4, , Polynomials, , 5, , Triangles, , 6, , Constructions, , 7, , Quadrilaterals, , ♦, , Appendix - 1, , PART - 2, 8, , Heron’s Formula, , 9, , Coordinate Geometry, , 10, , Linear Equations in Two Variables, , 11, , Areas of Parallelograms and Triangles, , 12, , Circles, , 13, , Surface Areas and Volumes, , 14, , Statistics, , 15, , Probability, , ♦, , Appendix - 2, , ◘, , Model Question Paper, , Pg.No.

Page 2 :
CHAPTER - 1, , Number System, Key Points :, , ●●, ●●, , Number System : A system in which we study different types of numbers, their relationship, and rules govern in them., In the Hindu-Arabic system, we use the symbols 0,1,2,3,4,5,6,7,8 and 9. These symbols are, called digits., , Types of Numbers, , 1. Natural numbers : Natural numbers are counting positive numbers. They are denoted by N., Ex : N = {1,2,3,......}, 2. Whole numbers : All natural numbers and zero form the set of whole numbers. Whole numbers, are denoted by w., Ex : w = {0,1,2,......}, 3. Integers :Whole numbers and negative numbers form the set of integers. They denoted by I or Z., Ex : I = {0,±1, ±2, ±3.......}, i. Positive integers : Natural numbers are called positive integers. They denoted by I+ (or) Z+ ., Ex : I+ = {1,2,3,....}, ii. Negative integers : Negative numbers are called negative integers. They denoted by I, Ex : I = {–1,–2,–3,......}, 4. Even numbers : A counting numbers which are multiples of 2 is called even number., Ex : 2,4,6,8,......, 5. Odd numbers : A counting numbers which are not multiples of 2 is called odd number., Ex : 1,3,5,7....., 6. Prime numbers : A numbers which are divisible by 1 and itself having only two factors is called, prime numbers., Ex : {2,3,5,7,11...}, 7. Composite numbers : A numbers which having more than 2 factors is called composite numbers., Ex : 4,6,8,9....., 8. Co prime : Two natural numbers are said coprime if their HCF is one, Ex : (8,9) (10,15), 9. Rational numbers : A number that can be expressed in the form p/q is called rational numbers., Where p and q are integers and q ≠ 0., Ex : 3/5, 8/3, 7/9 ....., OR, The decimal expansion of an rational number is either terminating (or) non-terminating recurring., 10. Irrational number : The number that cannot be expressed in the form of p/q are called irrational, numbers (or), The decimal expansion of an irrational number is non - terminating non - recurrins is called, irrational number.

Page 3 :
2, , IX Standard – Mathematics, Ex: 3 , 3 , 7 ...., , 11. Real numbers : The set of both rational and irrational numbers is called real numbers. They are, denoted by R., Ex:R = 2 , 2, 3...., 9, , {, , ●●, ●●, ●●, , }, , There is a unique real number corresponding to every point on the number line. Also, corresponding to each real number, there is a unique point on the number line., If r is rational and s is irrational, then r + S and r-S are irrational numbers, and rs and r/s are, irrational numbers r ≠ 0, For positive real numbers a and b, the following identities hold, i. ab = a b, ii., , a, =, b, , a, b, , ( a + b )( a − b ), iv. ( a + b )( a − b ) =a − b, v. ( a + b ) =, a + 2 ab + b, vi. ( a − b ) =, a − 2 ab + b, vii. ( a + b )( c + d ) = ac +, iii., , 2, , 2, , 2, , ●●, ●●, ●●, ●●, , ●●, , ad + bd, , Rationalization : The process of multiplying by another irrational number is called, rationalization., The product of two irrational numbers is rational each irrational number is called rationalizing, factor., Rationalizing factor of an a monomial irrational number is same irrational number., Rationalizing factor of an a binomial irrational number is conjugate of an binomial irrational, number., 1, Ex:, Rationalizing factor is a − b, a+ b, Let a > 0 be a real number and p and q be rational numbers then, ii. ( a p ) = a pq, q, , i.a p .a q, , ap, p−q, =, iii. q a=, iv.a p b p, a, p, , ap  a , o, =, üüüp =, , b, b, 1, vii.a − n = n, a, , ( ab ), , p

Page 4 :
3, , Chapter 1 – Number System, Exercise 1.1, , 1., , Is zero a rational number? Can you, p, write it in the form, , where p and q, q, , are integers and q ≠ 0?, Ans. Yes, zero is a rational number and it can be, p, written in the form of ., q, \ 0=, , 0, , where =, p 0 ,q ≠ 0, 2, , 2., , Find six rational numbers between 3, and 4., Ans. 3 and 4 can be written as, 3 4, &, 1 1, Multiply both numerator and denominator, of the rational number by 7, 3 7, 4 7, \ × & ×, 1 7, 1 7, 21, 28, and, 7, 7, \ Six rational numbers between 3& 4 are, 25, 26 24, 27 26, 28 29, 22 23, 27 30, , &, , ,, ,, &, 78 78 78 78 87, 8, 3., , Find five rational numbers between, 3, 4, and, 5, 5, , Ans. Five rational numbers between, 3, 4, and, 5, 5, 3 6 18, 4 6 24, =, ×, & =, ×, 5 6 30, 5 6 30, , \ Five rational numbers between 3 & 4, 5, 5, 19 20 21 22, 23, , , , and, 30 30 30 30, 30, , 4., , State whether the following statements, are true or false. Give reasons for your, answers., , i. Every natural number is a whole, number., ii. Every integer is a whole number, iii. Every rational number is a whole, number., Ans. i. True, because set of whole numbers, contains natural numbers., ii. False, because whole numbers does not, contains negative integers., iii. False, because whole numbers not, in the form of p/q and it is not contains, negative integers., Exercise 1.2, , 1., , State whether the following statements, are true or false. Justify your answers., i. Every irrational number is a real, number., ii. Every point on the number line is of, the form m , where m is a natural, , number., iii. Every real number is an irrational, number., Ans. i. True, since collection of real numbers is, group of rational and irrational number., ii. False, no negative number can be the, square root of any natural number., iii. False, for example 5 is real number but, not irrational number., 2., , Ans., , Are the square roots of all positive, integers irrational? If not, give an, example of the square root of a number, that is a rational number., No, for example 36 = 6is a rational number., , 3., , Show how, , Ans., , 5 can be represented on, the number line., =, 5, , ( 2 ) + (1), 2, 2, ( 2 ) + (1), , 5, =, =, 5, , 4 +1, 2, , 2

Page 5 :
4, , IX Standard – Mathematics, B, 5, A P, 2, 3, , 1, , –3 –2 –1 0, , P5, , In right angle ∆ le OBC A =, 90o, 2, , OB, = OA + AB, =, , ( 2), , 2, , + (1), , 3, , 5, , 2, , 1, , 0, , 2, , Exercise 1.3, , 1., , OB2 = 5, , Write the following in decimal form, and say what kind of decimal expansion, each has :, , OB = 5, \ OB = OP = 5, Classroom activity (Constructing the, ‘square root spiral’) : Take a large sheet, of paper and construct the ‘square root, spiral’ in the following fashion. Start, with a point O and draw a line segment, OP1 of unit length. Draw a line segment, P1P2 perpendicular to OP1 of unit, length. Now draw a line segment P3P4, perpendicular to OP2. Continuing in this, manner, you can get the line segment, Pn-1 Pn by drawing a line segment of unit, segment OPn-1 . In this manner, you will, have created the points P2 , P3 ...., Pn ......, , and joined them to create a beautiful, spiral depicting 2, 3 , 4 ,...., P2, 1, P3, P1, 3, , Ans., , 4, , 2, , OB2= 4 + 1, , 4., , P1, , P4, , 5, 2, , P2, , P3, , 2, , 36, 100, , i., Ans., , 36, = 0.36, 100, It is a terminating decimal., 1, 11, , ii., Ans., , 1, = 0.0909, = 0.09, 11, Which is non-terminating, decimal., , iii., Ans., , 1, , 0, iv., Ans., , 4, , 1, 8, , 1 33, 4= = 1.125, 8 8, \ It is a terminating decimal, , 3, 13, 3, = 0.2307692...., 13, = 0.230769, , repeating

Page 6 :
55, , Chapter, Chapter 11 –– Number, Number System, System, 13)30(.2307692, 26, 40, 39, 100, 91, 90, 81, 90, 78, 120, 117, 30, 26, 4, Which is non - terminating repeating, decimal., 11)20(.1818, 11, 90, Ans., 88, 2, 20, = 0.1818..., 11, 11, =2 0.18, 90, = 0.1818..., 11, Which is non − terminatinf repeating88, = 0.18, 2, decimal, Which is non − terminatinfg repeating, decimal, , v., , vi., Ans., , 2., , [Hint : Study the reminders while, finding the value of 1/7 carefully], Ans. Yes, we can predict the decimal expansions, of 2/7, 3/7, 4/7, 5/7, 6/7 without actually, doing the long division., 1/7 =, 1)10(.1428571, , 1, 0.1428572, \ =, 7, 2, 1, \ = 2 × = 0.285714, 7, 7, 3, 1, =3 × =0.428571, 7, 7, 4, 1, = 4 × =0.571428, 7, 7, 5, 1, =5 × =0.714285, 7, 7, 6, 1, =6 × =0.857142, 7, 7, , 2, 11, , 329, 400, 329, = 0.8225, 400, Which is terminating, , You know that, , 400)3290(.8225, 3200, 900, 800, 1000, 800, 2000, 2000, 0, , 1, = 0.142857. Can you, 7, , predict what the decimal expansions, 2 3 4 5 6, of, , , , ,, are, without actually, 7 7 7 7 7, doing the long division? If so, how?, , 7, 30, 28, 20, 14, 60, 56, 40, 35, 50, 49, 10, 7, 3, , Then the new quotient beginning from, there digits using the repeating digits, 1,4,2,5,7,8., 3., , Express the following in the form p/q,, where p and q are integers and q ≠ 0., –, i., 0.6, –, Ans. i. 0.6, Let x = 0.666 ...., Multiply both side by 10, 10x = 6.666....., 10x= 6 + 0.6666....., 10x= 6 + x, 10x − x =, 6, 9x = 6, =, x 6= 2, 9, 3, 2, \ 0.6 =, 3, Where p= = 22and, Where, andq=q =3 (3≠ 0 ), –, ii. 0.47, –, Ans. 0.47, x = 0.4777........, Multiply 10 both sides

Page 7 :
6, 6, , IX, IX Standard, Standard –– Mathematics, Mathematics, 10x = 4.777...., 10x = 4 + 0.777..., 10x = 4.3 + 0.4777..., 10x = 4.3 + x, 10x-x = 4.3, 9x = 4.3, 4.3 43, =, x =, 9, 90, – 43, 0.4, 04.77 =, 90, Where, =, p 43&, =, q 90, , Ans., , 1, = 0.0588235294117647, 17, \ After16 digits decimal part is repeating., , 4., , 5., , What can the maximum number of, digits in the repeating block of digits in, , 1, 17, 17 100 0.0588235294117647, 85, 150, 136, 140, 136, 40, 34, 60, 51, 90, 85, 50, 34, 160, 153, 70, 68, 20, 17, 30, 17, 130, 119, 110, 102, 80, 68, 120, 119, 1, , iii. 0.001, Ans., 0.001, Let x = 0.001001001......., Multiply both sides by1000, 1000x = 1.001001......, 1000x = 1 + 0.001001....., 1000x = 1 + x, 1000x − x =, 1, 999x = 1, x= 1, 999, \=, p 1&=, q 999, Express 0.99999....in the form p/q. Are, you surprised by your answer? With, your teacher and classmates discuss, why the answer makes sense., Ans. Let x = 0.9999....., Multiply by 10, 10x = 9.9999...., 10x = 9 + 0.999...., 10x = 9 + x, 10x - x = 9, 9x = 9, =, x 9= 1= 1, 9, 1, Since 0.9999.... goes for ever, so there is, no gap between 1 and 0.9999....end hence, they are equal., , the decimal expansion 1/17? Perform, the division to check your answer., , 6., , Look at several examples of rational, numbers in the form p/q (q≠0), where, p and q are integers with no common, factors other than 1 and having, terminating decimal representations, (expansions). Can you guess what, property q must satisfy?, Ans. Examples :, 5 5, = 0.5, |q= 2, (i ) 12 = 12 × =, 5 10, 1 25 25, ( ii ) 1 4 = × = =0.25 | q =22, 4 25 100, 3 3 125 375, 0.375 | q =, 23, ( iii ) =× = =, 8 8 125 1000, 31 31 4 124, = 1.24 | q = 52, ( iv ) = × =, 25 25 4 100, 13 13 5 65, =, × =, = 0.65, | q = 22 × 51, 20 20 5 100

Page 8 :
1 × 5 = 5 = 0.5, 2 5 10, 1 25 25, ( ii ) 1 4 = × = =0.25, 4 25 100, Chapter, 3 –– Number, 3 125 System, 375, Chapter 1, 1, Number, System, 0.375, ( iii ) =× = =, 8 8 125 1000, 31 31 4 124, = 1.24, ( iv ) = × =, 25 25 4 100, 13 13 5 65, =, × =, = 0.65, 20 20 5 100, , (i ) 12 =, , |q= 2, | q =22, , 7, 7, , |q=, 23, 4.795831523, 4 23, 4 16, 87 700, 7 609, 949 9100, 9 8541, 9585 55900, 5 47925, 95908 797500, 8 767264, 959163 3023600, 3 2877489, 9591661 14611100, 1 9591661, 95916625 501943900, 5 479583125, 959166302 2236077500, 1918332604, 9591663043 31774489600, 28774989129, 2999500471, , | q = 52, | q = 22 × 51, , The property that q must satisfy is that the, prime factorization of q must have only, powers of 2 or powers of 5 or both., 7., , Write three numbers whose decimal, expansions are non-terminating nonrecurring., Ans. 0.020020002..........., 0.023023023......, 3.123123123......, 2.121231234..........., 0.222222......, 0.202002000..........., 8., , Find three different irrational numbers, between the rational numbers, 5, 9, and ., 7, 11, , Thus 23 = 4.795831523....., The decimal expansion is, non − terminating and non − recurring, , Ans., , 7 50 0.714285 11 90 0.8181.., 49, 88, 10, 20, 7, 11, 30, 90, 28, 88, 20, 20, 14, 11, 60, 9, 56, 40, 35, 5, 5, =, Thus, 0.714285..., = 0.714285, 7, 9, = 0.8181...., = 0.81, 11, Three irrational number, 0.742432......., 0.783423......., 0.8080......., 0.808008000..........., , \ 23 is an irrational number, , ( ii ), , 225 = 15, , 225 is a rational number, , ( iii ) 0.3796, The decimal expansion is terminating, \ 0.3796is a rational number, , ( iv ) 7.47478...... = 7.478, The decimal expansion is, non − terminating recurring, \ 7.478478....is a rational number, \7.478478......, , ( v )1.101001000100001...., The decimal expansion is, non − terminating and non − recurring, \ It is irrational number, , 9., , Classify the following numbers as, rational or irrational :, Ans. i. 23, , Exercise 1.4, , 1., , Visualize 3.765 on the number line,, using successive magnification.

Page 9 :
8, , IX, IX Standard, Standard –– Mathematics, Mathematics, , Ans. 3.765, 3 3.1 3.2 3.3 3.4 3.5 3.6 3.7 3.8 3.9 4, 3.7 3.71 3.72 3.73 3.74 3.75 3.76 3.77 3.78 3.79 3.8, , 3.76 3.761, , 3.765, , 3.77, , 2., , Visualise 4.26 on the number line, up to, 4 decimal places., Ans. 4.26 = 4.2626....., 4, , 4.2 4.3, , 4.2, , 5, 4.26 4.27, , 4.26 4.262 4.263, 4.262, , 4.2626 4.2627, , 4.3, 4.27, , v., 2p, Ans. 2 is irrational number and p is an irrational, number., \2p is an irrational number., 2., , Simplify each of the following expressions:, , i., , (3 + 3 )( 2 + 2 ), , Ans., , Exercise 1.5, , Classify the following numbers as, rational or irrational :, , i., , 2− 5, 2 − 5 is an irrational number, \ The difference of rational number and, and irrational number is irrational number, , i., Ans., , (3 +, , 23 − 23, , (3 +, , 23 − 23, , =, 3 + 23 − 23, =3, which is an rational number, iii., , 6+3 2 +2 3 + 6, =, , Ans., , (3 + 3 )(3 − 3 ), (3 + 3 )(3 − 3 ) = (3) − ( 3 ), 2, , 2, , = 9−3, =6, iii., Ans., , (, , 5+ 2, , ), , 2, , (, , 5+ 2, , ), , 2, , 2, ( a + b ) =a 2 + 2ab + b 2, 2, , 2 7, , (, , 7 7, , Ans., 2 7, , (3 + 3 )(3 − 3 ), It is in the form ( a + b )( a − b ) = a 2 − b 2, , ), , ), , (3 + 3 )( 2 + 2 ), 3( 2 + 2 ) + 3 ( 2 + 2 ), 6+3 2 + 2 3 + 3× 2, , ii., , Ans., , 2, , Ans. It is an irrational number., , 4.263, , 1., , 1, , iv., , 2, , ((, , 5, , ), , 2, , +2 5 2+, , =, 5 + 2 10 + 2, , =2, , 7, 7 7, which is a rational number, , ), , 5+ 2 =, , = 7 + 2 10, iv., , (, , 5− 2, , )(, , 5+ 2, , ), , ( 2) ), 2

Page 10 :
99, , Chapter, Chapter 11 –– Number, Number System, System, Ans., , (, , 5− 2, , )(, , 5+ 2, , ), , It is in the form ( a + b )( a − b ) = a 2 − b 2, , (, , 5− 2, , )(, , ) ( 5) −( 2), , 5+ 2 =, , 2, , 2, , = 5−2, =3, 3., , Recall, p is defined as the ratio of the circumference(say c) of a circle to its diameter (say, c, d). That is, p = . This seems to contradict the fact that p is irrational. How will you, d, , resolve this contradiction?, Ans. We know that quotient of a non - zero rational number and an irrational number or quotient of, an irrational number with non-zero rational number is always an irrational number., c, p = .Therefore, there is no contradiction as either ccord, or d are irrational hence, p isan irrational number., d, 9.3 on the number line?, Ans. Steps of construction, 1. Mark the distance 9.3 units from a fixed point A. to, which, is =, from, B. AB, 9.3 B AB = 9.3, 2. From B make distance of 1 unit and mark the new point as C. i.e., BC = 1 unit., 3. Find the midpoint of AC and name it as M., 4. Taking MC as radius and M a as centre draw semicircle., 5. Draw a line perpendicular to AC passing through B and intersecting at D., 4., , Represent, , D, , 3, , 9., , A, , M, , B 1 C 2, , 9.3, , \ BN =, 9.3, MA = MCare radius of semicircle, 5., i., Ans., , Rationalise the denominators of the following :, 1, 7, , 9.3, , 3 N

Page 11 :
7 − 2is 7 + 2, 1, , +2, IX7 Standard, – Mathematics, × IX Standard – Mathematics, 7 −2, 7 +2, , 10, 10, 1, =, 7, , 1, 7, , ×, , 7, , =, , 7, , 7, =, 2, 7, , =, , 7, 7, , ( ), , Rationalizing factor of, 7 − 6 is 7 + 6, , =, =, , 1, 7− 6, , 7+ 6, , ×, , 7+ 6, , 7+ 6, , ( 7) −( 6), 2, , 7+ 6, =, 7−6, , =, , 2, , 5+ 2, , 1, , =, , 5+ 2, =, , 1., , ( 5) −( 2), 2, , 2, , 5− 2, 5−2, 5− 2, =, 3, , Ans. Rationalizing factor of, 7 − 2is 7 + 2, , =, , 7 +2, , ×, , 7 +2, , 7 +2, , ( 7), , 2, , − ( 2), , 7 +2, , =8, , 2, , ii. (32)1/5, Ans. (2 x 2 x 2 x 2 x 2)1/5, , (2 ), 5, , 1, , 5, , 5, n, 5, = 2=, 21 ( a m=, a mn , ), , , =2, , iii., , (125)1/3, , Ans. = ( 53 ), 3, , 1, , 3, , (a ), , m n, , 3, , 2., , Find :, , i., , 93/2, , Ans. ( 32 ), , 7 −2, , 1, , 2, , = a mn, , =5, , 7 −2, , =, , 6× 1, , ( 64 ), , =5, , 1, , 1, , 2, , ( a m )n = a mn , , , 3, = 2 = 2× 2× 2, , =2, , =, , iv., , 1, , 6, , 5− 2, , 5− 2, , Find :, , (2 ), , 5− 2, , ×, , 2, , i., (64)1/2, Ans. (2 x 2 x 2 x 2 x 2 x 2)1/2, , 7+ 6, , Ans. Rationalizing factor of, 5 + 2 is 5 − 2, , − ( 2), , Exercise 1.6, , ( a + b )( a − b ) = a 2 − b 2 , , 1, , iii., , 2, , 7 +2, 7−4, 7 +2, =, 3, , 7− 6, , Ans., , ( 7), , =, , 1, , ii., , 7 +2, , 2, , 3, , 2, , 3× 3, , =3, , = 33, , 2, , ( a m )n = a mn , , , , = 3× 3× 3, = 27

Page 12 :
11, 11, , Chapter, Chapter 11 –– Number, Number System, System, ii. (32)2/5, Ans. (2 x 2 x 2 x 2 x 2)2/5, 2, n, = ( 25 ) 5 ( a m ) = a mn , , , =2, , 5× 2, , ii., , 1, , iii., , i., , 11, 11, , a −1 = 1, , a, , 1, , 2, 4, , = 11, , 1 −1, 2 4, , 2 −1, , = 11 4, , 1, , = 11, , Ans., 2, , 1, , 2, , 1, , 2 3 .2, , 1, , Using the identity, , 2 3 .2 5, 2 3 .2, , 1, , Ans., , Simplify, 2, , 112, 114, , 3, , 1, −1, = 5=, 5, 3., , 1, = a −1, a, , = 3−21, , 4, , iv. (125)-1/3, Ans. (5 x 5 x 5)-1/3, −1, n, ( 53 ) 3 ( a m ) = a mn , −3, , 7, , m, , = 23 = 2 × 2 × 2, =8, , =5, , 1,  3, 3 , , am, a, Using the identity   = m, b, b, 7, n, 1, 1, = 21, ( a m ) = a mn, 3 7, 3, (3 ), , iii. (16)3/4, Ans. (2 x 2 x 2 x 2)3/4, 3, n, ( 24 ) 4 ( a m ) = a mn , 4× 3, , 7, , Ans., , 5, , = 22 = 2 × 2, =4, , =2, , 1,  3, 3 , , iv., , 5, 5, , =2, , 2 +1, 3 5, , am × an =, a m+n, , Ans., , 1, , 4, , 1, , 1, , 1, , 1, , 7 2 .8 2, 7 2.8, , 2, , 10 + 3, 15, , a m .b m = ( a .b ), , 13, 15, , ( 7.8), , =2, =2, , 1, , 2, , = ( 56 ), = 56, , 1, , 2, , 1, , 2, , m, , am, = a m−n, an

Page 13 :
12, , IX Standard – Mathematics, Additional PROBLEMS, , I., 1., , Multiple Choice Question, Every rational number is, a) Real number, b) Integer, c) Whole number, d) Natural number, , 2., , Decimal representation of a rational, number cant be, a) terminating, b) non-terminating, c) non-terminating repeating, d) non - terminating non - repreating, , 3., , The value of, a) 2, c) 4, , 4., , The value of, a) 2, c) 5, , 5., , 6., , 7., , 16 is, b) 8c, d) 16, 4, , (, , 8− 5, , )(, , ), , 8 + 5 is, , b) 3, d) 1, , b) 4, , 16-1/4 is equal to, a) 2, b) 1/4, Ans. 1. a, 2. d, 3. a, 4. b, 5. a, 6. d, 7. b, 8. c, 9. d, 10. c, , 10., , i., , 3+2, , d) 4, , 5−2, , Ans. Rationalizing factor of, 5 − 2is 5 + 2, 5+2, , =, , is, ii., , b) 3 − 2, 1, c), 3−2, 1, d), 3+2, , c) 1/2, , 5+2, , =, 1, , d) 2, , Rationalise the denominator and simplify., , 5−2, , The rationalising factor of, , c) 8, , Answer the following QUESTIONS, , 8 5 is an, a) a rational number, b) natural number, c) an integer, d) an irrational number, , a) 3 + 2, , 8., , is equal to, , 2, a) 1, , 1., , The product of two rational numbers., a) is always an rational number, b) is always an irrational number, c) may be a rational number, d) may be an irrational number., , 8, , 9., , 5, , 5+2, , ×, , (, , 5+2, , ) (, , 5+2 +2, , ( 5), , 2, , − ( 2), , 5+2, , ), , 2, , 5+ 4 5 + 4, = 9+4 5, 1, , 5+ 2 3, 7+4 3, , Ans. Rationalizing factor of, 7 + 4 3 is 7 − 4 3, 5+ 2 3, , ×, , 7−4 3, , 7+4 3 7−4 3, , Rationalising factor of, a) 3 a, , b) a, , c) 3 a 2, , d) a, , 3, , a is, , =, , (, , ), , (, , 5 7−4 3 +2 3 7−4 3, , (7), , 2, , (, , − 4 3, , ), , ), , 2, , 35 − 20 3 + 14 3 − 8 9, 49 − 16 × 3, 35 − 6 3 − 8 × 3 35 − 6 3 − 24, =, =, 49 − 48, 1, =

Page 14 :
×, 7+4 3 7−4 3, , (, , ), , (, , 5 7−4 3 +2 3 7−4 3, = 1 – Number System, Chapter, 2, 2, 3, Chapter 1 – Number, ( 7 ) − 4 System, , (, , ), , ), , 13, 13, , 35 − 20 3 + 14 3 − 8 9, 49 − 16 × 3, 35 − 6 3 − 8 × 3 35 − 6 3 − 24, =, =, 49 − 48, 1, = 11 − 6 3, , \ Five irrational numbers are 17, 18, 19, , =, , iii., , 4 3+ 2, 3+ 2, , Ans. Rationalizing factor of, 3 + 2 is 3 − 2, 4 3+ 2, 3+ 2, =, , 4 3, , (, , 20 , 21 between 4 and 5, 3., , Prove that, , 2 + 3 is irrational number., Ans. Let us, w assume that, 2 + 3 is an rational number, =, 2 + 3 p where p, q ∈ z q ≠ 0, q, Squaring on both side, 2, , 3− 2, , ×, , 3− 2, , ), , (, ( 3) − ( 2 ), , 3− 2 + 2, 2, , 3− 2, , =, 2, , ), , a− b, , Ans. Rationalizing factor of, a − b is a + b, , =, , ab, , 2, , 2, , 2., , p2 + q 2, q2, q 1,  ×, p 2, , p2 + q 2, is a rational number but, 2pq, , \ 2 + 3 is an irrational number., , 2, , 4., , 2, , Find 5 irrational numbers between 4, and 5., Ans. Square of 4 is 16 and square of 5 is 25., Taking square root numbers between 16, and 25, , 3 +3, , 3 is not a rational number, \ It is contradiction to our assumption, , a+ b, , a b + ab, a−b, a b +b a, =, a−b, =, , \, , a+ b, , ( a + b), ( a) −( b), , q, , =, ,  p2 + q 2, 3=, 2,  q, p2 + q 2, 3=, 2pq, , ab, , a− b, , 2, , 2, , 2 3p, , = 10 − 3 6, , ×, , − 3, , p2, 2 3 p = 2 +3− 2, q q, , = 12 − 2 − 4 6 + 6, , ab, , p, , p2, −2 3 p +3, 2=, q, q2, , 2, , 4 9 −4 6 + 6 − 4, =, 3− 2, = 4×3 − 4 6 + 6 − 2, , iv., , (q ), ( p q ) − 2× p q, , 2), (=, , Ans., , Find the rational number whose decimal, expansion 0.142857........, Let r = 0.142857, r = 0.1428571428.57..... (1), 1000000 r = 142857.142857.... ( 2 ), Subtract eqn ( 2 ) & (1), 1000000r = 142857.142857..., r = 0.142857......, 999999r = 142857.0000, 142857, r=, 999999, r= 1, 7

Page 15 :
Let r = 0.142857, r = 0.1428571428.57..... (1), 1000000 r = 142857.142857.... ( 2 ), 14, 14, Subtract eqn ( 2 ) & (1), , IXIX, Standard, – Mathematics, Standard, – Mathematics, , 1000000r = 142857.142857..., r = 0.142857......, 999999r = 142857.0000, 142857, r=, 999999, r= 1, 7, 5., , Simplify, , (, , )(, , i. 3 + 5 3 − 5, , ), , Ans. It is in the form of, ( a + b )( a − b ) = a 2 − b 2, a 3&, b, =, =, , 5, , (3 + 5 )(3 − 5 ) = (3) − ( 5 ), 2, , 2, , = 9−5, =4, ii., , (, , 5+ 2, , ), , 2, , Ans. It is in the form, 2, ( a + b ) =a 2 + 2ab + b 2, , (, , ) ( 5), 2, , 5+ 2 =, , 2, , +2 5× 2 +, , =, 5 + 2 10 + 2, = 7 + 2 10, , ( 2), , 2

Page 16 :
45, 15, , Chapter - -25, CHAPTER, , Introductionto, toEuclid’s, Euclid’sGeometry, Geometry, Introduction, Key Points :, , ●, ●, ●, ●, ●, ●, ●, , Geometry word is derived from two greek words. Geo means earth and metron means, measurement., Euclid is called father of geometry., Axioms : The general statements which are accepted without question and which are applicable, to all branches of science are commonly called axioms., Postulates : The statements which are particular to geometry and accepted without question, are called potulates., Undefined objects : Certain objects which cannot be defined using the terms already known., Ex : point, line, plane, Axioms (or) postulates are the assumptions which are obvious universal truths, they are not, proved., Theorems are statements which are proved using definitions, axioms , previously proved, statements and deductive reasoning., , Some of Euclid’s axioms, , 1. Things which are equal to the same thing are equal to one another., 2. If equals are added to equals, the wholes are equal., 3. If equals are subtracted from equals, the remainders are equal., 4. Things which coincide with one another are equal to one another., 5. The whole is greater than the part, 6. Things which are double of the same things are equal to one another., 7. Things which are halves of the same things are equal to one another., Some Euclid’s Postulates, , 1. A straight line may be drawn from any one point to any other point., 2. A terminated line can be produced indefinitely., 3. A circle can be drawn with any centre and any radius., 4. All right angles are equal to one another., 5. If a straight line falling on two straight lines makes the interior angles on the same side of it taken, together less than two right angles, then the two straight lines, if produced indefinitely, meet on, that side on which the sum of angles is less than two right angles., 6. The equivalent versions of Euclid’s fifth postulate are, i. ‘For every line l and for every point p not lying on l, there exists a unique line m passing, through p and parallel to 1, ii. Two distinct intersecting lines cannot be parallel to the same line.

Page 17 :
16, 46, , IX, IXStandard, Standard––Mathematics, Mathematics, The other terms that need to be defined, first is angle, adjacent angles, right angle., , 2.1, Exercise 5.1, , 1., , Which of the following statements are, true and which are false? Give reasons, for your answers., , i., , Only one line can pass through a single, point, Ans. False, Infinitely many lines can pass, through a single point, ii., , There are an infinite number of lines, which pass through two distinct points., Ans. False, statement contradicts the postulate I., There is a unique line that passes through, two distinct points., iii., , A terminated line can be produced, indefinitely on both the sides., Ans. True, from postulate II A terminated line, can be produced indefinitely, iv., , If two circles are equal, then their radii, are equal., Ans. True, from Axiom 4 “The things which, coincide with one another are equal to one, another”., v., , In Fig 25.9, if AB = PQ and PQ = XY,, then AB = XY., B, Q, Y, , A, P, X, Ans. True, from Axiom 1 “The things which are, equal to the same thing are equal to one, another”., 2., , Give a definition for each of the following, terms. Are there other terms that need, to be defined first? What are they, and, how might you define them?, , i., Parallel lines, Ans. Parallel lines : Lines which do not intersect, anywhere, each, other are called parallel lines. Other, term involved is the “Plane”., ii. Perpendicular lines, Ans. Perpendicular lines : Two lines which are, at a right angle to each other are called, perpendicular lines., , iii. Line segment, length line., between, points, is called, Ans. The, It is definite, a terminated, Thetwo, other, terms, that, line., otherand, terms, that need is line and point, needThe, is line, point., iv. Radius of a circle, Ans. Radius : It is the distance between centre, to any point on the circumference of a, circle., The other terms that need is “circle, center, and line”., v., Square, Ans. A quadrilateral with all the four sides and, all the four interior angles of measure 90o, each are equal., The other terms that need is equilateral and, right angle., 3., , Consider two ‘postulates’ given below :, i. Given any two distinct points A and B,, there exists a third point C which is in, between A and B., ii. There exist at least three points that, are not on the same line., Do these postulates contain any, undefined terms? Are these postulates, consistent? Do they follow from Euclid’s, postulates ? Explain., Ans. These postulates contain two undefined, terms such as point and line., Yes these postulates are consistent because, they deal with two different situations., i. The given two points A and B, there is a, point C lying on the line in between them., ii. The given A and B we can take C not, lying on the line through A and B. These, ‘postulates’ do not follow from Euclid’s, postulates however, they follow from, Axiom 5.1., 2, 4., , If a point C lies between two points A, and B such that AC = BC, then prove, 1, that AC = AB. .Explain by drawing, 2, the figure.

Page 18 :
17, 47, , Chapter 5, 2 –– Introduction, Introduction to, to Euclid’s, Euclid’s Geometry, Geometry, Chapter, Ans., A, , C, , AB + BC = BC + CD, AB = CD [Axiom (3)], , B, , AC = BC, AC + AC = BC + AC [equals are added to equals], [From Fig AB = AC + BC], 2AC = AB, AB, AC =, 2, 1, AC = AB, 2, , 5., , In Question 4, point C is called a midpoint of line segment AB. Prove that, every line segment has one and only one, mid-point., Ans. Let C and D be the two mid -points of line, segment AB., A, , C, , B, , A, , D, , B, , If C is the mid point of AB from Axiom 4, AC = BC → (i), Similarly, D is the midpoint of AB from, Axiom 2, AD = BD → (ii), We have AB = AB, AC + BC = AD + BD [From (i) & (ii)], AC + AC = AD + AD, 2AC = 2AD, \AC = AD, When we superimpose AD over AC and, BC over, thatthat, D exactly, overlap, BD, overBC, BCwewefind, find, D exactly, over, on, C., It, implied, that, D, and, C, are, not, twotwo, C. It implies that D and C are not, different points. \We can conclude that, mid-point of a line segment is unique., 6., , In fig.5.10,, if AC = BD, then prove that, 2, AB = CD., , C, B, A, Ans. AC = BD Given ....(1), , D, , AC = AB + BC [point B lies on A & C] →(2), BD = BC + CD [point C lies on B & D] →(3), , Substituting Eqn (2) & (3) in eqn (1), , 7., , Why is Axiom 5, in the list of Euclid’s, axioms, considered a ‘universal truth’?, (Note that the question is not about the, fifth postulate)., Ans. Euclid’s Axiom 5 states that “The whole is, greater than the part”, Since this is true for anything in any part, of the world (or) life. So, this a universal, truth., Exercise 2.2, 5.2, , 1., , How would you rewrite Euclid’s fifth, postulate so that it would be easier to, understand?, Ans. Two distinct intersecting lines cannot be, parallel to the same line., Ex :, E, D, , A, , B, , C, 2., , F, , Does Euclid’s fifth postulate imply the, existence of parallel lines? Explain., Ans. If a straight line l falls on two straight, lines m and n such that sum of the interior, angles on one side of l is two right angles,, then by Euclid’s fifth postulate the lines m, and n will not meet on this side of l. Next,, we know that the sum of the interior angles, on the other side of l will also be two right, angles., Therefore, they will not meet on the other, side also. So, the lines m and n never meet, parallel., and therefore, are, therefore, parallel.

Page 19 :
18, 48, , IX, IX Standard, Standard –– Mathematics, Mathematics, Ans., , Additional Problems, , I., , Multiple Choice Questions, , 1., , Who is the father of geometry, a) Eucld, b) Ramanujan, c) Pythogoras, d) Thales, , 2., , If a = 30 and b = a then b = 30 by, a) Axiom 2, b) Axion 1, c) Axiom 3, d) Axiom 4, , How many straight lines can be drawn, through a point, a) one, b) two, c) infinity, d) 0, Ans. 1) a, 2) b, 3) c, , A 3 cm, , P 4 cm, 7 cm, From the above figure, AB > AP and AB > BP, 4., Ans., , Write one example “Halves of equals, are equal”, A, , 3., , II., , 1., Ans., , Answer the following questions, , Give one example for axiom “things, which are equal to the same thing are, equal to one another”, A, C, P, , 5 cm, 5 cm, , 5 cm, AB = CD = 5 cm ...(1), AB = PQ = 5 cm ....(2), From eqn (1) & (2), CD = PQ, 2., Ans., , B, D, Q, , Write one example for “If equals are, added to equals, the wholes are equal”., A 4 cm, C 4 cm, , 3 cm, , E, , F, 3 cm, AB = CD = 4 cm and BE = DF = 3 cm, AE = AB + BE = 4 + 3 = 7 cm ...(1), CF = CD + DF = 4 + 3 = 7 cm ...(2), From (1) & (2), AE = CF, 3., , Write one example “the whole is greater, than its parts”, , E, B, , D, 30, o, 60o 30, o, , B, CBD = 1 ABC, 2, CBD = 30o, ... (1), ABD = 1 ABC, 2, ABD = 30o, .... ( 2 ), From (1) & ( 2 ), ABD = CBD, , C

Page 20 :
49, 19, , Chapter, CHAPTER -- 36, , Lines and Angles, Key Points :, , ●, ●, ●, ●, ●, ●, ●, ●, ●, ●, ●, ●, ●, ●, ●, ●, ●, ●, ●, ●, , ●, ●, , Line - Segment : A line with two end points is called line - segment., A part of a line with one end point is called a ray., Collinear points : If three or more points lie on the same line., Non - collinear points : If three (or) more points not lie on the same line., Angle : Measurement at intersection of two rays at the common end point., Numerical measurement called degree., Geometrical instrument used to measure degree is called protractor., Acute angle : Angle measures between 0o and 90o., Right angle : Measurement of an angle is exactly equal to 90o., Obtuse angle : Measure of an angle is greater than 90o and less than 180o., Straight angle : Measurement of an angle is equal to 1800., Reflex angle : Measurement of an angle is greater than 180o and less than 360o., Complementary angle : Sum of the measure of two angles is 90o., Supplementary angles : Sum of the measure of two angles is 180o., Adjacent angles : A pair of angles made by a ray standing on a line., Vertically opposite angles : When two straight lines intersect each other a pair of angles which, do not form a linear pair., Alternate angles : When a transversal cuts a pair of lines, the angles formed by the transversal, which is not a linear pair and lying on both sides of the transversal., Corresponding angles : When a transversal cuts a pair of lines. The angles formed by the, transversal which lie on the same side of the transversal and also on the similar side of the two, lines., If a ray stands on a line, then the sum of two adjacent angles so formed is 180o . This property, is called as the linear pair., If a transversal intersects two parallel lines then, i. Each pair of corresponding angles is equal, ii. Each pair of alternate interior angles is equal., iii. Each pair of interior angles on the same side of the transversal is supplementary., If a transversal intersects two lines such that either, i. Any one pair of corresponding angles is equal or, ii. Any pone pair of alternate interior angles on the same side of the transversal is supplementary, then the lines are parallel., Lines which are parallel to a given line are parallel to each other., The sum of the three angles of a triangle is 180o.

Page 30 :
29, , CHAPTER - 4, , Polynomials, Key Points :, , Algebraic expressions : An algebraic expression is the combination of constants ans variables, connected by the four fundamental operations eg : (+, –, × , ÷), Types of algebraic expression, , ●●, ●●, ●●, ●●, , Monomial : An algebraic expression contains only one term., Ex : 2x , 3x2 , –5x e+c, Binomial : An algebraic expression containing two terms., Ex : 3x + 2, 5a2 + 9 etc, Trinomial : An algebraic expression containing three terms., Eg : x2 + 3x + 2, 5m2 + 9m - 10 etc..., Polynomial : An algebraic expression of the form, P(x) = a0 + a1x + a2x2 + a3 x3 + .... +anxn in, which the variables involved have only non-negative integral exponents is called a polynomial, in x., Degree of a polynomial : The highest exponent of the variable in a polynomial is called degree., , Types of polynomials based on degree., , ●●, ●●, ●●, ●●, ●●, ●●, ●●, ●●, , Constant polynomials : Height degree of variable is zero general form is axo = a, Linear polynomial : The highest degree of the variable is one., General form is ax + b where a ≠ 0, Ex : 2x + 3, 3a + 8, m - 8, etc, Quadratic polynomial : The highest degree of the variable is two, General form is ax2 + bx + c where a ≠ 0, Ex : x2 + 3x + 5 , y2 - 5y + 8 etc., Cubic polynomial : The highest degree of the variable is three, General form is ax3 + bx2 + cx + d where a ≠ 0, Ex : x3 + 3x2 + 5x + 8, Zero of the polynomial : P(x) is a polynomial and k is any real number such that P(k) then k, is called a zero of the polynomial P(x)., Linear polynomial has one zero., Quadratic polynomial has two zeroes., Cubic polynomial has three zeroes., Similarly polynomial of degree ‘n’ has ‘n’ zeroes.

Page 31 :
30, ●●, ●●, ●●, ●●, ●●, , IX Standard – Mathematics, , Remainder theorem : If a polynomial P(x) is divided by a liner polynomial (x - a), then the, remainder is P(a)., Remainder theorem holds good only when the divisor is a binomial and in the linear form, (x - a), Factor theorem : If P(a) = 0, then (x - a) is a factor of P(x). When (x-a) is a factor of P(x),, then P(a) = 0., If the remainder is equal to zero, both the divisor and quotient are factors of the dividend., If P(a) is zero, that means the (x - a) must be a factor of polynomial P(x) remainder is zero., , Algebraic Identities, , ( i )( x + a )( x + b ) = x 2 + ( a + b ) x + ab, 2, ( ii )( a + b ) =a 2 + 2ab + b 2, 2, ( iii )( a − b ) =a 2 − 2ab + b 2, ( iv ) ( a 2 − b 2 ) =( a + b )( a − b ), ( v )( x + a )( x + b )( x + c ) = x 3 + ( a + b + c ) x 2 + ( ab + bc + ca ) x + abc, 3, ( vi )( a + b ) =a 3 + 3a 2 b + 3ab 2 + b3 ( or ) a 3 + b3 + 3ab ( a + b ), 3, ( vii )( a − b ) = a 3 − 3a 2 b + 3ab 2 − b3 ( or ) a 3 − b3 + 3ab ( a − b ), ( viii ) a 3 + b3 = ( a + b ) ( a 2 − ab + b 2 ), ( ix ) a 3 − b3 = ( a − b ) ( a 2 + ab + b 2 ), ( x )( a + b + c ) = a 2 + b 2 + c2 + 2ab + 2bc + 2ca, ( xi ) a 3 + b3 + c3 − 3abc = ( a + b + c ) ( a 2 + b 2 + c2 − ab − ac − ca ), ( xii ) a 4 + a 2 b 2 + b 4 = ( a 2 + ab + b 2 )( a 2 − ab + b 2 ), 2, , ( xiii )( a + b + c ), , 3, , − a 3 − b3 − c3= 3 ( a + b )( b + c )( c + a )

Page 32 :
31, , Chapter 4 – Polynomials, Exercise 4.1, , 1., , Which of the following expressions are, polynomials in one variable and which, are not? State reasons for year answer., , i., 4x2 - 3x + 7, Ans. 4x2 - 3x + 7 yes, is a polynomial in one, variable and degree of the variable is, whole number., ii., , iii., , 3 t +t 2, Ans. No, It is a polynomial in one variable and, degree of the variable is not whole number., 2, y+, y, , Ans. No, It is a polynomial in one variable, and degree of the variable is not a whole, number., v., x +y +t, Ans. No, It is a polynomial in three variables and, degree of the variables is whole number., 10, , 2., , 3, , 50, , Write the coefficients of x in each of the, following :, 2, , i., 2 + x2 + x, Ans. Coefficient of x2 in 2 + x2 + x is 1., ii. 2 – x2 + x3, Ans. Coefficient of x2 in 2 – x2 + x3 is –1., p 2, x +x, 2, Ans. Coefficient of x2 in p/2 x2 + x3 is p/2., iii., , iv., , 2x − 1, , Ans. Coefficient of x2 in 0x2 +, 3., , 4., , 2x − 1 is 0., , Give one example each of a binomial of, degree 35, and of a monomial of degree, 100., , Write the degree of each of the following, polynomials :, , i., 5x3 + 4x2 + 7x, Ans. Degree of 5x3 + 4x2 + 7x is 3., ii. 4 – y2, Ans. Degree of 4 – y2 is 2., iii., , y2 + 2, , Ans. yes, It is a polynomial in one variable and, degree of the variable is whole number., , iv., , Ans. Binomial of degree 35 is m35 – 3 and, monomial of degree 100 is 3y100., , 5t − 7, , Ans. Degree of 5t − 7, , is 1., , iv. 3, Ans. Degree of 3 (or) 3x0 is 0. Degree of, constant polynomial is zero., 5., , Classify the following as linear,, quadratic and cubic polynomials :, , i., x2 + x, Ans. Degree of x2 + x is 2 \It is quadratic, polynomial., ii. x – x3, Ans. Degree of x – x3 is 3 \It is a cubic, polynomial., iii. y + y2 + 4, Ans. Degree of y + y2 + 4 is 2.\It is a quadratic, polynomial., iv. 1 + x, Ans. Degree of 1 + x is, polynomial., , \It is a linear, , v., 3t, Ans. Degree of 3t is 1. \It is a linear polynomial., vi. r2, Ans. Degree of r2 is 2. \It is a quadratic, polynomial., vii. 7x3, Ans. Degree 7x3 is 3. \It is cubic polynomial., Exercise 4.2, , 1., , Find the value of the polynomial 5x – 4x2, + 3 at, Ans. 5x – 4x2 + 3

Page 33 :
32, i., x=0, Ans. P(0) = 5(0) – 4(0)2 + 3, = 0 – 0 + 3 = 3, P(0) = 3, ii. x = –1, Ans. P(–1) = 5(–1) –4(–1)2 + 3, = –5 – 4 + 3 = –9 + 3, = –6, , IX Standard – Mathematics, p(2) = (2)2 – 1 = 4 – 1, p(2) = 3, 3., i., Ans., , ii. p(t) = 2 + t + 2t2 – t3, Ans. p(0) = 2 + (0) + 2(0)2 – (0)3 = 2 + 0 + 0 – 0, p(0) = 2, p(1) = 2 + (1) + 2(1)2 – (1)3 = 2 + 1 + 2 – 1, p(1) = 4, and p(2) = 2 + (2) + 2(2)2 – (2)3 = 2 + 2 +, 8–8, p(2) = 4, iii. p(x) = x3, Ans. p(0) = (0)3, p(0) = 0, p(1) = (1)3, p(1) = 1, p(2) = (2)3, p(2) = 8, iv. p(x) = (x – 1) (x + 1), Ans. p(x) = x2 – 1 [(a + b) (a – b) = a2 – b2], p(0) = (0)2 – 1 = –1, p(0) = –1, p(1) = (1)2 – 1 = 1 – 1, p(1) = 0, , ( g3 ) =, (, , p −1, , 3× − 1 +1, 3, , =−1 + 1 =0, , 3, , 0, )=, , \ − 1 is the zero of the polynomial p ( x ), 3, , Find p(0), p(1) and p(2) for each of the, following polynomials :, , i., p(y) = y2 – y + 1, Ans. P(0) = (0)2 – (0) + 1 = 0 – 0 + 1, P(0) = 1, p(1) = (1)2 – (1) + 1 = 1 – 1 + 1, p(1) = 1, and p(2) = (2)2 – (2) + 1 = 4 – 2 + 1 = 5 – 2, p(2) = 3, , 1, p ( x ) =+, 3x 1, x =, −, 3, p − 1, , iii. x = 2, Ans. P(2) = 5(2) – 4(2)2 + 3, =10 – 4 x 4 + 3, = 10 – 16 + 3 = 13 – 16 = –3, P(2) = –3, 2., , Verify whether the following are zeros of, the polynomial, indicated against them., , ii., Ans., , p ( x=, x, ) 5x − p, =, , ( 5) =, p ( 4 )=, 5, p 4, , 4, 5, , 5× 4 − p, 5, 4−p ≠ 0, , \ 4 is not a zero of the polynomial p ( x ), 5, iii. p(x) = x2 – 1 , x = 1, –1, Ans. x = 1 p(1) = (1)2 – 1 = 1 – 1, p(1) = 0, x = –1 p(–1) = (–1)2 – 1 = 1 – 1, p(–1) = 0, \1 and –1 are the zero’s of the polynomial, p(x)., iv. p(x) = (x + 1) (x – 2), x = –1,2, Ans. x = –1, p(–1) = (–1+1) (–1–2), p(–1) = 0 x –3 = 0, p(–1) = 0, x = 2 p(2) = (2 + 2) (2 – 2), , =4x0=0, p(2) = 0, –1 and 2 are the zeros of polynomial p(x), v., p(x) = x2 , x = 0, Ans. x = p(0) = (0)2 = 0, p(0) = 0, 0 is the zero of polynomial p(x)

Page 34 :
33, , Chapter 4 – Polynomials, vi., Ans., , vii., , 4., , m, p(x) =, −, llx + m, x =, l, −m,  m, +m, p−  =, l×, l,  l ,  m, p−  =, 0,  l , m, \ − is the zero of the polynomial p ( x ), l, , 1 2, p(x) =, 3x 2 − 1, x =, −, ,, 3 3, , Ans., , 2, , −1, x = p  − 1  =, 3  − 1  − 1, 3, 3, , 3 , 3 1 −1, =×, 3, , p  − 1  = 1 − 1 = 0, 3, , p  − 1  =, 0, 3, , 2, ,  2 ,  2 , p, =,  3,  −1, 3  3,  2, 4, =3 × − 1, 3,  2 , p,  = 4 −1 = 3,  3, 1, 2, \−, is a zero of p ( x ) but, is not a, 3, 3, zero of p ( x ), , x, =, , 2, , viii. p ( x ) = 2x + 1, x =, Ans., , ( ), , 1, 2, , x = 1 p 1 = 2× 1 +1 = 1+1, 2, 2, 2, 1, p, =2, 2, \ 1 is not a zero of p ( x ), 2, , ( ), , Find the zero of the polynomial in each, of the following cases :, , i., p(x) = x + 5, Ans. p(x) = x + 5, p(x) = 0, x+5=0, x = –5, \–5 is the zero of the polynomial p(x), ii. p(x) = x – 5, Ans. p(x) = x – 5 p(x) = 0, x–5=0, x=5, \5 is the zero of the polynomial p(x), iii. p(x) = 2x + 5, Ans. p(x) = 2x + 5 p(x) = 0, 2x + 5 = 0, 2x = –5, x = –5/2, \–5/2 is the zero of the polynomial p(x), iv. p(x) = 3x – 2, Ans. p(x) = 3x – 2, p(x) = 0, 3x – 2 = 0, 3x = 2, x = 2/3, \2/3 is the zero of the polynomial p(x), v., p(x) = 3x, Ans. p(x) = 3x p(x) = 0, 3x = 0, x = 0/3 = 0, \0 is the zero of the polynomial p(x), vi. p(x) = ax , a ≠ 0, Ans. p(x) = ax, a ≠ 0, ax = 0, x = 0/a = 0, \0 is the zero of the polynomial p(x), vii. p(x) = cx + d, c ≠ 0,c,d are real numbers., Ans. cx + d = 0, cx = –d, x = –d/c, \-d/c is the zero of the polynomial p(x)

Page 35 :
34, , IX Standard – Mathematics, Ans., , Exercise 4.3, , 1., , Find the remainder when x3 + 3x2 + 3x +, 1 is divided by, , (, , p −5, , i., x +1, Ans. x + 1 = 0 => x = –1, 2, 3, 2 23, p ( −1) =(p−(1−)1)+=, 3( 1−)1)++3 3( −(1) ++13 ( −1) + 1, , Ans., , 1, 2, , x − 1 ⇒ x –= 1 = 0 ⇒ x = 1, 2, 2, 2, , ( 2 ) = ( 12 ) + 3( 12 ), 3, , p 1, , 2, , ( 2) +1, , +3 1, , = 1 + 3× 1 + 3 +1, 8, 4, 2, = 1 +3 +3 +1, 8, 4, 2, 1, LCM of 1, 2, 4 &8is8, 1 6 12 8, = + + +, 8 8 8 8, 27, Remainder =, 8, iii. x, Ans. x => x = 0, 3, 2, p (0) = (0) + 3(0) + 3(0) + 1, , 2., , Find the remainder when x3 – ax2 + 6x – a, is divided by x – a., Ans. p(x) = x3 – ax2 + 6x –a, x − a ⇒ x −=, a 0 =, x a, p (a ) =(a ) − a (a ) + 6 (a ) − a, 3, , 2, , p ( a ) = a 3 − a 3 + 6a − a, , p (a ) = 0, , p ( a ) = 5a, Remainder = 5a, 3., , Check whether 7 + 3x is a factor of 3x3 +, 7x., Ans. 7 + 3x is a factor of 3x3 + 7x. If 3x3 + 7x is, divisible by 7 + 3x by leaving remainder is, zero., p (=, x ) 3x 3 + 7x, , p (0) = 1, , 7 + 3x ⇒ 3x + 7 =0 ⇒ 3x =−7, ⇒x=, −7, 3, , Remainder =1, , p −7, , = 0 + 0 + 0 +1, , (, , iv. x + p, Ans., x + p ⇒ x + p = 0, x =− p, p ( −p ) =, , ( −p ), , 3, , + 3 ( −p ) + 3 ( −p ) + 1, 2, , p ( −p ) = −p3 + 3p2 − 3p + 1, Remainder = − p3 + 3p2 − 3p + 1, v., , 2, , −125 75 15, + − +1, 8, 4 2, −125 150 60 8, =, +, − +, 8, 8, 8 8, 185 158 −27, =, −, +, =, 8, 8, 8, −27, Remainder =, 8, , =, 1) 0Remainder, =, Remainder, 0, =, p ( −1) 0p ( −=, 0, x−, , 2, , 5 + 2x, , 2, , ) =( − 5 2 ) + 3 ( − 5 2 ) + 3 ( −5 2 ) + 1, 3, , =, , =−1 + 3 −=−, 3 +11+ 3 − 3 + 1, , ii., , 5 + 2x ⇒ 5 + 2x =0 2x =−5 ⇒ x =− 5, , ) (, , ), , 3, , (, , ), , = 3 −7, +7 −7, 3, 3, 3, −343 49, 3×, =, −, 27, 3, −343 49, =, −, 9, 3, −343 147, =, −, 9, 9, −490, =, ≠0, 9, Since remainder not equal, zero, Since, equal+to0 zero., 3 3 + 7x, \7, +, 3x, is, not, a, factor, of, 3x, \ 7 + 3x is not a factor of 3x + 7x

Page 36 :
35, , Chapter 4 – Polynomials, 2., , Exercise 4.4, , 1., , Determine which of the following, polynomials has (x + 1) a factor :, , i., x3 + x2 + x + 1, Ans. p(x) = x3 + x2 + x + 1, x + 1 ⇒ x + 1 =0 x =− 1, , ( ii ) p ( x ) =x 3 + 3x 2 + 3x + 1, g ( x ) =x + 2, ( iii ) p ( x ) = x 3 − 4x 2 + x + 6, g ( x ) = x − 3, Ans., , p ( −1) = ( −1) + ( −1) + ( −1) + 1, 3, , 2, , =−1 + 1 − 1 + 1, p ( −1) =, 0, By factor theorem x + 1is a factor of, , p ( −1) =, 0, , ii. x4 + x3 + x2 + x + 1, Ans. p(x) = x4 + x3 + x2 + x + 1, x + 1 ⇒ x + 1 =0 ⇒ x =−1, , By factor theorem g ( x ) is a factor of p ( x ), , ( ii ) p ( x ) =x 3 + 2x 2 + 3x + 1, g ( x ) =x + 2, , p ( −1) = ( −1) + ( −1) + ( −1) + ( −1) + 1, 3, , 2, , x + 2 =0 ⇒ x =−2, , = 1−1+1−1+1, , p ( −2 ) =( −2 ) + 3 ( −2 ) + 3 ( −2 ) + 1, 3, , p ( −1) =1 ≠ 0, , p ( −2 ) =1 ≠ 0, , x 4 + x3 + x 2 + x + 1, , \ By factor theorem g ( x ) is a factor of p ( x ), , iii. x4 + 3x3 + 3x2 + x + 1, Ans. p(x) = x4 + 3x3 + 3x2 + x + 1, x + 1 ⇒ x + 1 =0 ⇒ x =−1, , ( iii ) p ( x ) = x 3 − 4x 2 + x + 6, g ( x ) = x − 3, x −3 = 0 ⇒ x = 3, p ( 3=, ), , p ( −1) =( −1) + 3 ( −1) + 3 ( −1) + ( −1) + 1, 3, , 2, , p ( −1) =1 ≠ 0, , Ans., , − 4 ( 3) + 3 + 6, 2, , p ( 3) = 0, \ By factor theorem g ( x ) is a factor of p ( x ), , 2, , x + 3x + 3x + x + 1, iv., , 3, , p ( 3) = 36 − 36 = 0, , By factor theorem x + 1is not factor of, 3, , ( 3), , p ( 3) = 27 − 36 + 3 + 6, , = 1− 3 + 3 −1+1, , 4, , 2, , =−8 + 12 − 6 + 1, , By factor theorem x + 1is not factor of, , 4, , ( i ) p ( x ) = 2x 3 + x 2 − 2x − 1, g ( x ) =x + 1 ⇒ x + 1 =0 ⇒ x =−1, 3, 2, p ( −1) = 2 ( −1) + ( −1) − 2 ( −1) − 1, =−2 + 1 + 2 − 1, , x3 + x 2 + x + 1, , 4, , Use the factor theorem to determine, whether g(x) is a factor of p(x) in each of, the following cases :, ( i ) p ( x ) =2x 3 + x 2 − 2x − 1, g ( x ) =x + 1, , (, , ), , x3 − x 2 − 2 + 2 x + 2, , 3., , x + 1 ⇒ x + 1 =0 ⇒ x =−1, , i., p(x) = x2 + x + k, Ans. x – 1 => x – 1 = 0 => x = 1, 2, p (1) = (1) + (1) + k, p (1) = 0, , (, , ), , p ( −1) = ( −1) − ( −1) − 2 + 2 ( −1) + 2, 3, , 2, , =−1 − 1 + 2 + 2 + 2, p ( −1) =, 2 2, By factor theorem x + 1is not factor of, , (, , ), , x3 − x 2 − 2 + 2 x + 2, , Find the value of k, if x – 1 is a factor of, p(x) in each of the following cases :, , 0= 2 + k, k= −2

Page 38 :
37, , Chapter 4 – Polynomials, 2., , Exercise 4.5, , 1., , Use suitable identities to find the, following products :, i., (x + 4) (x + 10), Ans. Using the identity, ( x + a )( x + b ) = x 2 + ( a + b ) x + ab, , ( x + 4 )( x + 10 ) =, , i., 103 x 107, Ans. (100 + 3)(100 + 7), Using identity, , ( x + a )( x + b ) =, , x 2 + ( 4 + 10 ) x + 4 × 10, , =, , x 2 + ( 8 − 10 ) x + 8 × −10, , = x 2 + ( −2 ) x − 80, , = 8100 + 990 + 30, = 9120, , x = 3x, a = 4 & b = − 5, , iii. 104 x 96, Ans. (100+4)(100 – 4), Using the identity, ( a + b )( a − b ) = a 2 − b 2, , ( 3x + 4 )( 3x − 5) =, ( 3x ), + ( 4 − 5 ) 3x + 4 × −5, = 9x 2 + ( −1) 3x − 2x, 0, 2, , =, =, a 100, &b 4, , = 9x 2 − 3x − 20, , 4 ) (100 ) − ( 4 ), (100 + 4 )(100 − =, 2, ,  2 3  2 3 ,  y +  y − , 2 , 2, , Ans. Using the identity, ( a + b )( a − b ) = a 2 − b 2, iv., , (y, , 2, , +3, , 2, , )( y, , 2, , −3, , 2, , + ( 3 + 7 )100 + 3 × 7, , ( x + a )( x + b ) = x 2 + ( a + b ) x + ab, 2, 95 × =, 96 ( 90 ) + ( 5 + 6 ) 90 + 5 × 6, , iii. (3x + 4)(3x – 5), Ans. Using the identity, ( x + a )( x + b ) = x 2 + ( a + b ) x + ab, , 2, , 2, , ii. 95 x 96, Ans. (90 + 5)(90 + 6), Using the identity, , = x 2 − 2x − 80, , 2, a y=, &b 3, =, , (100 ), , = 10000 + 10 × 100 + 21, = 10000 + 1000 + 21, = 11021, , ii. (x + 8)(x – 10), Ans. Using the identity, ( x + a )( xx + b ) = x 2 + ( a + b ) x + ab, xa = x , a = 8& b = − 10, , x 2 + ( a + b ) x + ab, , =, x 100,, =, a 3&, =, b 7, , =x 2 + 14x + 40, , ( x + 8)( x − 10=), , Evaluate the following products without, multiplying directly :, , 2, , = 10000 − 16, = 9984, 3., , ) = (y ) − ( 32), 2 2, , = y4 − 9, , 4, , 9x 2 + 6xy + y 2 = ( 3x + y ), , = 9 − 4x 2, , 2, , =, ( 3x + y )( 3x + y ), , =, a 3&, =, b 2x, 2, , i., 9x2 + 6xy + y2, Ans. 9x2 + 6xy + y2, Using the identity, 2, a 2 + 2ab + b 2 = ( a + b ), =, a 3x, =, &b y, , v., (3 – 2x)(3 + 2x), Ans. Using the identity, ( a + b )( a − b ) = a 2 − b 2, , ( 3 − 2x )( 3 + 2x ) = ( 3) − ( 2x ), , 2, , Factorise the following using appropriate, identities :, , 2

Page 43 :
42, , IX Standard – Mathematics, , Ans. W.k.t a+b+c = 0, a 3 + b 3 + c3 =, 3abc, a=, −12, b =, 7&c=, 5, , ( −12 ) + ( 7 ) + ( 5), 3, , 3, , 3, , = 3 × ( −12 )( 7 )( 5 ), , = −1260, ii. (28)3 +(–15)3 +(–13)3, Ans. W.k.t a + b + c =0, a 3 + b 3 + c3 =, 3abc, a=, 28, b =, −15 & c =, − 13, , ( 28) + ( −15) + ( −13), =, 3 × ( 28 )( −15 )( −13), 3, , 3, , , = 4k(3y2 + 2y – 5), , = 4k(3y2 + 5y – 3y – 5), , = 4k[y(3y + 5) –1(3y + 5)], , =4k (3y + 5)(y – 1), Dimensions of cuboid are 4k, (3y + 5), and (y – 1), , 3, , Additional Problems, , I., , Multiple Choice Questions, , 1., , The degree of a quadratic polynomial is, a) 0, b) 2, c) 1, d) 3, , 2., , The degree of the polynomial x2 + 3x3 +, 8 is, a) 2, b) 0, c) 1, d) 3, , 3., , The zeros of the polynomial y2(y + 1) is, a) 0,0,-1, b) 0,0,1 c) 0,1 d) 0,1,1, , 4., , One factor of p3 +8 is, a) (p - 2) b) p2 - 2p + 4, c) p2 + 4, d) p2 + 4p + 4, , = 16380, , 15., i., Ans., , Give possible expressions for the length, and breadth of each of the following, rectangles, in which their areas are given:, Area : 25a2 – 35a + 12, , ( Length ) × ( Breadth ) = 25a 2 − 15a − 20a + 12, = 5a ( 5a − 3) − 4 ( 5a − 3), 5., =, ( 5a − 3)( 5a − 4 ), If length =, ( 5a − 3) then breadth =, ( 5a − 4 )( or ), 6., If length =, ( 5a − 4 ) then breadth =, ( 5a − 3), , ii. Area : 35y2 + 13y – 12, Ans., Length × breadth = 35y 2 + 28y − 15y − 12, , 7., , = 7y ( 5y + 4 ) − 3 ( 5y + 4 ), , ii. 12ky2 + 8ky – 20k, Ans. Length x breadth x height, , x + 1 is a factor of the polynomial, a) x 4 + x 3 + x 2 + 1, c) x 3 + x 2 − x + 1, , l = (5y + 4) & b = (7y – 3) (or), l = (5y + 4) & b = (7y – 3), What are the possible expressions for, the dimensions of the cuboids whose, volumes are given below ?, i., Volume : 3x2 – 12x, Ans. Volume of cuboid = 3x2 – 12x, length x breadth x height = 3x(x – 4), Dimensions of cuboid are 3,x and x - 4, , If x+1 is a factor of the polynomial, 2x2 + kx then the value of k is, a)4 , b) –2, c) –3, d) 2, , b) x 3 + x 2 − x + 1, , =, ( 5y + 4 )( 7y − 3), , 16., , The value of the polynomial 5x - 4x2 + 3, when x = –1 is, a) -6, b) 6, c) 2, d) –2, , d) x 4 + 3x 3 + 2x 2 + x + 1, 8., , The co-efficient of x2 in the expansion of, (x+3)3 is, a) 1, b) 9, c) 27, d) 86, , 9., , The factors of 4x2 + 8x + 3 is, a) (2x + 1)(2x + 3), b) (2x + 2) (2x + 5), c) (x + 1)(x + 3), d) (2x – 1) (2x – 3), , 10., , The remainder when f(x) = 2x3 + 5x2 – 3x, – 2 is divided by g(x) = x – 1

Page 44 :
43, , Chapter 4 – Polynomials, a) 2, 11., , b) –2, , c) –1, , d) 1, , Using identity, a 2 − b 2 = ( a + b )( a − b ), , For what value of a is the polynomial x3, –3x2 + ax – 6 divisible by x – 3?, a) 4, b) –2, c)3, d)2, , The coefficient of x3 in the polynomial, x3+x2 – 4x +7 is, a) –1, b) 7, c) 1, d) –4, Ans. 1. b, 2. d, 3. a, 4. b, 5. a, 6. d, 7. c, 8. b, 9. a, 10. a, 11. d, 12. c, , a 4 − 16b 4 = ( a 2 ) − ( 4b 2 ), 2, , 12., , Answer the following questions, , =, ( a 2 + 4b2 )( a 2 ) − ( 2b ), , 2, , 4., If x + 1/x = 11. Find x2 + 1/x2, Ans. x+1/x = 11, Squaring both sides, 2, x+ 1 2 =, (11), x, x2 + 1 2 + 2 =, 121, x, x2 + 1 2 =, 119, x, , ), , (, , 5., x2 + 1/x2 = 4 find x4 + 1/x4, Ans. x2 + 1/x2 = 4, Squaring both sides, , (x, , 2, , +1, , (x, , a 2 + b 2 − 2ab =, 0, , 2, , +1, , (x ), , 2 2, , =, 0, , x4 + 1, , a=b, , x4 + 1, , 2., Factorise a – b, Ans. a8 – b8, Using the identity a 2 − b 2 = ( a + b )( a − b ), 8, , ( a ) − ( b ) =( a + b )( a − b ), =, ( a + b )( a ) − ( b ), =, ( a + b )( a + b )( a − b ), =( a + b )( a + b ) ( a + b )( a − b ), 4 2, , 4 2, , 4, , 4, , 4, , 2 2, , 4, , 4, , 2, , 2, , 4, , 4, , 2, , 2, , 4, , 4, , 2 2, , 3., Factorize a4 – 16b4, Ans. a4 – 16b4, , 2, , 2, , 2, , =, ( 4), 2, , 4, , 6., , x ), , 2, , =, ( 4), 2, , 2, , + 2 × x2 × 1, , a−b =, 0, 8, , x ), 2, , Squaring both sides, , 2a 2 + 2b 2 − a 2 − b 2 − 2ab =, 0, 2, , 2, , =, ( a 2 + 4b2 ) ( a + 2b )( a − 2b ), , 1., Show that 2(a2 + b2) = (a + b)2, Ans. 2(a2 + b2) = (a + b)2, 2a 2 + 2b 2 =a 2 + 2ab + b 2, , (a − b), , =, ( a 2 + 4b2 )( a 2 ) − ( 2b ), , 2, , x4, x4, , x, , 2, , ( x), , × 1, , 2, , 2, , =, 16, , +2=, 16, = 16 − 2 = 14, , Simplify., 1.5 × 1.5 × 1.5 − 0.5 × 0.5 × 0.5, 1.5 × 1.5 + 1.5 × 0.5 + 0.5 × 0.5, , Ans., =, , 1.5 × 1.5 × 1.5 − 0.5 × 0.5 × 0.5, 1.5 × 1.5 + 1.5 × 0.5 + 0.5 × 0.5, , (1.5) − ( 0.5), 2, 2, (1.5) + 1.5 × 0.5 × ( 0.5), = a 3 − b3 = ( a − b ) ( a 2 + b 2 + ab ) , 3, , 3, , =, , =, , (1.5 − 0.5) (1.5), , =1, , 2, + 1.5 × 0.5 + ( 0.5 ) , , (1.5 )2 + 1.5 × 0.5 + ( 0.5 )2 , , , 2

Page 46 :
59, 45, , Chapter - 7, CHAPTER - 5, , Triangles, Triangles, Key Points :, , ●, ●, ●, ●, ●, ●, ●, , ●, , ●, ●, , ●, ●, ●, ●, ●, ●, ●, ●, ●, ●, , Triangle : A plane figure bounded by three non concurrent line segment in plane is called a, triangle., Triangles are classified according to their angles and their sides., The sum of three interior angles of a triangle is 180o ., An exterior angle of a triangle is the sum of two interior opposite angles., Congruent : Geometrical figures have same shape and size., Congruency of Triangles :- If all the sides and angles of one triangle are equal to the, corresponding sides and angles of the other triangle., Side angle side congruency rule (SAS):- If the two sides and included angle of one triangle are, equal to the corresponding two sides and the included angle of the other triangle, then the two, triangles are congruent., Angle side angle congruency rule (ASA):- If two angles and the common side of one triangle, are equal to the corresponding two angles and the common side of the other triangles then two, triangles are congruent., Side - side - side congruent rule (SSS):- If three sides of one triangle are equal to the three, corresponding sides of the other triangles, then the triangles are congruent., Right angle hypotenuse side congruent rule (RHS) : Two right angled triangles are congruent, if the hypotenuse and a side of one triangle are equal to the hypotenuse and the corresponding, side of the other triangle., Two circle of the same radii are congruent, Two triangles of the same sides are congruent., If two angles and one side of one triangle are equal to two angles and the corresponding sides, of the other triangle then the two triangles are congruent, Angles opposite to equal sides of a triangle are equal., Sides opposite to equal angles of a triangle are equal., Each angle of an equilateral triangle is of 60o., In a triangle angle opposite to the longer side is larger., In a triangle, side opposite to the larger angle is longer., Sum of any two sides of a triangle is greater than the third side., C.P.C.T : Corresponding parts of congruent triangle.

Page 50 :
63, 49, , Chapter, Chapter 75 –– Triangles, Triangles, 4., , A, , B, , C, , D, , Ans. Given : In DABC, AD is the perpendicular, bisector of BC., To prove : DABC is an isosoeles triangle in, which AB = AC, Proof : In DADB and DADC,  AD perpendicular , ADB, = ADC, = 90o , ,  bisector of BC , BD = CD, , [Common side], \ DABD ≅ DADC [SAScongruency ], AC, \ AB =, [CPCT ], AD = AD, , \ ABCis an isosceles D, 3., , ABC is a triangle in which altitudes BE, and CF to sides AC and AB are equal., Show that, (i) ∆ABE ≅ ∆ACF, (ii) AB = AC, i.e., ABC is an isosceles, triangle., A, F, , C, B, Ans. Given : In DABC BE and CF are drawn to, sides AC and AB. BE = CF, To prove :, i. DABC ≅ DACF, ii.AB = AC [ ABCis an isosceles D ], Proof :Consider DABE and DACF, BE = CF [ Given ], , le, ,  BE & CF altitudes , AFC, = 90o , ,  to AB& AC, , EAB = FAC [ Common angle ], , ABC is an isosceles triangle in which, altitudes BE and CF are drawn to equal, sides AC and AB respectively. Show that, these altitudes are equal., A, , AEB, =, , \ DABE ≅ DACF [ ASA congruent ], AC, \ AB =, , F, , E, , C, B, Ans. Given : ABC is an isosceles triangle in, which altitudes BE and CF drawn to AC, and AB. AB = AC, To prove : BE = CF, Proof : In DABE and DACF, AB = AC [Given],  BE & BF altitudes , AEB, = AFC, = 90o , ,  to AC and AB , EAB = FAC [ Common angle ], , DABE ≅ DACF [ ASA congruency ], \ BE =, CF [ C.P.C.T ], , E, , 5., , [C.P.C.T ], , ABC and DBC are two isosceles triangles, on the same base BC. Show that ABD =, ACD., A, , B, , C, , D, Ans. ABC and DBC are two isosceles triangles, on the same base BC.

Page 52 :
A = B ... (1), , bisector of BC, Proof :In DABD and DACD, , B = C ... ( 2 ), From (1) & ( 2 ), , AB =, AC  DABC an isosceles D le , , A, = 75B, =, C, Chapter, Chapter, –– Triangles, Triangles, \ A= B= C= x, In DABC, A+ B+ C =, 180, x+x+x =, 180, , BD =, CD  DDBC an isosceles D le , AD = AD [ Common side ], , \ DABD ≅ DACD [SSScongruency ], , o, , o, , ii.In DABP and DACP, , AB = AC [isosceles D ABC], , o, , 3x = 180, 180, x = 60o, =, 3, \ A = B = C = 60o, , ABP = ACP, , [angles opposite to equal, sides of triangle are equal], , AP = AP [ Common side ], , DABP ≅ DACP [SAScongruency ], iii.\ BAP =, CAP [ C.P.C.T ], , Exercise 5.3, 7.3, , 1., , 65, 51, , AP bisects A, In DBDP and DCDP, , DABC and DDBC are two isosceles, triangles on the same base BC and, vertices A and D are on the same side, BC. If AD is extended to intersect BC at, P, show that, i. DABD ≅ DACD, ii. DABP ≅ DACP, iii. AP bisect A as well as D, iv. AP is the perpendicular bisector of, BC., A, , BD = CD [ BDCis an isosceles triangle ], DP = DP [ Common side ], \ DBDP ≅ DCDP [SAScongruency ], \ BDP =, CDP [ C.P.C.T ], AP bisects D, \ A bisects A and D, \AP, iv. BPD = CPD [C.P.C.T of Dle BDP ≅ Dle CDP], BPD + CPD =, 180o [Linear Pair], BPD + BPD =, 180o, , D, , B, , P, , 2 BPD = 90o, \ AP is perpendicular bisector of BC, , C, , Ans. Given : DABC and DDBC are two isosceles, triangles on the same base BC., \AB=AC and BD = CD, To prove :, i. DABD ≅ DACD, ii. DABP ≅ DACP, iii.AP bisects A as well as D, iv.AP is the perpendicular, bisector of BC, Proof :In DABD and DACD, AB =, AC  DABC an isosceles D le , BD =, CD  DDBC an isosceles D le , , AD = AD [ Common side ], , \ DABD ≅ DACD [SSScongruency ], ii.In DABP and DACP, , AB = AC [isosceles D ABC], , 2., , Ans., , AD is an altitude of an isosceles triangle, ABC in which AB = AC. show that, i. AD bisects BC, ii. AD bisects A., A, , C, B, D, Given : In an isosceles DABC AB = AC, and AD altitude to BC., To prove :

Page 53 :
AB = PQ [ Given ], AM = PN [ Given ], BM = QN [ proved ], IX, IX Standard, Standard –– Mathematics, Mathematics, \ DABM ≅ DPQN [SSScongruency ], , 66, 52, , ii.In DABC and DPQR, , i.AD bisects BC, ii.AD bisects A, Proof :In DABD and DADC, , [Given ], B = Q [ C.P.C.T ], BC = QR [ Gievn ], \ DABC ≅ DPQR [SAScongruency ], AB = PQ, , AB = AC [isosceles DABC], =, ADB, , = 90o [ AD altitude to BC], ADC, , AD = AD [ Common side ], , 4., , DABD ≅ DADC [ RHScongruency ], BD = CD, , [C.P.C.T ], , Ans., , AD bisects BC, , BE and CF are two equal altitudes of a, triangle ABC. Using RHS congruence,, prove that the triangle ABC is isosceles., A, , BAD = CAD [ C.P.C.T ], , 3., , E, , F, , AD bisects A, Two sides AB and BC and median AM, of one triangle ABC are respectively, equal to sides PQ and QR and median, PN of DPQR. show that :, i. DABM ≅ DPQN, ii. DABC ≅ DPQR, A, P, , C, B, Given : BE and CF are two equal altitudes, of a triangle ABC, Proof : In right angle DBEC and right, angle DCFB, BE = CF, [Given ], BC = BC [ Common side ], , B, Ans., , M, , C Q, , N, ,  AM is median , BM, = MC, = 1 BC , , 2,  of DABC, , PN, is, median, , , QN, = NR, = 1 QR , , 2, D, of, PQR, , , Now BC = QR [ Given ], , 1 BC = 1 QR, 2, 2, =, =, So, BM QN, & MC NR, i.In DABM and DPQN, , =, BEC, , R, , = 90o [BE & CF attitudes], BFC, , \ DBEC ≅ DCFB [ RHScongruency ], \ BCE =, FBC [ C.P.C.T ], , [Sides opposite to equal, , \ AB =, AC angles of Dle are equal], \ ABCis isosceles triangle, 5., Ans., , ABC is an isosceles triangle with AB =, AC. Draw AP perpendicular BC to show, that B = C., A, , AB = PQ [ Given ], , AM = PN [ Given ], BM = QN [ proved ], \ DABM ≅ DPQN [SSScongruency ], ii.In DABC and DPQR, , [Given ], B = Q [ C.P.C.T ], BC = QR [ Gievn ], , AB = PQ, , C, B, P, Given : ABC is an isosceles triangle with, AB = AC. Draw AP perpendicular BC.

Page 54 :
53, 67, , Chapter, Chapter 57 –– Triangles, Triangles, Also, PBC < QCB, , To prove: B = C, Proof :Consider DAPBand DAPC, , To prove:AC > AB, Proof : PBC < QCB Given, , [Given ], AP = AP, [Comon side], APB, = APC, = 90o [ AP ⊥ BC], \ DAPB ≅ DAPC [ RHScongruency ], C [ C.P.C.T ], \ B=, AB = AC, , 180 − PBC > 180 − QCB, ABC > ACB, \ AC > AB, angle, \ Side opposite to greater anfle, is longer, , Exercise 5.4, 7.4, , 1., Ans., , Show that in a right angles triangle, the, hypotenuse is the longest side., , 3., , P, , 5, In Fig.7.49,, B < A and C < D. Show that, AD < BC., B, D, O, A, , R, Q, Let PQR is an right angle triangle, then P + Q + R =, 180o [Sum of the, , angles of, a D is equal to 180o], le, , P + R = 180 − 90 = 90o, Q= P + R, , Ans. In figure, B < A and C < D, To prove:AD < BC, Proof : B < A, , \ Q> P, , [Given ], , A> B, , Q> R, , OB > OA... (1), , [Side opposite to, \ PR > PQ and PR > QR greater angle is larger], , C< D, , \PR is the longest side i.e., hypotenuse is, the longest side of a right angle triangle., 2., , C, , OC > OD ... ( 2 ), From (1) & ( 2 ), , In Fig 7.48,, sides AB and AC of DABC are, 5, extended to point P and Q respectively., Also, PBC < QCB. Show that AC > AB., A, , OB + OC > OA + OD, BC > AD, AD < BC, 4., , B, , C, , Q, P, Ans. Given : Sides AB and AC of DABC are, extended to points P and Q respectively., , AB and CD are respectively the smallest, and longest sides of a quadrilateral, ABCD. Show that ∟, A>∟, C and ∟, B>∟, D

Page 56 :
55, 69, , Chapter 7, 5 –– Triangles, Triangles, Chapter, Ans., , P, , A, , l, C, B, l is a line and A is a point not lying on l. B, and C are points on l, To prove : In DABC, B = 90o, \ Cis an acute angle, \ B> C, AC > AB [Side opposite to greater angle is greater], ⇒ AB < AC, Exercise 5.5, 7.5 (Optional), , 1., , ABC is a triangle. Locate a point in the, interior of DABC which is equidistant, from all the vertices of DABC., Ans. Construct the perpendicular bisector of two, sides of DABC. Their point of intersection, is the required point., A, , P, , R, O, , B, , Q, , Q, 3., , C, , In a triangle locate a point in its interior, which is equidistant from all the sides of, the triangle., Ans. Draw the angle bisectors of any two angles, of the triangle. Their point of intersection, is the required point., , O, , K, , L, , R, , In a huge park, people are concentrated, at three points (see fig 57.52) :, A, , B, C, A : where there are different slides and, swings for children,, B : near which a man-made lake is, situated,, C : which is near to a large parking and, exit., Where should an ice-cream parlor be set, up so that maximum number of persons, can approach it?, (Hint : The parlor should be equidistant, from A, B and C), Ans. Draw the perpendicular bisectors of two, sides. there point of intersection is the, required point., 4., , S, O is the point of intersection of, perpendicular bisectors of two sides., 2., , J, , Complete the hexagonal and star shaped, Rangolies by filling them with as many, equilateral triangles of side 1 cm as you, can. Count the number of triangles in, each case. Which has more triangles?

Page 57 :
56, 70, , IX Standard, Standard –– Mathematics, Mathematics, IX, , Ans. In hexagonal rangoli : Number of, equilateral triangles each of side 5cm = 6, Area of equilateral triangle with side 5cm, 3, 2, =, ( side ), 4, 3, 2, =, × ( 5), 4, 3, =, × 25, 4, Area of hexagonal rangoli, , Total area of star rangoli, =, 12 × area of D le side 5cm,  3, 2, =, × ( 5 ) , 12 × ,  4, , 3, × 25, 4, 3 2, = 300, cm, 4, Number of equilateral each of side1cm, in star rangoli, Area of star rangoli, =, Area of side1cm D le, =12 ×, , = 6 × Area of equilateral D le with side, 5cm, 25 3, 4, 3, = 150, 4, Area of equilateral triangle with side1cm, , = 6×, , 3, 2, ( side ), 4, 3 2, 3, = =, (1), 4, 4, Number of equilateral triangles side1cm, Area of hexagon, =, Area of D le 1 cm, , 3, 4, =, 3, 4, = 300, 300, , =, , 3, 150, 4 150, = =, 3, 4, Now in, is star, Now, starrangoli, rangoli, Number of equilateral triangles each, of side 5cm =12, , Star rangoli has more equailateral D le, each side1cm, Additional Problems, , I., , Multiple Choice Questions, , 1., , The symbol for congruence is, a) ≡, b)~, c) =, d) ≅, , 2., , Two circles are congruent. If the radius, of one circle is 2cm, then the diameter of, the other circle is, a) 2 cm, b) 4 cm c) 0.5 cm d) 3 cm, , 3., , The difference of the lengths of any two, sides of a triangle is, a) equal, b) less than, c) greater than, d) half of the third side, , 4., , Two triangles are congruent, if any, two pairs of angles and one pair of, corresponding angles are equal., a) SAS congruency b) ASA congruency, c) SSS congruency d) AAS congruency

Page 58 :
Also OAC = ODB [ C.P.C.T ], OCA = OBD, if OA = OC, ,  angle opposite to equal, 57, 71 , ,  sides of DOAC, , But OAC = ODB, , Chapter 5, 7 – Triangles, , OAC = OCA, , 5., , In right angle triangle ABC, C is a right, angle then the longest side is, a) AB, b) AC, c) BC, d) None of these, Ans. 1) d, 2) b, 3) b, 4) d, 5) a, Answer the following questions, , 1., , Angles A,B and C of a triangle ABC are, equal to each other. Prove that DABC is, equilateral., Ans. In triangle ABC, A, A, = B, = C, To prove:AB, = BC, = AC, Proof :In DABC, B, C, A = B.... (1), , \ OCA =, ODB, \ AC||BD, 3., , AC = AB... ( 2 ), AB, = BC, = AC, \ ABCis an equilateral triangle, , Ans., , Suppose line segments AB and CD, intersect at 0 in such a way that AO =, OD and OB = OC. Prove that AC = BD, but AC may not be parallel to BD., In DOAC and DODB, OA = OD, OB = OC, AOC = BOD, , [ Given ], [ Given ], [ V.O.A ], , A, , 0, , D, , C, B, , \ DOAC ≅ DODB [S.A.S postulate ], , [ C.P.C.T ], Also OAC = ODB [ C.P.C.T ], [ C.P.C.T ], OCA = OBD, AC = BD, , if OA = OC,  angle opposite to equal , , ,  sides of DOAC, , But OAC = ODB, ODB, \ OCA =, \ AC||BD, OAC = OCA, , B, 2, , 1, D, C, Ans. In triangles ABD and CDB, we have, AB = CD [Given], AD = BC [Given], BD = DB [Common side], DABD ≅ DCDB [S.S.S.Postulate ], , [ C.P.C.T ], , 1= 2, 4., , Ans., , From (1) & ( 2 ), , In the adjoining figure, AB = CD and, AD = BC. Show that 1 = 2., A, , B= C, , 2., , [ C.P.C.T ], , In a triangle ABC, AB = AC and the, bisectors of angle B and C intersect at 0., Prove that BO = CO and AO bisector of, angle BAC., A, , 0, B, C, AB = AC [Given], C = B ( angles opposite to equalsides are equal ), B C, =, 2, 2, Since BO and CO are bisectors of Band C, B C, ABO, = = = ACO, 2, 2, Consider DBCO, OBC = OCB, BO = CO, ( Proved ), ABO = ACO, DABO ≅ DACO, BAO, =, , [SAS postulate], , CAO ⇒ AO bisects A

Page 59 :
58, 72, 5., Ans., , IX, IX Standard, Standard –– Mathematics, Mathematics, , In the figure BCD = ADC and ACB =, BDA. Prove that AD = BC and A = B., A, , B, , 3, , 1, , 2, , 4, , C, We=, have 1 2=, and 3 4, 1+ 3 = 2 + 4, ACD = BDC, ( Given ), ADC = BCD, CD = CD, , ( Common ), , ACD = BDC, , ( Proved ), , D, , \ DACD ≅ DBDC ( ASA Postulate ), \ AD =, BC &, A= B

Page 60 :
127, 59, , Chapter, CHAPTER--11, 6, , Constructions, Constructions, 6.1, Exercise 11.1, Construct an angle of 90o at the initial, point of a given ray and justify the, construction., Ans. Steps of construction, i. Draw a ray OA, ii. With O as centre and convenient radius,, draw an arc LM cutting OA at L., iii. Now with L as centre and radius OL,, draw an arc cutting the arc LM at P., iv. Then taking P as centre and radius OL,, draw an arc cutting arc PM at the point Q., v. Join OP to draw the ray OB. Also join O, and Q to draw the ray OC we observe that, AOB, = BOC, = 60o, vi. Now we have to bisect BOC. For this, , Now join QP ; then, OP = OQ = PQ (By construction), Therefore, DOQP is an equilateral triangle, ∴ POQ which is same as BOCis equal, , 1., , with P as centre and radius greater than 1/2, PQ draw an arc., vii. Now with Q as centre and the same, radii as in step 6. Draw another arc cutting, the arc draw in step 6 at R., viii. Join O and R and draw ray OD., Then AOD is the required angle of 90o., Verification:Measure AOD , you will, see that AOD = 90o., Justification of construction :, Join PL, then, OL = OP = PL [By construction], , ∴DOPL is an equilateral triangle and, POL which is same as BOA is equal, to 60o., D, , C, , B, Q, , 30o, , 30o, 60o, , P, LA, , to 60o.By construction, OD is bisector of, BOC, ∴ DOC =, DOB, 1, = BOC, 2, 1, 30o, =× 600. =, 2, Now, DOA, = BOA + DOB, DOA, = 60o + 30o, DOA = 90o, 2., , Construct an angle of 45o at the initial, point of a given ray and justify the, construction., Ans. Observe that, 1, 45o=, × 90o, 2, We, therefore, follow the procedure of, biseting a given angle to get the required, angle. Thus to construct an angle of 45o ,, we proceed as follows :, Steps of construction :, i. Draw SOL = 90o [Note : Follow the, same steps as done in construction of angle, 90o], ii. With L as centre and radius greater than, 1/2 LS, draw an arc., iii. Now, with S as centre and the same, radius as in step 2., draw another arc, cutting the arc draw in step 2 at F., iv. Join O and F draw ray OE.

Page 61 :
60, 128, , IXStandard, Standard––Mathematics, Mathematics, IX, , Thus, OE bisects SOL, and therefore,, SOE, = SOL, = 45, Verification:Measure SOE, you will, see that SOE 45, Justification of construction:, Join S, then OLSis an isoscels right, triangle right angle at O., ∴ OL =, OS, S, E, , F, , O, L, Therefore, O lies on the perpendicular, bisector of SL., ∴ SF =, FL, and OFS = OFL, Now in DOFSand DOFL, , 3., , Construct the angles of the following, measurements :, o, 1, i.30o, ii.22, iii.15o, 2, Ans. 1. Construction of 30o, 1, Observe that 30= × 60o, 2, We, therefore, follow the procedure, of bisecting a given angle learnt in, construction to get the required angle., Thus to construct an angle of 30o , we, proceed as follows ., Steps of construction :, i. Draw a ray OA, ii. With O as centre and a suitable radius,, draw an arc LM that cuts OA at L, iii. With L as centre and radius OL, draw, an arc to cut LM to N., iv. Join O and N and draw ray OB. Then, AOB = 60o, v. With L as centre and radius greater than, 1/2 LN, draw an arc., vi. Now with N as centre and same radius, as in step 5, draw another arc cutting the, arc drawn in step 5 at P., vii. Join O and P and draw ray OC., B, , OF = OF [ Common side ], OS = OL [ Construction ], , SF = FL, ∴ DOFS ≅ DOFL [S.S.Scongruency], ⇒ SOF =, LOF [ C.P.C.T ], Now,, SOF + LOF =, SOL, ⇒ LOF + LOF =, 90o, ⇒ 2 LOF =, 90o, 1, ⇒ LOF =, × 90o, 2, ⇒ LOF =, 45o, , ( or ) AOE = 45o, , C, M, , P, , N, , O, , L, A, Thus OC bisects AOB, and therefore,, AOC, = BOC, = 30o, Verification:Measure AOC, you willsee, that AOC = 30o, o, , 1, 2, o, 1, 1, Observe that 22 =, × 45o, 2, 2, We therefore, follow the procedure, 2.Construction of 22

Page 62 :
61, 129, , Chapter, – Constructions, Chapter6 11, – Constructions, of bisecting a given angle learnt in, construction to get the required angle., Thus to construct an angle of 22 1/2o we, proceed as follows :, Steps of construction :, i.Draw AOD = 900, ii. Now: bisect, by raysteps, OE such, that in, [Note, FollowAOD, the0 same, as done, i.Draw AODof=90, 90o oin question number 1], construction, = AOE, = 45, DOE, ii. Now bisect AOD, by ray OE such that, = 9000o the arc of circle, iii.Let ray, OE intersect, i.Draw, AOD, [Note, =: Follow, = the, DOE, AOE, 45 same steps as done in, ii., ray OE, such that, atNow, N. bisect AOD, construction, 45o inbyQ.no., 2]of, iii.Let ray OEofintersect, the, arc, circle, o, o, iv., Now with, centre, and radius, =, =L as45, DOE, AOE, at N., iii.Let, ray OE1 intersect, of circle, greater, drawthe, anarc, arc., iv., Nowthan, with LLN,, as centre, and, radius, 2, at N., 1, v.With, N, as centre, and same, radius as in, greater, draw, an arc., iv. Nowthan, with, LLN,, as centre, and, radius, = 900, i.Draw AOD, step 4.Draw 12another arc cutting the arc, v.With, as centre, and, radius, in, ii. Now N, bisect, AOD, bysame, ray OE, suchasthat, greater, LN,, draw inthan, step 42at, I. draw an arc., o arc cutting the arc, step, 4.Draw, another, =, =, DOE, AOE, 45draw, vi.Join, O, I and, ray OF,, thus, v.With, Nand, as centre, and same, radius, asOF, in, draw, inray, step, 4 at, I., iii.Let, OE, intersect, the, arc, of, circle, bisects, AOEanother, and therefore,, step, 4.Draw, arc cutting the arc, vi.Join, and I and draw ray OF, thus OF, at N. =OEOF, AOF, draw in step 4 at I., bisects, AOE and therefore,, iv. Now, o with L as centre and radius, vi.Join, 1 O and I and draw ray OF, thus OF, =AOF, 22 = EOF1, 2 o than, greater, LN,therefore,, draw an arc., bisects, AOE and, 1, 2, Verification:Measure, AOF with, =AOF, 22 = EOF, v.With, 2 oo N as centre and same radius as in o, 1, protractor, we observe that, AOF, = 22, 1, Verification:Measure, withthe, step, cutting, arc 2, =, 22 4.Draw another arcAOF, 2, o, draw in step, at I., 1, protractor, we4observe, that, Verification:Measure, AOFAOF, with= 22 2, D, vi.Join O and I and draw ray, E OF, thus OF oo, 1, protractor, we, observe, that, bisects AOE and therefore,AOF = 22 2, F, N, AOF = EOF, o, , 1, 2 0, D, Verification:Measure AOF with, , = 22, , protractor we observe that AOF = 22 1, , o, , 2, , 3. Construction of 15o, o, 1 × 30o, Observe that15=, 2, We, therefore, follow the steps of bisecting, given angle learnt in construction to get, the required angle., Thus to construct an angle of 15o , we, proceed as follows :, , Steps of construction :, i.Draw AOB = 600, ii. Now bisect AOB by ray OE such that, = AOC, = 30o, BOC, iii.Let ray OCintersect the arc of circle, at Q., iv. Now with L as centre, and radius, i.Draw AOB = 600, 1, greater, draw, an OE, arc.such that, ii., Now than, bisect LQ,, AOB, by ray, 2, o, = QAOC, =, BOC, 30and same radius as in, v.With, as centre, iii.Let, ray, OCintersect, arc ofthe, circle, step 4.Draw another arcthe, cutting, arc, at, Q., draw in step 4 at R., , iv., NowOwith, centre, vi.Join, andLRas, and, drawand, rayradius, OS, thus OS, 1, bisects than, AOC and, greater, LQ,therefore,, draw an arc., 2, COS, = AOS, = 15o, v.With Q as centre and same radius as in, B, Verification:Measure, AOS with, C the arc, step 4.Draw another arc cutting, protractor we observe that AOS = 15o, draw in step 4 at R., S, vi.Join O and R and draw ray OS, thus OS, Q, bisects AOC and therefore,, o, COS, = AOS, =, 0 15 l, A, Verification:Measure AOS with, , protractor we observe that AOS = 15o, , 4., , Construct the following angles and verify, by measuring them by a protractor :, ii. 105o, iii. 135o, i. 75o, o, Ans. Construction of 75 :, Steps of construction :, i.Draw ABE = 600 and ABF = 90o, ii.Let ray, BFintersect, the arc, of circle, (Note, : Follow, the same, steps, as done in, i.Draw ABE, =question, 600 and ABF, = 90o, example, 1, and, no, ., 1), at G., ii.Let ray BFintersect the arc of circle, iii. Now with M as centre and radius, at G., 1, greater, MG,, draw an, iii. Nowthan, with2M, as centre, andarc., radius, iv.With, G as1centre, radius as in, greater than, MG, and, drawsame, an arc., 2, step 3.Draw an arc which intersects the, iv.With G as centre and same radius as in, previous arc at point 4., step 3.Draw an arc which intersects the, v.Draw a ray BC passing through which, previous arc at point 4., bisect EBF, v.Draw a ray BC passing through which, bisect EBF

Page 64 :
131, 63, , Chapter, Constructions, Chapter 11, 6 ––Constructions, In right DADBand right DADC, , B, , AD = AD ( Common ), , D, , ADB = ADC ( each 90o ), , BD = CD ( By construction ), , P, , ∴ DADB ≅ DADC, , N, , C, M O, Because AOD, = AOB + BOD, , ∴ B = C = 60o, Therefore in DABC third agle, , A, , A = 180o − ( B + C ), , = 90o + 45o, , = 180o − ( 60o + 60o ), , = 135o, Verification:Measure AOD by using, protractor you willsee that AOD = 135, , = 180o − 120o, , o, , Construct an equilateral triangle, given, its side and justify the construction., Ans. Steps of construction :, i. Draw a line segment BC of length 6cm., ii.At Bdraw XBC = 60o, , = 60o, Each of three angles of a triangle is, 60o. Hence constructing triangle is an, equilateral triangle., , 5., , iii. Draw perpendicular bisector PQ of line, segment BC., iv. Let A and D be the points where, PQ intersects the ray BX and side BC, respectively., v. Join AC, Thus ABC is the required equilateral, triangle., X A, , P, , B, , D, Q, , Exercise 11.2, 6.2, , 1., , Construct a triangle ABC in which BC =, 7cm, B = 75o and AB + AC = 13 cm., , Ans. Given : In DABC, BC = 7cm, B = 75o and, AB + AC = 13 cm, Required : To construct the traingle ABC, Steps of construction :, 1. Draw the box BC = 7cm., 2. At the point B make an angle XBC =, 75o., 3. Cut a line segment BD equal to AB +, AC (13 cm) from the ray BX., 4. Join DC., x, D, 13c, m, , Q, , C, y, , Justification of construction :, , B, , A, , 75o, 7cm, , C

Page 65 :
64, 132, , IX Standard – Mathematics, line segment QR., , 5.Make on DCY = BDC, 6. Let CY intersect BX at A, Then, ABC is the required triangle., 2., , Construct a triangle ABC in which BC =, 8cm, B = 45o and AB – AC = 3.5 cm., , L, , Ans. Given : In DABC, BC = 8cm, B = 45o and, AB – AC = 3.5 cm., , S, , A, , P, , P, M, , 4. Join SR, 5. Draw the perpendicular bisector LM of, SR, 6. Let LM intersect QX at P, 7. Join PR., Then, PQR is the required triangle., , 4., , cm, , D, 3.5, , 60o, , m, , Q, , 2c, , Required : To construct the triangle ABC, Steps of construction :, 1. Draw the base BC = 8 cm, X, , B, , x, , P, , 45o, , C, Q, , 2. At the point B make an angle XBC =, 45o., 3. Cut the line segment BD equal to AB –, AC from the ray BX., 4. Join DC., 5. Draw the perpendicular bisector, say PQ, of DC., 6. Let it intersect BX at a point A., 7. Join AC, Then, ABC is the required triangle., Construct a triangle PQR in which QR, = 6cm, Q = 600 and PR – PQ = 2cm., Ans. In DPQR, QR = 6cm, Q = 60o and PR – PQ, = 2 cm., Required : To construct the DPQR, Steps of construction :, 1. Draw the base QR = 6cm, 2. At the point Q make an XQR = 60o., 3. Cut line segment QS = PR – PQ from, the line OX extended on opposite side of, , Construct a triangle XYZ in which Y =, 30o , Z = 90o and XY + YZ + ZX = 11 cm., Ans. In triangle XYZ, Y = 30o , Z = 90o and XY, + YZ + ZX = 11 cm., Required : To construct the DXYZ, Steps of construction :, 1. Draw a line segment BC = XY + YZ +, ZX, 2.Make LBC, = Y, = 30o and, MCB, = Z, = 90o, 3.Bisect LBC and MCB.Let these, bisector meet at a point X., D, , L, , M, , x, , 3., , F, B, , 30o, , 90, Y, , 1cm, , Z, , o, , C, , 4. Draw perpendicular bisectors DE of XB, and FG of XC., 5. Let DE intersect BC at Y and FG, intersect BC at Z., 6. Join XY and XZ.

Page 66 :
133, 65, , Chapter 611, – Constructions, Chapter, – Constructions, Then, XYZ is the required triangle., Construct a right triangle whose base, is 12cm and sum of its hypotenuse and, other side is 18 cm., Ans. Given In right DABC, base BC = 12 cm., =, B 90o and AB=, + AC 18cm, , b) If two sides and angle included between, them is given., c) If three sides given, d) If two angles and side between them is, given, , 5., , Required : To construct the right triangle, ABC., Steps of construction :, 1. Draw the base BC = 12 cm., 2. At the point B, make an XBC = 90o., 3. Cut a line segment BD = AB + AC = 18, cm from the ray BX., 4. Join DC, 5. Draw the perpendicular bisector PQ of, CD to intersect BD at a point A., , Construction of a triangle ABC, given, that BC = 6cm, ∟B = 45o is not possible, when difference of AB and AC is equal, to, a) 5.2 cm b) 6.9cm c) 5cm d) 4 cm, Ans. 1) d, 2) a, 3) a, 4) b, Answer the following questions, , 1., , x, 18cm, , 4., , Q, , Ans., , Construct a triangle ABC in which AB =, 5 cm, BC = 4.7 cm, AC = 4.3 cm., C, , 4.3, , cm, , A, , m, cm, 45.7c, , P, , 90o, , C, B, 12cm, 6. Join AC., Then, ABC is the required right triangle., , A, 2., Ans., , Construct a triangle DABC in which AB, = 5 cm, BC = 5 cm and AC = 4.3 cm., C, , 4.3, P, , Q, , cm, , For which of the following condition the, construction of triangle is not possible., a) If two sides and angle included between, them is not given., , Ans., , Construct a triangle PQR in which PQ =, 4 cm, QR = 4.5 cm, ∟, B = 60o., Q, , 4.7, , 3., , To construct a triangle we must know at, least its, parts, a) three, b) two c) one d) Four, , 3., , B, , 5 cm, , cm, , 2., , A, , 4, , Construction of a triangle is not possible, if, a) AB + AC < BC b) AB + AC = BC, c) AB + AC > BC d) (A) and (B) both, , m, , 1., , 5c, , Multiple Choice Questions, , cm, , Additional Exercise, , I., , B, , 5 cm, , 60o, 4.5 cm R

Page 67 :
66, 134, 4., Ans., , IX Standard, Standard –– Mathematics, Mathematics, IX, , Construct a right triangle PQR in which, Q = 90o , QR = 4.5 cm and ∟, R = 50o., ∟, , A, , P, 50o, , 90 50o, Q 4.5 cm R, o, , 5., Ans., , Construct a triangle PQR whose, perimeter is 13 cm and whose sides are, in the ratio 2 : 3 : 4., P, , Ans., , Ans., , L, , M, , N, , Q, L, , M, , Y, N, , Construct triangle ABC perimeter is, 13.5 cm and whose angles are 60o and, 75o., A, , 60o, X, , 8., Ans., , 60o, B, , 75o, , 75o, C, , Ans., , 80o, , B, , C, , Y, , Construct, triangle, ABC, whose, perimeter is 12.5 cm and whose base, angles are 50o and 80o., , Y, , Construct a triangle XYZ in which YZ, = 4.5 cm, ∟, Y = 60o and sum of other two, sides is 7.5 cm., M, , 60o, Y 4.5 cm Z, , R, P, , 9., , 80o, , 7.5 cm, X, , Y, , Construct a triangle PQR, whose, perimeter is 15 cm and whose sides are, in the ratio 3 : 4 : 6, , X, , 7., , Q, , P, , X, , 6., , X, , 50o

Page 68 :
73, 67, , Chapter, CHAPTER - 8, 7, , Quadrilaterals, Key Points :, , ●, ●, ●, ●, ●, , Quadrilateral : A linear figure on a plane consisting of four line segments which are placed in, an ordered way such that the adjacent segments meet only a their end points., Convex quadrilaterals : A quadrilateral in which each interior angle is less than 180o ., Concave quadrilaterals : A quadrilateral in which some interior angle exceeds 180o ., Diagonal : The line segment joining opposite vertices of quadrilateral., Sum of the angles of quadrilateral is 3600, , Types of quadrilaterals, , i. Trapezium : It is quadrilateral in which one pair of opposite sides are parallel., ii. Parallelogram : A quadrilateral in which both the pairs of opposite sides are parallel., iii. Rectangle : It is a parallelogram in which measure of all angles are right angles., iv. Rhombus : A rhombus is a parallelogram in which all the four sides are equal., v. Square : A quadrilateral in which all the angles are equal and all the side are equal., vi. Kite : It is quadrilateral in which two isosceles triangles are joined along the common base., ●, In a parallelogram, i. Opposite sides are equal, ii. Opposite angles are equal, iii. Diagonals bisect each other, ●, Diagonals of a rectangle bisect each other at right angles., ●, Diagonals of a square bisect each other at right angles and are equal, ●, The line-segment joining the mid points of any two sides of a triangle is parallel to the third, side and is half of it., A line through the mid-point of a side of a triangle parallel to another side bisects the third side., ●, ●, The quadrilateral formed by joining the midpoints of the sides of a quadrilateral in order, is a, parallelogram., ●, A diagonal of a parallelogram divides it into two congruent triangles.

Page 69 :
∴ DACB ≅IX, DBDA, [SSScongruent, ], Standard, Mathematics, IX Standard, –– Mathematics, ABC = BAD ... (1) [ C.P.C.T ], , 68, 74, Exercise 7.1, 8.1, , Opposite sides of, , Again AD||BC , ,  parallelogram ABCD , ∴ BAD + ABC =, 180o ... ( 2 ), , 1., , The angles of quadrilateral are in the, ratio 3 : 5 : 9 : 13. Find all the angles of, the quadrilateral., Ans. Let ABCD is a quadrilateral in which, A: B: C: D = 3:5:9:13 (or), A: B: C: D = 3x:5x:9x:13x, , From (1) & ( 2 ), BAD, = ABC, = 90o, A = 90o, ∴ Parallelogram ABCD is a rectangle, , A+ B+ C+ D =, 360o, 3x + 5x + 9x + 13x =, 360o, , 3., , 30x = 360o, 360, x = 12o, =, 30, , Ans., , Show that if the diagonals of a quadrilateral, bisect each other at right angles, then it is, a rhombus., , D, , C, , x = 12o, angle are, angles, are, A =3x =3 × 12 =36o, B =5x =5 × 12 =60, , O, , C =9x =9 × 12 =108o, D = 13x = 13 × 12 = 156o, ∴ Angles of qudrilaterals 36o , 60o ,, 108o &156o, 2., Ans., , If the diagonals of a parallelogram are, equal, then show that it is a rectangle., D, , C, , A, B, Given : ABCD is a quadrilateral where, diagonals AC and BD intersect each other, at right angles at 0., To prove : Quadrilateral ABCD is a, rhombus., Proof :, In DBOC and DCOD, OB = OD, , [Given ], , OC = OC [ Common side ], BOC, =, , COD, = 90o [ Given ], , DBOC ≅ DCOD [SAScongruent ], A, B, Given : In parallelogram ABCD, AC = BD., , ∴ BC =, CD, , ... (1), , Similarly we can prove, CD = AD, , ... ( 2 ), , Proof : In DACB and DBDA, AC = BD [Given], AB = AB [Common side], , AD = AB, , ... ( 3), , AB = BC, , ... ( 4 ), , ∴ DACB ≅ DBDA [SSScongruent ], , AB, = BC, = CD, = AD, ∴ ABCD is a rhombus., , To prove : Parallelogram ABCD is a rectangle, , BC = AD [Opposite sides of a parallelogram], , ABC = BAD ... (1) [ C.P.C.T ], Opposite sides of, , Again AD||BC , ,  parallelogram ABCD , ∴ BAD + ABC =, 180o ... ( 2 ), From (1) & ( 2 ), o, , From (1)( 2 )( 3) & ( 4 )

Page 72 :
71, 77, , Chapter 87 –– Quadrilaterals, Quadrilaterals, Chapter, 8., Ans., , ABCD is a rectangle in which diagonal AC bisects A as well as C. Show that :, i. ABCD is a square, ii. Diagonal BD bisects B as well as D., , ABCD is a rectangle A & C are, angular bisector of AC., To prove:, i.ABCD is a square, ii.Diagonal BD bisects Band D, Proof :AB||CD, DCA = CAB.... (1), CAD = CAB... ( 2 ), , D, , C, , A, , B, , [Opposite sides of a Rectangle], [ Alternate angles], [ AC angular bisector of A ], , From (1) & ( 2 ), DCA = CAD, , [Sides opposite to equal angles of a triangle are equal], , CD, ∴ AD =, ABCD is a square, ii.In DBDA and DDBC, , [Common side], AD = BC [sides of a square ], AB = CD [sides of a square ], DBDA ≅ DDBC [SSScongruency ], ∴ ABD =, CDB [ C.P.C.T ], ∴ CDB =, CBD [ angles opposite to equal angles of a triangle are equal], BD = BD, , ∴BD bisects B, Now ABD = CDB, , 9., , ABD = ADB, , [ AB = AD ], , CBD = CDB, CDB, ∴ ADB =, ∴ BD bisects D, , [ BC = CD ], , In parallelogram ABCD, two points P and Q are taken on diagonal BD such that DP =, BQ. show that :

Page 74 :
∴ ABED is a parallelogram, AD = BE and AD|| BE ... (1), ii. Again, Quad BEFC, , Chapter 87 –– Quadrilaterals, Quadrilaterals, Chapter, , BE = CF and BE || CF, ∴ BEFC is a parallelogram, iii.CF = BE and CF|| BE ... ( ii ), , Ans. ABCD is a parallelogram and AP and CQ, are perpendicular from vertices A and C., On diagonal BD respectively, To prove :, , From (1) and ( 2 ) we get, AD = CF and AD|| CF, , i. DAPB =, DCQD, , iv.∴ ACFD is a parallelogram[∴ If one, , ii. AP = CQ, , pair of opposite sides of quadrilateral is, , Proof :In DAPB and DCQD, , equal and parallel, It is a parallelogram], , AB = CD [Opposite sides of parallelogram], ,  Opposite sides , ,  of parallelogram , , v. Hence AC = DF , , ABP = CDQ [ Alternate angles ], APB, =, , CQD, = 90 [ AP & CQ perpendicular ], , vi. In DABC and DDEF, , o, , AB = DE [ Given ], , ∴ DAPB ≅ DCQD [ ASA congruency ], , BC = EF [ Given ], , ii. AP = CQ [ C.P.C.T ], , 11., , In DABC and DDEF, AB = DE , AB ||, DE, BC = EF and BC || EF . Vertices A,, B and C are joined to vertices D, E and, F respectively. Show that, A, D, B, , 73, 79, , AC = DF [ Form ( v )], DABC ≅ DDEF [SSS congruency ], , 12., , ABCD is trapezum in which AB || CD, and AD = BC . Show that, B, A, E, , C, , F, E, i. Quadrilateral ABED is a parallelogram, ii. Quadrilateral BEFC is a parallelogram, iii. AD || CF and AD = CF, iv. Quadrilateral ACFD is a parallelogram, v. AC = DF, vi. DABC ≅ DDEF, Ans. In DABC and DDEF, AB = DE and AB||DE, BC = EF nad BC|| EF, i. In quadrilateral ABED, its one pair of, opposite sides AB and DE are such that, AB = DE and AB|| DE, ∴ ABED is a parallelogram, , A+ E =, 180o, =, A 180 − E ... ( i ), Since AB|| CD and AD|| CE, , [Opposite sides of, , AD = BE and AD|| BE ... (1) parallelogram are, ii. Again, Quad BEFC, , D, C, i. A = B, ii. C = D, iii. DABC ≅ DBAD, iv. Diagonal AC = diagonal BD, iv.Diagonal AC = diagonal BD, [Hint :- Extend AB and draw a line through C, [Hint, :- Extend, AB and draw, line], parallel, to DA intersecting, ABaproduced, at E], Ans. Given : Extend AB and draw a line CE, parallel to AD as shown in the figure. AD ||, CE and transversal AE. Cuts them at A and, Join AC and, BDAC and BD, E .respected, . Join, , equal & Parallel], , BE = CF and BE || CF, ∴ BEFC is a parallelogram, iii.CF = BE and CF|| BE ... ( ii ), From (1) and ( 2 ) we get, AD = CF and AD|| CF, iv.∴ ACFD is a parallelogram[∴ If one, , ∴ AECD is a parallelogram, AD = CE, =, BC CE, =, [ AD BC Given ], Thus, in DBCE, we have, BC = CE, ,  Equal angles opposite , ,  to equal sides, , , CBE = CEB , o, , 180 − B =, E, o

Page 75 :
∴ AECD is a parallelogram, AD = CE, =, BC CE, =, [ AD BC Given ], , 80, 74Thus, in DBCE, we have, , IX, IX Standard, Standard –– Mathematics, Mathematics, , BC = CE, , 1, i.SR ||AC and SR = AC, 2, ii.PQ = SR, iii.PQRS parallelogram, ,  Equal angles opposite , ,  to equal sides, , , CBE = CEB , o, , 180 − B =, E, CBE + ABC =, 180 [ Linear pair ], o, , o, , ∴ CBE =180 − ABC, o, 180 − E =, B, , ... ( ii ), , From ( i ) and ( ii ) we get A = B, , ii.ABCD is a trapezium AB||CD, ∴ A+ D =, 180o ... ( iii ), B+ C =, 180o, , ... ( iv ), , Two parallel lines sum of interior angles , , o , on the same side of a transversalis180 , Equating ( iii ) & ( iv ), A+ D = B+ C, A+ D = A+ C, , [A=, , Bin Part i ], , D= C, (or) C = D, iii.In DABC and DBAD, , AB = AB [ Common side ], A = B  Proved ( i ) , BC = AD [ Given ], , DABC ≅ DBAD [SAScongruency ], iv.AC = BD, , Ans. ABCD is a quadrilateral in which P,Q,R,S, are mid-point of sides AB,BC, CD & AD., AC is diagonal, To prove :, i.SR ||AC and SR = 1/ 2 AC, ii.PQ = SR, iii.PQRSis a parallelogram, Proof :, i.In DDAC, Sis the mid − point AD and R is the, mid − poin CD, ∴ SR ||AC and, Mid point theorem, SR = 1 AC, 2, ii.In D BAC, P is the midpoint ABand Q is the, midpoint BC, ∴ PQ||AC, Mid point theorem, and PQ = 1 AC .. (1), 2, 1, SR = AC... ( 2 )  From ( i ) , 2, From (1) & ( 2 ), , [C.P.C.T ], , PQ = SR, , In trapezium ABCD diagonal AC, AC = diagonal BD, , iii.PQ||AC ... ( 3)  From ( ii ) , SR ||AC... ( 4 ),  From ( i ) , , Exercise 7.2, 8.2, , 1., , SR from ( 3) & ( 4 ), , ABCD is a quadrilateral in which P,Q,R, and S are mid-points of the sides AB,, BC, CD and DA. AC is a diagonal. Show, that :, , PQ||SR, Also PQ = SR, ∴ PQRSis a parallelogram, 2., , Ans., , ABCD is a rhombus and P,Q,R and, S are mid-points of the sides AB, BC,, CD and DA respectively. Show that the, quadrilateral PQRS is a rectangle.

Page 76 :
75, 81, , Chapter87––Quadrilaterals, Quadrilaterals, Chapter, D, S, , R, , A, , C, 3, P, , 4, 1, , 2, , Q, , B, P,Q,R and S are the mid points of respective sides AB, BC, CD and DA of rhombus PQ, QR., RS and SP are joined., To prove : PQRS is a rectangle, Construction : Join A and C, Proof :, In DABC, P is the mid − points of ABand Q is the mid − point of BC, ∴ By mid −point, poin theorem, PQ || AC and PQ = 1 AC ... ( i ), 2, In DADC, R is the mid − point of CD and Sis the mid − point of AD, 1 AC ... ( ii ), ∴ SR ||AC and SR =, 2, From ( i ) & ( ii ) we get PQ||SR & PQ = SR, ∴ PQRSis a parallelogram, Now ABCD is Rhombus ( Given ), AB = BC, 1 AB = 1 BC, 2, 2, PB = BQ, PQ, 1= 2, , [angles opposite to equalsides of triangle are equal], , In DAPSand DCQR, AP = CQ, AP = CQ, ,  AB, = BC, = 1 AB, = 1 BC , 2, 2, , , P, &, Q, are, mid, points, of, AB&, BC], [, , Similarly AS = CR, PS = QR, DAPS ≅ DCQR, , [Opposite sides of parallelogram ], [SSScongruency], , 3 = 4 [ C.P.C.T ], We have, 1 + SPQ + 3 =, 180o, and 2 + PQR + 4 =, 180o, , [ Linear pair ]

Page 77 :
2, In DADC, R and Sare the mid − points, of CD and AD respectively, 1 AC... ( 2 ), ∴ SR ||AC and SR =, 2 –– Mathematics, IX Standard, Standard, Mathematics, IX, From ( i ) & ( ii ), , 76, 82, , PQ||SR and PQ = SR ... ( 3), , ∴ 1 + SPQ + 3 = 2 + PQR + 4, 1, =, , 2=, &3, , PQRSis a parallelogram, ABCD is a rectangle, AD = BC, 1 AD = 1 BC, 2, 2, AS = BQ ... ( 4 ), , 4, , PQR, ∴ 1SPQ, =, ) +4, PQR, + SPQ, + 3 = 2...+( iii, Now,, PQRSis, 1 2=, & 3 4 a parallelogram, =, SPQ, PQR, 180...o ( iii...) ( iv ), +=, =, SPQ, PQR, ∴, , [SP, || (QR, and, cuts then and the sum, From, iii ) &, Now,, PQRSis, ( ivaPQ, )parallelogram, of interior angles oon, the same side of a, o, SPQ + SPQ, PQR =, 180 ... ( iv ), =, 180, transversal is 180o], From, ) & (oiv ), 2 SPQ( iii, = 180, , In DAPSand DBPQ, AP = BP ( P is mid point of AB ), PAS = PBQ, , o, SPQ += 90, SPQ, 180o, =, , AS = BQ, , 2 SPQPQRSis, = 180o a parallelogram whose, Thus,, , AS = BQ, , o, one, = 90o.Hence , PQRSis, SPQangle, = 90SPQ, , DAPS ≅ DBPQ [SAScongruency ], , rectangle., Thus,, PQRSis a parallelogram whose, , PS = PQ [ C.P.C.T ] ... ( v ), , one angle SPQ = 90o.Hence , PQRSis, , From ( iii ) and ( v ) PQRSis a parallelogram, , rectangle., 3., , Ans., , ABCD is a rectangle and P,Q,R and S, are mid-point of the sides AB, BC, CD, and DA respectively. Show that the, quadrilateral PQRS is a rhombus., D, , R, , S, A, , C, Q, , P, , each 90o ,  From ( 4 ) , , PS = PQ [ two adjacent sides are equal], Hence, PQRSis rhombus, 4., , ABCD is a trapezium in which AB || DC,, BD is a diagonal and E is the mid point, of AD. A line is drawn through E parallel, to AB intersecting BC at F. Show that F, is the mid-point of BC., , B, , Rectangle ABCD in whichP,Q,R and S, are mid-points of sides AB, BC, CD and, DA respectively PQ, QR, RS and SP are, joined., To prove : PQRS is a rhombus, Construction : Join AC, Proof :, In DABC, P and Q are mid − points osf, sides AB, BC, 1 AC ... (1), ∴ PQ||AC and PQ =, 2, In DADC, R and Sare the mid − points, of CD and AD respectively, 1 AC... ( 2 ), ∴ SR ||AC and SR =, 2, From ( i ) & ( ii ), , G, , Ans. Given : ABCD is a trapezium in which AB, || CD, BD is a diagonal and E is the mid, point of AD. A line is drawn through E, parallel to AB intersecting BC at F., To prove : F is the mid-point of BC., Proof : Let BD intersect EF at G, In DDAB, , ∴ E is the mid point of AD and EG || AB, ∴ G is the mid point BD, , [ By converse of mid point theorem ], , PQ||SR and PQ = SR ... ( 3), , In DBDC, , PQRSis a parallelogram, ABCD is a rectangle, , ∴ G is the mid − point of BD and, GF || AB || CD

Page 79 :
78, 84, 7., , IX Standard – Mathematics, IX Standard – Mathematics, , ABC is a triangle right angled at C. A line through the mid-point M of hypotenuse AB, and parallel to BC intersects AC at D. Show that, i.D is the mid − point of AC, ii.MD ⊥ AC, 1, iii.CM, = MA, = AB, 2, , Ans., , A, , M, , B, i.In DABC, M is the mid point of AB ( Given ), MD||BC, , 1 D, , 2, , C, , [Converse of mid point theorem ], , AD = CD, , Thus, D is the mid point of AC, ii.l||BC, l, l= C, , [Corresponding angles of a transversal], ( Given ), ,  C 90, l 90, =, =, Thus MD ⊥ AC, iii.In DAMD and DCMD, o, , o, , AD = DC  Proved ( i ) , each = 90o , MD = MD [ Common side ], 1= 2, , DAMD ≅ DCMD [SAScongruency ], AM = CM ... (1) [ C.P.C.T ], Given that M is the mid − point of AB, 1 AB... ( 2 ), ∴ AM =, 2, Using (1) & ( 2 ), CM = 1 AB, 2, , l

Page 80 :
79, 85, , Chapter 87 –– Quadrilaterals, Quadrilaterals, Chapter, Additional Problems, , I., , Multiple Choice Question s, , 1., , The sum of the angles of quadrilateral is, b) 180o c) 540o d) 720o, a) 360o, , 2., , The bisectors of angles of a parallelogram, from a, a) Trapezium, b) Rectangle, c) Rhombus, d) Kite, , 3., , If diagonals of a quadrilateral bisect, each other at right angles, then it is a, a) Parallelogram, b) Square, c) Rhombus, d) Trapezium, , 4., , The line segment joining the mid - points, of two sides of a triangle is parallel to, the third and, of it, a) equal, b) one third, c) half, d) one fourth, , 5., , The angle between the diagonals of a, rhombus is, b) 90o c) 30o d) 60o, a) 45o, , 6., , If both the pairs of opposite sides of, a quadrilateral are parallel, then the, quadrilateral is a, a) Parallelogram, b) trapezium, c) Kite, d) Rhombus, , 7., , If one angle of a parallelogram is 90o, and all side are equal, then it called a, a) Rectangle, b) Square, c) Rhombus, d) Kite, , 8., , In a parallelogram ABCD, if ∟, A = 70o, then the measure of ∟, B is, a) 10o, b) 20o c) 90o d) 110o, , 9., , A quadrilateral whose all the four sides, are equal but all the four angles are not, equal is called, a) Square, b) Rhombus, c) Rectangle, d) Parallelogram, , 10., , Which of the following is false, a) A square is a rectangle, b) A square is a rhombus, , c) A parallelogram is a trapezium, d) A kite is a parallelogram, Ans. 1) a, 2) b, 3) c, 4) c, 5) b, 6) a, 7) b, 8) d, 9) b, 10) d, II. Answer the following questions, , 1., , Diagonals of a quadrilateral ABCD bisect, each other. If ∟, A = 35o , determine ∟, B., Ans. Since diagonals of a quadrilateral bisect each, other ABCD is a parallelogram., D, C, 0, 35o, A, B, o, A+ B=, 180, 35o + B =, 180o, B = 180o − 35o = 145o, B = 145o, , 2., , E is the mid-point of the side AD of the, trapezium ABCD with AB || CD. A line, through E draw parallel to AB intersect, BC at F. Show that F is the mid point of, BC., Ans. Given : ABCD is a trapezium in which E is, the mid - point of side AD. Also AB || CD and, EF || AB., A, B, G, F, E, D, C, To prove : F is mid-point of BC, Proof : E is mid-point of AD, AB || CD, AB || EF, EF || CD

Page 81 :
80, 86, , IX Standard – Mathematics, , EG || DC, So in DADC, G will be the, [Converse of mid point, mid point of AC ...(1), theorem], In DACB, GF | AB and G is the mid point of AC, F will be mid point of BC, 3., Ans., , A diagonal of a parallelogram bisects, one of its angles. Show that it is a, rhombus., A, , 1, , B, , 2, , 3, D, C, ABCD is a parallelogram in which AC, bisects ∟, A, To prove : ABCD is a rhombus, Proof :, 1 = 4.... ( i ) [AD || BC, Alternate angles], 1 = 2.... ( ii ) [Angle A bisects], From ( i ) & ( ii ), 2= 4, Now, In DABC 2 =, 4, AB = BC [Sides opposite to equalsides ], Opposite sides of a , =, =, AB CD, and AD BC , ,  parallelogram , = BC, = CD, = AD, AB, Hence, ABCD is a rhombus, , Ans., , ABCD is a rectangle in which diagonal, BD bisects ∟, B. Show that ABCD is a, square., A, , 1= 2, , [ BD bisects B], , 2= 4, CD = BC... (1), AB = CD... ( 2 ), , Sides opposite to equal ,  angles in DCBD , , , , and AD = BC, From ( i ) & ( ii ), AB, = BC, = CD, = DA, , 4, , 4., , To prove : ABCD is a square, Proof :, 1 = 4 [ Alternate angles ], , 1, , 2, , B, , 3, 4, D, C, Given : ABCD is a rectangle and diagonal, BD bisects ∟, B, , and A, = B, = C, = D, = 90o, Hence, ABCD is a square

Page 82 :
188, , 81, , Appendix, Appendix -- 1, 1, Exercise A 1.1, 1., , State whether the following statements are, always true, always false or ambiguous., Justify your answers., (i) There are 13 months in a year., (ii) Diwali falls on a Friday., (iii) The temperature in Magadi is 26°C., (iv) The earth has one moon., (v) Dogs can fly., (vi) February has only 28 days., Ans. i. False because there are 12 months in a year., ii. Ambiguous. At some time in the given year,, Diwali may or may not fall on a Friday., iii. Ambiguous, temperature in magadi, sometimes in a day may not be 26o C., iv. Always true., v. Always False, Dogs can’t Fly., vi. Ambiguous, In a leap year, Febuary has 29, days., 2., , State whether the following statements are, true or false. Give reasons for your answers., (i) The sum of the interior angles of a, quadrilateral is 350°., (ii) For any real number x, x2 ≥ 0., (iii) A rhombus is a parallelogram., (iv) The sum of two even numbers is even., (v) The sum of two odd numbers is odd., Ans. i. False, the sum of the interior angles of a, quadrilateral is 360o., ii. True, iii. True, iv. True, v. False, sum of the two odd number is always, even Eg : 9 + 15 = 24., 3., , Restate the following statements with, appropriate conditions, so that they become, true statements., (i) All prime numbers are odd., (ii) Two times a real number is always even., (iii) For any x, 3x+l >4., (iv) For any x, x3 ≥ 0., (v) In every triangle, a median is also an, , angle bisector., Ans. i. All prime numbers greater than 2 is are odd., ii. Two times a natural number is always even., iii. For any value of x > 1, 3x + 1 > 4, iv. For any value of x ≥ 0, x3 ≥ 0, v. In an equilateral triangle, a median is an, angle bisector., Exercise A1.2, 1., , 1. Use deductive reasoning to answer the, following:, (i) Humans are mammals. All mammals are, vertebrates. Based on these two statements,, what can you conclude about humans?, (ii) Anthony is a barber. Dinesh had his, hair cut. Can you conclude that Antony cut, Dinesh’s hair?, (iii) Martians have red tongues. Gulag is a, Martian. Based on these two statements,, what can you conclude about Gulag?, (iv) If it rains for more than four hours on, a particular day, the gutters will have to, be cleaned the next day. It has rained for 6, hours today. What can we conclude about, the condition of the gutters tomorrow?, (v) What is the fallacy in the cow’s reasoning, in the cartoon below?, Ans. i. Humans are vertebrates, ii. No, Dinesh could have got his hair cut by, any body., iii. Gulag has a red tongue., iv. We conclude that the gutter will have to, cleaned tomorrow., v. All animals having tails need not be dogs for, example, animals such as buffalos, monkeys,, ox etc, have tails but are not dogs., 2., Once again you are given four cards. Each, card has a number printed on one side and, a letter on the other side. Which are the only, two cards you need to turn over to check, whether the following rule holds?, “If a card has a consonant on one side, then, , it has an odd number on the other side.

Page 83 :
82, Appendix, U number, 8, itBhas 3an odd, on the other side.”, Ans. You need to turn over B and 8. If B has an even, number on the other side, then the rule has been, broken. Similarly if 8 has a constant on the, other side, then the rule has been broken., Exercise A1.3, 1., , Take any three consecutive even numbers, and find their product; for example, 2x4x6, = 48,4*6x 8 = 192, and so on. Make three, conjectures about these products., Ans. Three possible conjectures are, i. The product of any three consecutive even, numbers is divisible by 3, ii. The product of any three consecutive even, number is divisible by 4., iii. The product of any three consecutive even, numbers is divisible by 6., 2., Go back to Pascal’s triangle., Linel :l = ll°, Line2: 1 1=111, Line3:l 2 1 = 112, Make a conjecture about Line 4 and Line, 5. Does your conjecture hold? Does your, conjecture hold for Line 6 too?, Ans. Line 4 : 113 = 1331, Line 5 : 114 = 14641, Line 6 : 115 ≠ 15101051, 116 ≠ 1615201561, The conjecture holds for line 4 and line 5, No, because 115 ≠ 15101051, 3., Let us look at the triangular numbers (see, Fig.A 1.2) again. Add two consecutive, triangular numbers. For example, T1 + T2 =, 4, T2 + T3 = 9, T3+ T4 = 16., What about T4 + T5 ? Make a conjecture, about Tn-1 +Tn., Ans. T4 + T5 = 25 = 52, Tn-1 + Tn = n2, 4., Look at the following pattern:, 12=1, 112=121, 1112= 12321, llll2 =1234321, 111112= 123454321 Make a conjecture about, each of the following:, 1111112 =, 11111112= Check if your conjecture is true., Ans. Using above pattern, 1111112 = 12345654321, 11111112 = 1234567654321, , IX Standard – Mathematics, , 189, , 5., , List five axioms (postulates) used in this, book., Ans. 1. A straight line may be drawn from any one, point to any other point., 2. A terminated line can be produced, indefinitely., 3. A circle can be drawn with any centre and, any radius., 4. All right angles are equal to one another., 5. If a straight line falling on two straight lines, makes the interior angles on the same side of it, taken together than two right angles, then the, two right angles., Exercise A1.4, , 1., , Find counter-examples to disprove the, following statements:, (i) If the corresponding angles in two, triangles are equal, then the triangles, are congruent., (ii) A quadrilateral with all sides equal, is a square., (iii) A quadrilateral with all angles equal, is a square., (iv) For integers a and b, a 2 + b 2 =a + b, , (v) 2n2 + 11 is a prime for all whole, numbers n., (vi) n2 - n + 41 is a prime for all positive, integers n., Ans. i. Two triangles with the same, corresponding angles but of different sides, are not congruent., ii. A rhombus has equal sides but may not, be a square., iii. A rectangle has equal angles but may, not be a square., iv. For a = 3 and b = 4, the statement is, not true., v. For n = 11, 2n2 + 11 = 253 is not a prime., vi. For n = 41, n2 - n + 41 is not a prime., 2., , Take your favourite proof and analyse, it step-by-step along the lines discussed, in Section A 1.5 (what is given, what has, been proved, what theorems and axioms, have been used, and so on).

Page 84 :
83, , Appendix - 1, , 190, , Ans. The sum of the interior angles triangle is, 180o, In DABC ∟, A+∟, B+∟, C = 180o, A, D, E, , B, C, Construction : DE || BC, DAB = ABC & EAC = ACB, [alternate angles], DAB + BAC + CAE = 180 [Linear pair], Substitute equation (2) in (1), A+∟, B+∟, C = 180o, ∟, Step 1 :- Theorem is concerned with, property of triangle., Step 2 :- Properties of angles and fact DE, parallel to BC., Step 3 :- Linear pair axion, Step 4 :- by simplification, Step 5 :- Hence theorem is proved, 3., , Prove that the sum of two odd numbers, is even., Ans. Let x and y be two odd numbers. Then x =, 2m + 1 for some natural number m and y =, 2n+1 for some natural number n., x + y = 2m + 1 + 2n + 1, = 2m + 2n + 2, = 2(m + n + 1), There for x + y is divisible by 2 and is, even., 4., , Prove that the product of two odd, numbers is odd., Ans. Let x and y be two odd numbers such that x, = 2m+1 , m ∈, e N and y = 2n + 1, n∈eN, Then xy = (2m + 1)(2n + 1), = 4mn + 2m + 2n + 2, = 2(2mn + m + n) + 1, \xy is not divisible by 2, and so it is odd., 5., , Prove that the sum of three consecutive, even numbers is divisible by 6., Ans. Let 2n, 2n + 2 and 2n + 4 be three, consecutive even number. Then their sum, is 6(n+1) which is divisible by 6., , IX Standard – Mathematics, 6., , Prove that infinitely many points lie on, the line whose equation is y = 2x. (Hint:, Consider the point (n, 2ri), n for any, integer n.), Ans. Consider the points (n, 2n) ; n ∈ z, \It satisfies the equation y = 2x, \Infinitely many points lie on the line, whose equation is y = 2x., 7., , You must have had a friend who must, have told you to think of a number and, do various things to it, and then without, knowing your original number, telling, you what number you ended up with., Here are two examples. Examine why, they work., (i) Choose a number. Double it. Add, nine. Add your original number. Divide, by three. Add four. Subtract your, original number. Your result is seven., (ii) Write down any three-digit number, (for example, 425). Make a six-digit, number by repeating these digits in the, same order (425425). Your new number, is divisible by 7,11 and 13., Ans. i. Let the original number be n. Then we, are doing following operations., n → 2n → 2n + 9 + n = 3n + 9, 3 ( n + 3), , n +3, =, 3, → n +3+ 4 = n + 7 →, n+7−n =, 7, ii. Note that 7 x 11 x 13 = 1001. Take any, three digit number say abc. Then abc x, 1001 = abc abc. Therefore, the six digit, number abcabc is divisible by 7,11 and 13, →

Page 85 :
Blank

Page 86 :
84, , 135, , CHAPTER--12, 8, Chapter, , Heron’s Formula, Formula, Heron’s, Key Points :, , ●, ●, , Heron’s formula is used to find the area of triangle whose sides a,b and c are given., Heron’s formula given by ‘Heron’, Area of traingle = s ( s − a )( s − b )( s − c ), , Where s =, , a+b+c, 2, , ●, ●, , Some other formula’s to find area of triangle, Formula to find area of a right angle triangle, Area of traingle =1 × base × height, 2, = 1 bh, 2, , ●, , Formula to find area of a equilateral triangle =, , ●, ●, , ●, , 3a 2, 4, , Area of quadrilateral whose sides and one diagonal are given area can be calculated by using, Heron’s formula., Formula to find area of an isosceles triangle with base b and equal side a is given, b, a + b + c a + a + a 3a, Area, 4a 2 − b 2, =, =, s = =, 4, 2, 2, 2, ∴, Area, of, signal, board, Unit used to represent area is square units., , Exercise 12.1, 8.1, , 1., , A traffic signal board, indicating ‘School, Ahead’, is an equilateral triangle with, side ‘a’. Find the area of the signal, board, using Heron’s formula. If its, perimeter is 180 cm, what will be the, area of the signal board?, Ans. Given : a = a, b = a & c = a, a + b + c a + a + a 3a, s = =, =, 2, 2, 2, ∴ Area of signal board, =, , s ( s − a )( s − b )( s − c ), 3a  3a,   3a,   3a, ,  − a  − a  − a , 2 2, 2, 2, , , , , =, =, , 3a  3a − 2a   3a − 2a   3a − 2a , , , , , , =, , s ( s − a )( s − b )( s − c ), , 3a  3a,   3a,   3a, ,  − a  − a  − a , 2 2,  2,  2, , , =, =, , 3a  3a − 2a   3a − 2a   3a − 2a , , , , , 2  2  2  2 , 3a a a a, × × ×, 2 2 2 2, , =, , Area of signal board, =, Perimeter = 180 cm, a+b+c =, 180, a+a+a =, 180, 3a = 180, 180, =, a = 60 cm, 3, , 3a 4, =, 16, , 3a 2, 4

Page 87 :
=, , 2, , × × ×, 2 2 2, , 3a 4, =, 16, Chapter, 8 – Heron’s, Formula, Perimeter, 180, cm, =, 136, a+b+c =, 180, a+a+a =, 180, Area of signal board, =, , 12 × 12 × 11× 11× 10 × 10, 10 Standard – Mathematics, = 12 × 11× IX, 85, , =, , = 1320 m 2, , Rent for12 months1m 2 = 5000, 5000, Rent for1month1m 2 =, Rs, 12, Rent for 3months1320 m 2, 5000, =, × 1320 × 3, 12, = 16,50, 000 Rs, , 3 2, a, 4, , 3, 2, ( 60 ), 4, 3, =, × 3600, 4, = 900 3cm 2, =, , 2., , The triangular side walls of a flyover, have been used for advertisements., The sides of the walls are 122m, 22m, and 120m. The advertisements yield, an earning of Rs 5000 per m2 per year., A company hired one of its walls for 3, months. How much rent did it pay?, , Ans. Let sides of triangular flyover are a =, 122m. b = 22m and c = 120 m, a + b + c 122 + 122 + 120, s =, =, 2, 2, 264, = = 132 m, 2, s =132 m, Area of wall =, , 3., , = s ( s − a )( s − b )( s − c ), =, , 12 × 11× 10 × 11× 10 × 12, , =, , 12 × 12 × 11× 11× 10 × 10, = 12 × 11× 10, , =, , = 1320 m 2, Rent for12 months1m 2 = 5000, 5000, Rent for1month1m 2 =, Rs, 12, Rent for 3months1320 m 2, , 16 (16 − 15 )(16 − 11)(16 − 6 ), 16 × 1× 5 × 10, , =, , 4× 4× 5× 5× 2, , =, , = 4×5 2, , s ( s − a )( s − b )( s − c ), , 132 × 10 × 110 × 12, , =, , There is a slide in a park. One of its side, walls has been painted in some colour, with message “Keep the park green, and clean”. If the sides of the wall are, 15m,11m and 6m, find the area painted, in colour., , Ans. Sides of colored triangular wall are 15m,, 11m and 6m, a = 15m, b = 11m & c = 6m., a + b + c 15 + 11 + 6 32, =, s, =, = = 16 m, 2, 2, 2, Area of triangular wall, , = 20 2m 2, , 132 (132 − 122 )(132 − 22 )(132 − 120 ), , =, , 12 × 11× 10 × 11× 10 × 12, , =, , 3a 2, 4, , 3a = 180, 180, a = 60 cm, =, 3, Area of signal board =, , 132 × 10 × 110 × 12, , =, , Hence area painted = 20 2m 2, 4., , Find the area of a triangle two sides, of which are 18cm and 10cm and the, perimeter is 42 cm., Ans. a = 18cm, b = 10 cm, c = ? and perimeter =, 42 cm, Perimeter = a + b + c, 42 = 18 + 10 + c

Page 88 :
137, IX Standard – Mathematics, , Chapter 12 – Heron’s Formula, , 86, , Find the area of the triangle., Ans. Perimeter of an isosceles triangle = 30 cm, Let equal sides be a = 12 cm & other side, b=?, Perimeter = a + a + b, 30 = 12 + 12 + 6, b = 30 – 24 = 6cm, a + b + c 12 + 12 + 6 30, =, =, = = 15cm, s, 2, 2, 2, , =, , s ( s − a )( s − b )( s − c ), , =, , 21( 21 − 18 )( 21 − 10 )( 21 − 14 ), , Area =, , =, , 7 × 3 × 11× 7 × 3, , =, , = 7 × 3 11, = 21 11 cm, , 540, = 10, 54, a = 12x = 12 × 10 = 120cm, b = 17x = 17 × 10 = 170cm, c = 25x = 25 × 10 = 250cm, a + b + c 120 + 170 + 250, =, s =, 2, 2, 540, = = 270cm, 2, =, x, , =, 3× 3 3× 5, = 9 15 cm 2, Exercise 12.2, 8.2, , 1., , Ans., , A park, in the shape of a quadrilateral, ABCD, has C = 90o , AB = 9m, BC =, 12m, CD = 5m and AD = 8m. How much, area does it occupy?, B, , A, D, , o, , In DBCD C =, 90,  Pythogorous , 2, BD, BC 2 + CD 2 , =, ,  theorem, , , 270 ( 270 − 120 )( 270 − 170 )( 270 − 250 ), , =, , (12 ), , 2, , + ( 5), , 2, , BD 2 = 144 + 25 = 169, BD = 13cm, = 9 × 3 × 10 × 10 × 10 × 10 × 5 × 3 × 5 × 2 × 2, = 3 × 3 × 10 × 10 × 5 × 2, In DBDA, a =, 9m, b =, 8m & c =, 13m, 2, =, 9 × 1000 =, 9000cm, a + b + c 9 + 8 + 13, s =, =, 2, 2, An isosceles triangle has perimeter 30, 30, cm and each of the equal sides is 12cm., = = 15m, 2, , =, , 6., , 9m, , C 5m, , Area = s ( s − a )( s − b )( s − c ), , 270 × 150 × 100 × 20, , 3× 5× 3× 3× 3× 3, , 12m, , Sides of a triangle are the ratio of 12 : 17, : 25 and its perimeter is 540 cm. Find its, area., Ans. Let the sides of a triangle are in the ratio, 12 : 17 : 25 then 12x, 17x , 25x, Perimeter = 540m, Perimeter = a + b + c, 540 = 12x + 17x + 25x, 540 = 54x, , =, , 15 × 3 × 3 × 9, , =, , 5., , =, , (15 (15 − 12 )(15 − 12 )(15 − 6 ) ), , =, 2, , s ( s − a )( s − b )( s − c ), , 8m, , c = 42 – 28, c = 14 cm, a + b + c 18 + 10 + 14, =, s =, 2, 2, 42, = = 21cm, 2, Area of triangle using Heron 's formula, , 27 × 10 × 10 × 15 × 10 × 10 × 10 × 2, , Area of DABD =, =, =, , s ( s − a )( s − b )( s − c ), , 15 (15 − 9 )(15 − 8 )(15 − 13), 15 × 6 × 7 × 2

Page 89 :
In DBDA, a =, 9m, b =, 8m & c =, 13m, a + b + c 9 + 8 + 13, s =, =, 2, 2, Chapter, 308 – Heron’s Formula, 138, = = 15m, 2, Area of DABD =, , 6 ( 6 − 3)( 6 − 4 )( 6 − 5 ), , =, , 6 × 3 × 2 ×1, IX Standard – Mathematics, 87, 2 × 3× 3× 2, , For DADC a = 5cm, b = 4cm, & c = 5cm, a + b + c 5 + 4 + 5 14, s, =, =, = = 7 cm, 2, 2, 2, Area of DADC, , 5× 3× 3× 2 × 7 × 2, , =, , =, , = 2 × 3 = 6 cm 2, , s ( s − a )( s − b )( s − c ), , 15 × 6 × 7 × 2, , =, , s ( s − a )( s − b )( s − c ), , =, , 15 (15 − 9 )(15 − 8 )(15 − 13), , =, , =, , 3× 2 5× 7, =, , =, , s ( s − a )( s − b )( s − c ), , =, , 7 ( 7 − 5 )( 7 − 4 )( 7 − 5 ), , =, , 7 × 2 × 3× 2, , = 6 35 m 2, 1 bh, Area of right angle DBCD =, 2, = 1 × 5 × 12, 2, = 30 m 2, ∴ Area of quadrilateral, = Area of DBCD + area of DABD, , = 2 21 cm2, Area of quadrilateral, = area of DABC, + area of DADC, 2, , = 6 cm + 2 21 cm 2, = 6 + 2 × 4.6, = 6 + 9.2, , = 30 + 6 35, = 30 + 6 × 5.92, = 30 + 35.52, , = 15.2 cm 2, , = 65.52 cm 2, 2., Ans., , Find the area of a quadrilateral ABCD, in which AB = 3 cm, BC = 4 cm, CD = 4, cm, DA = 5 cm and AC = 5 cm., , 3., , Radha made a picture of an aeroplane, with coloured paper as shown in Fig, 12.15., 8.15 Find the total area of the paper, used., , D, 4cm, 5cm, , C, 5cm, , 4cm, , A, 3cm, B, In DABC , a = 3cm, b = 4cm & c = 5cm, a + b + c 3 + 4 + 5 12, s, =, =, = = 6 cm, 2, 2, 2, Area of DABC, =, , s ( s − a )( s − b )( s − c ), , =, , 6 ( 6 − 3)( 6 − 4 )( 6 − 5 ), , =, , 6 × 3 × 2 ×1, , =, , 2 × 3× 3× 2, = 2 × 3 = 6 cm 2, For DADC a = 5cm, b = 4cm, & c = 5cm, , Ans. Area of triangular part I, a + b + c 5 + 5 + 1 11, =, =, = = 5.5cm, s, 2, 2, 2, Area =, , s ( s − a )( s − b )( s − c ), , 5.5 ( 5.5 − 5 )( 5.5 − 5 )( 5.5 − 1), , =, =, , 5.5 × 0.5 × 0.5 × 4.5, =, , 11× 0.5 × 0.5 × 0.5 × 0.5 × 9, , = 0.5 × 0.5 × 3 11

Page 90 :
c 5 + 5 + 1 11, a + b + c 5 + 5 + 1=, 11a + b + =, = = 5.5cm, =, =, =s = 5.5cm, s, 2, 2 Formula, 2, 2, 2, 2, IX Standard – Mathematics, 88, Chapter, 12, –, Heron’s, Chapter 12 – Heron’s Formula, 139, Area, =, s, s, −, a, s, −, b, s, −, c, (, )(, )(, ), Area = s ( s − a )( s − b )( s − c ), A triangle and, a parallelogra, 4., A− 1triangle, and 4.a parallelogram, have, 5.5−(15.5, ), = 5.5 ( 5.5 − 5 )( 5.5 −=5 )( 5.5, ) − 5)( 5.5 − 5)( 5.5the, the, same, base, and, same base and, area. If the same, the, sides, of, the 28, triangle are 26, the sides of the triangle are 26 cm,, = 5.5 × 0.5 × 0.5 × 4.5 = 5.5 × 0.5 × 0.5 × 4.5, cm, and, 30, cm,, and, cm and 30 cm, and the parallelogram the parall, = 11× 0.5 × 0.5 × 0.5 × =0.5 11, × 9× 0.5 × 0.5 × 0.5 × 0.5 × 9, onthe, theheight, base 28 cm, find th, stands on the base 28 stands, cm, find, =, 0.5, ×, 0.5, ×, 3, 11, of, the, parallelogram., = 0.5 × 0.5 × 3 11, of the parallelogram., Ans., Ans., 11 0.75 × 3.31, = 0.75 =, 11 0.75 × =, 3.31 0.75 =, C, D, C E, D, 2, of triangular, part I = 2.4825cm 2, Area of triangular part Area, I = 2.4825cm, of part II = Area of rectangle, Area of part II = Area ofArea, rectangle, 30cm, 30cm, 2, 26cm, = l × b = 65 × 1 = 65cm 2= l × b = 65 × 1 = 65cm, 2, Area of part II = 65cm 2Area of part II = 65cm, A, B, A, Area, of part III = Area of trapezium, B 28cm, 28cm, Area of part III = Area of, trapezium, =, =, =, a, 26cm,, b, 28cm, &, c, 30, cm, o, =, =, =, a, 26cm,, b, 28cm, &, c, 30, cm, In Right, In Right angle triangle AED, E =angle, 90o triangle AED E = 90, + b + c 26 + 28 + 30, a + b + c 26 + 28 +s 30a=, 2, 2, s = =, AD, AE 2 + DE 2 =, =, =, AD, AE 2 + DE 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 84, 1, AE, 0.5, =, +, (), ( ), 84, 1) AE + ( 0.5 ), (=, = = 42 cm, = = 42 cm, 2, 2, 2, 2, AE =, 1 − 0.25 =, 0.75cm, AE =, 1 − 0.25 =, 0.75cm, Area, of triangle, Area of triangle, 75 3, 2, 75 3, 2, AE, =, =, = =, AE, = s ( s − a )( s − b )( s − c= ) s ( s − a )( s − b )( s − c ), 100 4, 100 4, 3, 3, = )( 42 (−42, 30−) 26 )( 42 − 28 )( 42 − 30, = 42 ( 42 − 26 )( 42 − 28, cm, Height, trapezium = AE =, AE = of a cm, 2, 2, = 42 × 16 × 14 × 12 = 42 × 16 × 14 × 12, = 1 (a + b) × h, Area of trapezium, a +of, b ) trapezium, = 1 Area, ×h, (, 2, 2, = 7 × 6 × 16 × 7 × 6 × 2= 7 × 6 × 16 × 7 × 6 × 2, 3, 3, 1, = 7×6× 2× 4, 2 + 1) ×, =, = 7×6× 2× 4, = 1 ( 2 + 1) ×, 2(, 2, 2, 2, = 336 cm 2, = 336 cm 2, 3, 3, 3, 1.732, ×, 2, 3 3 3 × 1.732 = =2, 1.299, = Area, = Area of tr, = =, = 1.299 cm, ofcm, parallelogram =Area, Areaofofparallelogram, traingle, 4, 4, 4, 4, b × hof parallelogram= b × h, 2 Area of parallelogram= Area, Area of part III = 1.299Area, cm 2 of part III = 1.299 cm, 336, = 28 × h, 336, = 28 × h, Area of IV & V part Area of IV & V part, 336, 336, h=, = 12 cm, = Area of 2 right angle triangle, h=, = 12 cm, = Area of 2 right angle triangle, 28, 28, = 2× 1 × b× h, = 2× 1 × b× h, height =12 cm, height =12 cm, 2, 2, =2 × 1 × 1.5 × 6, =2 × 1 × 1.5 × 6, 5. field, A rhombus, 2, 5., A rhombus shaped, has greenshaped, grass field has gre, 2, 2, 2, for, 18, cows, to, graze., for, 18, cows, to, graze., If, each, side, of, the If each sid, =, 9, cm, = 9 cm, rhombus, is, 30m, and its longer d, rhombus, is, 30m, and, its, longer, diagonal, Total, Total Area = (Area of part, I +Area = (Area of part I +, is of, 48m,, how, much, is 48m, how much area, grass, field, willarea of grass fi, III, Area of part II + Area ofArea, partof, IIIpart II + Area of parteach, cow be getting? each cow be getting?, +, Area, of, part, IV, +, Area, of, part, V), Ans., + Area of part IV + Area of part V), Ans., =, 2.4825, +, 6.5, +, 1.299, +, 9, = 2.4825 + 6.5 + 1.299 + 9, , = 19.2815, , = 19.2815, = 19.28cm, , 2, , = 19.28cm 2

Page 91 :
89, IX Standard – Mathematics, , Chapter 8 – Heron’s Formula, , 140, , D, 30cm, , 30cm, , A, , C, , 48m, 30cm, , 30cm, , Ans. For one triangular piece a = 20 cm, b = 50, cm and c = 50 cm., a+, 20 +, 50 +, 50, + bb +, + cc 20, + 50, + 50, ss a=, =, =, =, 22, 22, 120, 60 cm, cm, = 120, = 60, =, =, 22, Area, Area of, of one, one triangle, triangle, ==, ==, , B, , a = 30cm, b = 30m & c = 48m, a + b + c 30 + 30 + 48 108, =, s =, =, 2, 2, 2, = 54 m, Area of the triangle, =, , s ( s − a )( s − b )( s − c ), , =, , 54 ( 54 − 30 )( 54 − 30 )( 54 − 48 ), , == 10, 10 ×, 10 ×, × 10, × 22 66, 2, =, 200 66 cm, cm 2, = 200, Area of, of five, five triangles, triangles of, of one, one colour, colour, ∴, ∴ Area, , (, , 2, =, 1000 66 cm, cm 2, = 1000, 2, Hence1000, Hence1000 66 cm, cm 2 of, of each, each colour, colour is, is, requi, red, for, the, umbrella., required for the umbrella., , 7., , = 2 × 432, = 864 m 2, Area of grass for18cows = 864 m 2, 864, Area of grass for each cow =, 18, 2, = 48 m, , An umbrella is made by stitching, 10 triangular pieces of cloth of two, different colours, each piece measuring, 20cm, 50cm and 50cm. How much, cloth of each colour is required for the, umbrella?, , ), , 2, =, 200 66 cm, cm 2, = 55 200, , 9 × 6 × 24 × 24 × 6, = 3 × 6 × 24, = 18 × 24, , 6., , 60, 60 (( 60, 60 −, 50 )(, 60 −, 50 )(, 60 −, 20 )), − 50, − 50, − 20, )( 60, )( 60, 60, 60 ×, 10 ×, 10 ×, 40, × 10, × 10, × 40, 10, 10, 10, 6, ×, ×, ×, 10 × 10 × 10 × 6 ×, 10 ×, × 10, × 44, , ==, ==, , =, , Area of triangle = 432 m 2, Area of rhombus= 2 × Area of triangle, , ss (( ss −, − aa )(, )( ss −− bb )(, )( ss −− cc )), , Ans., , A kite in the shape of a square with a, diagonal 32 cm and an isosceles triangle, of base 8cm and sides 6cm each is to be, made of three different shades as shown, in Fig 12.17. How much paper of each, shade has been used in it?

Page 92 :
90 12 – Heron’s Formula, Chapter, , IX Standard – Mathematics, 141, of the triangle being 9 cm, 28 cm and 35, cm. Find the cost of polishing the tiles at, the rate of 50p per cm2., , A, , D, , B, , 6cm, , C, , 6cm, , 8cm, In a square ABCD side = a & diagonal =, 32 cm, In DABD A =, 90o, 2, =, BD, AB2 + AD 2, , ( 32 )=, 2, , a2 + a2, , Ans. For one triangular tile a=9 cm, b = 28 cm, and c=35 cm, a + b + c 9 + 28 + 35 72, s, =, =, = = 36 cm, 2, 2, 2, Area of one triangular tile, , 2, 2a=, 32 × 32, 32 × 32, a2 =, 2, 2, a = 512 cm 2, Area of shade I = Area of shade II, 512, = = 256 cm 2, 2, Area of part I + Area of part II =, 512 cm 2, , =, , s ( s − a )( s − b )( s − c ), , =, , 10 (10 − 8 )(10 − 6 )(10 − 6 ), , =, , 36 × 27 × 8 × 1, , =, , 36 × 9 × 3 × 4 × 2, = 6 × 3× 2 3× 2, = 36 6 cm 2, Area of 16 tiles, = 16 × 36 6, , = 576 6 cm 2, polishing, the the, tilestiles, at the, rate, Cost of tile, polishing, at the, rate, 50P per cm 2, 576 × 6 × 50, 100, = 288 6, = 288 × 2.44, = 705.6 Rs, =, , 10 × 2 × 4 × 4, , =, , = 4× 2 5, = 8 5 cm 2, = 8 × 2.236, , 9., , = 17.92 cm 2, , 8., , A floral design on a floor is made up of, 16 tiles which are triangular, the sides, , 36 ( 36 − 9 )( 36 − 28 )( 36 − 35 ), , =, , Area of shaded part III = Area of scaleneD le, a + b + c 6 + 6 + 8 20, s, =, =, = = 10 cm, 2, 2, 2, Area of triangle, =, , s ( s − a )( s − b )( s − c ), , Ans., , A field is in the shape of a trapezium, whose parallel sides are 25m and 10m., The non - parallel sides are 14m and, 13m. Find the area of the field.

Page 93 :
91, IX Standard – Mathematics, , Chapter 8 – Heron’s Formula, , 142, , 10m, , D, 14m, , A, , Additional Problems, , C, , 13m, , F, E, 15m, , 13m, , s ( s − a )( s − b )( s − c ), , =, , 21( 21 − 14 )( 21 − 15 )( 21 − 13), , Multiple Choice Questions, , 1., , Area of a triangle, a) 1/2 x base x height, b) Base x height, c) 1/3 x base x height, d) 1/4 x base x height, , 2., , Area of an equilateral triangle of side a, is, 3a, 3, a), b), a c) 3a 2 d) a 3, 2, 4, , 3., , Area of a parallelogram, a) 1/2 x base x height, b) base x height, c) 1/4 x base x height, d) 1/3 x base x height, , 4., , The area of a right triangle is 36m2 and, its base is 9cm. Find the length of the, perpendicular., a) 32 cm, b) 4cm, c) 16 cm, d) 8 cm, , 5., , The side of an equilateral triangle is, 6cm. The area of the triangle is, a) 6 3 cm 2, b)16 3 cm, , B, , 25m, In a trapezium ABCD with AB = 25 m, CD, = 10 m, BC = 13m & AD = 14 m. From D,, draw DE || BC, DE = BC = 13m and BE = DC = 10m, In triangle ADE a = 14cm, b 13m & c =, 15m, a + b + c 14 + 13 + 15 42, =, s =, = = 21m, 2, 2, 2, Area of triangle ADE, =, , I., , 21× 7 × 6 × 8, , =, , 7 × 3× 7 × 4 × 2 × 3× 2, = 7 × 3× 2 × 2, , =, , = 84m 2, Area of triangle= 1 × b × h, 2, 1, × 13, 84 =, 15× h, 2, 84 × 2 56, =, h =, cm, 15, 5, Area of parallelogram= b × h, 56, = 10 ×, 5, = 2 × 56, , c 9 3 cm 2, d), 6., , The side of a square is 5cm. Its perimeter, is, a) 5 cm, b) 25cm c) 20 cm d) 10 cm, , 7., , The diagonals of a rhombus are 10 cm, and 8cm. Its area is, a) 80cm2, b) 40cm2, 2, c)9cm, d) 36cm2, , 8., , 1 hectare is, a) 10000 m2, c) 100m, , 9., , The area of a square is 625m2, then its, perimeter is, a) 250m, b) 500m, c) 100m, d) 250m, , = 112 cm 2, Area of the field = Area f AED + Area of, Parallelogram, = 84 + 112, = 196 m 2, , d) 3 3 m 2, , b) 500m, d) 250m

Page 94 :
92 12 – Heron’s Formula, Chapter, 10., , 143, , A regular hexagon has a side 8cm. Find, its area, a)8 3 cm 2, b) 96 3 cm 2, c) 4 3 cm 2, , 11., , IX Standard – Mathematics, Perimeter, 4, 146, = = 36.5cm, 4, =, , d)12 3 cm 2, , A, , Find the semi-perimeter of the triangle, whose sides are 21cm, 20cm and 29 cm, a) 35 cm, b) 70 cm, c) 41 cm, d) 50 cm, , 36.5 cm, mm, 5cc, , 55..5, , 36.5cm, , A, D, 36.5cm, , A 36.5cm A, B, C, The diagonals of rhombus are 210cm and, For DABC, 8cm. Its area is, =, a 36.5,, =, b 36.5,, =, c 55cm, a) 80cm2 b) 40cm2 c) 9cm2 d) 36cm2, a + b + c 36.5 + 36.5 + 55 128, =, s =, = = 64cm, Ans. 1) a, 2) b, 3) b, 2, 2, 2, 4) d, 5) c, 6) c, ∴ Area of DABC, 7) b, 8) a, 9) c, = s ( s − a )( s − b )( s − c ), 10) b, 11) a, 12) ba, 12., , = 64 ( 64 − 36.5 )( 64 − 36.5 )( 64 − 55 ), , II. Answer the following questions, , 1., Ans., , A rectangular hexagon has a side 8cm., Determine its perimeter and area., E, F, , D, 0, , C, , A, B, Side = 8 cm, Perimeter = 6 x 8 = 48 cm, Area of equilateral triangle OAB, 3, 2, =, ( side ), 4, 3 2, = =, (8) 16 3 cm 2, 4, Area of regular hexagon, = 6 × Area of equilateral triangle OAB, = 6 × 16 3, , = 660cm 2, Area of the rhombus ABCD, = 2Area of DABC, = 2 × 660, = 1320 cm 2, 1 d d = 1320, 2 1 2, 1 ( 55 ) d = 1320, 2, 2, 1320 × 2, d2 =, 55, d 2 = 48cm, 3., , In the following figure, caculate the, area of the shaded portion., P, 52c, , m, , c, 12, , = 96 3 cm 2, , 64 × 27.5 × 9 × 27.5, =, 8 × 27.5 × 3, , =, , R, , 16, , The perimeter of a rhombus is 146 cm., One of its diagonals is 55cm. Find the, length of the other diagonal and area of, the rhombus., Ans. Length of a side of the rhombus, , cm, , m, , 2., , m, , 48c, , Q, Ans. In right triangle PSQ

Page 95 :
144 8 – Heron’s Formula, Chapter, 2, PQ, =, PS2 + QS2, , (12 ), , =, , 2, , + (16 ), , 2, , = 144 + 256 = 400, =, PQ, , =, 400 20 cm, , Now, For DPQR a= 20 cm, b= 48cm, & c = 52 cm, =, ∴s, , a + b + c 20 + 48 + 52, =, 2, 2, , 120, = 60cm, 2, ∴ Area of DPQR, , =, , = s ( s − a )( s − b )( s − c ), =, , 60 ( 60 − 20 )( 60 − 48 )( 60 − 52 ), 60 × 40 × 12 × 8, , =, , 10 × 3 × 10 × 4 × 4 × 3 × 4 × 2 × 2, = 10 × 3 × 4 × 2 × 2, , =, , = 480 cm 2, Area of DPSQ =1 × base × altitude, 2, 1, =, × 16 × 12, 2, = 96 cm 2, ∴ Area of shaded portion, = Area of DPQR − area of DPSQ, = 480 − 96 = 384 cm 2, , IX Standard – Mathematics, 93

Page 96 :
94, , 31, , CHAPTER -- 39, CHAPTER, , Coordinate Geometry, Geometry, Coordinate, Key Points :, , ●, ●, ●, , Two perpendicular number lines intersecting at point zero are called co-ordinate axes., Rectangular coordinate system has been named as ‘Cartesian System’., The horizontal number line is the x- axis (denoted by XOX1) and the vertical number line is, the y-axis denoted by (YOY1)., y, y-axis, 5, 4, , Quadrant II, (–, +), , Quadrant I, (+, +), , 3, 2, 1, , x, , 1, , –5, , –4, , –3, , –2, , 0, , –1, , x-axis, x, 1, , 2, , 3, , 4, , 5, , –1, –2, , Quadrant III, (–, –), , –3, , Quadrant IV, (+, –), , –4, –5, , ●, ●, ●, ●, ●, ●, , y1, The coordinate axis divide the plane into four parts called quadrants., The point of intersection of x - axis and y - axis is called origin and denoted by ‘0’., The perpendicular distance from y-axis is called the x - coordinate (ABSCISSA) of the point., The perpendicular distance from x - axis is called the y - coordinate (ordinate) of the point., The coordinates of a point p is represented as p(x,y)., Co-ordinates of the origin are (0,0)

Page 97 :
95, IX Standard – Mathematics, IX Standard – Mathematics, , Chapter, 9 – Coordinate Geometry, 32, , 32, , ●, ●●, ●●, ●, , Coordinates of any point on x - axis will be the form (x,0), IX Standard – Mathematics, 32, Coordinates, of any, any point, point on, on y-axis, x - axiswill, willbebeofthe, Coordinates, of, theform, form(x,0), (0,y), Coordinates, of any apoint, on y-axis, willform, be of(+,+), the form, (0,y), The, point, the, the, first quadrant, (– , +) in the second, ● coordinates, Coordinatesof, of any, point are, on xof, - axis, will be the, formin(x,0), The, coordinates, of, a, point, are, of, the, form, (+,+), in, the, first quadrant,, , +) in the, second, quadrant, (–,–) in the, third, quadrant, fourth, where(–+ denotes, a positive, ●, Coordinates, of any, point, on y-axisand, will(+,–), be of in, thethe, form, (0,y) quadrant, quadrant, (–,–), in, the, third, quadrant, and, (+,–), in, the, fourth, quadrant, where, +, denotes, a, positive, The coordinates, of a point, are of the, form, (+,+) in the first quadrant, (– , +) in the second, real● number, and – denotes, a negative, real, number., (–,–), in(y,x), the third, (+,–), – ≠denotes, a quadrant, negative, real, number., ●, Ifreal, x ≠number, y,quadrant, then and, (x,y), and, (x,y) =and, (y,x), if in, x the, = y.fourth quadrant where + denotes a positive, number, denotes, negative, real number., ●, If x ≠ y,real, then, (x,y)and, ≠ –(y,x), anda (x,y), = (y,x), if x = y., ●32 If x ≠ y, then (x,y) ≠ (y,x) and (x,y) = (y,x) if x = y., IX Standard – Mathematics, Exercise, 3.1, 9.1, Exercise, 3.1, Exercise 3.1, , ●, Coordinates of any point on x - axis will be the form (x,0), 1., How, will, you describe the position of a table lamp on your study table to another person?, ●, Coordinates, of any point, on y-axis will, betable, of thelamp, form (0,y), 1. Consider, How, you, describe, position, of, on, your, study, table, to another, person?, 1. will, How, will, you describe, the, position, of aaas, table, lamp onChoose, your, study, table, to another, person?edges, Ans., the, lamp, asofaathe, point, andoftable, a(+,+), plane., any, two, of, ●, The coordinates, point are, the form, in the first quadrant,, (– perpendicular, , +) in the second, Ans., Consider, the, lamp, as, a, point, and, table, as, a, plane., Choose, any any, two, perpendicular, edges of, Ans. the, Consider, the, lamp, as, a, point, and, table, as, a, plane., Choose, two, perpendicular, edges, of, table., Measure, the, distance, of, the, lamp, from, shorter, edge., Suppose, it, is, 40cm, and, again, quadrant, (–,–), in thethe, third, quadrant, andlamp, (+,–)from, in theshorter, fourth edge., quadrant, whereit+isdenotes, a positive, the table., Measure, distance, ofthe, the, Suppose, 40cm, and, again, the table., Measure, the, distance, ofedge,, lamp, from shorter, edge., Suppose, it, islamp, 40cm, and again, measure, the, distance, from, longer, and, suppose, 65cm., You, can, write, the, position, as, real, number, and, –, denotes, a, negative, real, number., measure the distance from longer edge, and suppose 65cm. You can write the lamp position as, measure, from, longer, andifsuppose, 65cm. You can write the lamp position as, ●, If(40,65), xthe, ≠ y,distance, then, ≠ (y,x), and (x,y), =, xfix., = y., (40,65), (or), (65,40), depending, onedge,, order, (or) (x,y), (65,40), depending, onthe, the(y,x), order, fix., (40,65) (or) (65,40) depending on the order fix., Exercise 3.1, , 1., How will you describe the position of a table lamp on your study table to another person?, Ans. Consider the lamp as a point and table, as a plane. Choose any two perpendicular edges of, 40cm, the table. Measure the distance of the40cm, lamp from shorter edge. Suppose it is 40cm and again, measure the distance from longer edge,40cm, and suppose 65cm. You can write the lamp position as, (40,65) (or) (65,40) depending on the order fix., 65cm, , 65cm, 65cm, 40cm, , w, , Street 5, , Street, Street, 5 5, , Street 5, , Street 4, , Street, Street, 4 4, , Street 4, , Street 3 Street, Street, 3 3 Street 3, , Street, Street, 1 1, , Street 1, , Street, 2 2 Street 2, Street 2 Street, , All2.the (Street, other Plan), streets, the, to these, roads, andatare, 200mofapart., There are, : Aof, city, hascity, tworun, mainparallel, roads which, cross each, other, the centre, the city., 5 streetsThese, in each, direction., Using, 1cm, =, 200m,, draw, a, model, of, the, city, on, your, notebook., two roads are along the North-South direction and East-South direction and Eastdirection., the, single, lines.which cross each other at the centre of the city., 2. Represent, (Street West, Plan), : roads/streets, A city has twobymain, roads, Ans. are many cross - streets in your model.65cm, There, Across, particular, cross at, - street, is made, by, two, 2. These, (Streettwo, Plan), : Aare, cityalong, has two, roads which, each, other, the, centre, of, the, city., roads, the main, North-South, direction, and, East-South, direction, and, East1, N, streets,, one, running, in, the, North, South, direction, and, another, in, the, East, West, direction., Thesedirection., two roads are along the North-South direction and East-South direction and EastWest, street is referred to in the following manner : If the 2nd street running in the, West cross, direction., Ans. Each, Ans. North - South direction1 and 5th in the East - West direction meet at some crossing, then we, N has(2,, 2. call, (Street, city, two, roads, which, cross eachfind, other: atStreet, the centre, of the city., 5, will, this Plan), cross: -Astreet, 5).main, Using, this, convention,, (2,5), N1 along the North-South, These two roads are, direction and East-South direction and EastStreet 4, (i) How many cross - streets, can be referred, to, as, (4,, 3), (3,4), West direction., Street 3, (ii)Ans., How many cross - streets can be referred to as (3, 4), (4,3), Street 2, Ans., Street 5, N1, (2,5), StreetStreet, 1, Street 45, (2,5) (3,4), EStreet 4, w, Street 3, (3,4), (4,3), Street, StreetStreet, 5, 23, (2,5), (4,3), StreetStreet, 4, (3,4), Street 12, Both the cross - streets are marked in the figure given. They are uniquelyStreet, found3 because of the, Street 1, two reference lines we have used for locating them. (4,3), Street 2 E, w, w, Street 1 E, Street 1, , 2., , E, , Both the cross - streets are marked in the figure given. They are uniquely found because of the, Bothreference, the crosslines, - streets, are marked, the figure, given. They are uniquely found because of the, two, we have, used forinlocating, them., Both the cross, streets, are used, marked, the figurethem., given. They are uniquely found because of the, two reference, lines- we, have, forinlocating, two reference lines we have used for locating them.

Page 98 :
96, Chapter, 3 – Coordinate Geometry, , IX Standard – Mathematics, , 33, , Exercise 9.2, 3.2, , 1., , Write the answer of each of the following questions :, i. What is the name of horizontal and the vertical lines drawn to determine the position, of any point in the Cartesian plane?, ii. What is the name of each part of the plane where these lines intersect., iii. Write the name of the point where these two lines intersect., Ans. i. Horizontal line is called x-axis and vertical line is called y-axis., ii. Quadrants., iii. The point where these two lines interest is called origin., 2., , See Fig 93.14, and write the following :, i. The coordinates of B., ii. The coordinates of C., iii. The point identified by the coordinates (–3,–5), iv. The point identified by the coordinates (2,–4), v. The abscissa of the point D., vi. The ordinate of the point H., vii. The coordinates of the point L., viii. The coordinates of the point M., Y1, , L, , 5, 4, 3, B, , D, , 2, 1, M, , X1, –5, , –4, , –3, , –2, , 0, , –1, , 1, , 2, , 3, , 4, , 5, , 6, , –1, –2, –3, , H, , –4, E, , Ans. i. Coordinates of, f B → (–5,2), iii. Point E, v. Abscissa of point D, x = 6, vii. Coordinates of L → (0,5), , G, , –5, , C, Y, , ii. Coordinates of C → (5,–5), iv. Point G, vi. Ordinate of point H y = –3, viii. Coordinates of M → (–3,, (3,0)0), , X

Page 99 :
97, IX Standard – Mathematics, , Chapter, 9 – Coordinate Geometry, 34, Exercise 9.3, 3.3, , 1., , In which quadrant or on what axis do each of the points (–2,4), (3,–1),(–1,0),(1,2) and, (–3,–5) lie? Verify your answer by locating them on the Cartesian plane., Ans. The point (–2,4) lies in the II quadrant., The point (3, –1) lies in the IV quadrant, The point (–1,0) lies on the negative x-axis., The point (1,2) lies on the I Quadrant., The point (–3,–5) on III quadrant., y, , 5, (–2,4), , 4, 3, 2, , (1,2), , 1, (–1,0), , x1, –5, , –4, , –3, , –2, , 0, , –1, –1, , x, 1, , 2, , 3, , 4, , 5, , (3,–1), , –2, –3, –4, , (–3,–5), , –5, y1, , 2., , Ans., , Plot the points (x,y) given in the following table on the plane, choosing suitable units of, distance on the axes., x, y, , -2 -1, 0, 8 7 -1.25, , 1, 3, , 3, -1

Page 100 :
98 3 – Coordinate Geometry, Chapter, , IX Standard – Mathematics, , 35, , y1, 8, , (–2,8), , 7, , (–1,7), , 6, 5, 4, 3, , (1,3), , 2, 1, (–1,0), , x1, –5, , –4, , –3, , –2, , 0, , –1, –1, , x, 1, , 2, , (0,1.25), , –2, y, Additional Problems, , I., 1., , Multiple Choice Questions, The coordinates of the origin are, a) (1,1), b) (0,1), c) (1,0), , d) (0,0), , 2., , The vertical line is called, a) y - axis b) origin, , c) x - axis, , d) quadrant, , 3., , The horizontal line is called, a) y - axis b) origin, c) x - axis, , d) quadrant, , 4., , The point of intersection of the coordinate axes is called, a) x - axis b) y - axis, c) origin, d) quadrant, , 5., , For a point on x - axis, y is equal to, a) 0, b) 1, c) –1, , d) none of these, , 3, (3,–1), , 4, , 5

Page 101 :
99, IX Standard – Mathematics, , Chapter 9 – Coordinate Geometry, , 36, , 6., , The coordinate axis divide the plane into how many parts., a) 1, b) 2, c) 3, d) 4, , 7., , If x is negative and y is positive, then the point (x,y) lies in, a) I quadrant, b) IIIrd quadrant c) IVth quadrant d) IInd quadrant, , 8., , The value (2,-3) lies in, a) I quadrant, b) II quadrant, , c) III quadrant, , d) IV quadrant, , 9., , The value (0,5) lies in, a) x - axis, b) y - axis, , c) II quadrant, , d) IV quadrant, , c) I quadrant, 5. a, 6. d, , d) IInd quadrant, 7. d, 8. d, 9. b, , 10., , The value of (–3,0) lies in, a) x-axis, b) y - axis, Ans. 1. d, 2. a, 3. c, 4. c, , Answer the following Questions, , 1., Represent given points A(2,3), B(0,5), C(5,0), D(5,4), E(–2,3) and F(–3,–5), Ans., y, +5, , E(-2,3), , B(0,5), , +4, +3, , A(2,3), , D(5,4), , +2, +1, , x, , 1, , –5 –4 –3 –2 –1, -1, , C(5,0), 0 1 2 3 4 5 6, , x, , -2, -3, -4, , F(–3,–5), , 2., , Ans., , -5, , y, , Plot the points of (x,y) gievn in the, teh following table, x, y, , –1, 3, , 2, 3, , 0, –4, , –3, –2, –4, –5, , –2, –3, , y, +5, , (-1,3), , +4, +3, , (2,3), , +2, +1, , x1, , –5 –4 –3 –2 –1, -1, , (–2,–3), (–3,–5), , 0 1 2 3 4 5 6, , -2, -3, -4, -5, , (0,-4), , y, , x, , 10. a

Page 102 :
100, , CHAPTER - 10, , Linear Equations in Two Variables, Key Points :, , ●●, ●●, ●●, ●●, ●●, ●●, ●●, ●●, ●●, ●●, , Equation : A statement that a non constant algebraic expression is equal to zero., Linear equation : An equation of degree of a variable is one., An equation of the form ax + bx + c = 0. Where a,b and c are real numbers, such that a and b, are not both zero, is called a linear equation in two variables., A linear equation in two variables has infinitely many solutions., A graph of every linear equation in two variables is a straight line., x = 0 is the equation of the y - axis and y = 0 is the equation of x - axis., The graph of x = a is a straight line parallel to the y - axis., The graph of y = a is a straight line parallel to the x-axis., An equation of the type y = mx represents a line passing through the origin., Every point on the graph of a linear equation in two variables is a solution of the linear equation., Moreover, every solution of the linear equation is a point on the graph of the linear equation., , Exercise 10.1, , 1., , The cost of a notebook is twice the cost, of a pen. Write a linear equation in two, variables to represent this statement., (Take the cost of a notebook to be Rs x, and that of a pen to be Rs. y), Ans. Let the cost of a note book to be Rs x and, the cost of a pen to be Rs y. Then, according, to the given condition of the question., x = 2y, x – 2y = 0, It is the required linear equation in two, variable x and y., 2., , Express the following linear equations, in the form ax + by + c = 0 and indicate, the values of a,b and c in each case :, –, i., 2x + 3y = 9.35, –, Ans. 2x + 3y = 9.35, –, 2x + 3y – 9.35 = 0, Comparing with ax + by + c = 0, we get, –, a = 2, b = 3 and c = –9.35, , ii., , x−, , y, − 10 =, 0, 5, , Ans. It is in the form of ax + by + c = 0, a = 1, b = -1/5 & c = –10., iii. –2x + 3y = 6, Ans. –2x + 3y – 6 = 0, It is in the form of ax + bx + c = 0, a = –2, b = 3 and c = –6, iv. x = 3y, Ans. x – 3y = 0, It is in the form of ax + by + c = 0, a = 1, b = -3 and c = 0, v., 2x = –5y, Ans. 2x + 5y + 0 = 0, It is in the form of ax + by + c = 0, a = 2, b = 5 and c = 0, vi. 3x + 2 = 0, Ans. 3x + 0y + 2 = 0, It is in the form of ax + by + c = 0, a = 3, b = 0 & c = 2

Page 103 :
Chapter 10 – Linear Equations in Two Variables, vii. y – 2 = 0, Ans. 0x + y – 2 = 0, It is in the form ax + by + c = 0, a = 0, b = 1 & c = –2, , 0, =, 4, 1, When x= 1, y= =, 4, 2, When x= 2, y= =, 4, 4, When x= 4, y= =, 4, , Exercise 10.2, , Write four solutions for each of the, following equations :, , i., 2x + y = 7, Ans. y = 7 – 2x, When x = 0, y = 7 - 2(0) = 7 - 0 = 7, When x = 1, y = 7 - 2(1) = 7 - 2 = 5, When x = –1, y = 7–2(–1) = 7 + 2 = 9, When x = 2, y = 7 – 2(2) = 7–4 = 5, When x = –2 , y = 7–2(–2) = 7 + 4 = 11, \Four solutions are (0,7)(1,5)(–1,9) and, (2,5), ii. px + y = 9, Ans. y = 9 – px, When x = 0, y = 9 – p(0) = 9, When x = 1, y = 9 – p(1) = 9 – p, When x = 2, y = 9 – p(2) = 9 – 2p, When x = 2p, y = 9 – p x 2/p = 9 – 2 = 7, \Four solutions are, 2, ( 0,9 )(1,9, −p )( 2,9 − 2p ) and  , 7 , p , iii. x = 4y, Ans., x, y=, 4, , 0, = 0, 4, 1, When x= 1, y= = 1, 4, 4, When x= 0, y=, , 0, 1, , 4, , 1, 2, 1, , (, , \ Four solutions are ( 0, 0 ) , 1, 1, , 1., , 2., , 101, , x, 4, , When x= 0, y=, , viii. 5 = 2x, Ans. 2x + 0y – 5 = 0, It is in the form ax + by + c = 0, a = 2, b = 0 and c = –5, Which one of the following options is, true, and why?, y = 3x + 5 has, i. a unique solution, ii. Only two solutions, iii. Infinitely many solutions, Ans. iii. infinity many solution is true., Reason : For every value of x, there is a, corresponding value of y and vice-versa., , y=, , and ( 4,1), 3., , 4, , )( 2, 1 2 ), , Check which of the following are, solutions of the equation x – 2y = 4 and, which are not :, , i., (0,2), Ans. x – 2y = 4, 0 – 2(2) = 4, –4 ≠ 4, LHS ≠ RHS, \(0,2) is not a solution of x – 2y = 4., ii. (2,0), Ans. x – 2y = 4, 2 – 2(0) = 4, 2≠4, LHS ≠ RHS, \(2,0) is not a solution of x – 2y = 4, iii. (4,0), Ans. x – 2y = 4, 4 – 2(0) = 4, 4=4, LHS = RHS, \(4,0) is a solution of x – 2y = 4, iv., , (, , 2, 4 2, , ), , (, , ), , Ans. x – 2y = 4, x 2− 4 2 =, 4, √2 – 2(4√2) = 4, 2 −8 2 =, 4, −7 2 ≠ 4, LHS ≠ RHS, \, , (, , ), , 2, 4 2 is not a solution of x − 2y =, 4

Page 104 :
102, Chapter 4 – Linear Equations in Two Variables, v., (1,1), Ans. x – 2y = 4, 1 – 2(1) = 4, –1 ≠ 4, \(1,1) is not a solution of x – 2y = 4, 4., , Find the value of k, if x = 2, y = 1 is a, solution of the equation 2x + 3y = k., Ans. x = 2 & y = 1, 2x + 3y = k, 2(2) + 3(1) = k, 4+3=k, k=7, Exercise 10.3, 4.3, , 1., , Draw the graph of each of the following, linear equations oin two variables :, , i., x+y=4, Ans. y = 4 – x, x = 0, y = 4 – 0 = 4, x = 1, y = 4 – 1 = 3, x = 2, y = 4 – 2 = 2, x, y, , 0, 4, , 1, 3, , y, , x1 –5 –4 –3 –2 –1, –1, –2, –3, –4, –5, –6, , x, y, , (0,4), (1,3), (2,2), (4,0), , x1, , 1 2 3 4 5, , –1, –2, –3, –4, –5, –6, , x, , x+y=4, , y1, ii. x – y = 2, Ans. y = x – 2, , x 0 1 2, y -2 -1 0, When x = 0, y = (0) – 2 = –2, When x = 1, y = 1 – 2 = –1, When x = 2, y = 2 – 2 = 0, y, 6, 5, 4, 3, 2, 1, (2,0), , x–y=2, , 1 2 3 4 5 x, (1,–1), (0,–2), , y1, , iii. y = 3x, Ans. When x = 0, y = 3(0) = 0, When x = 1, y = 3(1) = 3, When x = –1, y = 3(–1) = –3, , 2, 2, 6, 5, 4, 3, 2, 1, , IX Standard – Mathematics, 39, , 0, 0, , 1, 3, , –1, –3, 6, 5, 4, 3, 2, 1, , x1 –5 –4 –3 –2 –1, –1, –2, (–1,–3) –3, –4, –5, –6, , y, , y = 3x, (1,3), , 1 2 3 4 5 x, , y1

Page 105 :
3y, = ax + 7, 3=, ( 4 ) a ( 3) + 7, = 3a + 7IX Standard – Mathematics, 40, Chapter, 10 – Linear Equations in Two Variables12, 103, 12 − 7 =, 3a, iv. 3 = 2x + y, 3a = 5, Ans. y = 3 – 2x, a=5, When x = 0, y = 3 – 2(0) = 3, 3, When x = 1, y = 3 – 2(1) = 3 – 2 = 1, When x = 2, y = 3 – 2(2) = 3 – 4 = –1, 4., The taxi fare in a city is as follow : For, the first kilometer, the fare is Rs 8 and, x 0 1 2, for the subsequent distance it is Rs 5, y 3 1 -1, per km. Taking the distance covered is, y, x km ad total fare as Rs y, write a linear, equation for this information, and draw, 6, its graph., 5, Ans. Total distance covered = x km, 4, Total fare = Rs y, (0,3), 3, Fare for first kilometer = Rs 8, 2, Subsequent distance = (x – 1)km, (1,1), Fare for subsequent distance = Rs (x –1), 1, According to the condition, x1 –5 –4 –3 –2 –1, 1 2 3 4 5 x, y = 8 + 5(x – 1), –1, (2,–1), y = 8 + 5x – 5, –2, y = 5x + 3, 3 = 2x + y, –3, When x = 0, y = 5(0) + 3 = 3, –4, When x = 1, y = 5(1) + 3 = 8, When x = 2, y = 5(2) + 3 = 13, –5, –6, y1, 2., , Give the equations of two lines passing, through (2,14). How many more such, lines are there, and why?, Ans. The equations of two lines passing through, (2,14) can be taken as (x,y) = (2,14), 2x + y = 18, 14x – 2y = 0, There are infinitely many such lines, because through a point an infinite number, of lines can be drawn., 3., , If the point (3,4) lies on the graph of the, equation 3y = ax + 7, find the value of a., Ans. If a point (x,y) = (3,4) lies on the graph of, the equation 3y = ax + 7, x=3&y=4, 3y, = ax + 7, 3=, ( 4 ) a ( 3) + 7, 12, = 3a + 7, 12 − 7 =, 3a, 3a = 5, a=5, , 3, , x, y, , 0, 3, , 1, 8, , 2, 13, 8, 7, 6, 5, 4, 3, 2, 1, , y, , y = 5x + 3, (1,8), y = 5x + 3, (0,3), , 1 2 3 4 5 x, , x1 –5 –4 –3 –2 –1, –1, –2, –3, –4, –5, –6, y1

Page 106 :
104 4 – Linear Equations in Two Variables, Chapter, 5., , From the choices given below, choose, the equation whose graphs are given in, Fig, 10.6and, andFig, Fig4.7., 10.7, Fig4.6, For, Fig, 10.6, Fig, 10.7, For, Fig, 4.6 For, For, Fig, .4.7, i. y = x, ii. x + y = 0, iii. y = 2x, iv. 2 + 3y = 7x, , i. y = x + 2, ii. y = x – 2, iii. y = –x + 2, iv. x + 2y = 6, , IX Standard – Mathematics, 41, , draw the graph of the same by taking, the constant force as 5 units. Also read, from the graph the work done when the, distance traveled by the body is, i. 2 units, ii. 0 unit, Ans. Let the work done by the constant force, be y units and the distance traveled by the, body be x units and constant force = 5 units., Work done = Force x displacement, y = 5x, x, y, , 0, 0, , 1, 5, 11, 10, 9, 8, 7, 6, 5, 4, 3, 2, 1, , Fig 10.6, 4.6, , x1 –5 –4 –3 –2 –1, –1, –2, –3, y = 5x, –4, , If the work done by a body on, application of a constant force is directly, proportional to the distance traveled, by the body, express this in the form, of an equation in two variables and, , y, B, , (2,10), , (1,5), , (0,0), , A, 1 2 3 4 5 x, , y1, i. Let A → (2,0), through A, draw a line, parallel to oy to intersect the graph of the, equation y = 5x at B. Through B, Draw a, line parallel to ox to intersect oy at c. then, c → (0,10) \ work done when the distance, traveled by the body is 2units = 10 units., ii. Clearly y = 0 when x = 0, so the work, done when the distance traveled by the, body is 0 units., , Fig 10.7, 4.7, Ans. For Fig 10.6, 4.6. The correct equation is ii) x +, y = 0 graph points holds good for equation, x + y = 0., Ans. For Fig 10.7, 4.7. The correct equation is iii), y = –x + 2 graph points holds good for, equation y = –x + 2, 6., , 2, 10, , 7., , Yamini and Fatima, two students of, Class IX of a school, together contributed, Rs 100 towards the Prime Minister’s

Page 107 :
105, IX Standard – Mathematics, , Chapter, 10 – Linear Equations in Two Variables, 42, Relief Fund to help the earthquake, victims. Write a linear equation which, satisfies this data. (You may take their, contributions as Rs x and Rs y). Draw, the graph of the same., Ans. Let the contribution of yamini be Rs x and, the contribution of fatima be Rs y., x + y = 100, y = 100 – x, x = 0, y = 100 – 0 = 100, x = 50 , y = 100 – 50 = 50, x = 20, y = 100 – 20 = 80, x, y, , 0, 100, , 20, 80, 100, , Ans. F = (9/5)C + 32, When x =0, F =9 × 0 + 32 =0 + 32 =32, 5, 9, When x =5, F = × 5 + 32 =9 + 32 =41, 5, 9, × 10 + 32, When x = 10, F =, 5, = 9 × 2 + 32 = 18 + 32 = 50, C, F, , 40, 30, , y, (0,100), , x1, , y, , (10,50), , (5,41), (0,32), , 10, –20 –15 –10 –5, –10, , (20,80), , 70, , 5, , 10 15 20 25, , x, , –20, , 60, , –30, , (50,50), , 50, 40, , y1, , x + y = 100, , 30, , ii., , 20, 10, –40 –30 –20 –10, –10, , 10, 50, , 20, , 90, , x1, , 5, 41, 50, , 50, 50, , 80, , 0, 32, , 10 20 30 40 50, , x, , –20, , If the temperature is 30oC, what is the, temperature in Fahrenheit?, Ans. F = (9/5)C + 32, C = 30, F = 9 × 30 + 32, 5, =, F 54 + 32, F = 86, The temperature in Fahrenheit is86o F, , –30, , y1, 8., , In countries like USA and Canada,, temperature is measured in Fahrenheit,, where as in countries like India, it is, measured in Celsius. Here is a linear, equation that converts Fahreheit to, Celsius :, 9, =, F   C + 32, 5, , i., , Draw the graph of the linear equation, above using Celsius for x-axis and, Fahrenheit for y-axis., , iii., , If the temperature is 95oF, what is the, temperature in Celsius?, Ans. F = 9/5C + 32, F = 95o F, o, 9, =, 95, C + 32, 5, 9, = 95 − 32, C, 5, 9 C = 63, 5, 63 × 5, =, C = 35o, 9, C = 35o, 35o C, \ Required temperature =

Page 108 :
106, , Chapter 4 – Linear Equations in Two Variables, iv., , If the temperature is 0oC, what is, the temperature in Fahrenheit and, if the temperature is 0o F, what is the, temperature in Celsius?, Ans. When C = 0 then, =, F 9 ( 0 ) + 32, 5, F = 32o F, , 43, , Ans. y = 3, i. In one variable, , \ Required temperature =, 32o F, =, When, F 0=, then F, , IX Standard – Mathematics, , ( 9 5 ) C + 32, , =, 0 9 C + 32, 5, 9 C = −32, 5, o, −32 × 5 −160, =, C =, C, 9, 9, , y=3, , 3, 2, 1, 0, –1, –2, –3, , ii. In two variables y = 3, y, 3, A (0,3), 2, 1, o, , v., , −160, x1 –5 –4 –3 –2 –1, \ Required temperature =, C, –1, 9, –2, Is there a temperature which is numerically, –3, the same in both Fahrenheit and Celsius? If, yes, find it., , Ans. Let the temperature be ‘y’ numerically., Then, F 9 C + 32, =, 5, 9, y, y + 32, =, 5, 9 y − y =−32, 5, 4 y = −32, 5, 5, y=, −32 ×, 4, y =−8 × 5 =−40, , ( ), , y = − 40, \ Numerical value of required, temperature = −40o, Exercise 10.4, 4.4, , 1., , Give the geometric representations of y, = 3 as an equation, i. in one variable, ii. in two variables, , 1 2 3 4 5 x, , y1, 2., , Give the geometric representations of, 2x+9=0 as an equation, i. in one variable, ii. in two variables, Ans. i. In one variable, 2x + 9 =, 0, 2x = − 9, x = −9, 2, 1, x = −4, 2, –9/2, x1 –5 –4 –3 –2 –1 0 1 2 3 4 5 x, ii. In two variable, 2x + 9 = 0, 2x + 0y + 9 = 0, It is a linear equation in two variable x and, y. Two solutions of given equation 2x + 0y, + 9 = 0 are x = -9/2, y = 0 & x = -9/2, y = 3

Page 109 :
107, IX Standard – Mathematics, , Chapter 10 – Linear Equations in Two Variables, , 44, , (–9/2, 3), (–9/2, 0), , 4, 3, 2, 1, , x1 –5 –4 –3 –2 –1, 1 2 3 4 5 x, –1, –2, –3, –4 y1, Additional Problems, , I., , Multiple Choice Questions, , 1., , The standard form of an linear equation, in one variable is, a) ax + bz = 0, b) ax + c = 0, c) by = c + z, d) ax = 0, , 2., , 3., , The standard form of an linear equation, in two variable is, a) ax + c = 0, b) x + y + z = 0, c) ax + by + c =0, d) ax = 0, , The line x = y pass through, a) (0,1), b) (0,0) c) (1,0) d) (1,1), , 5., , The graph of x = 3 is a straight line, parallel to, a) x - axis, b) y - axis, c) line x = y, d) none of the above, , 7., , 8., 9., , 10., , A point on line x - y = 0 is, a) (1,–1) b) (0,1) c) (1,0) d) (1,1), Ans. 1) b, 2) c, 3) d, 4) b, 5) b, 6) c, 7) c, 8) d, 9) a, 10) d, Answer the following questions, , 1., Draw the graph of the equation y = 2x+1, Ans. y = 2x + 1, x, y, , 0, 1, , 1, 3, , y, , Value of x in the equation 3x = 20 - x, a) 1, b) 10, c)4, d) 5, The line y = mx, , y = 2x + 1, , +4, +3, +2, +1, –5 –4 –3 –4 –1, -1, , x1, , 0 1 2 3 4 5 6, , x, , -2, -3, -4, -5, , y1, , 2., Draw the graph of 3x + y = 6, Ans. 3x + y = 6, x, y, , 0, 6, , 1, 3, +6, +5, , Find the value of k if (4,1) is a solution of, 3x + 2y = k, a) 12, b) 10, c) 14, d) 16, How many lines may pass through two, points., a) 2, b) 0, c) 1, d) infinity, , -1, -1, , +5, , Write the values of a,b & c in the, equation 2x + 3y + 8 = 0, a) 2,8,3, b) 3,2,8 c) 8,3,2 d) 2,3,8, , 4., , 6., , a) passes through origin, b) does not pass through origin, c) is parallel to x - axis, d) is parallel to y - axis, , y, , 2, 0, y, , 3, -3, , y, , +4, +3, +2, +1, , x1, , –5 –4 –3 –4 –1, -1, , 0 1 2 3 4 5 6, , -2, -3, , 3x+y=6, , -4, -5, , y, , 1, , x

Page 110 :
87, , 108, , Chapter--11, 9, CHAPTER, , Areas of parallelograms and triangle, Key Points :, , ●, ●, ●, ●, ●, ●, ●, ●, ●, ●, ●, ●, , The diagonals of a parallelogram divides it into two triangle of equal areas., Area of triangle = 1/2 x base x height, Parallelogram on the same base and between the same parallel lines are equal in areas., The area of a parallelogram is the product of its base and the corresponding altitude, Triangles on the same base and between the same parallel are equal in areas., If a triangle and a parallelogram are on the same base and between the same parallel lies, then, area of the triangle is half of the area of the parallelogram., The area of a trapezium is half of the product of its height and the sum of parallel sides., Triangles having equal areas and one side of one of the triangles is equal to one side of the, other then their corresponding altitudes are equal., A median of a triangle divides it in two triangles of equal areas., If two figures are congruent, then they have equal areas., Diagonals of a parallelogram divides it into four triangles of equal areas., The line segment joining the mid points of a pair of opposite sides of a parallellogram divides, it into two equal parallelogram., , Exercise 11.1, 9.1, , 1., , Which of the following figures lie on the same base and between the same parallels. In, such a case, write the common base and the two parallels.

Page 111 :
Chapter 11 – Areas of parallelograms and triangle, , 88, , 109, IX Standard – Mathematics, , Ans. i. Triangle PDC and quadrilateral ABCD lie on the same base DC and between the same, parallel DC and AB., iii. DTRQ and parallelogram SRQP lie on the same base RQ and between the same parallel, RQ and SP., v. Quadrilateral APCD adn ABQD lie on the same base AD and between the same parallels, AD and BD., ● ii, iv and vi are not having same base and not lies on the same parallels., Exercise 11.2, 9.2, , 1., , In Fig 9.15, ABCD is a parallelogram, AE perpendicular DC and CF perpendicular AD., If AB = 16 cm, AE = 8 cm and CF = 10 cm, Find AD., Ans. Area of parallelogram ABCD = CD x AE [CD = AD], = 16 x 8, = 128 cm2, AD x =, CFAD x CF, Area of parallelogram =ABCD, 128, = AD × 10, 128, Fig 11.15, AD, = = 12.8cm, 10, 2., , If E,F,G and H are respectively the mid-points of the sides of a parallelogram ABCD,, 1, show that ar ( EFGH ) = ar ( ABCD ), G, D, C, 2, P, Ans. In parallelogram ABCD. E,F,G and H, S, are midpoints of the sides. of parallelogram., H, F, To prove :, O, EFGH = 1 area ABCD, 2, R, Q, Construction:Join OE, OF, OG, OH, AC & BD, B, A, E, AC and BDProof :In DBCD, FG ||BD... (1), , le,  In a D line joining the mid points of any two sides parallel to third side , , In D BAD, EH || BD... ( 2 ), From (1) & ( 2 ), ,  In a D le line joining the mid points of any two sides parallel to third side , , EH||FG ... ( 3), Similarly, we can prove that, EF||HG ... ( 4 ), From ( 3) and ( 4 ), Quadrilateral EFGH is a parallelogram, \ Fis the midpoint of BC and O is the midpoint of AC, FO||AB... ( 5 ), AB||CG, FO = 1 AB, 2, 1, =, CD, 2, ,  In a D le line joining the mid points of any two sides parallel to third side 

Page 124 :
122 9 – Areas of parallelograms and triangle, Chapter, Ans., , IX Standard – Mathematics, 101, , ar ( DDRC ) =, ar ( DDPC ) and ar ( DBDP ) =, ar ( DARC ), To prove:Both the quadrilateral ABCD and DCPR are trapeziums, Proof :ar ( DDRC ) =, ar ( DDPC ) ... (1) [ Given ], DDRC and DDPC are on same base CD and will have equal corresponding altitudes and will, lie between same parallels, \ CD||PR, \ DCPR is a trapezium, , [One pair of opposite sides are parallel], , ar ( DBDP ) =, ar ( DARC ), ar ( DBDC ) + ar ( DDPC ) = ar ( DADC ) + ar ( DDRC ), ar ( DBDC ) =, ar ( DADC ), , [ From1], , But DBDC and DADC are have same base CD and will have equal corresponding altitudes and will, lie between the same parallels, \ AB || CD, \ ABCD is a trapezium, Exercise 11.4, 9.4 (Optional), 1., Ans., , Parallelogram ABCD and rectangle ABEF are on the same base AB and have equal areas., Show that the perimeter of the parallelogram is greater than that of the rectangle., F, , D, , E, , C, , A, B, Given : ABCD is a parallelogram and ABEF is are on same base AB and between the same, parallels AB and CF. Therefore, ar(||gm ABCD) = ar(rec+.ABEF), t, To prove :, AB+BC+CD+AD > AB+BE+EF+AF, Proof : AB = CD, [Opposite side of parallelogram are equal], AB = EF ...(1), [Opposite side of parallelogram are equal], Adding AB to both sides of eqn (1), we get, AB+CD = AB+EF ...(2), \If all the segments that can be drawn to a given line from not lying on it, the perpendicular, segment is the shortest., \BE < BC and AF < AD, or BC > BE, AD > AF, \BC+AD > BE + AF ....(3)

Page 134 :
111, , 132, , Chapter - 10, CHAPTER - 12, , Circles, Circles, , Key Points :, , ●, ●, ●, ●, , Circle :- A circle is the collection of all points in a plane, which are equidistant from a fixed, point in the plane., Chord :- Line segment joining two end points on the circle., Radius :- It is the distance between fixed point to any point on the circle., Diameter :- A chord which pass through the centre of a circle is called diameter., , ( or ) r, =, d 2r, =, ●, ●, ●, ●, ●, ●, ●, ●, ●, ●, ●, ●, ●, ●, ●, ●, ●, ●, ●, ●, ●, , d, 2, , Arc :- A part of a circle is called Arc., Minor Arc :- Smaller part of a circle., Major Arc :- Bigger part of a circle., Segment :- The region bounded by Arc and chord., Minor segment :- The region bounded by Minor Arc and chord., Major segment :- The region bounded by Major Arc and chord., Sector :- The space bounded by two radii., Concentric circles :- Circles having the, he same centre but different radii., Congruent circles :- Circles having same radii but different centres., Equal chords of a circle subtend equal angles at the centre., If the angles subtended by two chords of circle at the centre are equal, the chords are equal., The perpendicular from the centre of a circle to a chord bisects the chord., The line drawn through the centre of a circle to bisect a chord is perpendicular to the chord., There is one and only one circle passing through three non-collinear points., Equal chords of a circle are equidistant from the centre., Chords equidistant from the centre of a circle are equal., If two arcs of circle are congruent, then their corresponding chords are equal and conversely if, two chords of a circle are equal, then their corresponding arcs are congruent., Congruent arcs of a circle subtend equal angles at the centre., The angle subtended by an arc at the centre is double the angle subtended by it at any point on, the remaining part of the circle., Angle in the same segment of a circle are equal., Angle in a semicircle is a right angle.

Page 135 :
133, IX Standard – Mathematics, , Chapter, 112 12 – Circles, ●, ●, ●, ●, ●, , Angle in a minor segment is obtuse angle., Angle in a major segment is Acute angle., If a line segment joining two points subtends equal angles at two points lying on the same side, of the line containing the line segment, the four points lie on a circle., The sum of either pair of opposite angles of a cyclic quadrilateral is 180o., If sum of a pair of opposite angles of a quadrilateral is 180o, the quadrilateral is cyclic., Exercise 12.1, 10.1, , 1., (i), , Fill in the blanks:, The centre of a circle lies in __________, of the circle, (exterior/ interior), (ii) A point, whose distance from the centre, of a circle is greater than its radius lies in, _______of the circle, (exterior/ interior), (iii) The longest chord of a circle is a, _________ of the circle., (iv) An arc is a __________ when its ends, are the ends of a diameter., (v) Segment of a circle is the region between, an arc and ____________ of the circle., (vi) A circle divides the plane, on which it, lies, in __________ parts., Ans. i) interior, ii) exterior, iii) diameter, iv) semicircle, v) chord, vi) three, 2., , Write True or False: Give reasons for, your answers., (i) Line segment joining the centre to, any point on the circle is a radius, of the circle., (ii) A circle has only finite number of, equal chords., (iii) If a circle is divided into three, equal arcs, each is a major arc., (iv) A chord of a circle, which is twice, as long as its radius, is a diameter, of the circle., (v) Sector is the region between the, chord and its corresponding arc., (vi) A circle is a plane figure., , Ans. i) true because all the points on the circle, are equidistant from the centre., ii) False :- because in a circle we can write, infinite number of chords., iii) False :- Because for each arc, the, remaining arc will have greater length., iv) True, because of definition diameter., v) False, It is a definition of segment., vi) True, It is a part of a plane., Exercise 12.2, 10.2, , 1., , Ans., , Recall that two circles are congruent, if they have the same radii. Prove, that equal chords of congruent circles, subtend equal angles at their centres., , O, , O1, B, , D, , C, A, Given :- Two congruent circles with, centres O and O1, AB and CD are two, equal chords., To prove :AOB = CO1D, OA = O1C {Radii of congruent circle}, OB = O1D {Radii of congruent circle}, AB = CD {equal chords}, \DAOB ≅ DCO1D {SSS congruent}, \ AOB =, CO1D {C.P.C.T}, 2., Ans., , Prove that if chords of congruent circles, subtend equal angles at their centres,, then the chords are equal.

Page 136 :
134 10 – Circles, Chapter, , O, , IX Standard – Mathematics, 113, BC., Let these intersect at O., \O is the centre of the circle., , O1, , B, A, D, C, Given :- Two congruent circles with, centres O and O1, AOBand CO1D are, two equal angles subtended by chords AB, and CD., To prove :- AB = CD, Proof : In DAOB and DCO1D, OA = O1C {Radii of congruent circle}, OB = O1D {Radii of congruent circle}, AOB = CO1D {Given}, \ DAOB ≅ DCO1D {SAScongruent}, \AB = CD {C.P.C.T}, Exercise 12.3, 10.3, , 1., , Ans., , Draw different pairs of circles. How, many points does each pair have in, common? What is the maximum, number of common points?, i), , ii), , iii), , No point common, , One point common, A, , B, Two points common, Maximum number of common points is, two., 2., , Suppose you are given a circle. Give a, construction to find its centre., Ans. i) Take any three points A, B and C on the, circle., ii) Join AB and BC, iii) Draw perpendicular bisector of AB and, , O, , A, , C, , B, 3., , Ans., , If two circles intersect at two points,, prove that their centres lie on the, perpendicular bisector of the common, chord., A, O, , P, , O1, , B, Given :- Two circles with centres O and, O1, intersecting at A and B., To prove :OO1 is the perpendicular bisector of AB., Construction :- Join OA, OB, O1A and, O1B and OO1 intersect AB at P., Proof :- In DOAO1 and DOBO1, OA = OB {Radii of circle}, O1A = O1B {Radii of circle}, OO1 = OO1 {Common side}, \ DOAO1 ≅ DOBO1 {SSScongruent}, AOO1 = BOO1 [ C.P.C.T ], AOP = BOP .....(1), (1), In D le AOP and D le BOP, , OA = OB [ Radii ], , OP = OP [ Common side ], AOP = BOP  From (1) , But APO + BOP =, 1800 [ Linear pair ], = BPO, = 90o, APO, \ OO1 is the perpendicular bisector of AB.

Page 137 :
135, IX Standard – Mathematics, , Chapter 12 – Circles, , 114, , equidistant from centre}, OE= OE [Common], OME, = ONE, = 90o, , Exercise 12.4, 10.4, , 1., , Ans., , Two circles of radii 5 cm and 3 cm, intersect at two points and the distance, between their centres is 4 cm. Find the, length of the common chord., , [ON & OM perpendicular], \DOME ≅ DONE [RHS congruent], ME = NE [C.P.C.T], AM + ME = DN + NE, [\ AM = DN = ½AB = ½CD], AE = DE, AB – AE = CD – DE, | AB = CD, BE = CE, , X, , A, , 4cm B, 3., Y, , distance between centres of two circles is, 4cm. The line joining their centres is the, perpendicular bisector of their common, chord., \ Length of common chord = XY = 2BX, (or) 2BY = 2 × 3 = 6cm [BX = BY radii of, small circle], 2., , Ans., , Ans., , If two equal chords of a circle intersect, within the circle, prove that the line, joining the point of intersection to the, centre makes equal angles with the, chords., , A, , If two equal chords of a circle intersect, within the circle, prove that the segments, of one chord are equal to corresponding, segments of the other chord., , O, , D, , E, C, , B, Two equal chords AB and CD of a circle, with centre ‘O’ intersect with in the circle, their point of intersection is E., To prove :- OEA = OED, , A, O, M, , D, , Construction : Join OA and OD, Proof :- In DOEA and DOED, OE = OE [common], OA = OD [Radii of a circle], AE = DE [ Proved in example 2], DOEA ≅ DOED [SSS congruency], OEA = OED [ C.P.C.T ], , N, E, , C, , B, Given :- A circle with centres O, two equal, chords AB and CD intersect at E., To prove :- AE = DE and CE = BE, AB ON⊥CD., Construction :- Draw OM⊥OB,, Join OE., Proof :- In DOME and DONE, OM = ON {equal chords of a circle are, , 4., , If a line intersects two concentric circles, (circles with the same centre) with, centre O at A, B, C and D, prove that

Page 138 :
136 10 – Circles, Chapter, , IX Standard – Mathematics, 115, , AB = CD., , O, , C, , 5m, , R, , D, , O, M, , K, L, , A, , B, , Ans., , O, , A, , B, , C, , D, , M, , Given :- A line intersects two concentric, circles with centre O at A, B, C and D., Construction : Draw OM perpendicular, BC., To prove :- AB = CD, Proof :- The perpendicular drawn from, the centre of a circle to a chord bisects the, chord, AM = DM → (1), BM = CM → (2), Substractions (2) from (1), AM – BM = DM – CM, AB = CD, 5., , Ans., , 6m, , 6m, , Three girls Reshma, Salma and Mandip, are playing a game by standing on a, circle of radius 5m drawn in a park., Reshma throws a ball to Salma, Salma, to Mandip, Mandip to Reshma. If the, distance between Reshma and Salma, and between Salma and Mandip is, 6m each, what is the distance between, Reshma and Mandip?, , S, Let KR = ‘a’m, area DleORS = area of DleORK + area of, DleRKS, ( OK ) ( KR ) ( KS) ( KR ), 1 bh , area =, =, +, 2 , , 2, 2, (, ), KR OK + KS, a ×5, =, =, 2, 2, 5a, area of D le ORS = → (1), 2, area of D le ORS= 1 × b × h, 2, = 1 × RS × OL, 2, = 1 × 6 × OL, 2, = 3 OR 2 − RL2, 2,  RS , = 3 ( 5) − , ,  2 , , 6, = 3 25 −  , 2, = 3 25 − ( 3), , 2, , 2, , 2, , = 3 25 − 9, = 3 × 16, = 3 × 4 = 12 → ( 2 ), From equation (1) & ( 2 ), 5a, = 12, 2, 5a = 24, 24, = 4.8cm, 5, 2 4.8 =, 9.6m, RM = 2KR =×, , =, a

Page 139 :
= 3 ( Area of DQOR ), 1, = 3 × × QR × OS, 2, 3, = ( 2QS) OS, 137, 2, IX Standard – Mathematics, , Chapter 12 – Circles, , 116, , = 3QS 400 − x 2, , Hence, the distance between Reshma, = 3x 400 − x 2 ... ( 2 ), and mandip is 9.6m, 6., , Ans., , From (1) & ( 2 ), , A circular park of radius 20m is situated, in a colony. Three boys Ankur, Syed and, David are sitting at equal distance on its, boundary each having a toy telephone, in his hands to talk each other. Find the, length of the string of each phone., , 3x 400 − x 2 =, 3x 2, 3 400 − x 2 =, x, Squaring both sides, 3 ( 400 − x 2 ) =, x2, , P, , 1200 − 3x 2 =, x2, 1200 = 4x 2, , 20m, , =, x2, , O, , Q, , =, x, , 20, , m, , m, , 20, , S, , =, x 10, =, 3 m 10 3m, , (, , =, QR 2=, ( QS) 2 10 3, , R, , Let QS = xm, OP = OQ = OR = 20cm, In right angle Dle OQS, OQ2 = QS2 + OS2, (20)2 = (x)2 + OS2, OS2 = 400 – x2, =, OS, , 1200, = 300, 4, =, 300, 100 × 3, , QR = 20 3m, Exercise 10.5, 12.5, , 1., , 400 − x 2, , 3, 2, Area of equilateral DPQR =, ( side ), 4, 3, 2, =, ( QR ), 4, 3, 3, 2, = =, 4QS2, ( 2QS), 4, 4, = 3QS2, , 12, In Fig 10.36,, A,B and C are three points, on a circle with centre O such that BOC, = 30o and AOB = 60o . If D is a point on, the circle other than the arc ABC, find, ADC., , = 3x 2 ... (1), Area of DPQR= Area of DQOR, + Area of DOPQ + Area of DPOR, = 3 ( Area of DQOR ), 1, = 3 × × QR × OS, 2, 3, = ( 2QS) OS, 2, = 3QS 400 − x 2, = 3x 400 − x 2 ... ( 2 ), From (1) & ( 2 ), , ), , Ans., , ADC = 1 AOC, 2, 1, =, AOB + BOC ), 2(, = 1 ( 60o + 30o ), 2, 1, =, × 90o, 2, = 90, = 45o, 2, ADC = 45o

Page 142 :
140 10 – Circles, Chapter, , IX Standard – Mathematics, 119, , 8., If the non-parallel sides of a trapezium are equal, prove that it is cyclic., Ans., A, B, , C, E, D, ABCD is a trapezium whose non-parallel sides are equal AD = BC, To prove : Trapezium ABCD is cyclic, Construction : Draw BE || AD, Proof : AB || DE [Given], AD || BE [Construction], \ ABCD is a parallelogram, BAD = BED.. (1) ( Opposite angle of a parallelogram ), AD = BE... ( 2 )( Opposite sides of parallelogram ), AD = BC... ( 3)( Given ), From ( 2 ) & ( 3), BC = BE, BCE.. ( 4 )( angles opposite to equalsides are equal ), \ BEC =, BEC + BED =, 180o [ Linear pair ], 180o  From (1) & ( 4 ) , ⇒ BCE + BAD =, , \ Trapezium ABCD is a cyclic ( Sum of the pair of opposite angles180o ), , 9., , Two circle intersect at two point B and C. Through B, two line segments ABD and PBQ, are drawn to intersect the circles at A,D and P, Q respectively. Prove that <ACP = <QCD., , Ans. Two circles intersect at two points B and C. Through B, two line segments ABD and PBQ are, drawn to intersect the circles at A,D and P, Q respectively., To prove :, ACP = QCD, , Proof : ACP = ABP.. (1)( angles in the same segment are equal ), QCD = QBD... ( 2 ) ( angle in the same segment are equal ), ABP = QBP.... ( 3) ( V.O.A ), From (1) , ( 2 ) & ( 3), ACP = QCD

Page 143 :
IX Standard – Mathematics, 141, , Chapter, 120 12 – Circles, 10., , Ans., , If circles are drawn taking two sides of, a triangle as diameters, prove that the, point of intersection of these circles lie, on the third side., , To prove :, CAD = CBD, Proof :ACis the common hypotenuse, ABC and ADC are two right triangles., o, ABC, ADC, = 90, =, \ Points A, B, D and C are concyclic, \ DCis a chord, CBD, \ CAD =, , A, , B, , (angles in the same segment are equal), , C, , D, , Two circles touches as shown in the figure, AB and AC are two diameters of the, triangle ABC. D intersects on BC., To prove : D lies on the third side BC of, ABC., D ABC, Construction : Join AD, Proof : Circle described on AB as diameter, intersects BC in D., ADB = 90o ( angle in a semicircle ), , 12., Ans., , Prove that a cyclic parallelogram is a, rectangle., A, , But ADB + ADC =, 180o [ Linear pair ], , 1, , ADC = 90o, The two circles intersect in D., , 11., , B, 2, , D, , C, , Now, ADB + ADC =, 180o, \ Points B, D, C are collinear, \ D lie on BC, , Given : ABCD is a cyclic parallelogram., To prove : ABCD is a rectangle., Proof : ABCD is a cyclic quadrilateral, 1+ 2 =, 180o ... (1) (Opposite angles of, , ABC and ADC are two right triangles, with common hypotenuse AC. Prove, that CAD = CBD, , cyclic quadrilateralis180o ), \ ABCD is a parallelogram, , Ans., , 1 = 2... ( 2 ), From (1) & ( 2 ), , A, , 1= 2= 90o, \ Parallelogram ABCD is a rectangle, B, , O, , Exercise 12.6, 10.6, , 1., C, D, Given : ABC and ADC are two right, triangles with common hypotenuse AC., , Ans., , Prove that the line of centres of two, intersecting circles subtends equal, angles at the two points of intersection.

Page 144 :
142, Chapter, 1010, – Circles, Chapter, – Circles, CC, Chapter r10r– Circles, r, 1, , 1, , A A, r1 rr1, , r2, , 2, , BB, r, r2 2, r, 1, D 2, D, A, B, Given, : Let, twocircles, circles, withrespective, respective, Given, : Let, two, with, r, r, 1 and B2 intersect each other at, centers A, centers A and DB intersect each other at, points C and D. We have to prove, points, C andLet, D. We, to prove, Given, two have, circles, with respective, ACB =: ADB, ACB, = ADB, centers, A, and, B, intersect, Proof :In DABC and DABD each other at, points, and D., WeDABD, have to prove, Proof, :In C, DABC, and, = BD, AC, ( radii ), =, ACB, ADB, AC = A, BD ( radii ), = BD, BC, ( radiiand, ) DABD, Proof, :In DABC, BC = BD ( radii ), AB = AB, common, AC, BD ((radii, ) ), C, , ( common ), ABDC.P.C.T, \ DABC, ], =≅ D, ACB, ADB, [ [SAScongruency, = AB, AB, ( common, ) ], ACB, ADB, C.P.C.T, ], \ D=ABC, ≅ D[ABD, [SAScongruency, ], AB = AB, , \, DABC, ABD, = BD ≅ (Dradii, BC, ) [SAScongruency], , 2., , Two chords AB and CD of lengths 5, , = ADB, ACB, ] of lengths, cm, and, 11AB, cm[ C.P.C.T, respectively, of a circle, Two, chords, and, CD, 5, are, parallel, to, each, other, are, cm and 11 cm respectively of aand, circle, 2., Twoopposite, chords sides, AB and, CDcentre., of lengths, of its, the5, areonparallel, to each, other, andIf are, cm, and 11, cm respectively, of isa 6circle, distance, between, AB, and, CD, cm,, on opposite sides of its centre. If the, are, parallel, eachcircle., other and are, find the, radiustoofAB, the, distance, between, and, CD, is 6 cm,, on, opposite, sides, of, its, centre. If the, Ans., finddistance, the radius, of, the, circle., 5/2CD, cm is 6 cm,, between AB and, Ans., find the radius N, of the circle., 5/2 cm, (6-x) r, Ans., N 5/2 cm B, A, 0r, r 5/2 cm, (6-x) xN, 0 Mr r, (6-x), D, x0, r, D circle be rcm., GivenC: Let the, Mxradius of the, , 2., , MC== 11 cm, cm, \, MD == MC, \ MD, 22, ON, AB, ON ⊥, ⊥ AB, 11, N, is, the=mid, mid, point, AB, MC−−=point, cm, \, N MD, is the, ofofAB, 2, IX11Standard, – 5Mathematics, 1, 5, 1, 121, ON, NB, AN, AB, 5) ) cm, cm 121, =⊥ AB, = AB, = (=, AN, 5(=, =, =, 22, 22, 22, N is the mid − point of AB, In right angle, angletriangle, triangleONB, ONB, 1, 1, 5, NB, 5pythogoras, =2 AN, = 2 AB, =2 By, (=, ) cm 121, , 2, 2+, 2 2By pythogoras, 2, 2, OB, ON, NB, =, OB, = ON + NB , , theorem,  theorem, , In right angle triangle, ONB, 2, r2 equals (611– 2x), + (5/2)2 ......(1), 2,   2  By pythogoras , 2 2 2, 2 triangle, r=, xx 2ON, =, ++  211, OMB, OB, =, +NB ......, rIn, (22) ), (theorem, ,  222 , 2, 2, , ,  + MD, OD = OM, From (1) & ( 2 ) 2we get, From, (21) & 11, ( 2) we get, 2, , r= x 2+   2 ... ( 2 ), 2, (66 −− xx ) 2 ++( 5252) 2 ==xx2 2++(11112 ) 2, (From ()1) &(( 2 2) we, )25get (1212 ), 2, , 2, , 36 − 12x, + x 2 + 2 25= x 2+ 121, 2, 2, 36, +4, x ) ++ x5 + 4=x=2 +x 11, ( 6 −− 12x, 2 4, 24, 144 96, 12x, = 144 − 2 9625, 121, 36, − 12x4+ x− 4+, = x2 +, 12x, =, 4, 4, 4, 484, 12x = 144= 12, 96, 12x, == 448 =−12, 12x, 4, 12 44, x =481, =, 12x 12, = 12, =, x =4 1, =, x = 112, 12, =, xPutting, = 1= x1=1 in eqn ( 2 ), , ( ), , ( ), , 12, , 2, Putting, x2 = 1 2x =111ineqn ( 2 ), , r (1) +   2, =, 2ineqn, Putting 2x =1 11,  ( 2), r 2 1(1) 121, =, +  2, 2 , r 22 = +2 11, r (11) +4  , =, 1 121, 2, r 22= 4 + 121, 125, r2 =, 4 =, 1 +121, r = 4+ 4, 4, 125, 14 121, 4, r2 =, =, 5 5+, r 2= 4 121, 4 125, 4, r =2 +, =, 4, 4, 4, 5 5, r=, 5 5, 5 of, 5 a circle is, radius, r= 2, 2, 2, 5 5, D, Let OM = x cmM, radius, of, a, circle, is, 3., The lengths of two, chords of a, 5 parallel, 5, Then, ONthe, = (6radius, – x) cm, radiusare, of a6circle, is 82 cm. If the smaller, Given, : Let, of the circle be rcm., circle, cm, and, 2, OM, CDof the circle be rcm., LetGiven, OMperpendicular, =: xLet, cmthe radius, chordlengths, is at of, distance, 4 cm chords, from the, 3., The, two parallel, of a, Let, OM, =, x, cm, \M, is, the, mid-point, of, CD, Then ON = (6 – x) cm, 3. circle, The, lengths, of, two, parallel, chords, of a, centre,, what, is, the, distance, of, the, other, are, 6, cm, and, 8, cm., If, the, smaller, ON = (6 – x), The, perpendicular, from the centre of a, OMThen, perpendicular, CDcm, circle, and, 8 cm.4 Ifcm, the from, smallerthe, chord are, from, thedistance, centre?, chord, is 6atcm, OM, perpendicular, CD the chord., circle, to, a, chord, bisects, \M is the mid-point of CD, chord, is, at, distance, 4, cm, from, the, Ans. centre, what is the distance of the other, \M is the mid-point, of CD, 11from, centre, what is the distance of the other, The\perpendicular, the centre of a, =, =, MD, MC, cm, The perpendicular, the centre of a, chord from, the, centre?, 3 centre?, cm, E 8 cm B, A the, 2 from, circle, to atochord, bisects, thethechord., chord from, circle, a, chord, bisects, chord., Ans., ON ⊥ AB 11, r, Ans., 11, 4 cm D, \ MD, = −=point, MC, cm of AB, C 400, \, =mid, MC, N MD, is=the, cmEE0388cm, cm BB, A r33cm, 2 2 cm, A, 1, 1, 5, ONON, ⊥, r, ⊥ AB, NB, AN, AB, 5), cm, =AB, =, =, (=, 400r, cm DD, 4 400, cm, 2 of AB, 2, 2, 44cm, C, C, N isNthe, mid, point, −, is the mid − point of AB, 0, r, 0, In right angle triangle ONB, r, 1 1, 11, 55, NB, AB, 5, cm, =NB, =, =, =, AN, AB, 5, cm, =AN, =, =, =, (, ), (, ), By, pythogoras, , , 2, 2 NB22 2, 22, =, OB, ON22 +, , theorem, ONB, , In right, angle, triangle, ONB, In right, angle, triangle, 2,  11  2By, 2 2 2,  By, pythogoras, 2 ... ( 2, +2 +2 NB, r2=, x ON, ) pythogoras , =, +NB, OB, =, OB, ON, , , , 2,   theorem,   theorem, 

Page 145 :
143, IX Standard – Mathematics, , Chapter, 122 12 – Circles, Given : Let AB = 6 cm and CD = 8 cm are, 0. Join OA, the chords of circle with centre 0/, and OC., Since perpendicular from the centre of the, circle to the chord bisects the chord., AE, = EB, = 1 AB, 2, = 1 × 6= 3cm, 2, and CF= FD= 1 CD= 1 × 8= 4 cm, 2, 2, In right angle triangle AOE, 2, =, OA, AE 2 + OE 2 [ Pythogoras theorem ], , r 2 =32 + 42 =9 + 16, 2, , r = 25, r = 25, r = 5cm, Perpendicular distance of chord CD, from the centre 0 of OF, In right angle DOFC, 2, =, OC, CF2 + OF2 [ Pythagoras theorem ], 2, , 2, , r= 4 + OF, , ( 5)=, 2, , 2, , 16 + OF2, , 2, , OF= 25 −16, 2, OF=, 25 −16, , OF2 = 9, OF, = =, 9 3cm, Distance of other chord from the, centre is 3cm., 4., , Ans., , Let the vertex of an angle ABC be, located outside a circle and let the sides, of the angle intersect equal chords, AD and CE with the circle. Prove that, ZABC is equal to half the difference of, the angles subtended by the chords AC, and DE at the centre., , A, , F, 0, , E, B, D, , C, , Verrtex B of ABC is located outside the, circle with centre 0., Side AB intersect chord CF at point E and, side BC intersect chord AD at point D with, the circle. Join OA, OC, OE and OD., Prove that=, : ABC 1=, AOC DOE ], 2[, , [Angle subtended by an arc at the, centre of the circle is twice the angle, subtended by the same arc at any point, in the alternate segment of a circle]., 1 AOC = AEC ... (1), 2, Similarly 1=, DEO DCE ... ( 2 ), 2, Subtracting ( ii ) from ( i ), , AOC − DEO ], 2[, = AEC − DCE... ( 3), 1, , angles in the same , AEC = ADC ... ( 4 ) , , segment are equal , angles in the same , DCE = DAE... ( 5 ) , , segment are equal , , Using ( 4 ) and ( 5 ) in ( 3), AOC − DOE ], 2[, = ADC − DAE... ( 6 ), 1, , In DADB, ADC, =, , DOE + ABD... ( 7 ), ,  Exterior angle is equalsum of the , interior opposite angles, , , , 1 [ AOC − DOE ], 2, = DAE + ABD − DAE, ⇒ 1 [ AOC − DOE ] =, ABD, 2, ABC, ( or ) 1 2 [ AOC − DOE ] =

Page 146 :
, Also ADE + ADC =, 180o, , , , [ Linear pair ], , ABC, 180o ... ( 2–)Mathematics, =, IX Standard, 123, From (1) & ( 2 ), ADC, =, , 144 10 – Circles, Chapter, 5., , Ans., , Prove that the circle drawn with any, side of a rhombus as diameter, passes, through the point of intersection of its, diagonals., C, D, , B, , E, 0, , A, Let ABCD be a rhombus in which, diagonals AC and BD intersect each other, at point E. We know that diagonals of a, rhombus bisect and perpendicular to each, other., \ AEB =, 90o, , and if we draw a circle with side AB as, diameter, it will definitely pass through, point E. Because AEB = 90o will be, angle in a semicircle., 6., , Ans., , AED + ABC = ADE + ABC, AED = ADE, \ In triangle ADE, AE = AD, \ Sides opposite to equal angles, of a triangle are equal, , ABCD is a parallelogram. The circle, through A, B and C intersect CD, (produced if necessary) at E. Prove that, AE = AD., E D, , C, , A, B, Given : ABCD is a parallelogram. The, circle through A,B and C intersects CD., To prove : AE = AD, Proof : In cyclic quadrilateral ABCE, AED + ABC =, 180o ... (1), Oppsoite angle of a cyclic, , quadrilateral are supplementary , , , o, Also ADE + ADC =, 180, , [ Linear pair ], ADC, =, , ABC, = 180 ... ( 2 ), o, , 7., , Ans., , AC and BD are chords of a circle which, bisect each other. Prove that (i) AC, and BD are diameters, (ii) ABCD is a, rectangle., C, , D, 0, , A, B, Given : AC and BD are chords of a circle, that bisect each other., To prove :, i. AC and BD are diameters, ii. ABCD is a rectangle, Construction : Join AB,BC,CD and DA, Proof :, i. A = 90o,  Angle in a semi , \ BD is a diameter , , o, circle is 90, , o, D = 90, \ ACis a diameter, Thus, AC and BD are diameters, ii.Let the chords AC and BD intersect, each other at O.Join AB, BC, CD, and DA, In DOABand DOCD, OA = OC [ Given ], OB = OD [ Given ], AOB = COD [V.O.A], [ Vert.opp s], \ DOAB = DOCD [SAS], \ AB =, CD [ C.P.C.T ], ⇒ AB =, CD... (1), , From (1) & ( 2 ), , Similarly, we can show that, , AED + ABC = ADE + ABC, AED = ADE, \ In triangle ADE, , AB ≅ CD, , ... ( 2 ), , Adding (1) & ( 2 ) , we get, AB + AD ≅ CD + CB

Page 147 :
AOB = COD [ Vert.opp s ], \ DOAB = DOCD [SAS], \ AB =, CD [ C.P.C.T ], Chapter, 124 12 – Circles, ⇒ AB =, CD... (1), Similarly, we can show that, , IX Standard – Mathematics, 145, 9., , ... ( 2 ), , AB ≅ CD, , Adding (1) & ( 2 ) , we get, AB + AD ≅ CD + CB, ⇒ BAD ≅ BCD, ⇒ BD divides the circle into two equal, parts and the angle of a semi − circle is, 90, , o, , and C 90o, =, \ A 90o =, Similarly, we can show that, o, =, B 90, =, and C 90o, , \ A = B = C = D = 90o, ⇒ ABCD is a rectangle, 8., , Bisectors of angles A, B and C of a, triangle ABC intersect its circumcircle, at D, E and F respectively. Prove that, the angles of the triangle DEF are 90° ½ A, 90° – ½ B and 90°– ½ C., Ans. Given : Bisectors of angles A,B and C of, a triangle ABC intersect its circumcircle at, D,E and F respectively., To prove : The angles of the DDEF are 90o, E, A, C, F, , D, B, Construction : Join DE, EF and FD., Proof :, FDE, = FDA, = FCA + EBA, = 1 C+ 1 B, 2, 2, C + B 180o − A, ⇒=, =, D, 2, 2, A, o, = 90 −, 2, Similarly, we can show that, B, C 90o −, =, 2, C, o, and=, F 90 −, 2, , Ans., , Two congruent circles intersect each, other at points A and B. Though A any, line segment PAQ is drawn so that P, Q, lie on the two circles. Prove that BP =, BQ., P, , A, , Q, , B, Given : Two congruent circles intersect, each other at points A and B. A line through, A meets the circles in P and Q., To prove : BP = BQ, Proof : AB is common chord of two, congruent circles,  Angles subtended by , AQB , \ APB =, , equal chords are equal , Sides opposite to equal angle , BQ , \ BP =, , are equal, , , 10. In any triangle ABC, if the angle, bisector of ∟A and perpendicular, bisector of BC intersect, prove that, they intersect on the circumcircle of, the triangle ABC., Ans. Given : Bisector AP of angle A of DABC, and the perpendicular bisector PQ of its, opposite side BC intersect at P., To prove : P lies on the circumcircle of the, triangle ABC., Construction : Draw the circle through, three non - collinear points A,B and P., Proof :, BAP = CAP [ AP is the bisector of BAC], ⇒ BP ≅ CP, ⇒ chord BP =, chord CP, BP = CP... (1), , A, , In DBMP and DCMP, , 1 2, , BM = CM [ Given ], , BP = CP  By (1) , MP = MP [ Common ], , B, , \ DBMP = DCMP [SSS], \ BMP =, CMP [ C.P.C.T ], But BMP + CMP =, 180o, , M, , C, P

Page 148 :
In DBMP and DCMP, BM = CM [ Given ], , CP–Circles, By (1) , Chapter, 146BP =10, MP = MP [ Common ], \ DBMP = DCMP [SSS], , IX Standard – Mathematics, 125, 6., , A chord of length 16cm of a circle is, a distance of 6cm from its centre. The, radius of a circle is, a) 4cm, b) 6cm c) 8cm d) 10cm, , 7., , The region between a chord and either, of the arcs is called, a) an arc, b) a sector, c) a segment, d) a semicircle, , 8., , cyclic quadrilateral, of that circle, then, , CMP [ C.P.C.T ], \ BMP =, But BMP + CMP =, 180o, \ BMP = CMP = 90o, ⇒ PM is the right bisector of BC, , Aliter :, Assume that C does not lie on the, circle through A,B and P. Let this circle, intersect the side AC at C1., APB = ACB [ Given ], ,  Angle in the , APB = AC1B , , same segment , \ ACB =, AC1B, ⇒ C and C1 coincide, ⇒ The assumption that the point C, does not lie on the circle is false, \ A, B, P and C are concyclic., Additional Problems, , I., , Multiple Choice Questions, , 1., , How many diameters can be drawn in a, circle., a) 1, b) 2, c) Finite d) Infinite, , 2., , The longest chord of a circle is called, a) Radius, b) Diameter, c) Sector, d) Segment, , 3., , 4., , 5., , The angle formed in the minor segment, is, a) Acute angle, b) Right angle, c) Obtuse angle, d) Straight angle, The angle formed in the major segment, is, a) Acute angle, b) Right angle, c) Obtuse angle, d) Straight angle, The angle formed in the semi-circle is, a) Acute angle, b) Right angle, c) Obtuse angle, d) Straight angle, , Diagonals of a, are the diameter, quadrilateral is a, a) Parallelogram, c) Rectangle, Ans. 1) d, 2) b, 3) c, 4) a, 5) b, 6) d, 7) c, 8) c, , b ) Square, d) Trapezium, , II. Answer the following questions, , 1., , In the given figure, 0 is the centre of the, circle. The angle subtended by ar BCD, at the centre is 140o . BC is produced to, P. Determine ∟BAD and ∟DCP., A, o, B, , Ans., , D, C, , P, , BAD = 1 BOD, 2, 1, BAD, =, × 140, 2, BAD = 70o, ABCD be a cyclic quadrilateral, A+ C=, 180o, =, C 180 − 70o, BCD = 110o, Also DCP + BCD =, 180o, = 180o − 110o, DCP, DCP = 70o

Page 150 :
148, , 145, , CHAPTER -- 13, Chapter, 13, , Surface Areas, Areas and, and Volumes, Volumes, Surface, Key Points :, , ●, ●, ●, ●, ●, ●, ●, ●, ●, ●, ●, ●, ●, ●, ●, ●, ●, ●, , Solids : Objects which occupy space in three dimensions., Edges : The line along which surface meet, Surface area : the area of the faces of a solid is called surface area., Volume : Measure of the space occupied by a solid., Cuboid : The solid which having lateral faces congruent and top and base are congruent., l, Lateral surface area of cuboid = LSA = 2h(l+b), l l, Total surface area of cuboid = TSA = 2(lh+lb+bh), Volume of a cuboid = V = length x breadth x height = llbh, Cube : In a solid all the faces are congruent, Lateral surface area of cube = LSA = 4a2, Total surface area of cube = TSA = 6a2, Volume of cube = v = a3, Cylinder : If a rectangle revolves about one of its sides and completes a full rotation, the solid, formed.is called Cylinder., Lateral surface area of cylinder = LSA = 2prh, Total surface area of cylinder = TSA = 2pr(r+h), Volume of a cylinder = V = pr2h, Cone : If a right angles triangle is revolved about one of the side containing the right angle, the, solid formed is called right circular cone., Lateral surface area cone = LSA = prll, Slant height = l2 = r 2 + h 2 \ l =, , ●, ●, ●, ●, ●, ●, ●, ●, ●, , r2 + h2, , Total surface area cone = TSA = pr(r+l), l, Volume of cone = V = 1/3 pr2h, Sphere : If a circular disc is rotated about one of its diameters, the solid generated is called, sphere., Surface area of sphere = LSA = TSA = 4pr2, Volume of a sphere = V = 4/3 pr3, Hemisphere : If sphere is divided into two equal parts each part is called hemisphere., Lateral surface area of hemisphere = LSA = 2pr2., Total surface area of hemisphere = TSA = 3pr2., Volume of hemisphere = V = 2/3 pr3.

Page 151 :
149, IX Standard – Mathematics, , Chapter 13 – Surface Areas and Volumes, , 146, , Exercise 13.1, , 1., , A plastic box 1.5 m long, 1.25 m wide and, 65 cm deep is to be made. It is opened at the, top. Ignoring the thickness of the plastic, sheet, determine:, (i) The area of the sheet required for, making the box., (ii) The cost of sheet for it, if a sheet, measuring lm2 costs Rs 20., Ans. l = 1.5m, b = 1.25m & h = 65cm = 0.65m., Sheet required for making box top opened, = area of base + LSA, =, lb + 2h(l + b), , is Rs 15000, find the height of the hall., [Hint: Area of the four walls = Lateral, surface area.], Ans. Let the length, breadth and height of the, rectangular hall be l,b & h., Perimeter of rectangular hall = 250, 2 (l + b ) =, 250, 250, = 125, 2, Cost of painting the four walls at the rate, , l + b=, , of Rs10 per m 2 is Rs15000, Area of four walls, = LSA, =, , = 1.5 × 1.25 + 2 × 0.65 (1.5 + 1.25 ), , 2 (l + b) h =, 1500, , = 1.875 + 1.30 ( 2.75 ), , 2 (125 ) h = 1500, , = 1.875 + 3.575, = 5.450, , 1500, = 6, 250, h = 6m, , h, =, , = 5.45m 2, Cost of sheet1m 2 is 20Rs, = 5.45 × 20, = 109.00, = Rs109, , Hence , the height of the hallis 6m, 4., , 2., , The length, breadth and height of a, room are 5 m, 4 m and 3 m respectively., Find the cost of white washing the walls, of the room and the ceiling at the rate of, Rs 7.50 perm2., Ans. l = 5m, b = 4m and h = 3m, Area of white washing, = area of 4 walls + area of the celling, = 2h(l + b) + lb, = 2 × 3(5 + 4) + 5 × 4, = 6 × 9 + 20, = 54 + 20, , The paint in a certain container is, sufficient to paint an area equal to 9.375, m2. How many bricks of dimensions, 22.5 cm x 10 cm x 7.5 cm can be painted, out of this container?, Ans. Dimensions of brick. l = 22.5 cm, b = 10, cm and h = 7.5 cm., Total surface area of brick = 2(lb + bh + lh), = 2 ( 22.5 × 10 + 10 × 7.5 + 7.5 × 22.5 ), = 2 ( 225 + 75 + 168.75 ), = 2 ( 468.75 ), = 937.5cm 2, 937.5, = 0.09375m 2, 100 × 100, Number of bricks, Total area paint sufficient, =, Area of brick, 9.375, =, 0.09375, = 100, \ Number of bricks can be painted is100, , =, , 74m 2, Cost of white washing Rs 7.50 per m 2, =, 74 × 7.50 =, Rs 555, 3., , 15000, 10, , The floor of a rectangular hall has a, perimeter 250 m. If the cost of painting, the four walls at the rate of Rs 10 per m2

Page 152 :
Chapter, 150 13 – Surface Areas and Volumes, A cubical box has each edge 10 cm and, another cuboidal box is 12.5 cm long, 10, cm wide and 8 cm high., (i) Which box has the greater lateral, surface area and by how much?, (ii) Which box has the smaller total, surface area and by how much?, Ans. i. Cubical box edge = a = 10 cm, Lateral surface area = 4a2 = 4(10)2, =4 x 100 = 400 cm2, For cubical box l = 12.5 cm, b = 10 cm &, h = 8 cm., \Lateral surface cuboidal box, =2h(l + b), = 2 x 8 (12.5 + 10), = 16 x 22.5, = 360 cm2, Cubical box has greater lateral surface area, than the cuboidal box by (400-360)cm2, i.e., 40cm2, ii. Total surface area of cubical box = 6a2, = 6(10)2 = 6 x 100, = 600 cm2, Total surface area of cuboidal box, = 2(lb + bh + lh), = 2[(12.5)(10) + (10)(8) + (8)(12.5)], = 2[125 + 80 + 100], = 2[305], = 610 cm2, Cubical box has the smaller total surface, area than the cuboidal box by (610-600), cm2 i.e., 10 cm2., , IX Standard – Mathematics, 147, , 5., , 6., , ii. The tape need for all the 12 edges, = 4(l + b + h), = 4(30 + 25 + 25), = 4 x 80 = 320 cm, 7., , Shanti Sweets Stall was placing an, order for making cardboard boxes for, packing their sweets. Two sizes of boxes, were required. The bigger of dimensions, 25 cm x 20 cm x 5 cm and the smaller of, dimensions 15 cm x 12 cm x 5 cm. For, all the overlaps, 5% of the total surface, area is required extra. If the cost of the, cardboard is Rs 4 for 1000 cm2, find the, cost of cardboard required for supplying, 250 boxes of each kind., Ans. For bigger box l = 25 cm, b = 20cm & h, = 5cm, TSA of bigger box = 2(lb + bh + lh), = 2[(25)(20) + (20)(5) + 5(25)], = 2[500 + 100 + 125], = 2(725) = 1450 cm2, For smaller box l = 15 cm, b = 12 cm & h, = 5 cm, Total surface area = 2(lb + bh + lh), = 2(15 x 12 + 12 x 5 + 5 x 15), = 2(180 + 60 +75), = 2(315), = 630 cm2, Total card board required for 2 boxs of, smaller and bigger = 1450 +630=2080 cm2, Cardboard required all over laps 5%, 5, = 2080 ×, 100, 2, = 104 cm, Net surface area of both boxs, = 2080 + 104, = 2184, Net surface area of 250 boxs, = 2184 × 250, , A small indoor greenhouse (herbarium), is made entirely of glass panes (including, base) held together with tape. It is 30 cm, long, 25 cm wide and 25 cm high., (i) What is the area of the glass?, (ii) How much of tape is needed for all, the 12 edges?, Ans. For indoor green house, l = 30cm, b = 25cm and h = 25cm, = 5, 46, 000 cm 2, Area of glass = 2(lb + bh + lh), =2(30 x 25 + 25 x 25 + 25 x 30), Cost of cardboard Rs4 for1000cm 2, = 2(750 + 625 + 750), 5, 46, 000, = 2(2125), =, =, × 4 2184 Rs, 1000, = 4250 cm2

Page 153 :
151, IX Standard – Mathematics, , Chapter, 148 13 – Surface Areas and Volumes, 8., , Parveen wanted to make a temporary, shelter for her car, by making a box-like, structure with tarpaulin that covers all, the four sides and the top of the car (with, the front face as a flap which can be, rolled up). Assuming that the stitching, margins are very small, and therefore, negligible, how much tarpaulin would, be required to make the shelter of height, 2.5 m, with base dimensions 4 m x 3 m?, Ans. For shelter l = 4m, b = 3m and h = 2.5m, TSA of shelter = lb + 2h(l + b), = 4 x 3 + 2 x 2.5(4 + 3), = 12 + 5 x 7, = 12 + 35, = 47 m2, Hence 47m2 of trapaulin is required, Exercise 13.2, , The curved surface area of a right, circular cylinder of height 14 cm is 88, cm2. Find the diameter of the base of the, cylinder., Ans. Let radius = r = ?, h = 14 cm and, LSA = 88 cm2 , d = ?, LSA of cylinder = 2prh, 22, 88 = 2 × × r × 14, 7, = 44 × 2r, 88, 88 = 88r, 88, =, r = 1cm, 88, d = 2r = 2 ×1 = 2 cm, Diameter of the cylinder = 2 cm, , 140, =, = 0.7m, r d= = 70 cm, 2, 2, TSA of cylinder =p, 2 r (r + h), 22, × 0.7 ( 0.7 + 1), 7, = 44 × 0.1(1.7 ), =2 ×, , = 4.4 × 1.7, = 7.48 m 2, \ 7.48m 2 sheet is required, 3., , A metal pipe is 77 cm long. The inner, diameter of a cross section is 4 cm, the, outer diameter being 4.4 cm (see Fig., 13.11). Find its, (i) inner curved surface area,, (ii) outer curved surface area,, (iii) total surface area., , 1., , 2., , It is required to make a closed cylindrical, tank of height 1 m and base diameter, 140 cm from a metal sheet. How many, square metres of the sheet are required, for the same?, Ans. Given : h = 1m, d = 140 cm, 140, =, = 0.7m, r d= = 70 cm, 2, 2, TSA of cylinder =p, 2 r (r + h), 22, × 0.7 ( 0.7 + 1), 7, = 44 × 0.1(1.7 ), =2 ×, , Ans. Given h = 77 cm, inner diameter = d = 4cm, =, r d= 4= 2 cm, outer diameter, 2, 2, = D= 4.4 cm, 4.4, =, R D= = 2.2 cm, 2, 2, i.Inner curved surface area = 2prh, 22, = 2 × × 2 × 77, 7, = 968cm 2, ii.Outer curved surface area = 2pRh, 22, =2 × × 2.2 × 77, 7, = 48.4 × 22, = 1064.8cm 2, iii.Totalsurface area, , = 2pRh + 2prh + 2p ( R 2 − r 2 ), = 1064.8 + 968 + 2 ×, , = 1064.8 + 96 +, , 44, , 22 , 2, ( 2.2 ) − 22 , 7 , , × ( 4.84 − 4 )

Page 154 :
= 1064.8cm, iii.Totalsurface area, , = 2pRh + 2prh + 2p ( R 2 − r 2 ), , 22, 2, 152= 1064., Chapter, 13 – Surface Areas, and, Volumes, 8 + 968 + 2 × ( 2.2 ) − 22 , , 7 , = 1064.8 + 96 +, , 44, × ( 4.84 − 4 ), 7, , 44, × 0.84, 7, = 2032.8 + 5.28, = 2032.8 +, , = 2038.08cm 2, 4., , The diameter of a roller is 84 cm and its, length is 120 cm. It takes 500 complete, revolutions to move once over to level, a playground. Find the area of the, playground in m2., Ans. Given d = 84 cm, 84, r d= = 42cm &=, h 120cm, =, 2 2, Area of the play ground leveled, = 2prh, in1complete revolution, 22, =2 × × 42 × 120, 7, = 31680cm 2, Area of the play ground leveled, = 31680 × 500, in 500 revolutions, = 15840000cm 2, 15840000 2, m, =, 100 × 100, = 1584 m 2, , A cylindrical pillar is 50 cm in diameter, and 3.5 m in height. Find the cost of, painting the curved surface of the pillar, at the rate of Rs12.50 per m2., Ans. d = 50cm, r d= 25cm, h 3.5m, =, = 0.25m &=, 2, Curved surface area of a piller = 2prh, 22, =2 × × 0.25 × 0.5, 7, = 5.5 m 2, Cost of painting the CSA of the piller at the, , IX Standard – Mathematics, 149, cylinder is 4.4 m2. If the radius of the, base of the cylinder is 0.7 m, find its, height., Ans. Let the height of the right circular cylinder, be ‘h’ m and r = 0.7m, Curved surface area = 4.4m2, 2prh =, 4.4, 22, 2 × × ( 0.7 ) × h =, 4.4, 7, 4.4h = 4.4, 4.4, =, h = 1m, 4.4, height of right circular cylinder is1m., 7., , The inner diameter of a circular well is, 3.5 m. It is 10 m deep. Find, (i) its inner curved surface area,, (ii) the cost of plastering this curved, surface at the rate of Rs 40 per m2., Ans. d = 3.5m and h = 10m., =, r d= 1.75 m, 2, inner curved surface area= 2prh, 22, =2 × × 1.75 × 10, 7, = 44 × 3.5, = 110m 2, ii.Cost of plastering the curved surface area, , 5., , 2, rate of Rs12.50 per m=, 5.5 × 12.50, = Rs 68.75, , 6., , Curved surface area of a right circular, , at rate of Rs40 per m 2 =40 × 110 =Rs 4400, 8., , In a hot water heating system, there is, a cylindrical pipe of length 28 m and, diameter 5 cm. Find the total radiating, surface in the system., Ans. h = 28 m, d = 5 cm,, =, =, r d= 5= 2.5cm,, r 0.025m, 2, 2, Total radiating surface= 2prh, 22, =2 × × 0.025 × 28, 7, = 44 × 0.100, = 4.4 m23, Total radiating surface is 4.4 m 2

Page 155 :
Cloth requied =p, 2 r ( h + 2.5 + 2.5 ), 22, × 10 ( 30 + 5 ), 7, 153, 22 IX Standard – Mathematics, =2 × × 10 × 35, 7, = 44 × 50, =2 ×, , Chapter, 150 13 – Surface Areas and Volumes, 9., , Find, (i) The lateral or curved surface area of, a closed cylindrical petrol storage tank, that is 4.2 m in diameter and 4.5 m high., ii. How much steel was actually used ,, if 1/12 of the steel actually used was, wasted in making the tank., Ans. d = 4.2m , r = 2.1m and h = 4.5 m, i. Lateral or curved surface area = 2prh, 22, =2 × × 2.1× 4.5, 7, = 9.0 × 6.6, = 59.4m 2, ii.Totalsurface area =p, 2 r (r + h), 22, × 2.1( 2.1 + 4.5 ), 7, = 44 × 0.3 × 6.6, =2 ×, , = 87.12m 2, Let the actual area of steel used be x m3 in, th, , 1, steel used was wasted., 12, x1 11, \x1 − = x, 12 12, 11, Actualsteel used x = 87.12, 12, 87.12, x, =, × 12, = 95.04m 2, 11, , In Fig. 13.12, you see the frame of a, lampshade. It is to be covered with a, decorative cloth. The frame has a base, diameter of 20 cm and height of 30 cm., A margin of 2.5 cm is to be given for, folding it over the top and bottom of the, frame. Find how much cloth is required, for covering the lampshade., Ans. d = 20cm, r = 10cm, h = 30 + 2.5 + 2.5, h = 35 cm, Cloth requied =p, 2 r ( h + 2.5 + 2.5 ), , = 2200 cm 2, 11., , The students of a Vidyalaya were, asked to participate in a competition, for making and decorating penholders, in the shape of a cylinder with a base,, using cardboard. Each penholder, was to be of radius 3 cm and height, 10.5 cm. The Vidyalaya was to supply, the competitors with cardboard. If, there were 35 competitors, how much, cardboard was required to be bought, for the competition?, Ans. r = 3 cm, h = 10.5 cm, Cardboard required for 1 competitor, = 2prh + pr 2, 22, 22, 2, = 2 × × 3 × 10.5 + × ( 3), 7, 7, 22 × 9, = 44 × 4.5 ×, 7, 198, = 198 +, 7,  1, = 198 1 + ,  7, 8 198 × 8 2, cm, = 198 × =, 7, 7, titors, \ Cardboard required for 35competitrs, =, , 10., , 22, × 10 ( 30 + 5 ), 7, 22, =2 × × 10 × 35, 7, = 44 × 50, =2 ×, , = 2200 cm 2, , 198 × 8, 35 7920 cm 2, ×=, 7, , Hence, 7920 cm2 of card board was, required to be bought for the competition., Exercise 13.3, , 1., , Diameter of the base of a cone is 10.5, cm and its slant height is 10 cm. Find its, curved surface area., Ans. d = 10.5 cm, 10.5, =, r = 5.25cm=, & l 10 cm, 2, \ Curved surface area of the cone =, pr1l, 22, = × 5.25 × 10, 7, = 165cm 2

Page 156 :
2, l=, r2 + h2, IX Standard – Mathematics, 151, 2, 2, l = r 2 + h 2 = ( 24 ) + (10 ), , 154 13 – Surface Areas and Volumes, Chapter, 2., , Find the total surface area of a cone, if, its slant height is 21 m and diameter of, its base is 24 m., Ans. l = 21m, d = 24m,, 24, =, r = 12 cm, 2, pr ( r + l ), Totalsurface area of cone =, , l, =, , l = 676, l = 26 m, Hence, the slant height of the tent is 26m, ii.CSA of tent = prl, 22, =, × 26 × 24, 7, Cost of canvas required to make the tent,, , 22, = × 12 ( 21 + 12 ), 7, 8712, = = 1244.57 cm 2, 7, , Curved surface area of a cone is 308 cm2, and its slant height is 14 cm. Find (i), radius of the base and (ii) total surface, area of the cone., Ans. CSA = 308 cm2 , l = 14 cm, i.CSA = prl, 22, 308=, × r × 14, 7, 308 = 44r, 308, r = 7 cm, =, 44, r = 7 cm, Radius of the base is 7cm, , if the cost of 1m 2 is, 22, Rs 70 =, × 26 × 24 × 70 = Rs137280, 7, Hence, the cost of the canvas is Rs 137280., , 3., , 5., , What length of tarpaulin 3 m wide will, be required to make conical tent of, height 8 m and base radius 6 m? Assume, that the extra length of material that, will be required for stitching margins, and wastage in cutting is approximately, 20 cm (Use p = 3.14)., Ans. h = 8m, r = 6m, l=, , (8), , 2, , + (6), , =, , = 462 cm 2, , = 188.4m 2, Width of tarpaulin = 3m, , 22, × 7 ( 7 + 14 ), 7, = 22 × 21, Totalsurface area of cone 462 cm 2, 4., , A conical tent is 10 m high and the, radius of its base is 24 m. Find, (i) slant height of the tent., (ii) cost of the canvas required to make, the tent, if the cost of 1 m2 canvas is Rs, 70., Ans. i. h = 10m , r = 24 m & l = ?, 2, l=, r2 + h2, , =, l, , h2 + r2 =, , l = 64 + 36 = 100, l =10m, Curved surface area = prl, = 3.14 × 6 × 10, , ii.Totalsurface area =, pr ( r + l ), , l=, , 576 + 100, , r2 + h2 =, , ( 24 ), , 2, , + (10 ), , 2, , 576 + 100, , l = 676, l = 26 m, Hence, the slant height of the tent is 26m, , 2, , 188.4, \ Length of tarpaulin =, = 62.8 m, 3, Extra length of the material required, cm 0.2 m, = 20, =, \ Actual length of tarpaulin required, = 62.8 + 0.2 = 63m, 6., , The slant height and base diameter, of a conical tomb are 25 m and 14 m, respectively. Find the cost of whitewashing its curved surface at the rate of, Rs 210 per 100 m2.

Page 157 :
=, l, , Chapter, 152 13 – Surface Areas and Volumes, , =, l, , Ans. l = 25m, d = 14m,, 14, =, r = 7m, 2, Curved surface area of the tomb = pr1, 22, =, × 7 × 25, 7, = 550 m 2, Cost of white − washing the CSA of the, tomb at the rate of Rs 210 per100 m 2, 210, =, × 550, 100, = Rs1155, 7., , A joker’s cap is in the form of a right, circular cone of base radius 7 cm and, height 24 cm. Find the area of the sheet, required to make 10 such caps., Ans. r = 7cm, h = 24 cm, l=, , r2 + h2 =, , =, l, , 576 + 49, , ( 24 ), , 2, , + (7), , 2, , =, l =, 625 25cm, CSA of a cap = prl, 22, =, × 7 × 25, 7, = 550 cm 2, The area of the sheet required to make, 10such a caps = 550 × 10 = 5500 cm 2, 8., , A bus stop is barricaded from the, remaining part of the road, by using, 50 hollow cones made of recycled, cardboard. Each cone has a base, diameter of 40 cm and height 1 m. If the, outer side of each of the cones is to be, painted and the cost of painting is Rs 12, per m2, what will be the cost of painting, all these cones?, Ans. d = 40cm, r = 20 cm, r = 0.2m and h = 1m, =, l, =, l, , h2 + r2, , (1), , 2, , + ( 0.2 ), , 2, , l =1 + 0.04 =1.04, l =1.02m, Curved surface area = prl, 22, , h2 + r2, IX Standard, – Mathematics, 155, 2, 2, (1) + ( 0.2 ), , l =1 + 0.04 =1.04, l =1.02m, Curved surface area = prll, 22, =, × 0.2 × 1.02, 7, = 0.64056 m 2, \ Curved surface area of 50 cones, 50 32.028m 2, = 0.64056 ×=, \ Cost of painting all these cones, = 32.028 × 12, = 384.336Rs, = Rs 384.34, Exercise 13.4, , 1., , Find the surface area of a sphere of, radius:, (i) 10.5 cm (ii) 5.6 cm, (iii) 14 cm, Ans. i. r = 10.5 cm, Surface area of shpere, = 4pr 2, 22, 2, =4 × × (10.5 ), 7, 22, =4 × × 10.5 × 10.5, 7, = 1386 cm 2, ii.r = 5.6 cm, Surface area= 4pr 2, 22, 2, =4 × × ( 5.6 ), 7, 22, =4 × × 5.6 × 5.6, 7, = 394.24 cm 2, iii.r = 14 cm, Surface area= 4pr 2, 22, 2, =4 × × (14 ), 7, 22, =4 × × 14 × 14, 7, = 88 × 28, = 2464 cm 2

Page 158 :
IX Standard – Mathematics, 153, , Chapter, 156 13 – Surface Areas and Volumes, 2., , Find the surface area of a sphere of, diameter:, (i) 14 cm (ii) 21cm, (iii) 3.5 m, Ans. i. d = 14 cm, r = 7 cm, Surface are= 4pr 2, 22, 2, =4 × × ( 7 ), 7, 22, = 4× × 7× 7, 7, = 616 cm 2, =, =r 10.5cm, ii.d 21cm,, Surface area= 4pr 2, 22, 2, =4 × × (10.5 ), 7, 22, =4 × × 10.5 × 10.5, 7, = 1386 cm 2, =, =r 1.75cm, iii.d 3.5cm,, Surface area = 4pr 2, 22, =4 × × (1.75 ), 7, 22, =4 × × 1.75 × 1.75, 7, = 38.5cm 2, 3., , Find the total surface area of a, hemisphere of radius 10 cm. (Use p =, 3.14), Ans. r = 10cm, TSA = ?, TSA of hemisphere = 3pr 2, 22, 2, =3 × × (10 ), 7, 3 × 3.14 × 100, =, = 942 cm 2, 4., , The radius of a spherical balloon, increases from 7 cm to 14 cm as air is, being pumped into it. Find the ratio of, surface areas of the balloon in the two, cases., Ans. i. r = 7 cm, , Surface area = 4pr 2, 22, 2, =4 × × ( 7 ), 7, 22, =4 × × 49, 7, = 616 cm 2, Case ( ii ) r =14cm, Surface area= 4pr 2, 22, 2, =4 × × (14 ), 7, 22, =4 × × 14 × 14, 7, = 2464 cm 2, Ratio of surface area of ballon = 616:2464, = 1:4, 5., , A hemispherical bowl made of brass has, inner diameter 10.5 cm. Find the cost of, tin-plating it on the inside at the rate of, Rs 16 per 100 cm2., Ans. i. Inner diameter = 10.5 cm, r = 5.25 cm, Inner surface area= 2pr 2, 22, 2, =2 × × ( 5.25 ), 7, 22, =2 × × 5.25 × 5.25, 7, = 173.25cm 2, Cost of tin − plating at the rate of Rs16, per100 cm 2, 16, Rs 27.72, = × 173.25 =, 100, 6., , Find the radius of a sphere whose, surface area is 154 cm2., Ans. Surface area = 154cm2 and r = ?, Surface area = 4pr2, 4pr 2 =, 154, 154 154 7, =, r2, =, ×, 4p, 4 22, 49, r2 =, 4, 7, r=, cm, 2, r = 3.5cm, Radius of the sphere is 3.5cm

Page 159 :
4pr 2 =, 154, 154 154 7, =, =, ×, r2, 4p, 4 22, Chapter, 49 – Surface Areas and Volumes, 154r 2 = 13, 4, 7, r=, cm, 2, r = 3.5cm, Radius of the sphere is 3.5cm, The diameter of the moon is, approximately one fourth of the, diameter of the earth. Find the ratio of, their surface areas., Ans. Let the diameter of earth = d, d = 2r, r = r, Then the diameter of moon, 1, 1, r, earth, 2r, =, = =, 4, 4, 2, r, radius moon= r=, 4, Surface area of earth = 4pr 2 and, , 157, IX Standard – Mathematics, , 7., , ( 4), , Surface area of moon = 4p r, , 2, , 4pr 2 pr 2, =, 16, 4, Ratio of their surface area, Surface area of moon, =, Surface area of earth, 1 2, pr, = 4 2, 4pr, 1, = = 1:16, 16, , =, , 8., , A hemispherical bowl is made of steel,, 0.25 cm thick. The inner radius of the, bowl is 5 cm. Find the outer curved, surface area of the bowl., Ans. Inner radius of the bowl = 5cm & thickness, of steel = 0.25 cm, \Outer radius of the bowl = 5 + 0.25 =, 5.25 cm, \Outer curved surface of the bowl = 4pr2, 22, =4 × × ( 5.25 ), 346.5cm, , 9., , A right circular cylinder just encloses a, sphere of radius r (see Fig. 13.22). Find, , (i) surface area of the sphere,, (ii) curved surface area of the cylinder,, (iii) ratio of the areas obtained in (i) and (ii)., Ans. i. Surface area of sphere = 4pr2, ii. For cylinder radius = r & height = 2r, \Curved surface area of cylinder = 2prh, = 2p(r) (2r) = 4pr2, Ratio of area sphere to cylinder, 4pr 2 1, = =, 4pr 2 1, = 1:1, Exercise 13.5, , 1., , A matchbox measures 4 cm x 2.5 cm x, 1.5 cm. What will be the volume of a, packet containing 12 such boxes?, Ans. l = 4cm, b = 2.5 cm & h = 1.5 cm, Volume of matchbox =l × b × h, =4 × 2.5 × 1.5, = 15cm3, Volume of 12 match box= 15 × 12, = 180 cm3, 2., , A cuboidal water tank is 6 m long, 5 m, wide and 4.5 m deep. How many litres of, water can it hold?(lm3 = 1000 l), Ans. l = 6m, b = 5m & h = 4.5 m, Capacity of the tank = l x b x h, = 6 x 5 x 4.5, = 135 m3, Volume of water it can hold in litres, = 135 x 1000, = 135000 litres, 3., , A cuboidal vessel is 10 m long and 8 m, wide. How high must it be made to hold, 380 cubic metres of a liquid?, Ans. l = 10m, b = 8m, h = ? & V = 380 m3

Page 160 :
158 13 – Surface Areas and Volumes, Chapter, Capacity of the cuboidal vessel = 380m3, h = 380, 10 × 8 × h =380, 380 19, h =, =, 8 × 10 4, h = 4.75m, 4., , Find the cost of digging a cuboidal pit 8, m long, 6 m broad and 3 m deep at the, rate of Rs 30 perm3., Ans. l = 8m, b = 6m, h = 3m & V = ?, Volume of cuboidal pit = lbh, =8x6x3, = 144m3, Cost of digging the cuboidal pit Rs 30 per, m3 = 144 x 30 = Rs 4320., 5., , The capacity of a cuboidal tank is, 50000 litres of water. Find the breadth, of the tank, if its length and depth are, respectively 2.5 m and 10 m., Ans. l = 2.5m, h = 10m, b = ?, Capacity of the cuboidal tank = 50000, litres, 50000, = = 50 m3, 1000, lbh = 50 m3, 50, 50, =, b =, = 2m, lh 2.5 × 10, b = 2m, Breadth of cuboidal tank is 2m, A village, having a population of 4000,, requires 150 litres of water per head per, day. It has a tank measuring 20 m x 15, m x 6 m. For how many days will the, water of this tank last?, Ans. Requirement of water per head per day is, 150 litres., \Required water per 4000 persons, = 4000 x 150, = 600000 litres, Volume of water required per one day, 600000, = = 600 m3, 1000, For =, tank l 20m,, b 15m, & h 6m, =, =, Capacity of tank =l × b × h, = 20 × 15 × 6, = 20 × 90, , – Mathematics, 600000 IX Standard, 155, = 600 m3, 1000, For =, tank l 20m,, b 15m, & h 6m, =, =, , =, , Capacity of tank =l × b × h, = 20 × 15 × 6, = 20 × 90, = 1800 m3, Number of days water last, Capacity of tank, =, Volume of water per day, 1800, = = 3days, 600, Water of the tank will last 3 days., 7., , A godown measures 40 m x 25 m x, 15 m. Find the maximum number of, wooden crates each measuring 1.5mx, 1.25mx0.5m that can be stored in the, godown., Ans. For godown l = 40m, b = 25m & h = 15m, Capacity of godown = llbh, = 40 × 25 × 15, = 15000m3, For wooden crate, =l 1.5m,, =, b 1.25m, =, & h 0.5m, Capacity of wooden crate = lbh, =1.5 × 1.25 × 0.5, = 0.9375 m3, Number of wooden crates, Capacity of godown, =, Capacity of wooden crate, 15000, =, 0.9375, = 16000, 16000 wooden crates can be stored in godown., , 6., , 8., , A solid cube of side 12 cm is cut into, eight cubes of equal volume. What will, be the side of the new cube? Also, find, the ratio between their surface areas., Ans. Side of solid cube = a = 12 cm, Volume of solid cube = a3, = (12 ), , 3, , = 1728cm3, Then it cutted into8cubes of equal, 1728, volume of small cube, = = 216 cm3

Page 161 :
159, IX Standard – Mathematics, , 3, Chapter 13 –=Surface, Areas and Volumes, (12 ), , 156, , = 1728cm, , 3, , Exercise 13.6, , Then it cutted into8cubes of equal, 1728, volume of small cube, = = 216 cm3, 8, Volume of small cube = 216, , 1., , The circumference of the base of a, cylindrical vessel is 132 cm and its height, is 25 cm. How many litres of water can it, hold? (1000 cm3 = 1 litre), Ans. c = 132 cm, h = 25 cm, r = ? & v = ? ,, c = 2pr, 22, 132 =2 × × r, 7, 132 × 7, r=, 2 × 22, r = 21cm, \ Capacity of the cylinderical, , a 3 = 216, a = 3 216, a = 6 cm, Surface area of original cube = 6a 2, = 6 (12 ), , 2, , = 6 × 144, = 864 cm 2, Surface area of new=, cube 6=, (a ) 6 (6), 2, , 2, , = 6 × 36, = 216 cm 2, Ratio of their surface areas, Surface area of original cube, =, Surface area of new cube, 864 4, = =, 216 1, Ratio of their surface areas 4:1, 9., , A river 3 m deep and 40 m wide is, flowing at the rate of 2 km per hour., How much water will fall into the sea in, a minute?, Ans. In one hour, l = 2 km = 2 x 1000m = 2000m, b = 40m, & h = 3m, Water fell into sea in one hour = llbh, = 2000 × 40 × 3, = 240000 m3, Water fellinto sea in one minute, 2000 × 40 × 3 3, =, m, 60, = 4000 m3, 4000m3 of water will fallinto the sea, in a minute, , vessel = pr 2 h, 22, 2, = × ( 21) × 25, 7, = 34650 cm3, 34650, = = 34.65litres, 1000, Hence cylindrical vessel can hold 34.65, litres of water., 2., The inner diameter of a cylindrical, wooden pipe is 24 cm and its outer, diameter is 28 cm. The length of the pipe, is 35 cm. Find the mass of the pipe, if 1 cm3, of wood has aamass, massof, of0.6, 0.6g., g., Ans. Inner diameter = 24 cm, Outer diameter = 28 cm, 24, = 12 cm &, 2, 28, =, R = 14 cm, 2, h = 35cm, , =, r, , p (R 2 − r2 ) h, Thickness of pipe =, 22 , 2, 2, (14 ) − (12 )  × 35, , 7, 22 × 5 [196 − 144], =, , =, , = 110 × 52, = 5720 cm3, Mass of pipe1cm3 is 0.69, = 5720 × 0.6, = 3432 g, = 3.432 kg

Page 162 :
160 13 – Surface Areas and Volumes, Chapter, 3., , A soft drink is available in two packs (i) a tin can with a rectangular base of, length 5 cm and width 4 cm, having a, height of 15 cm and (ii) a plastic cylinder, with circular base of diameter 7 cm, and height 10 cm. Which container has, greater capacity and by how much?, Ans. For tin can l = 5cm, b = 4cm & h = 15 cm, \ Capacity = l × b × h, = 5 × 4 × 15, = 300 cm3, ii.For plastic cylider, =, d 7=, cm, r 3.5cm, =, & h 10 cm, \ Capacity =, pr 2 h, 22, 2, = × ( 3.5 ) × 10, 7, 22, =, × 3.5 × 3.5 × 10, 7, = 385cm3, Plastic cylinder has greater capacity, , IX Standard – Mathematics, 157, per m2, find, (i) inner curved surface area of the, vessel,, (ii) radius of the base,, (iii) capacity of the vessel., Ans. i. Inner curved surface area of vessel, 2200, = = 110 m 2, 20, 2, =, =, =, ii.h 10m,, CSA 110m, &r ?, CSA = 2prh, 22, 2 × × r × 10 =110, 7, 110 × 7 7, =, r =, 44 × 10 4, =, r 1.75 m, =, =, =, iii.r 1.75m,, h 10m,, V ?, Capacity of a vessel = pr 2 h, 22, 2, =× (1.75 ) × 10, 7, 22, = × 1.75 × 1.75 × 10, 7, = 96.25 m3, Hence the capacity of the vesselis, , i.e., 385 − 300 =, 85cm3, 4., , If the lateral surface of a cylinder is 94.2, cm2 and its height is 5 cm, then find, (i) radius of its base, (ii) its volume. (Use p = 3.14), Ans. LSA = 94.2 cm2 & h = 5 cm, LSA of cylinder = 22prh, pth, 2prh =, 94.2, 2 × 3.14 × r × 5 =94.2, 94.2, r=, 2 × 3.14 × 5, r = 3cm, Volume of cylinder = pr 2 h, = 3.14 × ( 3) × 5, 2, , = 15.7 × 9, = 141.3cm3, 5., , It costs Rs 2200 to paint the inner curved, surface of a cylindrical vessel 10 m deep. If, the cost of painting is at the rate of Rs 20, , 96.25m3, , 6., , The capacity of a closed cylindrical, vessel of height 1 m is 15.4 litres. How, many square metres of metal sheet, would be needed to make it?, Ans. h = 1m, Capacity = 15.4 liters =, 15.4, Capacity, = 15.4, =, litres, 1000, = 0.0154m3, Let the radius of the base, & h 1m, = r=, 0.0154, pr 2 h =, 22 2, × r × 1 =0.0154, 7, 0.0154 × 7, r2 =, 22, r 2 0.0077 × 7, =, r 2 = 0.0049, r = 0.0049, r = 0.07 m

Page 163 :
22 2, × r × 1 =0.0154, 7, 0.0154 × 7, r2 =, Chapter 13 –22Surface Areas and Volumes, 158 2, r, 0.0077 × 7, =, , 161, IX Standard – Mathematics, 8., , r 2 = 0.0049, r = 0.0049, r = 0.07 m, Totalsurface area =2pr ( r + h ), 22, × 0.07 (1 + 0.07 ), 7, =44 × 0.01× 1.07, =2 ×, , A patient in a hospital is given soup daily, in a cylindrical bowl of diameter 7 cm. If, the bowl is filled with soup to a height of, 4 cm, how much soup the hospital has to, prepare daily to serve 250 patients?, Ans. d = 7 cm, r 7=, & h 4 cm, =, 2, \ Volume of soup in the cylindrical bowl, = pr 2 h, 2, 22, =× 7, ×4, 2, 7, 2 49, = × ×4, 7 4, = 22 × 7, , = 0.4708m 2, A lead pencil consists of a cylinder of, wood with a solid cylinder of graphite, filled in the interior. The diameter of the, pencil is 7 mm and the diameter of the, graphite is 1 mm. If the length of the, pencil is 14 cm, find the volume of the, wood and that of the graphite., Ans. Solid cylinder of graphite, d = 1mm, r = 1/2 mm, h = 14cm = 140 mm, Volume of the graphite = pr 2 h, 2, 22, =× 1, × 140, 2, 7, , ( ), , 7., , ( ), , = 110 mm, , 3, , 110, = = 0.11cm3, 10 × 10 × 10, For cylinder of wood, =, = 140 mm, d 7mm,\=, r 7 mm =, , h 14cm, 2, 2, p (R − r2 ) h, Volume of the wood =, 22  7   1 ,   −  , 7  2   2 , 2, , =, , 2, , , 140, , , 22  49 1 ,  −  × 140, 7  4 4, 22 48, =, × × 140, 7 4, = 5280 mm3, 5280, Volume of the wood =, 10 × 10 × 10, = 5.28cm3, =, , = 154 cm3, Volume of soup to be prepared daily, to serve 250 patients, = 154 × 250, = 38500 cm3, = 38.5liters, Exercise 13.7, , 1., , Find the volume of the right circular, cone with, (i) radius 6 cm, height 7 cm, (ii) radius 3.5 cm, height 12 cm, Ans. r = 6 cm & h = 7 cm, , = 1 pr 2 h, Volume of right circular cone, 3, 22, 2, = 1 × × (6) × 7, 3 7, 22, = 1 × × 36 × 7, 3 7, = 264 cm3, =, =, ii.r 3.5cm, and h 12cm, = 1 pr 2 h, Volume of right circular cone, 3, 22, 2, = 1 × × ( 3.5 ) × 12, 3 7, 1 22, = × × 3.5 × 3.5 × 12, 3 7, = 22 × 2 × 3.5, = 44 × 3.5, = 154 cm3

Page 164 :
Volume of cone, = 1 pr 2 h, 3, 1 × 3.14 × r 2 × 15 =, 1570 – Mathematics, IX Standard, 3, 159, , 162 13 – Surface Areas and Volumes, Chapter, , 3.14 × 5 × r 2 =, 1570, , 2., , Find the capacity in litres of a conical, vessel with, (i) radius 7 cm, slant height 25 cm, (ii) height 12 cm, slant height 13 cm, Ans. r = 7 cm, l = 25 cm, 2, l=, r2 + h2, h=, , ( 25) − ( 7 ), 2, , l −r =, 2, , 2, , r = 100, r = 10 cm, , 2, , 625 − 49, , =, , 15.7r 2 = 1570, 1570, r2 =, 15.7, r 2 = 100, , 4., , =, 484 22 cm, = 1 pr 2 h, Capacity of vessel, 3, 22, 2, = 1 × × ( 7 ) × 24, 3 7, 22, = 1 × × 49 × 24, 3 7, = 22 × 56, =, , = 1232 cm3 (1000cm3 = 1lts ), , If the volume of a right circular cone of, height 9 cm is 48 p cm3, find the diameter, of its base., Ans. h = 9cm, v=48p cm3 & d = ?, = 1 pr 2 h, Volume of right circular cone, 3, 2, 1, p, pr × 9, 48=, 3, 48p× 3, r2 =, 9p, r 2 = 16, =, r =, 16 4 cm, r = 4 cm, diameter = 2r = 2 × 4 = 8cm, , = 1.232 litres, =, ii.h 12=, cm & l 13cm, r=, , l2 − h 2 =, , r = 169 − 144 =, r = 5cm, , (13) − (12 ), 2, , 2, , 25, , = 1 pr 2 h, Capacity of conical vessel, 3, 22, 2, = 1 × × ( 5 ) × 12, 3 7, 2200 3, =, cm, 7, 2200, =, liters, 7000, 11, = litres, 35, 3., , The height of a cone is 15 cm. If its, volume is 1570 cm3, find the radius of, the base. (Use p = 3.14), Ans. h = 15cm, v = 1570cm3 and r = r, Volume of cone, = 1 pr 2 h, 3, 1 × 3.14 × r 2 × 15 =, 1570, 3, 2, 3.14 × 5 × r =, 1570, 15.7r 2 = 1570, 1570, r2 =, 15.7, , 5., , A conical pit of top diameter 3.5 m is 12, m deep. What is its capacity in kilolitres?, Ans. d = 3.5 m, 3.5, =, =, r = 1.75m,, h 12 m, 2, = 1 pr 2 h, Capacity of the conical pit, 3, 22, 2, = 1 × × (1.75 ) × 12, 3 7, 22, = 1 × × 1.75 × 1.75 × 12, 3 7, = 38.5m3, = 38.5 × 100 × 100 × 100, = 38500000 cm3, 38500000, = = 38500 liters, 1000, 38500, kilolitres, =, 1000, = 38.5 kll

Page 165 :
163, IX Standard – Mathematics, , Chapter, 160 13 – Surface Areas and Volumes, 6., , The volume of a right circular cone is, 9856 cm3. If the diameter of the base is, 28 cm, find, (i) height of the cone, (ii) slant height of the cone, (iii) curved surface area of the cone, Ans. V = 9856cm3 , d = 28 cm, 28, =, r = 14 cm, 2, i.Volume of cone, = 1 pr 2 h, 3, 22, 2, 9856 = 1 × × (14 ) × h, 3 7, , 22, 9856 = 1 × × 14 × 14 × h, 3 7, 9856 × 3, 44 × 14, h = 48cm, h=, , l=, , 2, , 2, , h +r =, , ( 48), , 2, , + (14 ), , is100pcm3, 8., , If the triangle ABC in the Question, 7 above is revolved about the side 5, cm, then find the volume of the solid, so obtained. Find also the ratio of the, volumes of the two solids obtained in, Questions 7 and 8., Ans. The solid obtained will be right circular, cone, whose radius of the base 12cm,, height = 5cm and slant height l = 13cm, 5cm, , height of the cone is 48cm, =, =, ii.r 14=, cm, h 48cm, &r ?, , 1 pr 2 h, \ Voluem of cone =, 3, 2, = 1 × p× ( 5 ) × (12 ), 3, = 1 × p× 25 × 12, 3, = 100pcm3, The volume of the solid so obtained, , 2, , Volume of cone, = 1 pr 2 h, 3, 2, = 1 × p× (12 ) × 5, 3, = 1 p× 12 × 12 × 5, 3, = 240pcm3, Ratio of the volumes of the two solids, obtained, = 100p :240=, p 5:12, , 22, × 14 × 50, 7, = 2200 cm 2, =, , 7., , A right triangle ABC with sides 5 cm, 12, cm and 13 cm is revolved about the side, 12 cm. Find the volume of the solid so, obtained., Ans. The solid obtained will be a right circular, cone whose radius of the base is 5cm,, height 12cm and slant height 13cm, cm, 13, 12cm, 5cm, , cm, , 12cm, , =, l, 2304 + 196= 2500, l = 50 cm, lHence,seant height of cone is 50cm, iii.r = 14cm, l = 50cm, Curved surface area = prll, , Hence, the curved surface area of the cone, is 2200cm2, , 13, , 9., , A heap of wheat is in the form of a cone, whose diameter is 10.5 m and height, is 3 m. Find its volume. The heap is, to be covered by canvas to protect it, from rain. Find the area of the canvas, required., Ans. Heap of wheat, 10.5, d 10.5m,, r = 5.25m,, h 3m, =, =, =, 2, = 1 pr 2 h, Volume, 3, 22, 2, = 1 × × ( 5.25 ) × 3, 3 7, Volume = 86.625m3, Slant height= l =, =, , ( 5.25), , r2 + h2, 2, , + ( 3), , 2

Page 166 :
2, 2, 1, Volume, =, pr h, 3, 22, 2, = 1 × × ( 5.25 ) × 3, 3, 7 Areas and Volumes, 164 13 – Surface, Chapter, Volume = 86.625m3, Slant height= l =, =, =, , ( 5.25), , IX Standard – Mathematics, 28, 161, = 14 cm, 2, 4 pr 3, \ Amount of water displaced =, 3, 22, 3, = 4 × × (14 ), 3 7, 22, = 4 × × 14 × 14 × 14, 3 7, 34496 3, =, cm, 3, 2, = 11498 cm3, 3, ii.Diameter = 0.21m, 0.21, r = 0.105 m, =, 2, 4 pr 3, \ Amount of water displaced =, 3, 22, 3, = 4 × × ( 0.105 ), 3 7, = 0.004851m3, r, =, , r2 + h2, 2, , + ( 3), , 2, , 27.5625 + 9, , = 36.5625, = 6.05 m, Curved surface area = prll, 22, = × 5.25 × 6.05, 7, = 99.825 m 2, Hence, the area of the canvas required, is 99.825 m 2, Exercise 13.8, , 1., , Find the volume of a sphere whose, radius is (i) 7 cm (ii) 0.63 m, Ans. r = 7 cm, = 4 pr 3, Volume, 3, 22, 3, = 4 × × (7), 3 7, 22, = 4 × ×7×7×7, 3 7, 4312 3, =, cm, 3, = 1437 1 cm3, 3, ii.r = 0.63m, = 4 pr 3, Volume, 3, 22, 3, = 4 × × ( 0.63), 3 7, 22, =4 × × 0.63 × 0.63 × 0.03, 3 7, = 1.05 m3, , 3., , The diameter of a metallic ball is 4.2, cm. What is the mass of the ball, if the, density of the metal is 8.9 g per cm3?, Ans. d = 4.2 cm, 4.2, =, r = 2.1cm, 2, 4 pr 3, \ Volume of ball =, 3, 22, 3, = 4 × × ( 2.1), 3 7, 22, = 4 × × 2.1× 2.1× 2.1, 3 7, = 38.808cm3, Density = 8.9gper cm3, \ Mass of the ball =, Volume × Density, = 38.808 × 8.9, = 345.39 g, , 4., The diameter of the moon is, Find the amount of water displaced by a, approximately one-fourth of the, solid spherical ball of diameter, diameter of the earth. What fraction of, (i) 28 cm (ii) 0.21m, the volume of the earth is the volume of, Ans. d = 28 cm, the moon?, 28, Ans., Radius of earth = r, diameter of earth = 2r, =, r = 14 cm, 2, 4 pr 3, \ Amount of water displaced =, 3, 22, 3, = 4 × × (14 ), 3 7, , 2.

Page 167 :
\ Outer radius ( R ), = Inner radius + thickness, = 1 + 0.01, = 1.01m IX Standard – Mathematics, 165, Volume of iron used the tank, = 2 p ( R 3 − r3 ), 3, 22, 3, 3, = 2 × × (1.01) − (1) , 3 7 , , 3, = 0.06348m, , Chapter, 162 13 – Surface Areas and Volumes, 1, 2r r, \ Diameter of moon =, =, ( 2r ) =, 2, 4, 4, r, Radius of moon = r × 1 =, 1, 2 4, 4 pr 3, Volume of the earth ( V=, 1), 3, 3, , 4 p r , Volume of the moon V=, 2, 3  4 , 1 4 3, =, Volume of moon,  pr , 64  3, , 1, Volume of moon =, volume of earth, 64, 1, Hence, the volume of the moon is th, 64, fraction of the volume of the earth., , How many litres of milk can a, hemispherical bowl of diameter 10.5 cm, hold?, Ans. d = 10.5 cm, 10.5, =, r = 5.25cm, 2, 2 pr 2, \ Amount of milk =, 3, 22, 3, = 2 × × ( 5.25 ), 3 7, 22, =2 × × 5.25 × 5.25 × 5.25, 3 7, = 303cm3, = 0.303litres, , 7., , Find the volume of a sphere whose, surface area is 154 cm2., Ans. Surface area = 154 cm2, 4pr 2 =, 154, 22, 4 × × r2 =, 154, 7, 154 × 7 49, r2 =, =, 22 × 4, 4, 49, r = 7 cm, =, 2, 4, 4 pr 3, \ Volume of sphere =, 3, 3, 22, 7, = 4 ×, 3 7, 2, , 5., , 6., , A hemispherical tank is made up of an, iron sheet 1 cm thick. If the inner radius, is 1 m, then find the volume of the iron, used to make the tank., Ans. Inner radius(r) = 1m & Thickness of iron, sheet = 1cm = 0.01m, \ Outer radius ( R ), = Inner radius + thickness, = 1 + 0.01, = 1.01m, Volume of iron used the tank, = 2 p ( R 3 − r3 ), 3, 22, 3, 3, = 2 × × (1.01) − (1) , 3 7 , , 3, , ( ), , 4 22 7 7 7, × × × ×, 3 7 2 2 2, 539 3, =, cm, 3, 2, = 179 cm3, 3, =, , 8., , A dome of a building is in the form of a, hemisphere. From inside, it was whitewashed at the cost of Rs 498.96. If the, cost of white-washing is Rs 2.00 per, square metre, find the, (i) inside surface area of the dome,, (ii) volume of the air inside the dome., Ans. i. In side surface area of the dome, 498.96, =, 2, = 249.48 m 2, ii.In side surface area = 249.48, 2pr 2 =, 249.48, 22 2, 2× × r =, 249.48, 7, 249.48 × 7, r2 =, 2 × 22, r 2 = 39.69, r = 39.69

Page 168 :
r2 = 3 27r1, , 2pr 2 =, 249.48, 22 2, 2× × r =, 249.48, 7, Chapter, – Surface, Areas and Volumes, 166 2 13, 249.48, ×7, r =, 2 × 22, r 2 = 39.69, r = 39.69, r = 6.3m, \ Volume of the air inside the done, = 2 pr 3, 3, 22, 3, = 2 × × ( 6.3), 3 7, 22, = 2 × × 6.3 × 6.3 × 6.3, 3 7, = 523.9 m3, 9., , Twenty seven solid iron spheres, each of, radius r and surface area S are melted to, form a sphere with surface area S’. Find, the (i) radius r’ of the new sphere,, (ii) ratio of S and S’., Ans. i. Volume of a solid iron sphere, = 4 pr13, 3, \ Volume of 27 solid iron spheres, , (, , ), , = 27 4 pr 3 = 36pr 3, 3, Volume of the new sphere= 36pr 3, Let the radius of the new sphere be r2 then, = 4 pr2, Volume of the new sphere, 3, According to the question, 4 3, pr2 = 36pr13, 3, ( 36pr13 ) 3, r23 =, 4p, 3, 3, r2 = ( 9r1 ) 3, r23 = 27r13, r2 = 3 27r13, r2 = 3 27r13, r2 = 3r1, \ Hence, the radius r2 of the, new sphere is 3r, ii.S12 = 4pr 2, S2 = 4p ( 3r1 ), , 2, , S=, 36pr12, 2, \, , S1, , =, , 4pr12, , = 1 = 1:9, , r2 = 3r1, \ Hence, the radius r2 of the, new sphereIX, is Standard, 3r, – Mathematics, 163, , ii.S2 = 4pr 2, , S12 = 4p ( 3r1 ), , 2, , 1, S=, 36pr12, 2, , \, , S1, 4pr12, = 1 = 1:9, 1 =, 9, S2 36pr12, , Hence, the ratio of S1 and S21 is1:9, 10., , A capsule of medicine is in the shape of, a sphere of diameter 3.5 mm. How much, medicine (in mm3) is needed to fill this, capsule?, Ans. d = 3.5 mm, 3.5, =, r = 1.75 mm, 2, 4 pr 3, \ Capacity of the capsule =, 3, 22, 3, = 4 × × (1.75 ), 3 7, = 22.46 mm3, Hence, 22.46 mm3 of medicine is needed, to fill this capsule., Exercise 13.9 (Optional), , 1., , A wooden bookshelf has external, dimensions as follows: Height =110 cm,, Depth = 25 cm, Breadth = 85 cm (see, Fig. 13.31). The thickness of the plank is, 5 cm everywhere. The external faces are, to be polished and the inner faces are to, be painted. If the rate of polishing is 20, paise per cm2 and the rate of painting is, 10 paise per cm2, find the total expenses, required for polishing and painting the, surface of the bookshelf.

Page 169 :
Chapter, 164 13 – Surface Areas and Volumes, Ans. Surface area to be polished, = {(110 × 85 ) + 2 (110 × 25 ) + 2 ( 85 × 25 ), +2 (110 × 5 ) + 4 ( 75 × 5 )}, =, , ( 9350 + 5500 + 4250 + 1100 + 1500 ) cm 2, , = 21700 cm 2, \ Expenses required for polishing 20 paise, 2, , per=, cm, 21700 × 20 paise, 21700 × 20, = = Rs 4340, 100, Surface area to be painted, =  2 ( 20 × 90 ) + 6 ( 75 × 20 ) + ( 75 × 90 ) , = 3600 + 9000 + 6750, , 21, = 10.5cm, 167, IX2 Standard – Mathematics, Surface area of wooden sphere= 4pr 2, 22, 2, =4 × × (10.5 ), 7, 22, =4 × × 10.5 × 10.5, 7, = 1386 cm 2, Surface area of woden sphere painted, , =, d 21,=, r, , = 1386 − p (1.5 ), , 2, , 22, 2, × (1.5 ) = 1378.93, 7, \ Surface area of light wooden spheres, , = 1386 −, , = 1378.93, =, × 8 11031.44 cm 2, , \ Cost of painting silver at 25 paise per cm 2, = 11031.44 × 25paise, = 19350 cm 2, 11031.44 × 25, =, = Rs 2757.86, Expenses required for painting at10 paise, 100, per=, cm 2 19350 × 10 paise, For cylinder, 19350 × 10, =, =, r 1.5cm,, h 7cm, = Rs, = Rs1935, 100, prh, Surface area of cylinder support, spport = =22prh, Total expenses required for polishing, 22, = 2 × × 1.5 × 7 = 66 cm 2, = 4340 + 1935, and painting, 7, = Rs 6275, Surface area of 8cylindricalsupports, , 2., , = 66 × 8 = 525cm 2, The front compound wall of a house, is decorated by wooden spheres of, \ Cost of painting black at 5 paise per cm 2, diameter 21 cm, placed on small, = 528 × 5 paise, supports as shown in Fig 13.32. Eight, 528 × 5, such spheres are used for this purpose,= Rs, = Rs 26.40, and are to be painted silver. Each, 100, support is a cylinder of radius 1.5 cm, \ Cost of paint required =, 2757.86 + 26.40, and height 7 cm and is to be painted, = Rs 2784.26, black. Find the cost of paint required if, silver paint costs 25 paise per cm2 and 3., The diameter of a sphere is decreased by, black paint costs 5 paise per cm2., 25%. By what per cent does its curved, surface area decrease?, Ans. Let the radius of sphere be r/2 cm., r, = 2=, Then its diameter, r cm, 2, Curved surface area of the originalsphere, , ( ), , Ans. For wooden sphere, 21, =, d 21,=, r = 10.5cm, 2, Surface area of wooden sphere= 4pr 2, 22, 2, =4 × × (10.5 ), 7, 22, =4 × × 10.5 × 10.5, , ( ), , 4pr 2, =pr 2 cm 2, 2, 4, New diameter ( decreased ) of the sphere, , =4pr 2 =4p r, , 25, 100, r 3r, =r − = cm, 4 4, , = r−r, , 2, , =

Page 170 :
( ), , = 2= r cm, Then its diameter, 2, Curved surface area of the originalsphere, , ( ), , 2, 4pr 2, =4pr 2 =4p r, =, =pr 2 cm 2, 2, 4, 168 13 – Surface Areas and Volumes, Chapter, New diameter ( decreased ) of the sphere, , 25, 100, r 3r, =r − = cm, 4 4, \ Radius of the new sphere, , = r−r, ,  3r  3r, = 1=, cm., 2  4  8, \ New curved surface area of the sphere, , IX Standard – Mathematics, 165, 4., , Formula to find curved surface area of, cylinder if base radius r and height h is, a) prh, b) 2 prh c) 3 prh d) 2 pr(r+h), , 5., , Formula to find TSA of cylinder of bae r, and height h is, a) prh, b) 2 prh, c) 2 pr(r+h), d) pr2h2, , 6., , The relation between l,r and h for a, right circular cone is, a) l2 = r2 + h2, b) r2 = l2 + h2, 2, 2, 2, c) h = l + r, d) l = r2 + h2, , 7., , The total surface area of a sphere of, radius is, 2, b) 2 pr2 c) 3 pr, pr2, d) 4 pr2, a) pr2, , 8., , The total surface area of a hemisphere, of radius r is, b) 3 pr2 c) 2 pr2 d) 4 pr2, a) pr2, , 2, ,  3r , =4pr 2 =4p  , 8, 2, 9pr, =, cm 2, 16, Decrease in original curved surface, 9pr 2, 16, 16pr 2 − 19pr 2 7 pr 2, =, =, 16, 16, , area =pr 2 −, , 9., , Volume of cone of base radius r and, height, h is, 7 pr, \ Percentage of decrease =, × 100%, b) 1/3 pr2h, a) pr2h, 16, 2, c), 4/3, pr, h, d), 2 pr2h, pr 2, 10. Volume of a hemisphere of radius r is, 700% 175, = =, %, a) 2 pr 3, b) 4 pr 3, 16, 4, 3, 3, = 43.75%, c)4pr 2, d) 3pr 2, 2, , Additional Problems, , I., , Multiple Choice Questions, , 1., , Lateral surface area of a cuboid with, dimensions l,b,h is, a) 2(lb + bh + lh) - 2bh, b) 2(lb + bh + lh), c) 2(l+h)h, d) lbh, , 2., , If volume of a cube is 343cm3 then its, edge is, a) 7 cm, b) 14cm c) 49 cm d) 21 cm, , 3., , Diagonal of a cube is, , 6 cm. Then its, , later a surface area is, a) 6 6 cm 2, b) 36cm 2, c)12 cm 2, , d)8cm 2, , 11., , The ratio of the radius of the two sphere, is 2 : 3 the ratio of their volume is, a) 7 : 8, b) 8 : 27, c) 4 : 9, d) 2 : 3, , 12., , The diameter of sphere is d. Its volume is, a)1/ 3 pd 3, 4, c) pd 3, 3, , 13., , 14., , 1, pd 3, 24, 1, d) pd 3, 6, b), , The ratio of the volumes of two spheres, is 1 : 27 the ratio of their radii is, a) 1 : 3, b) 1 : 9 c) 3 : 1 d) 1 : 27, , The number of edges of a cube are, a) 6, b) 8, c) 12, d) 16, Ans. 1) c, 2) a, 3) d, 4) 6, 5) b, 6) a, 7) d, 8) b, 9) 6, 10) a, 11) b, 12) c, 13) a, 14) c

Page 171 :
169, IX Standard – Mathematics, , Chapter, 166 13 – Surface Areas and Volumes, Answer the following questions, , 1., , Find the volume of the largest right, circular cone that can be cut off from a, cube whose edge is 9cm., Ans. Height of cone = 9 cm, Radius = 9/2, 1, Volume of cone= pr 2 h, 3, 1 22 9 9, = × × × ×9, 3 7 2 2, = 190.93cm3, Find the volume of a sphere whose, diameter is 7cm., Ans. Diameter of sphere = 7 cm, Radius = 7 cm, 2, = 4 pr 3, Volume of sphere, 3, 22, 7 7 7, = 4 × × × ×, 3 7 2 2 2, 539 3, =, cm, 3, = 179.66 cm3, , 5., , The radius and height of cylinder are, in the ratio 2 : 3. If the volume of the, cylinder is 1617 cm3 , then find its radius, and height, Ans. r = 2x & h = 3x, Volume of cylinder = ( pr 2 h ), 1617 = p× ( 2x ) ( 3x ), 2, , 22, × 4 × 3 × x3, 7, 1617 × 7, 3, x =, 22 × 4, , 1617=, , ( 2), , x3 = 7, , 2., , 3., , The area of the base of a solid hemisphere, is 36cm2. Find the CSA., pr2 = 36cm2, Ans. Area of base =7p, CSA of hemishere = 2pr2, = 2 x 36, = 72 cm2, The side of a cube is 8cm. If it is cut into, smaller cubes of side 8cm, then find the, number of such cubes., Ans. Edge of cube = 8 cm., Volume of cube = a3 = (8)3, Edge of each small cube = a = 2, Volume of small cube = (a)3 = (2)3 = 8 cm3, \ Number of small cubes, Volume of big cube, =, Volume of small cube, 512, = = 64, 8, , 3, , x = 7 cm, 2, , Radius =, 2x =×, 2 7 =, 7 cm, 2, 21, Height =, 3x =×, 3 7 = cm, 2 2, Find the curved surface area, are and TSA of, a hemisphere of radius 35 cm, Ans. Radius of hemisphere = 35cm, \Curved surface area of hemisphere = 2 pr2, 22, 2, =2 × × ( 35 ), 7, = 7700 cm 2, 6., , Totalsurface area of hemisphere = 3pr 2, 22, =3 × × 35 × 35, 7, = 66 × 5 × 35, , 4., , = 11550 cm 2, 7., , Find the volume of the largest right, circular cone that can be placed in a, cube of edge 14 cm., Ans. r = 7cm & h = 14 cm, Volume of largest cone, = 1 pr 2 h, 3, 22, 2, = 1 × × ( 7 ) × 14, 3 7, 2156, = = 718 2 cm3, 3, 3

Page 172 :
167, , 170, , Chapter - 14, CHAPTER - 14, , Statistics, Statistics, , Key Points :, , ●, ●, ●, ●, ●, ●, ●, ●, ●, ●, ●, ●, ●, ●, ●, ●, ●, ●, ●, ●, ●, ●, ●, ●, , Statistics : Statistics may be defined as the science of collection, classification, analysis and, interpretation of numerical data., Data : The collection of all the observations (or) scores is called data, Raw data : A collection of observations gathered initially., Frequency distribution table : Representing data showing each score and the corresponding, number of repetitions or frequency., Frequency : The number of times a particular score repeats itself., Score : The numerical entries is an observation., Range : The difference between the highest and the lowest scores in an observation., Grouped frequency distribution : The data is collected in to several groups and the frequency, of scores in each group is recorded., Class interval : In a grouped frequency distribution each group is called a class interval., Cumulative frequency : The sum of the frequencies up to the current class interval., Frequency distribution table : It displays the frequency of scores corresponding to various, class intervals., Inclusive method : While grouping, the end points of the groups donot overlap., Exclusive method : The end points of consecutive groups overlap., Class limit : The end points of a class in exclusive method; the end points of a class with, correction factors in inclusive method., Class size : The difference between the upper class, case limit and the lower class limit., Class mark : The mid point of the class intervals. It is equal to the average between the upper, class limit and the lower class limit., Histogram : A graphical way of representing grouped data using rectangular bars in which the, frequency is proportional to the area of the rectangle., Mean : Average of the scores. It is equal to the sum of the scores divided by the number of, scores., Central tendency : The tendency of scores to cluster around a central value., Measures of central tendency are, i. Mean, ii. Median & iii. Mode, Median : The middle most score in an ordered distribution of scores, The number of given scores is odd then the middle most score is median, The number of given scores is even , take the average of the two middle scores as median., Mode : The most often repeated score in a given set of scores.

Page 173 :
171, IX Standard – Mathematics, , Chapter, 168 14 – Statistics, Exercise 14.1, , 1., , Give the examples of data that you can, collect from your day - to - day life., Ans. i. Number of subjects in 10th standard., ii. Number of switchs in the house., iii. Number of windows in the house., iv. Number of languages printed int the, currency notes., v. Election results obtained from television, or newspaper., , Ans., , Classify the data in Q.1 above as, primary or secondary data., Ans. (i), (ii) and (iii) are primary data (iv) and, (v) are secondary data., , Ans., , Blood, group, , Number of, students, (frequency), A, 1111 1111, 9, B, 1111 1, 6, AB, 111, 3, 0, 1111 1111 11, 12, O is the most common blood group and, AB is the rarest blood group among these, students., 2., , Tally marks, , The distance (in km) of 40 engineers from, their residence to their place of work were, found as follows:, 5, , 3, , 10, , 20, , 25, , 11, , 13, , 7, , 12, , 31, , 12, , 17, , 18, , 11, , 32, , 17, , 16, , 2, , 7, , 9, , 7, , 8, , 3, , 5, , 12, , 15, , 18, , 3, , 12, , 14, , 2, , 9, , 6, , 15, , 15, , 7, , 6, , 12, , Construct a grouped frequency, distribution table with class size 5 for, the data given above taking the first, interval as 0-5 (5 not included). What, main features do you observe from this, tabular representation?, Tally marks, , Number of, engineers, , 0-5, 1111, 5, 5 - 10, 1111 1111 1, 11, 10 - 15, 1111 1111 1, 11, 15 - 20, 1111 1111, 9, 20 - 25, 1, 1, 25 - 30, 1, 1, 30 - 35, 11, 2, i. Distance 10 - 15 & 5 - 10 maximum, number of engineers coming from, residence to work place., ii. Distance from 20 - 25 and 25 - 30, minimum number of engineers coming, from residence to work place., , Exercise 14.2, , The blood groups of 30 students of Class, VIII are recorded as follows:, A, B, O, O, AB, O, A, O, B, A, O, B, A,, O, O, A, AB, O, A, A, O, O, AB, B, A, O,, B, A, B, O., Represent this data in the form of a, frequency distribution table. Which, is the most common, and which is, the rarest, blood group among these, students?, , 10, , Distance(in, km), , 2., , 1., , 19, , 3., , The relative humidity (in %) of a, certain city for a month of 30 days was, as follows:, , 98.1 98.6 99.2 90.3 86.5 95.3 92.9 96.3, , 94.2 95.1, , 93.3, , 95.2 97.3, , 89.2 92.3 97.1 93.5 92.7 95.1 97.2, , 96.2 92.1 84.9 90.2 95.7 98.3 97.3 96.1, , 92.1, , 89, , (i) Construct a grouped frequency, distribution table with classes 84 - 86,, 86-88, etc., (ii) Which month or season do you think, this data is about?, (iii) What is the range of this data?, Ans. i.

Page 174 :
172 14 – Statistics, Chapter, , IX Standard – Mathematics, 169, , Relative, humidity, , Tally marks, , Number, of days, (frequency), , 84 - 86, , 1, , 1, , 86 - 88, , 1, , 1, , 88 - 90, , 11, , 2, , 90 - 92, , 11, , 2, , 92 - 94, , 1111 11, , 7, , 94 - 96, , 1111 1, , 6, , 96 - 98, , 1111 11, , 7, , 98 - 100, , 1111, , 4, , ii. The data is about rainy season as the, relative humidity is high., iii. Range = Highest score - Lowest + score, = 99.2 - 84.9 = 14.3%, 4., , The heights of 50 students, measured, to the nearest centimetres, have been, found to be as follows:, 161 150 154 165 168 161 154 162 150 151, , More than 50% of students are shorter than, 165 cm, 5., , A study was conducted to find out the, concentration of sulphur dioxide in, the air in parts per million (ppm) of a, certain city. The data obtained for 30, days is as follows:, 0.03 0.08 0.08 0.09 0.04 0.17, 0.16 0.05 0.02 0.06 0.18 0.20, 0.11 0.08 0.12 0.13 0.22 0.07, 0.08 0.01 0.10 0.06 0.09 0.18, 0.11 0.07 0.05 0.07 0.01 0.04, (i) Make a grouped frequency, distribution table for this data with, class intervals as 0.00 - 0.04,0.04 - 0.08,, and so on., (ii) For how many days, was the, concentration of sulphur dioxide more, than 0.11 parts per million?, Ans. i., , 153 159 161 170 162 165 166 168 165 164, , Concentration, of sulphur, dioxide, , 154 152 153 156 158 162 160 161 173 166, , 0.00 - 0.04, , 1111, , 4, , 161 159 162 167 168 159 158 153 154 159, , 0.04 - 0.08, , 1111 1111, , 9, , 0.08 - 0.12, , 1111 1111, , 9, , 0.12 - 0.16, , 11, , 2, , 0.16 - 0.20, , 1111, , 4, , 0.20 - 0.24, , 11, , 162 164 171 165 158 154 156 172 160 170, , (i) Represent the data given above by a, grouped frequency distribution table,, taking the class intervals as 160 -165,165, -170, etc., (ii) What can you conclude about their, heights from the table?, Ans. i., Heights, , Tally marks, , Number of, students, (Frequency), , 150-155, , 1111 1111 11, , 12, , 155 - 160, , 1111 1111, , 9, , 160 - 165, , 1111, 1111, , 165 - 170, , 1111 1111, , 10, , 170 - 175, , 1111, , 5, , 1111, , Total, , Number, of days, (Frequency), , 2, 30, , ii. Concentration of sulphur dioxide was, more than 0.11 parts per million for 2 + 4, + 2 = 8 days., 6., , 14, , ii. Maximum number students are in the, teh, group 160 - 165 and heights of minimum, number of student are in the group 170 - 175, , Tally marks, , Ans., , Three coins were tossed 30 times, simultaneously. Each time the number, of heads occurring was noted down as, follows:, 0 1 2 2 1 2 3 1 3 0, 1 3 1 1 2 2 0 1 2 1, 3 0 0 1 1 2 3 2 2 0, Prepare a frequency distribution table, for the data given above.

Page 175 :
173, IX Standard – Mathematics, , Chapter, 170 14 – Statistics, Number of Tally marks, heads, 0, 1111 1, 1, 1111 1111, 2, 1111 1111, 3, 1111, Total, , Frequency, 6, 10, 9, 5, 30, , The value of p upto 50 decimal places is, given below:, 3.14159265358979323846264338327950, 288419716939937510, (i) Make a frequency distribution of, the digits from 0 to 9 after the decimal, point., (ii) What are the most and the least, frequently occurring digits?, Ans. i., , Ans., , Number of, hours, 0-5, 5 - 10, , 7., , Digits, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, , Tallys, Frequency, 11, 2, 1111, 5, 1111, 5, 1111 111, 8, 1111, 4, 1111, 5, 1111, 4, 1111, 4, 1111, 5, 1111 111, 8, Total, 50, ii. The most frequently occuring digits are, 3 and 9 and last frequently occuring digit, is 0., 8., , Thirty children were asked about the, number of hours they watched TV, programmes in the previous week. The, results were found as follows:, 1 6 2, 10 3 4, 3 2 8, , 3 5 12 5 8 4 8, 12 2 8 15 1 17 6, 5 9 6 8 7 14 12, , (i) Make a grouped frequency, distribution table for this data, taking, class width 5 and one of the class, intervals as 5 - 10., (ii) How many children watched, television for 15 or more hours a week?, Tally marks, , Frequency, , 1111 1111, 10, 1111 1111, 13, 111, 10 - 15, 1111, 5, 15 - 20, 11, 2, Total, 30, ii. The children watched television for 15, or more hours a week is 2, 9., , Ans., , A company manufactures car batteries of, a particular type. The lives (in years) of 40, such batteries were recorded as follows:, 2.6 3.0 3.7 3.2 2.2 4.1 3.5 4.5, 3.5 2.3 3.2 3.4 3.8 3.2 4.6 3.7, 2.5 4.4 3.4 3.3 2.9 3.0 4.3 2.8, 3.5 3.2 3.9 3.2 3.2 3.1 3.7 3.4, 4.6 3.8 3.2 2.6 3.5 4.2 2.9 3.6, Construct a grouped frequency, distribution table for this data, using, class intervals of size 0.5 starting from, the interval 2-2.5., Lives, 2.0 - 2.5, 2.5 - 3.0, 3.0 - 3.5, , Tallys, 11, 1111 1, 1111 1111, 1111, 3.5 - 4.0, 1111 1111, 1, 4.0 - 4.5, 1111, 4.5 - 5.0, 111, Total, , Frequency, 2, 6, 14, 11, 4, 3, 40

Page 176 :
174 14 – Statistics, Chapter, , IX Standard – Mathematics, 171, , Exercise 14.3, , S.No., , Causes, , Female fatality rate (%), , 1., , Reproductive health conditions, , 31.8, , 2., , Neuropsychiatric conditions, , 25.4, , 3., 4., , Injuries, Cardiovascular conditions, , 12.4, 4.3, , 5., , Respiratory conditions, , 4.1, , 6. Other causes, 22.0, (i) Represent the information given above graphically., (ii) Which condition is the major cause of women’s ill health and death worldwide?, (iii) Try to find out, with the help of your teacher, any two factors which play a major role, in the cause in (ii) above being the major cause., , 0, , Other causes, , Respiratory conditions, , Cardiovascular conditions, , Injuries, , 36, 32, 28, 24, 20, 16, 12, 8, 4, , Neuropsychiatric conditions, , Y, , Female Fatality rate %, , Ans., , A survey conducted by an organisation for the cause of illness and death among the, women between the ages 15-44 (in years) worldwide, found the following figures (in %):, , Reproductive health conditions, , 1., , Causes, , X, , ii. Reproductive health conditions is the major cause of women’s ill health and death world, wide., iii. Lack of proper diet, lack of advised exercises., 2., , The following data on the number of girls (to the nearest ten) per thousand boys in, different sections of Indian society is given below., Section, , Number of girls per thousand boys, , Scheduled Caste (SC), , 940, , Scheduled Tribe (ST), Non SC/ST, Backward districts, Non-backward districts, Rural, Urban, , 970, 920, 950, 920, 930, 910

Page 177 :
175, IX Standard – Mathematics, , Chapter, 172 14 – Statistics, , 0, , Urban, , Rural, , Backward districts, , Non SC/ST, , Scheduled tribe, , Scheduled Caste, , 1000, 900, 800, 700, 600, 500, 400, 300, 200, 100, , Non - Backward districts, , Y, , Number of girls per thousand boys, , Ans., , (i) Represent the information above by a bar graph., (ii) In the classroom discuss what conclusions can be arrived at from the graph., , X, , Section, , ii. a. The number of girls to the nearest ten per thousand boys is maximum in scheduled tribe, section and minimum in urban section of the society., b. The number of girls ten per thousand boy is the same for non sc/st and non-back ward, districts., , Ans., , Given below are the seats won by different political parties in the polling outcome of a, state assembly elections:, Political, A B, C, D, E, F, Party, Seats, 75 55 37 29 10 37, Won, (i) Draw a bar graph to represent the polling results., (ii) Which political party won the maximum number of seats?, Y, , Seats won, , 3., , 80, 70, 60, 50, 40, 30, 20, 10, 0, , A, , B, , C, , Political Party, , D, , ii. Political party A won the maximum number of seats., , E, , F, , X

Page 178 :
176 14 – Statistics, Chapter, 4., , IX Standard – Mathematics, , 173, , The length of 40 leaves of a plant are measured correct to one millimetre, and the obtained, data is represented in the following table:, Length (in mm), , Number of leaves, , 118-126, , 3, , 127-135, 136-144, 145-153, 154-162, 163-171, , 5, 9, 12, 5, 4, , 172-180, 2, (i) Draw a histogram to represent the given data. [Hint: First make the class intervals, continuous], (ii) Is there any other suitable graphical representation for the same data?, (iii) Is it correct to conclude that the maximum number of leaves are 153 mm long? Why?, Ans. Modified continuous distribution, , Length in (mm), , 189.5, , 180.5, , 120.5, , 171.5, , 162.5, , Number of leaves, 3, 5, 9, 12, 5, 4, 2, , 153.5, , 144.5, , 135.5, , 126.5, , 13, 12, 11, 10, 9, 8, 7, 6, 5, 4, 3, 2, 1, 0, , 108.5, 117.5, , Length (in mm), 117.5 - 126.5, 126.5 - 135.5, 135.5 - 144.5, 144.5 - 153.5, 153.5 - 162.5, 162.5 - 171.5, 171.5 - 180.5, , ii. Frequency polygon, iii. No maximum number of leaves have their length b/w 145 to 153.

Page 179 :
177, IX Standard – Mathematics, , Chapter 14 – Statistics, , 174, , 5., , Life time (in hours), , Number of lamps, , 300-400, , 14, , 400-500, 500-600, 600-700, , 56, 60, 86, , 700-800, 800-900, , 74, 62, , 900-1000, 48, (i) Represent the given information with the help of a histogram., (ii) How many lamps have a life time of more than 700 hours?, Y, 90, 80, 70, 60, 50, 40, 30, 20, 10, , Number of lamps, , Ans., , The following table gives the life times of 400 neon lamps:, , 0, , 300 400 500 600 700 800 900 1000, Length (in mm), , X, , ii. Lamps having life time more than 700 hours is 74 + 62 + 48 = 184., 6., , The following table gives the distribution of students of two sections according to the, marks obtained by them:, Section A, , Section B, , Marks, , Frequency, , Marks, , Frequency, , 0-10, , 3, , 0-10, , 5, , 10-20, 20-30, 30-40, , 9, 17, 12, , 10-20, 20-30, 30-40, , 19, 15, 10, , 40-50, 9, 40-50, 1, Represent the marks of the students of both the sections on the same graph by two, frequency polygons.

Page 180 :
178 14 – Statistics, Chapter, , IX Standard – Mathematics, 175, , Ans. Modified table, Marks, 0-10, 10-20, 20-30, 30-40, 40-50, , Section A, Mid point, 5, 15, 25, 35, 45, , Frequency, 3, 9, 17, 12, 9, , Marks, 0-10, 10-20, 20-30, 30-40, 40-50, , Section B, Mid point, 5, 15, 25, 35, 45, , Frequency, 5, 19, 15, 10, 1, , 20, 18, , Frequency, , 16, 14, , Section A, , 12, 10, 8, 6, , Section B, , 4, 2, 0, , 7., , Ans., , 5 10 15 20 25 30 35 40 45 50, Marks, , The runs scored by two teams A and B on the first 60 balls in a cricket match are given, below:, Number of balls, , Team A, , Team B, , 1-6, , 2, , 5, , 7-12, 1, 6, 13-18, 8, 2, 19-24, 9, 10, 25-30, 4, 5, 31-36, 5, 6, 37-42, 6, 3, 43-48, 10, 4, 49-54, 6, 8, 55-60, 2, 10, Represent the data of both the teams on the same graph by frequency polygons. [Hint:, First make the class intervals continuous.]

Page 181 :
179, IX Standard – Mathematics, , Chapter, 176 14 – Statistics, No. of balls, 0.5-6.5, 6.5-12.5, 12.5-18.5, 18.5-24.5, 24.5-30.5, 30.5-36.5, 36.5-42.5, 42.5-48.5, 48.5-54.5, 54.5-60.5, , Class mark, 3.5, 9.5, 15.5, 21.5, 27.5, 33.5, 39.5, 45.5, 51.5, 57.5, , Team A, 2, 1, 8, 9, 4, 5, 6, 10, 6, 2, , Team B, 5, 6, 2, 10, 5, 6, 3, 4, 8, 10, , 10, 9, 8, 7, , Team B, , 6, 5, 4, 3, 2, , Team A, , 1, 0, –3.5, , 8., , 3.5, , 9.5 15.5 21.5 27.5 33.5 39.5 45.5 51.5 57.5 63.5, , A random survey of the number of children of various age groups playing in a park was, found as follows:, Age (in years), , Number of children, , 1-2, 2-3, 3-5, 5-7, 7-10, 10-15, , 5, 3, 6, 12, 9, 10, , 15-17, Draw a histogram to represent the data above., Ans. Length of rectangle, Frequency, =, × Common factor, Width of class, , 4

Page 182 :
Chapter, 180 14 – Statistics, Age, 1-2, 2-3, 3-5, 5-7, 7-10, 10-15, 15-17, , IX Standard – Mathematics, 177, , No. of children, 5, 3, 6, 12, 9, 10, 4, , Width of the class, 1, 1, 2, 2, 3, 5, 2, , Length of the rectangle, 5, 3, 3, 6, 3, 2, 2, , Length of Rectangle, , Y, 6, 5, 4, 3, 2, 1, 0, , 1, , 2, , 3, , 4, , 5, , 6, , 7, , 8, , 9, , 10 11 12 13 14 15 16 17, , X, , Age (in year), , 9., , 100 surnames were randomly picked up from a local telephone directory and a frequency, distribution of the number of letters in the English alphabet in the surnames was found, as follows:, Number of letters, , Number of surnames, , 1-4, 4-6, 6-8, 8 -12, , 6, 30, 44, 16, , 12 -20, 4, (i) Draw a histogram to depict the given information., (ii) Write the class interval in which the maximum number of surnames lie., Ans. Length of rectangle, Frequency, =, × Common factor, Width of class, Common factor = 2, No. of letters, , No. of surnames frequency, , Width of class, , Length of rectangle, , 1-4, 4-6, 6-8, 8-12, 12-20, , 6, 30, 44, 16, 4, , 3, 2, 2, 4, 8, , 4, 30, 44, 8, 1

Page 183 :
181, IX Standard – Mathematics, , Chapter 14 – Statistics, , 178, , Y, 48, 44, 40, 36, 32, 28, 24, 20, 16, 12, 8, 4, , Sum of all the observation, Total no.of observation, 2 + 3 + 4 + 5 + 0 +1+ 3 + 4 + 3, =, 10, 28, = = 2.8, 10, ii.Median, Arrange the given scores in ascending, order 0,1, 2,3,3,3, 4, 4,5, i.Mean =, , No.of scores is = 10, which is even, \ Median is average of middle two scores, , 5th score + 6 th score 3 + 3 6, =, = = 3, 2, 2, 2, Median = 3, X, 0, 1 2 3 4 5 6 7, 8 9 10 11iii.Arrange, 12 13 14 the, 15given, 16 17, 18 19, scores, in 20, ascending order, Exercise 14.4, 0,1, 2,3,3,3,3, 4, 4,5, 3occurs most frequently (4 times), 1., The following number of goals were, \ Mode =, 3, scored by a team in a series of 10 matches:, 2, 3, 4, 5, 0, 1, 3, 3, 4, 3, 2., In a mathematics test given to 15 students,, Find the mean, median and mode of, the following marks (out of 100) are, these scores., recorded:, Ans., 41, 39, 48, 52, 46, 62, 54, 40, 96, 52, 98,, Sum of all the observation, 40, 42, 52, 60, i.Mean =, Total no.of observation, Find the mean, median and mode of this, 2 + 3 + 4 + 5 + 0 +1+ 3 + 4 + 3, data., =, Ans., 10, Sum of all the observation, 28, i.Mean =, = = 2.8, Total no.of observation, 10, 41 + 39 + 48 + 52 + 46 + 62 + 54, ii.Median, Arrange the given scores in ascending, order 0,1, 2,3,3,3, 4, 4,5, No.of scores is = 10, which is even, \ Median is average of middle two scores, 5th score + 6 th score 3 + 3 6, =, = = 3, 2, 2, 2, Median = 3, iii.Arrange the given scores in, ascending order, 0,1, 2,3,3,3,3, 4, 4,5, 3occurs most frequently (4 times), \ Mode =, 3, =, , =, , +40 + 96 + 52 + 98 + 40 + 42, +52 + 60, =, 15, 822, = = 54.8, 15, ii.Median, Arrange the given scores in ascending, order 39, 40, 40, 41, 42, 46, 48,52,52,, 52,54, 60, 62,96,98, No.of scores is n =15, which is odd, 15 + 1, \ Middle of score is median =, 2, th, = 8 score

Page 184 :
= 54.8, 15, ii.Median, Arrange the given scores in ascending, 182order1439,– 40,, 40, 41, 42, 46, 48,52,52,, Chapter, Statistics, 52,54, 60, 62,96,98, No.of scores is n =15, which is odd, =, , IX Standard – Mathematics, 179, , Salary (in Rs), 15 + 1, \ Middle of score is median = 3000, 2, 4000, = 8th score, \ Median is average of middle two scores, \ Median is 52, iii.Arrange the given scores in, ascending order, 39, 40, 40, 41, 42, 46, 48,52,52,, 52,54, 60, 62,96,98, \ 52 repeted more times(3 times), \ Mode =, 52, , The following observations have been, arranged in ascending order. If the, median of the data is 63, find the value, of x., 29, 32, 48, 50, x, x+2, 72, 78, 84, 95, Ans. Number of scores n = 10 which is even, 5th + 6 th, Median =, 2, x+x+2, 63 =, 2, 63 × 2 = 2x + 2, 2x + 2 =, 126, 2x = 124, 124, =, x = 62, 2, Hence, the value of x is 62, Find the mode of 14,25,14,28,18,17,18,1, 4,23,22,14,18., Ans. Arrange the score in ascending order, we, have 14,14,14,14,17,18,18,18,22,23,25,28, \ 14 repeated more time (4 times), \Mode = 14, 5., , Find the mean salary of 60 workers of a, factory from the following table:, , 16, 12, , 5000, , 10, , 6000, , 8, , 7000, , 6, , 8000, , 4, , 9000, , 3, , 10000, , 1, , Total, , 60, , Ans., Salary (in Rs), No. of workers, x, , 3., , 4., , Number of workers, , 3000, , 16, , 48000, , 4000, 5000, 6000, 7000, 8000, 9000, , 12, 10, 8, 6, 4, 3, , 48000, 50000, 48000, 42000, 32000, 27000, , 10000, , 1, , 10000, , Total, , Sf=n=60, , Sfx=30500, , Mean, =, , 6., , Fx, , ∑ fx 305000 30500, =, =, n, 60, 6, = 5083.33, , Give one example of a situation in which, (i) the mean is an appropriate measure, of central tendency., (ii) the mean is not an appropriate, measure of central tendency but the, median is an appropriate measure of, central tendency., Ans. i. Mean runs scored by a batsman in series, ii. Average beauty.

Page 185 :
183, IX Standard – Mathematics, , Chapter, 180 14 – Statistics, Additional Problems, , I., , Multiple Choice Question s, , 1., , The range of the following frequency, distribution is 2.7,2.8,2.1,2.4,3.2,2.1,3.1,, 2.8,3.2, a) 1.1, b) 0.55 c) 2.4 d) 3.2, , 2., , The lower limit of the class interval 21 30 is, a) 30, b) 21, c) 21.5 d) 20.5, , 3., , The upper of the class interval 21 - 30 is, a) 30, b) 21, c) 30.5 d) 29.5, , 4., , The width of the class interval 29.5 34.5, a) 10, b) 2.5 c) 5, d) 4, , 5., , Mean of first 10 natural number is, a) 55, b) 25, c) 5.6 d) 5.5, , 6., , The mean two numbers is 6 and mean, of three numbers is 7 the value of third, number is, a) 2, b) 9, c) 5, d) 4, , 7., , Median of the following numbers, 4,4,5,7,6,7,7,12,3 is, a) 4, b) 5, c) 7, d) 6, , 8., , 15,14,19,20,, , Mode of the following data, 14,15,18,14,19,15,17,15 is, a) 14, b) 15, c) 16, Ans. 1) a, 2) b, 3) a, 5) d, 6) b, 7) d, , Ans., Class, Interval, 25 - 35, 35 - 45, 45 - 55, 55 - 65, 65 - 75, 75 - 85, 85 - 95, 95 - 105, 2., , Ans., , 1111 11, 1111 1111, 1111 111, 1111 1111, 111, , 7, 9, 8, 9, 3, 0, 2, 3, 41, , 11, 111, , Find the mean, distribution, x, f, , 4, 4, , 6, 8, , of, , the, , following, , 8 10 12, 14 11 3, fx, 16, 48, 112, 110, 36, ∑ fx = 322, , ∑ fx, Fx, n, 322, = = 8.05, 40, Mean = 8.05, , d) 17, 4) c, 8) b, , The electricity bills of 41 houses in a, locality are given below. Construct a, frequency distribution table with a class, size of 10,30,35,37,28,32,34,40,50,47,46,, 55,52,44,43,44,45,61,60,59,25,26,27,48,4, 9,50,41,42,43,57,58,56,55,60,70,72,69,88, ,89,101,103,99., , Frequency, , x, f, 4, 4, 6, 8, 8, 14, 10, 11, 12, 3, ∑ f = n = 40, Mean =, , Answer the following questions, , 1., , Tally Mark, , 3., , Find the median and mode for the data, 17,2,7,27,25,5,14,18,10,24,48,10,8,7,10,28, Ans. Arrange the given data in ascending order., 2,5,7,7,8,10,10,10,14,17,18,24,25,27,28,48, 8th score + 9 th score 10 + 14, Median =, =, 2, 2, 24, = = 12, 2, Median =12, \Mode = 10 (occurs 3 times)

Page 186 :
184 14 – Statistics, Chapter, 4., , Ans., , IX Standard – Mathematics, 181, , Draw a histogram of the following, distribution., Heights (in m) No. of students (F), 150 - 153, 7, 153 - 156, 8, 156 - 159, 14, 159 - 162, 10, 162 - 165, 6, 165 - 168, 5, y, 16, 14, 12, 10, 8, 6, 4, 2, , 0, , 5., , Ans., , x, , 150 153 156 159 162 165 168, , Find the missing frequency ‘k’ from the, following data given mean is 16., x, f, , 5, 2, , 10, 8, , 15, k, , 20, 10, , x, f, fx, 5, 2, 10, 10, 8, 80, 15, k, 15k, 20, 10 200, 25, 5, 125, n =k + 25 ∑ fx =415 + 15k, ∑ fx, Mean =, n, 415 + 15k, 16 =, k + 25, 16 ( k + 25 ) = 415 + 15k, 16k + 400 = 415 + 15k, 16k −15k = 415 − 400, k =15, , 25, 5, , 6., , The mean of first 8 observations is 18, and last 8 observations is 20. If the mean, of all 15 observations is 19. Find the 8th, observation., Ans. Mean of 8 observations = 18, Sum of observations = 18 x 8 = 144, Sum of last 8 observations = 8 x 20 = 160, Sum of all 15 observations = 15 x 19 = 285, \8th observation = (144 + 160) - 285, = 304 - 285 = 19

Page 187 :
182, , 185, , Chapter, 15, CHAPTER --15, , Probability, Probability, Key Points :, , ●, ●, ●, ●, ●, , Trial : It is an action which results in one or more out comes., Event : An experiment is the collection of some of its out comes., Sample space : All possible out comes of a random experiment., Random experiment : an experiment whose exact outcomes cannot be predicted., Empirical probability : The ratio of number of trials in which the event occured to the total, number of trials., Classical probability : The ratio of number of outcomes favorable to the number of all possible, out comes of the experiment., Number of out comes favourable, Probability =, Total number of all possible outcomes, , ●, ●, ●, , Probability of a certain event or sure event is one., Probability of a impossible event is zero., Probability of an event is never negative., , Exercise 15.1, , Number of girls in a family 2, , 1., , In a cricket match, a batswoman hits, a boundary 6 times out of 30 balls she, plays. Find the probability that she did, not hit a boundary., Ans. Let E be event of hitting the boundary by, bats women is 6 times., Let the s be an number of balls faced by, bats women is 30, \n(s) = 30, Let E1 be the event of not hitting the, boundary by bats women is = 30 – 6 = 24, \ n ( E1 ) =, 24, Probability, =, 2., , n ( E1 ) 24, 4, =, ( or ), n ( s ) 30, 5, , 1500 families with 2 children were, selected randomly, and the following, data were recorded:, , 1, , 0, , Number of families, 475 814 211, Compute the probability of a family,, chosen at random, having, (i) 2 girls (ii) 1 girl, (iii) No girl, Also check whether the sum of these, probabilities is 1., Ans. Let S be an total families selected in, random experiment, \S = 475 + 814 + 211, \n(s) = 1500, i. Let A be an event of an choosen family, has 2 girls, \n(A) = 475, Probability of a family, chosen at random,, having two girls, n ( A ) 475 19, Probability, = = =, n ( s ) 1500 60

Page 188 :
186 15 – Probability, Chapter, , IX Standard – Mathematics, , 183, , n(s) = 200, Let A be an event of appear 2 head is, n(A) = 72, n (A), Probability of getting 2 heads =, n (s ), , ii. Let B an event of an chosen family at, random has 1 girl, \ n ( B) =, 814, Probability, =, , n ( B ) 814 407, = =, n ( s ) 1500 750, , iii. Let c be an event of an chosen family at, random having no girl, \ n (c) =, 211, n ( c ) 211, = =, Probability, n ( s ) 1500, Sum of all probabilities, 19 407 211, = +, +, 60 750 1500, 475 814, 211, =, +, +, 1500 1500 1500, 1500, = = 1, 1500, 3., , Refer to Example 5, Section 14.4,, Chapter 14. Find the probability that a, student of the class was born in August., Ans. Total number of students born in the year, =3+4+2+5+1+2+6+3+4+4+, 4 = 40, \n(s) = 40, Let the A be event number of students born, in August, \n(A) = 6, Probability of a student born in August, =, 4., , n (A) 6, 3, = =, n ( s ) 40 20, , Three coins are tossed simultaneously, 200 times with the following frequencies, of different outcomes:, Outcome 3 heads 2 heads 1 head No head, , Frequency 23, 72, 77, 28, If the three coins are simultaneously, tossed again, compute the probability of, 2 heads coming up., Ans. Total number of times 3 coins tossed, simultaneously = 23 + 72 + 71 + 28 = 200, , =, 5., , 72, 9, =, 200 25, , An organisation selected 2400 families, at random and surveyed them to, determine a relationship between, income level and the number of vehicles, in a family. The information gathered is, listed in the table below:, Monthly income, (in Rs), , Vehicles per family, 0, , 1, , 2, , Less than 7000, , 10, , 160, , 25, , Above 2, 0, , 7000 – 10000, , 0, , 305, , 27, , 2, , 10000–13000, , 1, , 535, , 29, , 1, , 13000–16000, , 2, , 469, , 59, , 25, , 16000 or more, , 1, , 579, , 82, , 88, , Suppose a family is chosen. Find the, probability that the family chosen is, (i) earning Rs 10000 - 13000 per month, and owning exactly 2 vehicles., (ii) earning Rs 16000 or more per month, and owning exactly 1 vehicle., (iii) earning less than Rs 7000 per month, and does not own any vehicle., (iv) earning Rs 13000 - 16000 per month, and owning more than 2 vehicles., (v) owning not more than 1 vehicle., Ans. Total number of families selected is 2400, \ n (s ) =, 2400, families, i.Let ' A ' be event number of, families, Rs10000 − 13000 per month having, exactly 2 vehicles is 29 n ( A ) = 29, Probability, =, , n (A), 29, =, n ( s ) 2400, , ii. Let ‘B’ be event number of families, earning Rs 16000 or more per month

Page 189 :
\n(s) = 90, lives:, i. Let ‘A’ be event student obtained less, (i) less, than 20% in mathematics test = 7, work?, n(A) = 7IX Standard – Mathematics, (if) mor, 184, Chapter 15 – Probability, Probability student obtained. Less 187, than, place of, 20% in mathematics test, (iii) wit, owing exactly one vehicle is 579., n ( B ) 23, n (A) 7, = =, work?, n(B) = 579, = n (=, S) 60, Ans., nu, n ( B ) 579184, n, s, 90, 193, (, ), IX StandardTotal, – Math, IX Standard – Mathematics, 184, Probability, = = =, n(S), =, 4, n ( s ) 2400 800, 7. Toii.know, thebe, opinion, the students, about, Let ‘B’, event of, student, obtained, marks, i., Let, A, owing, exactly, one, vehicle, is, 579., owing exactly one vehicle is 579., n (=, Bof)23200, 23, the60nsubject, survey, Standard, –23., Mathematics, ( Babove, ) IX, or, is 15 + 8 =a=, n(B), 23statistics,, 184, iii. n(B), Let =‘C’, families, whose d, =, n(B), = 579, = =, 579be event number of, students, Then (data, is60, S, Probability, student obtained, marks, ) 60, n S was, 60ofconducted., earning less thann7000, Rs579, per month, 579( ) 193, ( B )vehicle, 193 does n ( B ) recorded, owing, exactly, one, is, 579., in, the, following, table., = = or, =, =vehicle, =is 10, = Probability, nabove, ( B ) in, 23mathematics, not Probability, have own, IX, Standard – test, Mathematics, 184, n 7., s ) To, 2400, (=, n ( s ) 2400 800, =800, n(B) = 579, 7. students, Tostudents, know, the opinion of the stude, know, the opinionNumber, of the, about, of, \n(c) = 10, nOpinion, S, 60, (subject, ), n, B, the, subject, (, ), 579, 193, the, statistics,, a, survey, of, 200 statistics, a surve, iii., Let, ‘C’, be, event, number, of, families, IX, Standard, –, Mathematics, iii., Letexactly, ‘C’ nbe, 184 owing, vehicle, is 579., Probability, =, =, =, ( cone, )event, 135, 10number, 1 of families, n ( Blike, ) month, 23 conducted., students, was, students, was, The, data, is conducted. The, n, s, 2400, 800, earning, less, than, 7000, Rs, per, does, (, ), Probability, =, =, =, earning, less, than, 7000, Rs, per, month, does, = the opinion of the students about, n(B) = 579, 7.=To know, recorded, in, n, s, 2400, 240, n, S, 60, recorded, in, the, following, table., (, ), (, ), 65 of 200the following table., not, have own vehicle the, is 10Dislike, not, have, own, 10, subject statistics, a survey, n event, B ) isnumber, owing, exactly, one, is 579., (vehicle, 579, 193, iii., Let, ‘C’, bevehicle, of families, n, B, (, ), 23, Probability, =, =, =, Opinion, Number of s, \n(c) = 10, Opinion, Number, ofastudents, =less, 10, Find, the was, probability, thatThe, student, students, conducted., data, is, =, n(B), = 579, iv. \n(c), Let, ‘D’, be than, event, number, families, earning, Rs perof800, month, does =, n ( s7000, 2400, ), 7., To, know, the, opinion, of, the, students, about, n, c, n, S, 60, ( ) chosen, like, 135, 10( ) at, 1random, n ( c ) is10, like, 135, 1 month, recorded, in the following table., not, have, own, 10 193, earning, Rs, 13000, 16000, per, n (vehicle, B=, Probability, = = the, =, ) – 579, Probability, =, =, subject statistics, a survey of 200, iii., Let, ‘C’ be, event, number, of families, Probability, =, =, =, n, s, 2400, 240, (i), likes, statistics,, (ii), does, not, like, it., (, ), n, s, 2400, 240, Opinion, Number, of, students, Dislike, 65, (, ), \n(c), =, 10, Dislike, 65, having, more, vehicle, is800, 25., \n(D), students was conducted. The data is, nthan, 2400, earning, lessthan, Rs per, month, does 7., (ns )(2c7000, To, know, the opinion, of thein, students, about, Ans., Total, number, of, students, survey, is, 200., Find, the, probability, that, a, Find, the, probability, that, a, student, ), like, 135, 10, 1, in families, the following table., = 25, ‘D’ be event recorded, number of, iv., Let, ‘D’, event isnumber, families, not, have, ownbevehicle, 10 iv.ofLet, Probability, =, =, =, the, subject, statistics,, a, survey, of, 200, chosen, at, random, n(S), =, 200, chosen, at, random, iii. \n(c), Let, ‘C’, be, event, number, of, families, 2400, Rs 13000 – 16000, per month Number 65, earning= 10, Rs n13000, 16000earning, per month, Dislike, Opinion, of students, ( nD()s ) –25, 1240, was, conducted., The, data, (i), likes, statistics,, (ii) does no, (i), statistics,, (ii) does, not, like, it.is, Probability, =, =, =, i.vehicle, Letlikes, ‘A’, be, event, students., Like, earning, less, than, 7000, Rs10per month, does, having, more than 2 students, is, 25.probability, \n(D), having, more, than, 2, vehicle, is, 25., \n(D), Find, the, that, a statistics, student, n, c, (, ), like, 135, 1, iv., Let, ‘D’, be, event, number, of, families, n, s, 2400, 96, (, ), Ans., Total, number, of, students, in surve, Ans., Total, number, of, students, in, survey, is, 200., recorded, in, the, following, table., Probability, =vehicle, =is 10, = = 25, ischosen, 135 n(A), = 135, not=, have, 25 own, at random, earning, Rs 13000, 16000 240, per month, n ( s ) –2400, Dislike, 65, n(S), =, 200, n(S), =, 200, n ( D ) (i)25, Opinion, Number, 1, n ( D2)number, nnot, A )like it., likes, statistics,, (ii) doesof, \n(c), 10more, (astudents, 25 of 125., v. having, Let =‘E’, be event, families, than, vehicle, \n(D), = = Probability, =, i. Let, ‘A’ be event students. Like, Find, thebe, that, student, Probability, =, =, = isProbability, i., Let number, ‘A’, event, students., Like, statistics, ofprobability, likestatistics, =survey, iv., Let, ‘D’, be, event, number, of, families, Ans., Total, of, students, in, 200., n, s, 2400, 96, owning, not, more, than, 1, is, (10+0+1+2+1), n, c, (, ), n, s, 2400, 96, ( )( ) 10, like, 135, 1, = 25, S) isn(A), (, isn 135, = 135, chosen, at random, is, 135, n(A), =, 135, Probability, =, =, =, earning, Rs, 13000, –, 16000, per, month, n(S), =, 200, +(160+305+535+469+579), =, 14, +, 2048, =, n, D, (, ), 25, 1, (i), likes, statistics,, (ii), does, not, like, it., n(, n, s, 2400, 240, v., Let, ‘E’, be, event, number, of, families, n, A, (, ), ( statistics, ), 65, v., Let ‘E’, event, number, 135, 27, having, morebethan, 2 vehicle, 25.families, \n(D), Probability, =, = is of, i.Probability, LetDislike, ‘A’ be, students.=Like, Probability, of like statistics =, ofevent, like, statistics, 2062, n(D)=, = 2062, =, =, Ans., Total, number, of, students, in, survey, is, 200., n, s, 2400, 96, owning, not, more, than, 1, is, (10+0+1+2+1), (, ), owning, not, more, than, 1, is, (10+0+1+2+1), n(, 25 ‘D’ be event number of families, Find, that na( Sstudent, ), is 135the, n(A)probability, = 13540, 200, iv. =Let, n ( nE()D ) 206225 =1031, n(S) ==200, +(160+305+535+469+579), 14, + 2048 =, +(160+305+535+469+579), 14, +families, 2048 =, 1, chosen, at, random, n, A, (, ), v., Let, ‘E’, be, event, number, of, 135, 27, Probability, =, =, =, 135, 27, earning, Rs, 13000, – 16000, per month, Let=, ‘B’, belikeevent, students, dislike=, Probability, =, = 2062, Let, ‘A’, beof, event, students., n(D) = 2062 ii.i.Probability, statistics, =Like statistics, =, 2062, n(D), 2062, =, nmore, 2400, 1200, ( sn=, )2( sthan, (i)islikes, statistics,, (ii) does, not, it.200 40, owning, not=, 1 isis(10+0+1+2+1), 2400, 96 \n(D), )vehicle, n ( Slike, ), 200, 40, having, more, than, 25., 135, n(A), =, 135, statistics, is, 65, n(B), =, 65, n, E, (, ), 2062, 1031, n, E, ( ) 2062 = Probability, 1031, +(160+305+535+469+579), 14, + 2048, = Ans., Total, number, of, students, in, survey, is, 200., =, =, =, Probability, =, =, =, ii., Let, = 25, n (nA, Let 1200, ‘B’135, be event, students, 27, v. Let ‘E’ be nevent, number, of families n ( s ) ii., ()Bdislike, ) ‘B’ be event student, 2400, 2400 14., 1200, ( s )Chapter, 2062, = 2062, 6. Refer, ton(D), Table, 14.7,, =, Probability, of, like statistics =statistics, n(S), ==, 200isof, Probability, dislikestatistics, =n ( S) is 65 n(B) = 65, statistics, 65, n(B)40, = 65, owning not nmore, than251 is (10+0+1+2+1), D, (, ), 200, 1, n (E) =, s), (i), Find, the probability, that 14, a1031, student, 2062, Probability, =, =, Let ‘A’ be event students. Likennstatistics, +(160+305+535+469+579), + 2048, = 14.7,i.Chapter, (( Bdislike, ) of dislike statistics =, Probability, =, =, 6. =96, Refer, to Table, 6. obtained, Refer, to, Table, 14.7,, Chapter, 14., ii., Let 14., ‘B’135, be, event, students, n (ns=, 2400, 27, ), Probability, Probability, of, dislike, statistics, =, less, than, 20%, in, the, s, 2400, 1200, (), is 135 that, n(A), 135 13, 2062, n(D)the, = 2062, =isa=65, =, (i) aFind, the probability, student, n, s, (i) Find, probability that, student, (, ), statistics, 65, n(B), =, 65, = =, 200 40, mathematics, n ( E than, n ( A )B ), ) number, 206220%, 1031, v., Let ‘E’ betest., event, of, families, obtained, in, the, less, in theless than 20% 200, 40, 65 13, 65, 13 statistics, Probability, =, =, =, 6. (ii)obtained, Refer, to, Table, 14.7, Chapter, 14., Probability, of, likestatistics, = = n (=, Find, the, probability, that, a, student, ii., Let, ‘B’, be, event, students, dislike=, Probability, dislike, = of, =, mathematics, test., owning, not moretest., is (10+0+1+2+1), nthan, s ) 1 2400, 1200, mathematics, (, n, S, (, ), n, s, (i), Find, the, probability, that, a, student, 200, 40, ) the, 200, statistics, isa65, n(B)40, = 6514.2. What( is, obtained, marks, 60 or above., 8. Refer, to Q.2,, Exercise, (ii)+aFind, the, that, student, (ii), Find, theless, probability, that, student, +(160+305+535+469+579), =20%, 14, 2048, = probability, obtained, than, in, the, 135, n ( B), 65 27, 13 that, Ans., Total, number, of students, is, 90 obtained, marks8.60 empirical, orRefer, above., 6. 2062, Refer, to=Table, 14.7,, Chapter, 14., probability, obtained, marks, 60 or, above., 8.14.2.an, Refer, to, n(D), 2062, to Q.2,, Exercise, What, is Q.2,, the Exercise 14.2. Wh, =, =, =, =, Probability, of, dislike, statistics, = engineer, mathematics, test., \n(s), =, 90, 200, 40, Ans., Total, number, of, students, is, 90, nengineer, s ) probability that an, 200, 40, (i), Find, the, probability, that, a, student, (, Ans., Total, number, of, students, is, 90, empirical, lives:, empirical, probability, that, an, Marks, Number, of, students, n, E, ) than, (ii) Find the (probability, 2062 that, 1031a student, \n(s)in=less, 90, obtained, less, 20%, the, \n(s), =be, 90, =, =60, =, i.Probability, Let, ‘A’, event, student, obtained, lives:, (i)lives:, less, 7Exercise, km, her, place, of, 65, 13 from, Let tothan, ‘B’, be, event, students, dislike, obtained, marks, or, above., 0 – 20, 7 1200, 8. ii., Refer, Q.2,, 14.2., What, is the, n, s, 2400, (, ), =, =, i.7 Let ‘A’less, be event, student, obtained, less, mathematics, test., i., Let, ‘A’, be, event, student, obtained, (i), less, than, 7, km, her, place, of, work?, less, than, than, 20%, in, mathematics, test, =, (i), less, than, 7, km, from, her, place, of 7 km from her, work?, 20 – 30, Ans. Total, number of students10is 90, statistics, is 65, n(B) 40, = 65 that (i), 200, empirical, probability, an, engineer, than, in mathematics, test, = 7than or equal towork?, (ii), Find, the, probability, that, a 20%, student, than, 20%, in, mathematics, test, =, 7, (ii), more, 7, km, from, her, work?, n(A), =, 7, 30, –, 40, 10, \n(s) = 90, (if), more than or equal to 7 km nfrom, lives:, ( Bis) her, n(A) = 7, 6. Refer, 14.7,60Chapter, obtained, or above., n(A), =Table, 7 marks, (if), more, than or equal to 7 km, Refer, to, Q.2,, Exercise, 14.2., What, the, –to50, 20 14., (if), more, than, or, equal, to, 7, km, from, her, place, of, work?, Probability, of, dislikestatistics, =, Probability, student, Less than, i.40Let, ‘A’, be eventobtained., student, obtained, less 8. place, of work?, (i) less, than, 7 than, km from her place of, Less, Ans., Total, number, of students, is 90Probability, Probability, student, thanstudent obtained., nengineer, (i), Find, theinprobability, that, a Less, 50 – 60, 20, ( sofof, ) work?, place, empirical, probability, that, an, place, of work?, (iii)within, within, 1/2m, from, herher, place, work?, than, mathematics, test =, 7student, 20%, in 20%, mathematics, testobtained., work?, (iii), 1/2, km, from, place, of1/2 km from her, 20%, in, mathematics, test, 60, –, 70, 15, \n(s), =mathematics, 90, 20%, in, test, (iii), within, lives:, obtained, less, than, 20%, in, the, (iii), within, 1/2, km, from, her, place, of, n(A), =, 7, The, distance, (in, km), of, 40, engineers, 65, 13, (if), more, than, or, equal, to, 7, km, from, her, n70, A, (, ), 7, work?, above, 8, i., Let, ‘A’, be, event, student, obtained, less, n, A, (, ), 7, n ( A ) test., = than, =7 km from her, work?, 7student obtained. Less than, (i), less, place of, work?, mathematics, =, =, Probability, =, place, oftheir, work?, fromnumber, residence, to their isplace, of, =than, 200of, 40, engineers, mathematics, test = 7n=, nFind, 90in90, Total, ( sn=, )(20%, Ans., Total number, of female enginee, work?, Ans.Total, Total, number, of female, female, engineers, is 40., 40., ( s ) 90 Ans., s )the, (ii)20%, probability, that, a student, in, mathematics, test90, (iii), within, 1/2, km, from, her, place, of, work, were, found, as, follows, 5,3,10,2,25,, n(A) = 7, n(S), =, n(S)from, = 40 her, (if), more, n(S), =40, 40 than or equal to 7 km, n‘B’, obtained, marks, 60student, orstudent, above., ( A‘B’, )be be, 7 event, work?, 8. student, Refer, to, Q.2,, Exercise, 14.2., is, ii., Let, event, obtained, marks, ii. Let, ‘B’, be event, obtained, marks, 11,13,7,12,31,19,10,12,17,18,11,32,17,1, ii., Let, obtained, marks, Probability, student, obtained., Less, than, =, =, i.What, Let, A the, be an event female, i.place, Let, A, be, an, event, female, engineers, ofAwork?, i., Let, be, an, event, female, engineers, Total, number, of female, engineers, is 40., Ans. 60, Total, of, 90n(B), n (in, sabove, 60= or, above is 15Ans., + 8empirical, =, 23., n(B), =, 23, ) mathematics, probability, that, an, engineer, or number, above, is90, 15, + 8+ =8test, 23., n(B), 2323, 60, or, is students, 15, = is23., =, 6,2,7,9,7,8,3,5,12,15,18,3,12,14,2,9,6,15,, 20%, whose, distance, (iii), within, 1/2, km, from, her, place, of, whose, distance, less, than, 7km, is, a, n(A), whose, distance, less, than, 7km, is, a, n(A), =, 9 less than 7km is a, n(S), = 40 marks 60, \n(s), Probability, obtained, Probability, student, obtained, marks, lives:, Probability, student, obtained, marks, 6060of student, n=( A90, 15,7,6,12., ) ofbe7of, work?, ii., Let, ‘B’, event, student, obtained, marks, i. Let, A be an event female engineers, =, =, or above in mathematics, testnumber, i. Let, ‘A’inbe, student, obtained, or, in event, mathematics, test, less, than 7ofkm, fromengineers, her place, of, or, above, Ans.(i)Total, female, is 40., 60 above, or, 23., n(B) = 23less, n ( sabove, 90is 15 + 8 =test, ) mathematics, whose, distance, less than 7km is a n(A) = 9, than, 20% in mathematics, test = 7 marks 60, work?, n(S) = 40, Probability, of student obtained, ii. =, Let, event student obtained marks, n(A), 7 ‘B’inbemathematics, i. more, Let Athan, be an, event to, female, engineers, or above, test, (if), or equal, 7 km from, her, 60, or, above, is, 15 +obtained., 8 = 23. n(B), = 23than, whose, distance, less, than, 7km, is, a, n(A) = 9, Probability student, Less, place, of, work?, Probability of student obtained marks 60, 20% in mathematics test, (iii) within 1/2 km from her place of, or above in mathematics test, n (A) 7, work?, = =, Ans. Total number of female engineers is 40., n ( s ) 90

Page 190 :
Chapter, 15, Chapter, 15–––Probability, Probability, by 3., 185, Probability, of distanceChapter, less than 7km, Chapter, 15, Probability, 15 – Probability3, if the sum of its digits is divisible185, 185, Ans. Let the number of students in is 15. Three, n (A) 9, 3,, the, sum, isisdivisible, 3., digits, numbers, written, each, are by, 124,, 3,if, the, sumof, ofits, itsdigits, digitsby, divisible, by, 3., =Probability, = of, Probability, ofdistance, distanceless, lessthan, than7km, 7km, 3,, ififthan, the, sum, of, its, digits, divisible, by, 3., 3, if the185, sum, of its digits is d, Probability, of, distance, less, than, 7km, Probability, of distance, less, 7km, IX, Standard, –is789,, Mathematics, S) – Probability, 40, 188 n (15, Chapter, Ans., Let, the, number, of, students, in, isis999,, 15., Three, 136,, 135,, 246,, 369,, 562,, 444,, Ans., Let, the, number, of, students, in, 15., Three, Ans. Let the number of students, 15.number, Three of students in, Ans. in, Letisthe, nn((AA)) 99, digits, numbers, written, 256,, 569, 721,, 432, by, 153., digits123,, numbers, written, by each, each are, are 124,, 124,, ( A ) ‘B’9 be event female nengineers., (A) 9, =, =ii. n=, =, Let, digits, numbers, written, by, each, 124,, digitsare, numbers, =, =, = =, 3,, if, the, sum, of, its, digits, is, divisible, by, 3. written by e, n, S, 40, n, S, 40, (, ), (, ), 136,, 135,, 246,, 369,, 562,, 789,, 999,, 444,, Three, digit, numbers, divisible, by, 3, are, 135,, 136,, 135,, 246,, 369,, 562,, 789,, 999,, 444,, Probability, of distance, lessmore, thann7km, n ( S)distance, 40, S) their, 40, Whose, 7km (or), from, (, 136,, 135,, 246,, 369,, 562,, 789,, 999,, 444,, 136,, 135,, 246,, 369, 562, 78, Ans. Let, number, of students, in432, is 15., Three, Chapter 15 – Probability, 185, 256,, 123,, 569,, 721,, 432,, 153., 246,, 369,, 789,, 444,, and, 153., 256,the, 123,, 569,999,, 721,, 432,123,, 153., ii., Let, ‘B’, be, event, female, engineers., work, place, is, 31., n(B), =, 31, ii., Let, ‘B’, be, event, female, engineers., 256,, 123,, 569,, 721,, 432,, 153., (, ), 256,, 123,, 569,, 721,, 432, 153, n, A, 9, Let ‘B’ be event female, engineers., ii. Let, ‘B’ be event Three, female, engineers., digits, numbers, written, by each, numbers, by, are, 135,, =ii., =, n(A), =digit, 9&, n(s), =, 15divisible, Three, digit, numbers, divisible, by333are, are124,, 135,, Whose, distance, 7km, (or), more, from, their, Whose, distance, 7km, (or), more, from, their, Three, digit, numbers, divisible, by, are, 135,, n, B, Three, digit, numbers, divisible, (, ), n, S, 40, ( )distance, Whose, 7km, (or), more, their, Whose, from, their, 3,, ifmore, the, of, its, is789,, divisible, 3., (369,, 136,, 135,, 246,, 562,, 999,, 444,, 246,, 369,, 789,, 444,, 432, and, 153., 246,, 369,sum, 789,, 999,, 444,, 123,, 432, andby, 153., = from, Probability, of, 7km, (or), more, n999,, A )digits, 9 123,, 3246,, Probability, of31., distance, less, than, 7kmdistance 7km (or), work, place, is, n(B), ==, 31, work, place, is, 31., n(B), 31, 246,, 369,, 789,, 999,, 444,, 123,, 432, and, 153., 369,, 789,, 999,, 444,, 123,, Probability, =, =, =, n, S, work, place, is 31. n(B) = 31 work( place, ) is 31. Ans., n(B) n(A), =, 31the, Let, of15, students, is 15. Three, 256,, 123,, 569,, 432,, ==99number, &, n(s), n(A), &, n(s), (=, )15, ii. nLet, n721,, 15153., 5in, n(A), =9&, n(s), ==S15, B, n(A), =, 9, &, n(s), =, 15, (((B, ), A )‘B’ 9be event female nnnengineers., ), (, B), n (B, digits digit, numbers, 124,, ) nnn(((written, Three, numbers, by 3 are 135,, == from, Probability, of, (or), more, AA))) divisible, 99by 33each, 31, Probability, of7km, 7km, (or), more, =Whose, =, distance, 7km, (or), more, ( ), = nn((SS)) their, Probability, of, 7km, (or), more, A=, 9=, 3, = =, Probability, of 7km (or)Probability, more, = 40, Probability, =, =, =, n, S, (, ), 136,, 135,, 246,, 369,, 562,, 789,, 999,, 444,n A= 9= 3, 246,, 369,, 789,, 999,, 444,, 123,, 432, and, 153., 11., Eleven, bags, of, wheat, flour,, each, marked, Probability, =, =, =, =, n ( S), n ( S) nn(((SS))) 15, work place is, 4031. n(B) = 31, 15 555Probability, n, S, 15, n, 9 &569,, n(s)721,, =, 15432, 153., 256,, 123,, 5n(A), kg,=, actually, contained, the following ( S) 15 5, 31, 31, ii. Let, be event, event female, ( B ) 31, iii., Let ‘B’, ‘c’, femalen engineers., engineers, == 31be, (wheat, ) divisible, Three, numbers, by 3marked, are 135,, bags, of, flour,, each, = 40, weights, of=flour(inkg):, 11. Eleven, Elevendigit, bags, of, each, marked, Probability, of, (or)(or), more = from =their 11., n wheat, A=, 9flour,, 407km, Whosedistance, distance, 7km, bags, of, wheat, flour,, each, marked, Probability, = 3Eleven, 11., bags of wheat flour,, whose, within, 1/2 more, km nfrom, (S) work, 40, 40 11. Eleven, 246,, 369,, 789,, 999,, 444,, 123,, 432, and, 153., (, ), 5, kg,, actually, contained, the, following, 4.97, 5.05, 5.08, 5.03, 5.00, 5.06, 5.08, 4.98, 5, kg,, actually, contained, the, following, S, 15 5the, work, place, isbe, 31., n(B) =female, 31, 5 kg, actuallyn contained, following, iii., Let, ‘c’, event, engineers, 5, kg,, actually, contained t, place, is, 0, n(c), =, 0, iii., Let, ‘c’, be, event, female, engineers, iii. Let ‘c’31be event female, engineers, iii. Let, ‘c’ be eventweights, female, engineers, n(A), = 9of, &, n(s) = 15, flour(inkg):, 5.04, 5.07, 5.00, weights, of, flour(inkg):, nfrom, B ) work, weights, of, flour(inkg):, = of within, (, whose, distance, within, 1/2, km, from, weights, of, flour(inkg):, whose, distance, within, 1/2, km, work, 1, Probability, km, 11. Eleven, bags, ofwork, flour,, marked, whose, distance, within, km, work within, (5.03, whose, 1/2 km, from, 4.97, 5.05, 5.08, 5.03, 4.98, = fromdistance, Probability, of 7km, (or)21/2, more, nwheat, A ) 5.00, 9 5.06, 3each, Find, the, probability, that, any5.08, of, these, 4.97, 5.05, 5.08, 5.00, 5.06, 5.08, 4.98, 40, 4.97, 5.05, 5.08, 5.03, 5.08, place, 4.97following, 5.054.98, 5.08 5.03 5.00 5., placeis, is000n(c), n(c)=, =000, Probability, =, = 5.00, = 5.06, n (is, S)0 n(c) = 0, 5bags, kg,5.07, actually, contained, the, place, is, n(c), =, place, 5.04, 5.00, chosen, at, random, contains, more, 5.04, 5.07, 5.00, n ( S) 15 5.04, 5 5.07 5.00, n (Let, c ) ‘c’0 be event11 female engineers, iii., 5.04, 5.07, 5.00, Probability, of, within, km, Probability, of, within, km, weights, ofprobability, flour(inkg):, =whose, = =, 31 0within1 21/2, that, than, kg, of, flour., Find, the, probability, that any, any of, of these, these, Probability, km Probability, of within 1Find, km 5the, from work, Find, the, probability, that, any, of, Find, thethese, probability that, =40of within, n ( s )distance, 22 km, 2Eleven, 11., bags, of, wheat, flour,, each, marked, 4.97, 5.05, 5.08, 5.03, 5.00, 5.06, 5.08, 4.98, bags, chosen, at, random, contains, more, Ans., Total, number, of, bags, of, wheat, flour, is, 11., bags, chosen, at, random, contains, more, nn((ccis)) 0 n(c), place, 0040= 0, bags, chosen, at, random, contains, more, bags, chosen, at random co, n, c, (, ), n, c, 0= 00, (, ), 0, =, =, =, =, =, 5, kg,, actually, contained, the, following, 5.04, 5.07, 5.00, than, 5, kg, of, flour., \n(s), =, 11, than, 5, kg, of, flour., =, 0 event, 1frequency, =, =, = 0, iii.nn(Let, ‘c’, be, female, engineers, than 5 kg of flour., than 5 kg of flour., s=, 40, Probability, of, within, km, 9. =Activity, :, Note, the, of, twos, 40, ), (, ), weights, n ( s ) 40, 2, Find, the, any, of, these, Ans., of, of, wheat, flour, 11., nfrom, 40, Let, beofprobability, aflour(inkg):, event, number, of is, Ans. Total, TotalAnumber, number, ofbags, bagsof, ofthat, wheat, flour, 11., ( s ) fourwhose, distance, within 1/2 kmand, work, Ans., Total, number, of, bags, of, wheat, flour, isisbags, 11., Ans., Total, number, of bags of whe, wheelers,, three-wheelers, 4.97, 5.05, 5.08, 5.03, 5.00, 5.06, 5.08, 4.98, bags, chosen, at, random, contains, more, \n(s), =, 11, containing, wheat, flour, more, than, 5kg, is, 7, \n(s), =, 11, n ( cis, ) 0::n(c), 0going, place, =0 0the, \n(s) = 11, \n(s) = 11, 9., Activity, Note, frequency, of, twowheelers, past, during, a, time, 9., Activity, Note, the, frequency, of, two=, =, =, 9., Activity : Note the frequency, of two5.04, than, 55.07, kg, ofof, Let, be, aaflour., event, 9., Activity, : Note the frequency, two\n(A), 75.00, Let A, be, event of, of number, number of, of bags, bags, n ( s ) in, 40of, Let, AA =be, a event, of, number, Let Aofbebags, a event of num, wheelers,, three-wheelers, and, interval,, front, of 1your, gate., wheelers,, three-wheelers, and fourfourProbability, within, km school, wheelers,, three-wheelers, and, fourFind, the, that, any, of, Ans. Total, number, of, bags, ofmore, wheat, flour, isthese, 11., containing, wheat, flour, than, 5kg, isis, 77, three-wheelers, andprobability, fourProbability, of, wheat, flour, bags, containing, wheat, flour, more, than, 5kg, 2 wheelers,, containing wheat flour morecontaining, than 5kg iswheat, 7, flour more, wheelers, going, past, during, aa time, Find, the, probability, that, any, one, wheelers, going, past, during, time, wheelers, going, past, during, a, time, bags, chosen, at, random, contains, more, \n(s), =, 11, \n(A), =, 7, wheelers, going, past, during, a, time, \n(A), =, 7, n, c, (, ), 0, n, A, 9., Activity, :, Note, the, frequency, of, two(, ), 7, \n(A), =, 7, \n(A), =, 7, interval,, in, front, of, your, school, gate., vehicle, out, of, the, total, vehicles, you, have, interval,, in, front, of, your, school, gate., =interval,, = in=front, 0 of yourinterval,, school fourgate., than, kg, of, morethan, 5ks, =, Probability, wheat, flour, bags, A5school, be=, aof, event, of, number, in front of Let, your, gate., Probability, offlour., wheat, flour, bags of bags, wheelers,, of, wheat, bags, Probability of wheat flour bag, n ( s )the, Find, probability, that, any, one, observed, aprobability, two-wheeler., Find, theis40three-wheelers, thatand, any one, one Ans. Probability, nflour, 11, (Sflour, ) ofmore, Find, the, probability, that, any, Total, number, of, bags, wheat, flour, containing, wheat, 5kgisis11., 7, Find, the, probability, that, any, one, nn((AA)) 77 than, wheelers, going, past, during, a have, time, vehicle, out, of, the, total, vehicles, you, Ans. Let, the, frequency, of, types, of, wheeler, after, vehicle, out, of, the, total, vehicles, you, have, n, A, ( ) 7, n (A) 7, \n(A), ==, 7=, morethan, 5ks, =, vehicle, out, of, the, total, vehicles, you, have, \n(s), =, 11, morethan, 5ks, =, vehicle, out, of, the, total, vehicles, you, have, morethan, =, 5ks n=, in, of, your, gate., morethan, =, 5ks, 9. interval,, Activity, :isisNote, twoobserved, a(ie.,, two-wheeler., school, time, 4the, pmfrequency, to 4 –school, 45)offor, 45 12. In, observed, afront, two-wheeler., 11, Q.5,, Exercise, 14.2,, were, asked, to =, n((S, Sflour, 11, )))ofyou, observed, is, a, two-wheeler., Let, A, be, a, event, number, of, bags, Probability, of, wheat, bags, n, S, 11, observed, is, a, two-wheeler., (, n ( S) 11, Find, probability, any fourone, wheelers,, three-wheelers, and, Ans., Let, the, frequency, of, types, of, wheeler, after, minutes., Ans.Let, Let, thethe, frequency, oftypes, typesthat, ofwheeler, wheeler, after, prepare, a frequency, distribution, table,, Ans., the, frequency, of, of, after, containing, wheat, flour, more, than, 5kg, is, 7, Ans., Let, the, frequency, of, types, of, wheeler, after, ( A ) you, 7 were, n14.2,, vehicle, out, of(ie.,, the44total, you, have, wheelers, going, past, afor, time, school, time, pm, to, 4 –– of, 45), 45, school, time, (ie.,, pm vehicles, toduring, 45), for, 45 12., In, Q.5,, Exercise, the, of asked, sulphur, 12., In, Q.5,, Exercise, 14.2,, you, were, askedto, to, morethan, =, =, Types time, of, wheeler, Frequency, wheeler, school, (ie.,, 4 pm, to, 44school, – 45), for, 45, \n(A), 75ks, In, Exercise, 14.2,, you, were, asked, to, time, (ie., 12., 4 pmregarding, toQ.5,, 4 –=, 45), forconcentration, 45, 12., In Q.5,, Exercise, 14.2, you w, observed, is, a, two-wheeler., n, S, 11, interval,, in front of your school gate., (, ), minutes., minutes., prepare, a, frequency, distribution, table,, dioxide, in, the, air, in, parts, per, million, of, a, prepare, a, frequency, distribution, table,, Probability, of wheat flour, bags, minutes., prepare, a, frequency, distribution, table,, minutes., prepare, a, frequency, distri, 2, wheeler, 150, Ans. Let, the frequency, of types of, wheeler, after, Find, the, probability, that, any, one, regarding, sulphur, certain, citythe, forconcentration, 30 days. Usingof, this, table,, regarding, the, concentration, of, sulphur, Types, of, wheeler, Frequency, of, wheeler, Types, of, wheeler, Frequency, of, wheeler, regarding, the, concentration, of, sulphur, regarding, the, concentratio, 3, wheeler, 30, Types time, of, wheeler, Frequency, wheeler, of, wheeler, of, wheeler, ( Aparts, ) you, school, (ie.,, pm, to, 4 Types, – of, 45), forhave, 45 12.Frequency, In, Q.5,, were, askedof, vehicle, out, of, the4total, vehicles, you, dioxide, in, the, air, in, million, aa, find, theExercise, probability, of, the7per, concentration, dioxide, in, the, airn14.2,, in, parts, per, million, ofto, morethan, =, 5ks, =, dioxide, in, the, air, in, parts, per, million, of, dioxide, in, thea air in parts pe, 2, wheeler, 150, 4, 70, 2, wheeler, 150, minutes., prepare, a, frequency, distribution, table,, observed, is a two-wheeler. 1502 wheeler, 2 wheeler, n days., Sin) the, 11, 150, certain, city, for, 30, Using, this, (, of, sulphur, dioxide, interval, 0.12certain, city, for, 30, days., Using, this, table,, certain, citythe, forconcentration, 30 days. Using, table,, certain, city, for 30 days. Usi, 3 wheeler, 30, wheeler, 30 150 after, No.ofoftwo, wheeler, 3, regarding, ofthis, sulphur, Ans. Let, the, frequency, types, of=, wheeler, 33wheeler, 30, wheeler, 30, find, probability, 0.16, on, any, of these of, days., findthe, the, probability, ofthe, theconcentration, concentration, Types, of, wheeler, Frequency, of3wheeler, Probability, =, =, find, the, probability, of, the, concentration, find, the, probability, of the c, 4, wheeler, 70, 4, wheeler, 70, Total, wheelers, 5 Ans., in, the, airdays, in, parts, million, of to, a, school, time (ie.,, 4 pm, to 4 –7045), for 45, 42 wheeler, 12. dioxide, In, Q.5,, Exercise, 14.2,, you, were, 4 250, wheeler, 70, of, dioxide, in, interval, Total, number, of, = the, 30., n(s), = asked, 30 0.12of sulphur, sulphur, dioxide, in, theper, interval, 0.12wheelerNo.of, 150, of, sulphur, dioxide, in, the, interval, 0.12of, sulphur, dioxide, in, the i, No.of two, twowheeler, wheeler 150, 150 3, for, 303which, days., Using, this table,, minutes., prepare, adays, frequency, distribution, table,, two, wheeler, 150, 33No.of twocertain, 0.16, on, any, of, days., Number, of, on, the concentration, 0.16, oncity, any, ofthese, these, days., wheeler, 150, Probability, == No.of, =, =, Probability, =, =, Total, going, =, n(s), =, 250, 3number, wheeler, 30, 0.16, on, any, of, these, days., 0.16, on, any, of, these, days., Probability, = wheeler, =, =, Probability, =probability, =concentration, Total, 250, Totalwheelers, wheelers, 250 =5, find, the, the, concentration, regarding, the, of, sulphur, Ans., Total, number, of, days, ==0.09, 30., ==30, 0.03, 0.08, 0.04, 0.17 of, sulphur, dioxide, in, the, interval, Ans.wheelers, Total, number, of0.08, days, 30.n(s), n(s), 300.12, Total, wheelers, 250, Number, ofwheeler, 2 wheelers, going =70n(A), = 15055 Total, 250, 5is of, Types, of, Frequency, of wheeler, 4 wheeler, Ans., Total, number, of, days, =Ans., 30., n(s), 30, Total= number, of days = 30. n, of, sulphur, dioxide, in, the, interval, 0.12dioxide, in, the, air, in, parts, per, million, of a, Number, of, days, on, which, the, concentration, 0.16, is, 2, ., n(A), =, 2, Number, of, days, on, which, the, concentration, Total, number, wheeler, going, =, n(s), =, 250, Total, number, wheeler, going, =, n(s), =, 250, 0.16, 0.05, 0.02, 0.06, 0.18, 0.20, No.of, two, wheeler, 150, 3, Number, of, days, on, which, the, concentration, 2, wheeler, 150, Number, of, days, on which the, Total, number, wheeler, going, =, n(s), =, 250, Total number, = n(s), =for, 250, 10. Activity : Ask all the students, in yourwheeler going, 0.16, on, any, these, certain, city, 30isdays., Using, this, table,, of, sulphur, dioxide, in, the, interval, -Probability, ofof, sulphur, dioxide, 0.12, − 0.12, 0.16, of0.11, sulphur, dioxide, isdays., in, the, interval, 0.12, Probability, =, Number, of, going, ==30, n(A), ==150, Number, of22=2wheelers, wheelers, going=, n(A), 150, 0.08, 0.12, 0.13, 0.22, 0.07, of, sulphur, dioxide, is, in, the, interval, 0.12, 3, wheeler, of, sulphur, dioxide, is in the i, Number, of, wheelers, going, =, n(A), =, 150, Total, wheelers, 250, 5, Number, of 2 wheelers, going, =2n(A), =of=, 150, class to write a 3-digit number., Choose, Ans. Total, number, days, = 30., = 30, find, the, then(s), concentration, 0.16, is, .0.01, 22 of, 0.16, is, 2probability, .n(A), n(A), =, n, A, (, ), 0.08, 0.10, 0.06, 0.09, 0.18, 2, 1, 0.16, is, 2, ., n(A), =, 2, 4, wheeler, 70, 0.16, is, 2, ., n(A), =, 2, 10., :: Ask, all, the, students, in, any, student, from, at random., 10. Activity, Activity, Ask, allthe, theroom, students, in your, your, on which, theinterval, concentration, of, sulphur, dioxide, indioxide, the, 0.12=Number, =of days, =, Probability, of, sulphur, 0.12, 10., Activity, : Ask, all, the, students, your, Probability, of, sulphur, dioxide, 0.12−−0.16, 0.16, 10., Activity, : Ask all the, students, in, your, Total, number, wheeler, going, = n(s)in, = 250, Probability, of, sulphur, dioxide, 0.12, 0.16, Probability, No.of, two, wheeler, 150, 3, 0.11, 0.07, 0.05is in, 0.07, 0.01 − 0.12, 0.04of- sulphur dioxid, class, to, write, a, 3-digit, number., Choose, n, s, 30, 15, What, is, the, probability, that, the, number, class, to, write, a, 3-digit, number., Choose, (, ), of, sulphur, dioxide, the, interval, on, any, of, these, days., Number, of 2=wheelers, =, n(A), =write, 150 a 3-digit0.16, class, to write, a 3-digitgoing, number., Choose, Probability, =, =, class, to, number., Choose, nn((AA)) 22 11, any, from, the, at, written, by her/him, isroom, divisible, by 3?5 Ans., any student, student, from, the, room, at random., random., Total, wheelers, 250, n (is, Anumber, )2at. n(A), 2=of=1days, 2 = 30. n(s)n (=A30, ) 2 1, =, =, =, Total, =0.16, =, student, from, the, room, at, random., any, student, from the, room, random., =, =, =, =, = =, 10. any, Activity, :, Ask, all, the, students, in, your, n, s, 30, 15, What, isisthe, probability, that, the, number, n, s, 30, 15, Remember, that, a, number, is, divisible, by, What, the, probability, that, the, number, (, ), (, ), Probability, of, sulphur, dioxide, 0.12, −, Number, of30, days 15, on which the concentration, n ( s )the, What, is write, the probability, thatWhat, number, Total to, number, wheeler, going, =the, n(s), 250probability, n ( s ) 0.16, 30 15, is=the, that, number, class, a 3-digit, Choose, written, by, her/him, isisnumber., divisible, by, 3?, written, by, her/him, divisible, by, 3?, 185, of ndivisible, sulphur, dioxide, is in the interval 0.12 written, by, her/him, is, divisible, by, 3?, Number, of, 2, wheelers, going, =, n(A), =, 150, written, by, her/him, is, by, 3?, A, (, ), 2, 1, any, studentthat, from, the, room, at, random., Remember, aanumber, isisdivisible, by, Remember, that, number, divisible, by, =0.16 is, =, is=, 2 . n(A), =by, 2, Remember, that, a number, is, divisible, by, Remember, that a number, divisible, n, s, 30, 15, is, the, probability, that, the, number, (, ), 10. What, Activity, :, Ask, all, the, students, in, your, 3, if the sum of its digits is divisible by 3., Probability of sulphur dioxide 0.12 − 0.16, n 7km, by, her/him, is number., divisible, by, 3?, classthetonumber, write, aof3-digit, Choose, Ans. written, Let, students, in is 15., Three, n (A) 2, 1, Remember, that, a, number, is, divisible, by, any, student, from, the, room, at, random., digits numbers written by each are 124,, =, = =, n, s, 30, 15, What, is, the, probability, that, the, number, (), 136, 135, 246, 369, 562, 789, 999, 444,, written, by, her/him, is 153., divisible by 3?, 256,, 123,, 569,, 721,, 432,, engineers., Remember, that a number, is by, divisible, by, Three digit numbers, divisible, 3 are 135,, e from their, 246, 369, 789, 999, 444, 123, 432 and 153.

Page 191 :
186, Chapter, 186 15 – Probability, 186, , 13., Q.Q.1,1,Exercise, 13. In, Exercise14.2,, 14.2,you, youwere, wereasked, asked, 186, 13., InInQ., 1, Exercise, 14.2,, you, were, asked, to, prepare, a, frequency, distribution, to, prepare, a, frequency, distribution, to prepare, a frequency, distribution, table, regarding, the, groups, ofof, table, regarding, theblood, blood, groups, 13. In, Q. 1,, Exercise the, 14.2,, you were, asked, table, regarding, blood, groups, of, 3030students, of, a, class., Use, this, table, studentsofaofafrequency, aclass., class.Use, Usethis, thistable, tableto, to, prepare, distribution, 30, students, toto, determine, the, probability, that, a astudent, determine, the, probability, that, student, table, regarding, the, blood, groups, of, determine, the probability, a student, of, selected, atatthat, random,, has, ofthis, thisclass,, class,, random,, has, 30, students, of selected, aselected, class. Use, this, tablehas, to, of, this, class,, at, random,, blood, group, AB., blood, group, AB., determine, the, probability, that, a, student, bloodnumber, group AB., Ans., ofofstudents, isis3030n(s), Ans.Total, Total, number, students, n(s)=, =30, 30, of, this, class,ofselected, at, random,, Ans., Total, number, students, is 30, n(s), =blood, 30has, Let, the, number, of, students, having, Let, the, number, of, students, having, blood, blood, group, AB., A,B,0,0,AB,0,A,0,B,A,0,B,A,0,0,A,AB,0,, Let theAB, number, of =, students, having blood, group, 3 3n(A), 3, group, ABis, n(A), Ans. A,A,0,0,AB,B,A,0,B,A,B,0, Total, number, students, = 30, group, AB, isis3of, n(A), = =3 3 is 30 n(s), n (nA( A, )), Let, the, number, of, students, having, Probability, ofofblood, group, AB, = =n ( Ablood, ), Probability, blood, group, AB, Probability, blood=group, group, AB isof3 n(A), 3 AB = n (ns()s ), n (s ), n (A), 33 11, Probability, blood, group, AB, =, 0.1, == of, =, =, 3 = 1 = 0.1, n (s ), = 30, = 10, = 0.1, 3030 1010, 3, 1, 0.1, = = = Problems, Additional, Additional, Problems, 30 10 Problems, Additional, I.I., I., 1.1., 1., I., 2., 1.2., 2., 2., , 3.3., 3., 4., 3.4., 4., 5., 4.5., 5., 5., 6.6., 6., 6., 7.7., 7., 7., , Multiple, Choice, Multiple, ChoiceQuestions, Questions, Additional, Problems, Multiple, Choice, Questions, The, minimum, probability, ananevent, Theminimum, minimumprobability, probabilityof, eventis, The, ofof, anInfinity, event, isis, a), 1, b), 0, c), –1, d), Multiple, Choice, Questions, a), 1, b), 0, c), –1, d), Infinity, a) 1, b) 0, c) –1, d) Infinity, A, die, isisthrown, once,, a anumber, The, minimum, probability, of anisevent, is, A, die, thrown, once,, number, isnoted,, noted,, A, die, is thrown, once,c)athat, number, is, noted,, then, probability, it, is, a, prime, a)then, 1 the, b), 0, –1, d), Infinity, theprobability, probabilitythat, thatititisisa aprime, prime, then the, number, isis, number, A die is thrown, is noted,, number, is 4 once,2 a number, 3, 4 c) 2 2that d)it 11is1 a prime, then, probability, a)a)3 3the b), 4, a) 6 6 isb)b)6 6 c)c)6 6 d)d)6 6, number, 6, 6, 6, 6, 3, 4, 2, 1, Probability, is, a)Probability, b) ofofanansure, c)sureevent, d), eventisis, Probability, event, 6of 1an sure, 6c) 1/2, 6 100%, a), 060, b), a), b), 1, c), 1/2 d), 100%, a) 0, b) 1, c) 1/2, d)d)100%, Probability, of, an, impossible, event, sure, event, is, Probabilityofofananimpossible, impossibleevent, eventis, Probability, isis, a), 1, b), 1/2, c), 100, d), 1/2, 0, 1, 1/2, 100%, a), 1, b), 1/2, c), 100, d), 1/2, a) 1, b) 1/2 c) 100 d) 1/2, The, sum, of, Probability, ofallan, impossible, event of, is all, Thesum, sumofof, allthe, theprobabilities, probabilities, The, all, the, probabilities, ofofallall, these, outcomes, of, a, trail, is, 3, a)these, 1 possible, b), 1/2, c), 100, d), 1/2, possibleoutcomes, outcomesofofa atrail, trailisis, these, a), 0 0 possible, b)b)1 1 c)c)–1–1, d)d)1/2, a), 1/2of all, The, sum, of, all, the, probabilities, a) 0, b) 1, c) –1, d) 1/2, P(E), +, P(E), is, these, possible, outcomes, of, a, trail, is, P(E)+ +P(E), P(E)isis, P(E), a), 0, b), 1, c), –1, d), 1/2, a)a)02 0, b), b)2 2+ P(E)1 is, P(E), b), c), 11, b) 2, a)c)100 , c), d), None, these, Noneof, these, c)d)None, d) None of these, b), 21 , d), ofofthese, In, there, c)In, 1a aclass, classthere, thereare, arexx xboys, boysand, andyy ygirls,, girls,, In, a class, are, boys, and, girls,, A, is, selected, at, random,, then, d)Astudent, None, of, these, student, is, selected, at, random,, then, A student isof selected, at, random,, probability, selecting, a agirl, isis then, probability, of, selecting, girl, In, a, class, there, are, x, boys, and, y, girls,, probability of selecting a girl is, A student is selected at random, then, probability of selecting a girl is, , IXIXStandard, 189, Standard–– –Mathematics, Mathematics, IX Standard, Mathematics, x, xx, y, y, Standard, a)a)x x b)IX, c)c)y y – Mathematics, d)d) y y, x, b), a) y y b) x x+ +y y c) x x d) x x+ +y y, y, x+y, x, x+y, x, y, y, Ans., 1)1)bxb, Ans., a), b), c), d), Ans. 1), 2)2)baya, x+y, x, x+y, 2) ba, 3), 3), b, Ans. 1), 3) bdb, 4), 2)4)da dc, 4), 5), b, 3)5)bb b, 5), 6), c, 4)6)cd c, 6), 7), d, 5)7)db d, 7), 6) c, II.II.Answer, the, Answer, thefollowing, followingquestions, questions, 7), d, II. Answer, the, following, questions, 1.1. AAfair, times, faircoin, coinis, istossed, tossed60, 60questions, timesand, andit, the, following, 1.II. Answer, A fair, coin, is, tossed, 60, times, and, itit, came, up, with, tails, 27, times., Find, the, came, up, with, tails, 27, times., Find, the, came up with, tails 27 times. Find the, probability, ofofhead., probability, head., 1. A, fair coinofis, tossed 60 times and it, probability, head., Ans., Total, out, comes, n(s), Ans., Total, out, comes, n(s)=, =60, 60, came, up, with, tails, times. Find the, Ans. Total, outof, comes, n(s), ==27, 60, Number, tails, n(T), 2727, Number, of, tails, n(T), =, probability, of, head., Number of, of heads, tails n(T), = =2760 – 27 = 33, Number, n(H), Number, ofheads, heads, n(H), =6060– –2727= =3333, Ans. Total, out of, comes, n(s), = 60, Number, n(H), =Number, heads, Numberof, heads, Number, of, tails, n(T), =, 27, Probability, of, head, =, Number, ofofheads, Probability, of, head, =, Total, no.of, out, Probability, of head, = Total, Number, of heads, n(H), = 60 –no.of, 27 =out, 33comes, comes, Total no.of out comes, 3333, 1111Number of heads, = =33, ( or( or) =)11, Probability, of head, = 6060( or, no.of out comes, ) 20Total, 60, 2020, 33 Find, 11, 2.2. AAdie, =thrown., ( orFind, )Findthe, dieis, isthrown., theprobability, probabilityofof, 2. getting, A die, isan, thrown., 60, 20 the probability of, odd, number., gettingananodd, oddnumber., number., getting, Ans., A, die, isisthrown, total, out, Ans., A, die, thrown, total, outcomes, comesare, are, 2., A, die, is, thrown., Find, theout, probability, of, Ans. 1,2,3,4,5,6, A die is \n(s), thrown=, total, comes, are, 6, 1,2,3,4,5,6, \n(s), =, 6, getting, an, odd, number., 1,2,3,4,5,6, \n(s) getting, =6, A, odd, Adie, dieis, isthrown, thrown, getting, oddnumber, numberare, are, Ans. A, die, is, throwngetting, total odd, out, comes, are, A, die, is, thrown, number, are, 1,3,5, n(A), =, 3, 1,3,5, n(A), =, 3, 1,2,3,4,5,6, \n(s), =, 6, 1,3,5 n(A) = 3, n ( A( A, )), A, die is thrown, getting, odd, number, are, = =n n( A, Probability, ofofgetting, odd, number, ), Probability, getting, odd, number, Probability, 1,3,5, n(A) =of3 getting odd number = n (ns()s ), n (s ), 3 3 n (A), =, Probability of getting odd number, = =3 6 6 = n ( s ), 6, 3.3. Two, coins, tossed, simultaneously,, Find, Twocoins, coinstossed, tossedsimultaneously,, simultaneously,, Find, =3, 3. the, Two, Find, 6 or more, probability, of, getting, one, the, probability, of, getting, one, or, more, the probability of getting one or more, tail., tail.coins tossed simultaneously, Find, 3. tail., Two, Ans., Total, number, ofof, out, comes, (HH,HT,TH,TT), Ans., Total, number, out, comes, (HH,HT,TH,TT), the probability, ofcomes, getting, one or more, Ans. Total, number, of out, (HH,HT,TH,TT), n(s), =, 4, n(s), =, 4, tail. = 4, n(s), AAbebeevent, one, eventgetting, getting, one(or), (or)more, moretail, tailare, are, Ans. Total, of, out comes, (HH,HT,TH,TT), A be number, event, getting, one, (or), more, tail, are, (HT,TH,TT), n(A), =, 3, (HT,TH,TT), n(A), =, 3, n(s) = 4, (HT,TH,TT), n(A) = 3, A be event getting one (or) more tail are, (HT,TH,TT) n(A) = 3

Page 192 :
190 15 – Probability, Chapter, , IX Standard – Mathematics, 187, , Probability of getting one (or), more tail =, , n (A), n (s ), , =3, 4., , 4, , Two dice are thrown simultaneously, 500 times. Each time the sum of two, numbers. Appearing on their tops is, noted and recorded as given in the, following table., , Sum, , 2, , 3, , 4, , 5, , 6, , 7, , 8, , 9, , 10, , 11, , 12, , Frequency, , 14, , 30, , 42, , 55, , 72, , 75, , 70, , 53, , 46, , 28, , 15, , Ans., , Find probability of getting, a) Sum 3, b) Sum more than 10, c) Sum less than (or) equal to 5, d) Sum between 8 and 12, 2, a) Probability of getting a sum 3, 30, = = 0.6, 500, b) Probability of getting sum, 28 + 15 43, =, = = 0.086, more than10, 500, 500, c) Probability of getting sum less than 5, 14 + 30 + 42 + 55 141, =, (or) equal to 5 =, 500, 500, = 0.282, d) Probability of getting sum between, 8 and12 =, , 53 + 46 + 28 127, = = 0.254, 500, 500

Page 193 :
191, 191, , Appendix, Appendix, , Appendix, Appendix -- 22, Appendix, -2, Introduction, to, Modeling, Introduction, to Mathematical, Mathematical, Modeling, Introduction to Mathematical Modeling, A2.1, 1.Exercise, Suppose, a company needs a computer, for some period of time. The company, 1., Suppose a company needs a computer, can either hire a computer for ? 2,000, for some period of time. The company, per month or buy one for ? 25,000. If the, can either hire a computer for ? 2,000, company has to use the computer for a, per month or buy one for ? 25,000. If the, long period, the company will pay such, company has to use the computer for a, a high rent, that buying a computer, long period, the company will pay such, will be cheaper. On the other hand, if, a high rent, that buying a computer, the company has to use the computer, will be cheaper. On the other hand, if, for say, just one month, then hiring, the company has to use the computer, a computer will be cheaper. Find the, for say, just one month, then hiring, number of months beyond which it will, a computer will be cheaper. Find the, be cheaper to buy a computer., number of months beyond which it will, Ans. Step : 1 - Formulation, be cheaper to buy a computer., The relevant factors are the time period for, Ans. Step : 1 - Formulation, hiring a computer, and the two costs given, The relevant factors are the time period for, to us. We assume that there is no significant, hiring a computer, and the two costs given, change in the cost of purchasing or hiring, to us. We assume that there is no significant, the computer. So, we treat any such change, change in the cost of purchasing or hiring, as irrelevant. We also treat all brands and, the computer. So, we treat any such change, generations of computers as the same i.e.,, as irrelevant. We also treat all brands and, these differences are also irrelevant., generations of computers as the same i.e.,, The expense of hiring the computer for x, these differences are also irrelevant., months is Rs 2000x. If this becomes more, The expense of hiring the computer for x, than the cost of purchasing a computer, we, months is Rs 2000x. If this becomes more, will be better., than the cost of purchasing a computer, we, 2000x = 25000 ...(1), will be better., Step 2 : Solution : Solving (1), 2000x = 25000 ...(1), 25000, Stepx2 : Solution, Solving (1), =, = :12.5, 2000, 25000, =, 12.5 : Since the cost of, Stepx 3 :=, Interpretation, 2000, hiring a computer becomes more after 12.5, Step 3 : Interpretation : Since the cost of, months, it is cheaper to buy a computer, if, hiring a computer becomes more after 12.5, you have to use it for more than 12 months., months, it is cheaper to buy a computer, if, 2. you, Suppose, car itstarts, from, a place, A and, have toa use, for more, than, 12 months., travels at a speed of 40 km/h towards, 2., Suppose a car starts from a place A and, another place B. At the same instance,, travels at a speed of 40 km/h towards, another car starts from B and travels, another place B. At the same instance,, another car starts from B and travels, , towards A at a speed of 30 km/h. If the, distance between A and B is 100 km,, towards A at a speed of 30 km/h. If the, after how much time will the cars meet?, distance between A and B is 100 km,, Ans. Step 1 : Formulation, after how much time will the cars meet?, We will assume that cars travel at a, Ans. Step 1 : Formulation, constant speed. So, any change of speed, We will assume that cars travel at a, will be at a distance of (100 - 30x)km from, constant speed. So, any change of speed, A. So the equation will be 70x = 100, will be at a distance of (100 - 30x)km from, i.e., 70x = 100, A. So the equation will be 70x = 100, Step 2 : Solving equation, we get, i.e., 70x = 100, 100, Step, x = 2 : Solving equation, we get, 70, 100, x=, 100, Step70, 3:Interpretation, is, 70, 100, Step, 3:Interpretation, is, approximately, 70, 1.4 hours.So, the car will meet after, approximately, 1.4hours.So,, hours the car will meet after, 1.4, 1.4, Thehours, moon is about 3,84,000 km from the, earth, and its path around the earth is, 3., The moon is about 3,84,000 km from the, nearly circular. Find the speed at which, earth, and its path around the earth is, it orbits the earth, assuming that it, nearly circular. Find the speed at which, p = 3.l4), orbits the earth in 24houra(Use7i, it orbits the earth, assuming that it, Ans. Step 1 : Formulation : The speed at which the, orbits the earth in 24houra(Use7i = 3.l4), Length of the orbit, Ans. Step, 1 :orbits, Formulation, The, moon, the earth, earth: is, is= speed at which the, Time, Length, of taken, the orbit, moon orbits the earth is, Step 2 : Since the orbit isTime, nearly, circular, taken, the length is 2 x p x 384000 km = 2411520, Step 2 : Since the orbit is nearly circular, km. The moon takes 24 hours to complete, the length is 2 x p x 384000 km = 2411520, one orbit. So, km. The moon takes 24 hours to complete, 2411520, one, orbit. =, So, Speed, 100480 km / hr, =, 24, 2411520, Speed, 100480: km, / hrspeed is, =, Step 3 :=, Interpretation, The, 24, 100480 km/hr., 192Step, 3 : Interpretation : The speed is, 4. 100480, A family, pays Rs 1000 for electricity on, km/hr., an average in those months in which, 4., Ait family, paysuse, Rsa1000, forheater., electricity, on, does not, water, In the, months in which it uses a water heater,, the average electricity bill is Rs 1240., The cost of using the water heater is Rs, 8.00 per hour. Find the average number, 3., , (ii) T, in the, (iii), vehic, and f, moto

Page 194 :
192, 192an, , average in those months in which, it does not use a water heater. In the, months in which it uses a water heater,, the average electricity bill is Rs 1240., The cost of using the water heater is Rs, 8.00 per hour. Find the average number, of hours the water heater is used in a, day., Ans. Formulation : An assumption is that the, difference in the bill is only because of, using the water heater., Let the average number of hours for which, the water heater is used = x., Difference per month due to using water, heater = Rs 1240 – Rs 1000 = Rs 240, Cost of using water heater for one hour =, Rs 8, So, the cost of using the water heater for, 30 days = 8 x 30 x x, 192Also, the cost of using the water heater for, 30 days = Difference in bill due to using, an average, water, heater. in those months in which, it, does, use a water heater. In the, So, 240xnot, = 240, months, in, which, uses a water, Solution : From thisitequation, we getheater,, x = 1., the, average, electricity, bill, Rs water, 1240., Interpretation : Since x = 1,is the, The, cost, of, using, the, water, heater, is Rs, heater is used for an average of 1 hour, in, 8.00, per, hour., Find, the, average, number, a days., of hours the water heater is used in a, Exercise, A2.2, day.A2.3, Exercise, Ans. Formulation : An assumption is that the, 1., We, have given, the gold, difference, in solving, thethe, billtimings, is word, onlyofbecause, of, 1., How, are the, of, problems, medalists, in, the, 400, meter, race, from, using, the, water, heater., that you come across in textbooks, the, the event, wasofincluded, the, Let time, the average, number, for in, which, different, from, the hours, process, of, Olympics,, in, the, table, below., Construct, the water heatermodeling?, is used = x., mathematical, aDifference, mathematical, model due, relating, the years, per month, to using, Ans. We, have already, mentioned, thatwater, the, and, timings., Use, it, to, estimate, the, timing, heater, =, Rs, 1240, –, Rs, 1000, =, Rs, 240, formulation part could be very detailed, in, in, theof, next, Olympics., Cost, using, water, heater, fornot, onevalidate, hour =, real, life situations., Also,, we do, Year in word, Timing, (in seconds), Rs 8answer, the, problems., A part from, So,, the, cost, of, using, the, water, for, this1964, word problem be the52.01, case, in heater, real - life, 30, days, =, 8, x, 30, x, x, situations., 1968, 52.03, Also,, the cost of using the, water heater for, 1972, 2., Suppose, want in, to51.08, minimise, the, 30 1976, days =you, Difference, bill, due to using, 49.28at, waiting, time, of, vehicles, a, traffic, water, heater., 1980, junction, four roads.48.88, Which of these, So,1984, 240x of, = 240, 48.83, factors, are, important, and, which are, Solution, 1988 : From this equation, 48.65we get x = 1., not?, Interpretation, : Since x48.83, = 1, the water, 1992 of petrol., (i), Price, heater, is, used, for, an, average, 1996, 48.25 of 1 hour in, a days., 2000, 49.11, 2004, 49.41, Exercise A2.3, Ans., Try your self, 1., , How are the solving of word problems, that you come across in textbooks, , So, 240x = 240, Solution : From this equation we get x = 1., IX Standard, Interpretation, : Since x– Mathematics, = 1, the water, heater is used for an average of 1 hour in, IX at, Standard, Mathematics, (ii), The rate, which the– vehicles, arrive, a days., in the four different roads., (iii) A2.3, The proportion of slow-moving, Exercise, vehicles like cycles and rickshaws, vehicles, like cars, and, 1. and, Howfast, aremoving, the solving, of word, problems, motorcycle, that you come across in textbooks, Ans. The, importantfrom, factors are, and (iii) here, different, the(ii) process, of, (i), is not an important, mathematical, modeling?factor although, have already, an effectmentioned, on the number, of, Ans. itWecanhave, that the, vehicles, sold.part could be very detailed in, formulation, real life situations. Also, we do not validate, the answer in word problems. A part from, this word problem be the case in real - life, situations., 2., , Suppose you want to minimise the, waiting time of vehicles at a traffic, junction of four roads. Which of these, factors are important and which are, not?, IX Standard – Mathematics, (i) Price of petrol., (ii) The rate at which the vehicles arrive, in the four different roads., (iii) The proportion of slow-moving, vehicles like cycles and rickshaws, and fast moving vehicles like cars and, motorcycle, Ans. The important factors are (ii) and (iii) here, (i) is not an important factor although, it can have an effect on the number of, vehicles sold.

Page 195 :
193, , Model Question Paper, Max Marks : 90, , I., 1., 2., 3., 4., , 5., 6., , Time : 3 hr, , Multiple choice questions :, Decimal form of 36/100 is, a) 0.36 , b) 0.036, c) 3.6 , d) 36, 3, 2, Degree of the polynomial 2x +4x + 7x is, a) 0 , b) 1 , c) 2 , d) 3, In the given figure ‘x’ value is, a) 110o , b) 90o , c) 120o , d) 180o, Formula used to calculate the area of Rhombus is, 1, 1, a) v1 × v 2, b) d1 × d 2, 3, 2, 1, 1, c) v1 + v 2, d) d1 × d 2, 3, 3, , 12 x1 = 12, , x, , 60o, , Biggest chord of a circle is, a) Radius, b) Circumference, c) Diameter, d) Major arc, Heron’s formula to find the area of the triangle, a) s ( s − a )( s − b )( s − c ), b) s ( s − a ) + ( s − b ) + ( s − c ), c) s ( s + a ) + ( s + b ) + ( s + c ), , d) s ( s + a ) + ( s + b ) + ( s + c ), , 7., , Check which of the following is solution of equation x – 2y = 4, a) (0,2) , b) (2,0) , c) (4,0) , d) (0,4)p, 8. In figure, sides QP & RQ of DPQR are produced to point S & T respectively. If∟SPR, = 135o & ∟PQT = 110o then the measure of ∟QPR, P, a) 45o , b) 65o , c) 135o , d) 110o, 135o, 9. In quadrilateral one pair of opposite are parallel. It is a, 110o, a) Square, b) Centroid, c) In centre, d) Trapezium, T, R, Q, 10. Formula to find the mean value of grouped data is, ∑ fx, a) X =, b) ∑ fx = X × n, n, ∑ x3 ), (, ∑ fx, c) n =, d) X, x, n, 11. Two coins are tossed simultaneously 500 times, and we get two heads 105 times, then, the probability of occurrence of these events is, a) 0.31 , b) 0.21 , c) 0.41 , d) 0.51

Page 196 :
194, , IX Standard – Mathematics, , 12. Formula to find the total surface area of the cylinder is, a) pr(r + h) , b) 2pr(r + h), c) 2pr(r + 1), d) pr(r + 1), II. One mark questions, 8x1=8, 2, 13. Find the value of the polynomial, p(x) = 5x – 3x + 7 at x = 1, 14. Name the point where horizontal & the vertical lines intersect in the Cartesian plane?, 15. Write any one Euclid’s axioms, 16. State “Midpoint theorem”, 17. A circle divides the plane on which it lies, in, parts, o, 18. To construct an angle of 60 at the initial point of a given ray, 19. Find the curved surface area of a right circular cone whose slant height is 10cm &, base radius is 7cm., 20. “A square in rectangle and also rhombus” true or false, III. Two mark question, 18 x 2 = 36, 21. Verify whether x =–1,2 are Zeros of the polynomial p(x)= (x + 1) (x –2), 22. Simplify : (√11 – √7) (√11 + √7), 23. Write the following cube is expanded form : (2x +1)3, 24. In which quadrant or on which axis do each of the points (2,–5) (–4,2) (–3,0) & (0,1), 25. Write any two Euclid’s postulates?, 26. In the given figure, lines PQ and RS intersect each other at point O., If ∟POR : ∟ROQ = 5 : 7 , find all the angles, S, , P, O, R, , Q, , 27. Find the remainder obtained p(x) = x3 + 1 by x + 1, 28. The angles of quadrilateral are in the ratio 3 : 5 : 9 : 13. Find all the angles of the, quadrilateral., 29. Define :, a) SAS congruence rule, b) AAS congruence rule, 30. In the figure, if lines PQ and RS intersect at point T. Such that ∟PRT = 40o , ∟RPT, = 95o & ∟TSQ = 75o Find ∟SQT.

Page 197 :
195, , Model Question Paper, P, , T, , R, , 75o, , S, , Q, , 31. In the figure, If AB || CD, ∟APQ = 50 & ∟PRD = 127o . Find ‘x’ and ‘y’., o, , A, , P, 50, , o, , C, , Q, , x, , B, , y, 127o, R, , D, , 32. Write True or False : Give reasons for yours answer., a) A chord of a circle, which in twice as long as its radius, is a diameter of the circle, b) A circle is a plane figure, 33. If two equal chords of a circle intersect within the circle, prove that the segments of, one chord are equal to corresponding segments of the other chord., 34. By using Heron’s formula, calculate the area of an isosceles triangle with equal sides, having length 12cm and the perimeter is 30 cm., 35. The curved surface area of a right circular cylinder is 88cm2 and its height is 14cm., Find the radius of the base of the cylinder., 36. A coin is tossed 1000 times with the following frequencies, Head : 455 , Tail : 545, compute the probability for each event., 37. The following number if goals were scored by a team in a series of 10 matches, 2,3,4,5,0,1,3,3,4,3, Find mean, median and mode of these score, 38. Find the CSA and TSA of a cone radius 14 cm, IV. Three mark questions , 6 x 3 = 18, 39. Show that the bisectors of angles of a parallelogram form a rectangle, 40. ABCD is a quadrilateral in which P,Q and S are mid -points of the sides AB,BC,CD, and DA.AC is a diagonal. Show that :

Page 198 :
196, , IX Standard – Mathematics, , 1, i.SR ||ACandSR = AC, 2, ii.PQ = SR, iii.PQRSis a parallelogram, 41., 42., 43., 44., , 48., , A, , R, , P, , C, , Q, , B, , Show how √7 can be represented on the number line., Construct a triangle XYZ in which <y = 30o , <z = 90o and XY + YZ + ZX = 11cm., Factorize : 2x3 + x2 – 2x – 1, The following table gives the life time of 400 neon lamps, Lifetime (in hours), 300 - 400, 400 - 500, 500 - 600, 600 - 700, 700 - 800, 800 - 900, 900 - 1000, , V., 45., 46., 47., , D, , Number of lamps, 14, 56, 60, 86, 74, 62, 48, , a. Represent the given information with help of a histogram., b) How many lamps have a life time of more than 700 hours?, Four mark question : , 4 x 4=16, Represent 3.765 on the number line using successive magnification., Draw the graph of linear equation in two variables : 3 = 2x + y, A cylindrical pillar is 25cm radius & 305m in height. Find the cost of painting the, curved surface of the pillar at the rate of 12.50/m2., At Ramzan Mela, a stall keeper in one of the food stalls has a large cylindrical vessel, of base radius 15cm filled up to a height of 32 cm with orange juice. The juice is filled, in small cylindrical glasses of radius 3cm up to a height of 8cm and sold for Rs 3 each., How much money does the stall keeper receive by selling the juice completely?