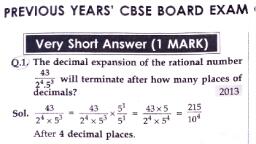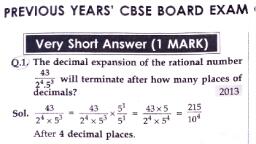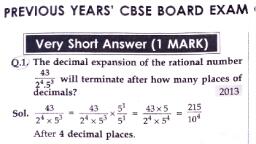Page 1 :
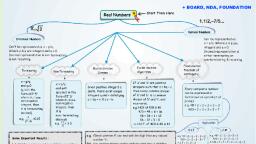
Page | 1, 1, NUMBER SYSTEMS, Samarth, EXERCISE 1.1, Classes, Q.1. Is zero a rational number? Can you write it in the form 2, where p and, q are integers and q + 0?, b, 0 0, Sol. Yes, zero is a rational number. It can be written as, 1'2, etc., in the form, 2, where p and q are integers and q # 0. Ans., q, Q.2. Find six rational numbers between 3 and 4., Sol. To find six rational numbers between 3 and 4 denominator should be, made equal to 6 + 1 = 7., 3x7, 21, 4x7, 28, Therefore,, 3 =, 7, 4 =, 7, 7, 7, Six rational numbers between 3 and 4 can be found by varying the, numerator between 21 and 28., 22 23 24 25 26 27, Or, the numbers are, 7, Ans., 7, 7, 7, 7, 4, and, 5, 3, Q.3. Find five rational numbers between, 4, Sol. To find five rational numbers between, and, we may add the given, numbers and divide by 2, and repeat the process., 3, 4, 7, 5 5, 7, = x1, 2, 5x2, 7+8, 10, 15, 7, 10, 10, 10, 15, 15, Next rational number =, X2, %3D, 10x2, 20, 4, +, 4, 15 + 16, 31, 20, 20, 31, 31, Next rational number =, x3, 20x2, 40, 31, 4, 31+32, 63, %3D, 40, 5, 40, 40, 63, 63, Next rational number =, = x4, 40x2, 80, 63, 4, 63 + 64, 127, 80, 80, 80, 127, 127, Next rational number =, X5, %3D, 80x2, 160, 3/4

Page 2 :
Page |2, 7, 3, 31, X3, 40, 63, 127, Ans., X1 =-, 10, 4', X5 =, 80, 160, (Note : Many answers are possible. There are of course infinitely many, rational numbers between, 3, and -.), Q.4. State whether the following statements are true or false. Give reasons for, your answers., (i) Every natural number is a whole number., (ii) Every integer is a whole number., (iii) Every rational number is a whole number., (i) True, since the collection of whole numbers contains all the natural, numbers and in addition zero., Sol., (ii) False. Negative integers are not whole numbers., 2 3 -3, (iii) False. Numbers such as =,, 3'4' 5, etc., are rational numbers but not, whole numbers.

Page 3 :
Page | 1, 1 |, NUMBER SYSTEMS, EXERCISE 1.2, Q.1. State uwhether the following statements are true or false. Justify your, answers., (i) Every irrational number is a real number., (ii) Every point on the number line is of the form Im, where m is a, natural number., (iii) Every real number is an irrational number., (i) True. All irrational and rational numbers together make up the, collection of real numbers R., Sol., (ii) False, e.g. between /2 and /3 there are infinitely many numbers, and these can not be represented in the form m, where m is a, natural number., (iii) False. All rational numbers are also real numbers., Q.2. Are the square roots of all positive integers irrational? If not, give an, example of the square root of a number that is a rational number., Sol. Square roots of positive integers are not irrational. For example, 4 = 2,, which is a rational number., Q.3. Show how 5 can be represented on the number line., Sol. To represent 5 on the number line we take a length of two units from, O on the number line in positive direction and one unit perpendicular to, it. The hypotenuse of the triangle thus formed is of length 5. Then with, the help of a divider a length equal to the hypotenuse of 5 units can be, cut on the number line., V5, 2, V5

Page 4 :
Page |1, 1, NUMBER SYSTEMS, EXERCISE 1.3, Q.1. Write the following in decimal form and say what kind of decimal, expansion each has :, 36, (i), 100, (ii), 11, 1, (iii) 4, (v), 11, 329, (vi), 400, (iv), 8., 13, Sol., (i) 0.36, terminating., (ii) 0.09, recurring non-terminating., (iii) 4.125, terminating., (iv) 0.230769, recurring non-terminating., (v) 0.18, non-terminating recurring., (vi) 0.8225, terminating., Q.2. You know that, = 0.142857. Can you predict what the decimal, 2 3 4 5 6, expansions of, are,, 7'7'7'7'7, without actually doing the long division?, If so, how?, 1, 4, 1, = 4x= = 0.571428, 7, 1, Sol., 7, 0.285714,, 3x, = 0.428571, = 2x- =, 7, 7, 7, 1, = 5x= = 0.714285, 7, 6., = 6x= = 0.857142, 7, 1, 7, 7, Q.3. Express the following in the form of, where, and, q are integers and, 9 # 0., (i) 0.6, (ii) 0.47, (iii) 0.001, Sol., (i) x = 0.6, = 0.666 ... to be written in, form., One digit 6 is repeating., We multiply it with 10 on both sides., 10x = 6.6, 10x = 6 + x, 10х — х 3 6, 9x = 6, 2, Ans., X =, 9.

Page 5 :
Page | 2, (ii) х %3, 0.47, = 0.4777, One digit is repeating., We multiply by 10 on both sides., 4.7, ..., 10х, = 4.3 + .47, = 4.3 + x, 9x = 4.3, 4.3, X =, 9., 43, Ans., 90, (iii) x = 0.001., Here three digits repeats; we multiply with 1000., 1000x = 1.001, 1000x, = 1 + x, > 1000x – x = 1, 999x =, 1, 1, Ans., x =, 999, Q.4. Express 0.99999, in the form 2. Are you surprised by your answer? With, your teacher and classmates discuss why the answer makes sense., 0.5, One digit repeat; we multiply by 10., 9.9, Sol. x = 0.99999 ..., %3D, 10x, → 10x = 9 + x, = 9x, 9., X =, 1 Ans., The answer makes sense as 0.9 is infinitely close to 1, i.e., we can make, the difference between 1 and 0.99, enough 9's., as small as we wish by taking, Q.5. What can the maximum number of digits be in the repeating block of digits, 1, ? Perform the division to check your, 17, in the decimal expansion of, answer., Sol. The maximum number of digits in the repeating block is 16 (< 17)., 1, = 0.0588235294117647, 17, Division gives, The repeating block has 16 digits. Ans.