Page 1 :
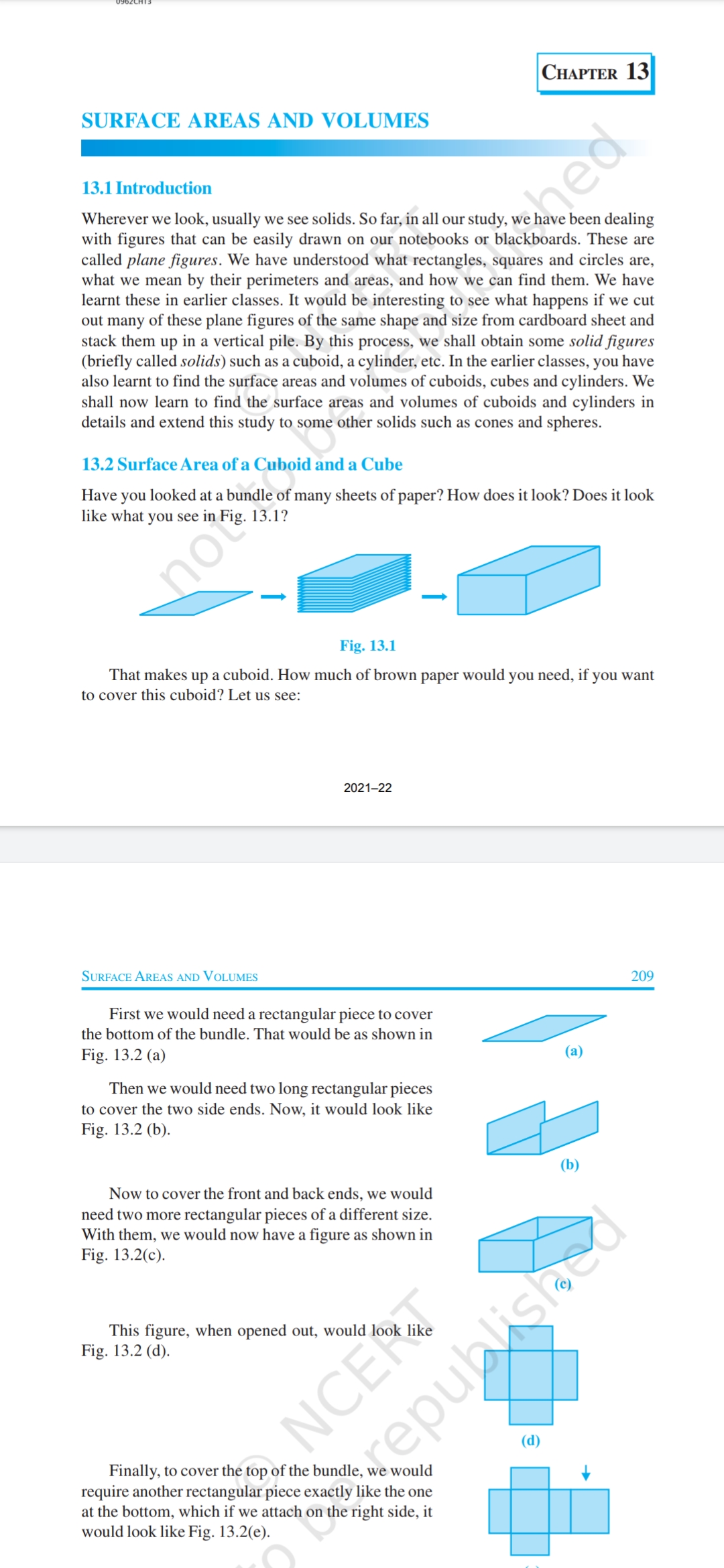
SURFACE AREAS AND VOLUMES, , 13.1 Introduction, , Wherever we look, usually we see solids. So far, in all our study, we have been dealing, with figures that can be easily drawn on our notebooks or blackboards. These are, called plane figures. We have understood what rectangles, squares and circles are,, what we mean by their perimeters and areas, and how we can find them. We have, learnt these in earlier classes. It would be interesting to see what happens if we cut, out many of these plane figures of the same shape and size from cardboard sheet and, stack them up in a vertical pile. By this process, we shall obtain some solid figures, (briefly called solids) such as a cuboid, a cylinder, etc. In the earlier classes, you have, also learnt to find the surface areas and volumes of cuboids, cubes and cylinders. We, shall now learn to find the surface areas and volumes of cuboids and cylinders in, details and extend this study to some other solids such as cones and spheres., , 13.2 Surface Area of a Cuboid and a Cube, , Have you looked at a bundle of many sheets of paper? How does it look? Does it look, like what you see in Fig. 13.1?, , Ss ee, , Fig. 13.1, , That makes up a cuboid. How much of brown paper would you need, if you want, to cover this cuboid? Let us see:, , 2021-22, , SurFace AREAS AND VOLUMES 209, , First we would need a rectangular piece to cover, the bottom of the bundle. That would be as shown in, Fig. 13.2 (a), , Then we would need two long rectangular pieces, to cover the two side ends. Now, it would look like, Fig. 13.2 (b)., , Now to cover the front and back ends, we would, need two more rectangular pieces of a different size., With them, we would now have a figure as shown in, Fig. 13.2(c)., , (a), (b), (©), This figure, when opened out, would look like, Fig. 13.2 (d)., (da), (on, , Finally, to cover the top of the bundle, we would, require another rectangular piece exactly like the one, at the bottom, which if we attach on the right side, it, would look like Fig. 13.2(e).