Page 1 :
UNIT-, , Chapter 1, , PROPERTIES OF MATTER, AND, , NON-DESTRUCTIVE TESTING, ELASTICITY, , Introduction:, We know that in case of solids, the distance between two, molecules i small and fixed. Solids have good amount of force of, attraction between their molecules. The molecules of solid are at fixed distance from each other and have strong force of, , attraction between them and the molecules behave as if they are connected with the help of springs. Thus if forces from all, sides are applied on a body then the body gets compressed and if these forces are removed then the body regains its size, and shape and becomes same as earlier., , MOLECULAR THEORY OF ELASTICITY (EXPLANATION OF ELASTICITY), , 1.1 ELASTICITY, 1., , Consider an elastic body as shown in Fig. 11 (a). Molecules are at equal distances from each other. There is a force of, attraction between the molecules. Hence, molecules are at equal distances:, , 2., , Refer Fig. 11 (b). Consider an external force applied on a body. Because of external force, every molecule starts, moving undesirely in the direction of force. They stop moving at a particular position where this applied force is, balanced due to equal and opposite force., , 3., , Refer Fig. 1.1 (c). Due to shifting of molecules, a body changes its size and shape and the body is said to be deformed., , Deforming force (Definition): The force applied on body which is responsible to deform (change size and shape ofthe, body) is called as deforrming force, , Deformation, , Deforming force, , Under deformed condition, every shifted molecule tries to achieve its original position due to which an intermal restoring, , force is developed inside a body., , Internal restoring force: Under deformed condition, everyshifted molecule tries to achieve itsoriginal position (because, ofelastic property). When a body is deformed because of external force, internal molecular forces are set up within the body, which, tend to oppose the changes in size and shape of the body., Internal restoring force (Definition) : The force which is responsible to restore original size and shape of the body is, , called as internal restoring force., Applied force = Internal restoring force, , 4, , Refer Fig. 1.1 (d). Now if extenal applied force is removed then because of intemal restoring force, body regains its, original size and shape i.e. Elasticity., , Body regains its original size and shape (exactly) on removal of external deforming force if and only if external force is within, a certain limit called as elastic limit. If external force is too large then the intramolecular structure of body collapses and there will, be permanent deformation (i.e. body does not regain its original size and shape on removal of extemal deforming force) and, , body looses its elasticity., (1.1)

Page 2 :
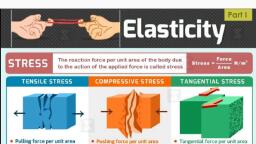
Applied Science : Physics (Mechanical), , Properties of Matter and Non-Destructlive Testing, , 1.2, , Applied force, (extermal, , Applied force, , defomin9, , (extemal, , force), , defoming, force), , (b), , (a), Original body, , Extemal force, is removed, , c), , Particles start, moving in, , Body is, , deformed, , the direction of, , applied force, , (no more, , original form), , (d), Body, , regains its, original, size and, , shape, , Fig.1.1, Elasticity, Plasticity and Rigidity:, ( ) Elasticity: When a force is applied on a body, size and shape of a body changes and the body is said to be deformed., Under deformed condition, the internal force is developed which tries to restore the original (position) size and shape of a body, called as internal restoring force. Because of this intemal restoring force developed inside a body, the body regains its original, size and shape on removal of external deforming force., Elasticity (Definition) : The property on account of which à body regains its original size and shape on removal of external, , defoming force is called as elosticity., The body which regains its original size and shape on removal of extemal deforming force is called as elastic body., eg. almost all metals- steel, brass, rubber, copper., , Some bodies which exactly regain their original dimensions on removal of external deforming forces are called perfectly, elastic bodies., , e.g. quartz, (2) Plasticity : Some bodies do not oppose the change in size and shape and thus deforms very easily. Such bodies do not, regain their original size and shape even after the deforming force is removed. These are called plastic bodies., eg. clay, putty, chalk., , Plasticity (Definition) : The property on account of which a body easily deforms and does not regain its original size and, shape on removal of external deforming force is called as plasticity. ie. material undergo permanent deformation., , (3) Rigidity: A body in which it is not possible to produce any relative displacement of the different particles inside it and, hence size and shape of a body remains unchanged even after large force is applied on it, is called as rigid body. No body is, perfectly rigid but stone is taken as a rigid body., Rigidity (Definition) : The property on account of which a body does not change its size and shape even when a large force B, applied on it, is called as rigidity., , 1.2 STRESS, STRAIN AND THEIR TYPES, When external force is applied on a body, by keeping its other end or face fixed, then molecules start moving in the direction, , of force. They stop moving at particular position where this applied force is balanced due to equal and opposite forces. Duet, shifting of molecules, body changes its size or shape and a body is said to be deformed. Under deformed condition, eve, shifted molecule tries to achieve its original position due to which an internal restoring force is developed inside a body. T, which is responsible to defom a body is called a deforming force. Thus, force, , Applied force (i.e. deforming foorce) = Internal restoring force, , (A) STRESS AND ITS TYP, 1.2Stress, (Definition): Stress is defined as internmal elastic restoring force per unit cross-sectional area ofa body., Stress, , ie., , But,, Thus stress, , Restoring force, can, , also be defined, , =, , Internal elastic restoring force, Cross-sectional area, , = Applied force, as, , applied force per unit cross-sectional area of a body.

Page 3 :
Applied Science: Physics (Mechanical), , Thus,, , or, , Stress =, , Internal restoring force, Applied force, Cross-sectional area, Cross-sectional area, , S.L. unit of stress is N/m or (Pa), , C.G.S. unit of stress is, The, , Properties of Matter and Non-Destructlve, , Cross-sectional, Applied forcearea, , Stress, , M.K.S., , 1.3, , Stress, , pascal., , dyne/cm?., , dimensions of stress, , are, , [L MhT), , Note Dimensions of stress and, pressure are same since Pressure Stress, Types of Stresses:, Types of stresses, , (1), , (2), , Tensile stress, , ), , Compressive stress, , or, , Longitudinal stress, , Shearing stress, , Or.., Volume stress, , or, , Shear stress, , or, , 1, , Tensile stress or, , Definition, , elongated, , When, , :, , Volumetric stress, , Longitudinal stress:, , body then, , longitudinal stress., , the, , applied force produces hange, , corresponding, , stress is, , called, , in, , length of a, , tensile stress or, , L, Original length, I, =, , OR, , Increase in length, , ., , Definition, , : The, , stress that tends to, , called longitudinal stress or tensile stress., Tensile stress = ", , change, , the, , length of a bodyis, , Applied force, , Cross-sectional area, Mg, T(where, r is radius of the wire), , M.K.S. unit of tensile stress is, N/m., C.G.S. unit of tensile stress is, The, , dimensions, , dyne/cm., , of tensile stress, , are, , [LM*T, , F Weight = mg, , force), Fig. 12, , amples: Rope climbing, bicycle chain, cables of lift elevator., , Compressivestress or Volumetric stress, ompressive stress (Definition): The stress which compresses the given body is called as compressive stress., , Testing

Page 4 :
APplied Sclence: Physics (Mechanical), , Properties of Matter and, , 14, , Non-Destructive Ta, , Extemal defoming, force, , Decrease, , (change), in volume 'dv, Original, , V-Original volume, , volume, , Decrease (change) in volume, (V- dv)- New volume, , dv, , Metal tube, , Three-dimensional, view, , Fig. 1.3, Volume stress (Volumetric stress) (Definition): If a deforming force produces change in the volume of a body, then the, , Corresponding stress is called as volume stress., OR, , Definition: The stress which changes volume of a body is called as volume stress., Volume stress=, , force, Applied, Area, , Change, , in, , pressure o, , M.K.S. unit of volume stress is N/m., C.GS. unit of volume stress is, dyne/cm ., Dimensions of volume stress are, , [LMT*, , Examples: Piston, shock absorbers etc. Concrete is very strongin compression but it is weak while pulling., 3. Shear stress:, Consider a metal block ABCDEFGH of which, , the base DCGH is fixed. A tangential force 'F is, applied to the top surface as shown., The block gets twisted (it changes its shape), and when equilibrium is reached, it takes the, shape of parallelopiped DCGHA'B'FE., , A', , Tangential, F, force, , B, , B, , B, , 8, , Here volume of a body remains the same,, shape of a body changes a little. Hence angle e by, which it is twisted is very small., , Fixed surface, D, , C, , Front view, Fig. 1.4, , Shear stress:, Definition : The stress corresponding to change in shape of a body is called shear stress., OR, , Definition : f deforming force changes shape of a body, then the corresponding stress is called shear stress., OR, , Definition: The tangential force per unit area ofthe surfoce is called shearing stress., Shear stress, , Tangential force, , Tangential force 'F, , Area of surface, , Area of surface AEDH, , VC, , M.K.S. unit of shear stress is N/mn., , c6S. unit of shear stress is dyne/cm, Dimensions of shear stress are [L MTI, Examples: Torsional pendulum, metal sheet cutter, shaft connecting fiy wheel, bone fracture because of bending., , 12 (B) STRAIN AND ITS TYPES, We have seen that when a force is applied on a body keeping its one of the end fixed then either size of the body chang, or its shape changes ie. its dimensions change., , or

Page 5 :
Applied Science: Physics, (Mechanical), Strain, , (Definition): The change in dimensions per, , Definition: The strain is the amount, Definition: Strain is the ratio of, Strain, , 1.5, , of Matter and, unit original dimension Properties, Non-Destructive Testing, is called, , of change in size (or, , change in dimensions to, , Change in dimension, , Since strain is the ratio of, Original, two similar, Strain is a, , strain., , OR, , shape) of material per unit, , OR, the original, , dimension of the material, , dimension, quantities, it has no unit., , pure number., , Types of Strains:, , original size (or shape) of it., , Types of strains, , (1), , Tensile strain, , (2), , Volume strain, , Longitudinal strain, , (3), , Shear strain, , or, , Volumetric strain, , o, , Linear strain, , or, , or, , Compressive strain, Longitudinal strain or Linear strain:, If the, applied (defoming) force, then the corresponding strain is the produces change in the length of body, tensile strain., Definition: Tensile strain, (longitudinal strain) is defined as change in, per unit original length., length, , 1, , Shearing strain, , Tensile strain or, , a, , I, , L= Original, length, Increase in length, , OR, , Definition, , change, , in, , length, , Tensile strain, to the, , (longitudinal, , original length., , strain), , is, , defned as, , the ratio, , of, , L, , Tensile strain Change increase) in length, Original length, , Tensile strain New length-Original length, Original length, , Tensile strain =, It has no, , unit., , Volume strain, , M, , When, , applied force produces change, strain is the volume strain., , in volume then the, , Votume strain (Definition) : Volume strain, volume per unit original volume of a body., , is, , defined, , as, , coresponding, the, , change, , in, , Fig. 1.5, Force, , OR, , Definition: Volume strain is defined as the ratio of change in volume to the, a, body., Change in volume, Volume strain, , original volume of, , Original volume, , Volume strain, t, , has no unit., , dv, , Front view, V- Original volume, dv- Decrease, , (change) in volume, , Fig. 16

Page 6 :
Applied Science: Physics (Mechanical), , Properties of Matter and Non-Destructive Te, , (estng, , 1.6, , Tangential, , 3. Shearing strain, , A, , force A, , B, , F, , the, , applied force produces change in shape of a body (body gets, then the corresponding strain, produced is the shearing strain. As, a, shown in Fig. 1.7 the cube is converted into, parallelopiped., , We have,, , Original, volume, , Tensile:, , When spiral spring is stretched then the metal wire is twisted, Example:does, i.e. sheared, , (it, , Shearing, , not, , strain, , Applled Scie=, , Tensile=, , elongate)., , (Definition) : Shearing strain is defined as, layer to its distance from the fixed layer., , the ratio, , lateral displacement of any, , Shearing, , Fig. 1.7, , of, , A, , Lateral displacement of any layer, Its distance from the fixed layer, , train, , Lateral displacement of upper layer, , Shearing strain, , Its distance from the fixed, , where,, , layer, , AA', Shearing strain = AD, D, , D, , Fig. 1.8, , Shearing strain = tan, But, , even a, , large tangential force, , Ife is very small then, , is, , applied, , mathematically tan, , on a, =, , metal cube it gets twisted with, , a, , little amount i.e. 0 is very smal", , ., , CGS un, Dimens, , Shearing strain = Shear = e (in radian), , INote:, , 1.2.1 Elastic Limit and Hooke's Law, Elastic limit (Definition): "The stress, corresponding to the limiting value of the load, which when, released, does not, ,',., permanent deformation is called as elastic limit"., , produce, , If this limit is, , crossed,, , the, , proportionality, , Its S.C, , is lost and the stress is found to be less than what is, , structure of body collapses., , applied and subsequenty, , expected, , and, , Bulk M, Definit, , Bulk mc, , intramolecular, , Hooke's law (Statement) : It states that, "within elastic limit, strain is directly proportional to the stress.", Strain, , Stress, , Strain, , Stress, , OR, , Strain, , Constantx Stress, Constant, , The constant of proportionality is called as modulus of elasticity., , Stress, , Modulus of elasticity, S.I. unit of modulus of elasticity is, , Strain, , N/m2, , CGS unit is dyne/cm2, Dimensions of modulus of elasticity, , are, , [L-1 M, , Its S.Lo, , T-2], , CGS uni, , 1.2.2 Types of Moduli of Elasticity, As we have seen when a force is applied on a body, then its, Accordingly, there are three types of modulus of elasticity., , Its dime, length changes or volume changes or shape of a body change, , Compre, Compressibil, Definiti-, , 1, , Young's Modulus of Elasticity ():, Definition: Within elastic limit, the ratio of tensile stress to tensile strain is called Young's modulus of elasticity 'Y., , Young's modulus of elasticity measures the opposition (resistance) offered by material for its change in length.

Page 7 :
Applied Science:Physics(Mechanical), , Propertiess of Matter and Non-Destructive Testing, , 1.7, , We have,, , Stress=, Strain, , Constant, , Modulus, , =, , of elasticity, , I, , L = Original, length, Increase in length, , Tensile stress= Young's modulus of elasticity = Y, Tensile strain, , Y, , Tensile stressF/A, Tensile strain, Mg/r2, , L, , MgL, , tr1, , M = Load attached, , where,, , Radius, L, , I, , of wire, , Original length, , of wire, , = Extension produced, , M, Fig. 1.9, , Tts S.I. or MKS unit is N/m2, CGS unit is dyne/cm2., Dimensions are [L--M'T). Dimensions of Y are same as stress., Note: Dimensions of stress and all moduli of elasticities (ie. Y, K, n) are same.], , 2 . Bulk Modulus of Elasticity (K):, Definition: Within elastic limit, the ratio ofvolume stress to volume strain is called bulk modulus of elasticity '*., , Bulkmodulus measures the opposition(resistance)offered by a material during its change in volume., Bulk modulus ofelasticity, , Area, , Force F, , K, , Volume stress, , K, , dvN, , Volume strain, , Bulk stress, Bulk strain, , F/A, , dp, K dv/N, , dv, , K, , K, , QpXV, , dv, , where,, , V, , V original volume, , Front view, , F, , Fig. 1.10, , applied force, , dv = decrease in volume, , dp= increase in pressure, A, ts S.L or MKS unit is, CGS unit is, , area of cross section on which force is applied, , N/m2., , dyne/cm., lts dimensions are [L-1 M'T-2. Dimensions of K are same as stress, Y etc., , Compressibility: The property, , on, , account, , compressibility ie. it is the ability to compress, , of which, , a, , body can be compressed by the opplicotion, , Definition: 7he reciprocal of bulk modulus of elasticity is called compressibility., , Compressibility= Bulk modulus, , dp, , dv, , dp V, , ofexternol force is calledas

Page 8 :
Applied Science: Physics, (Mechanicay., Bulk modulus meast, asures the opposition, permission given by, , the, , Properties of Matter and Non-DestructiveT., , 1.8, , made by the material to change its volume and compressibility mea, , measures, , material for its compression., , Compressibility represents strain per unit stress., Volume strain, , Compressibility, , Volume stress, , The S.I. unit of, compressibility is m'/N., The C.G.S. unit of, compressibility is cm'/dyne., 3., , Dimensions of compressibility are [L' M, , TI. Dimensions of compressibility are exactly inverse of K., , Modulus of Rigidity (n):, Definition : Within elastic limit,, , of shearing, , the ratio, , stress to, , shearing strain, , is called modutus, , of rigidity 7., , Modulus of elasticity measures the opposition (resistance) offered by a material for its change in shape., BBModulusof rigidity,, Tangential, Tangential, , force, , Shearing stress, , force, , Shearing, Lateral, , Fixed surface, D, , Area, , F, , =, , A, , or, , AA/AD, FIA, , which, , tan 6, , force is applied, , |, Its S.L, , F/A, , .n, , tangential force, area on, , MKS unit is, , A, , CGS unit is dyne/cm2., , For, , a, , given material, there, , of n are same as stress, Y, K etc., , is certain relation betwe, , Y, , 3K +, , where,, , Y, , or, =, , K, , Y, K and n which is given by,, , 3n9k, , Young's modulus of, Bulk modulus, , elasticity of material, , Modulus ofrigidity, 3 STRESS-STRAIN DIAGRAM OR BEHAVIOUR OF A, METAL, WIRE UNDER CONTINUOUSLY INCREASING LOAD, Breaking stress, , OB, Stress, , ----Strain'Set, , Fig. 1.12, , E Elastic limit, Yield point, B Breaking point, S Set point, D Ultimate stress, , Y, , =, , A, AOtant, If 'e' is, , tan |, , Ae, , N/m2., , Dimensions are [L-1 MT-2] i.e. Dimensions, Relation between Y., K and n:, , F/A, , displacement of layer, , LIts distance from fixed layer, , Front view, , Fig. 1.11, , where,, , strain, , small, , put tan 09=

Page 9 :
Applied Science:Physics (Mechanical), A wire is, , subjected, , to, , increasing, , load, , Properties of Matter and Non-Destructive Testing, , 1.9, step by step. A graph of, , stress, , against strain is, , as, , shown. It, , can, , as, , be explained, , follows., OE portion is a straight line which indicates that stress is proportional to strain i.e. wire obeys Hooke's law upto, point E., , The stress corresponding to point E is maximum stress to which wire can be loaded without any permanent elongation., , This is called elastic limit of wire., , EE portion is curved towards strain axis which shows that increase in strain is more than what is warrantied (expected), by corresponding increase in stress i.e. strain is not proportional to stress i.e. Hooke's law is not obeyed., At any point between E and E' if all the load is removed, then some permanent elongation occurs in the wire, this is, called set., , When wire is again subjected to a load, a new straight line SE' (shown by dotted line) is obtained indicating Hooke's, , law., Some portion after point Y is almost parallel to strain axis i.e. strain increases without increase in stress just like wire, , fiows, this is called yielding. This is called plastic flow. The point at which this flow begins is called yield point Y. The, , value of stress corresponding to yield point is called yield stress., With the plastic flow, wire becomes thin and thin. Some weak points called neck are formed in the wire. The wire, becomes thin and thin in the region of neck, where the strain increases speedily and stress decreases and ultimately at, , weakest point wire breaks the corresponding point 'B' in the graph is the breaking point., Brittle materials like high carbon steel etc. break immediately after elastic limit is crossed. Ductile materials like copper,, , wrought iron undergo plastic deformation and its length goes on increasing then wire breaks., , Breaking stress: The maximum stress upto which wire can be loaded or wire can bear s called breaoking stress. The, , Corresponding point in the graph, , is the, , Breaking stress (Definition): t, , breaking point B., , is the maximum stress at which the wire brakes., , Ultimate stress (Definition): t is the maximum stress the system is copable ofwithstanding., , Ultimate stress (Definition): Uitimate stress is defined os the ratio ofmaximum load thoat the specimen (system) is capable of, , withstanding to its original cross-sectional area., Ultimate stress, , Maximum load the system can withstand, Original cross-sectional area, , Working stress (Definition), , :, , It is the actual practical stress, , on, , the system., , Working stress (Definition) : working stress s defined as the ratio of actuat load to the originat cros-sectionat area, Working stress =, , Actual load on the specimen (system), Original cross-sectional area, , Factor of safety : Working stress is the maximum allowed (permitted) stress on the system. For the safety of structure, this, , working, , stress should be less than elastic limit of the material., , Working, , stress is determined, , by dividing, , the ultimate stress, , by, , a, , number called factor of safety., Factor of safety (Definition): Factor ofsafety is definedas the ratio of ultimate stress to working stress, , Factor of, , safety, , Ultimate stress (load), , working stress, , (loaa), OR, , ractor of safety is also defined as the ratio of maximum load that the structure can bear to the actual load on the structure., , ror example, the weighing balance used in grossary shop. Even though the weigh balance can bear a load of 10 kg, the, , message written on it may be "only for 5 kg"., dmple Message on lift may be only for 5 persons but actual capacity may be of 20 persons.

Page 10 :
AppliedScience:Physics (Mechanical), , Properties of Matter and Non-Destructive Testing, , 1.9, , A wire is subjected to increasing load step by step. A graph of stress against strain is as shown. It can be explained as, , follows., OE portion is a straight line which indicates that stress is proportional to strain i.e. wire obeys Hooke's law upto, , point E, corresponding to point, This is called elastic limit of wire, , The stress, , EE portion, , E is, , maximum stress, , to, , which wire, , can, , be loaded without any, , permanent elongation., , is curved towards strain axis which shows, that increase in strain is, , more than what is warrantied (expected), by corresponding increase in stress i.e. strain is not proportional to stress i.e. Hooke's law is not obeyed., , At any point between E and E' if all the load is removed, then some permanent elongation occurs in the wire, this is, called set., , When wire is again subjected to a load, a new straight line SE' (shown by dotted line) is obtained indicating Hooke's, , law., , Some portion after point Y is almost parallel to strain axis i.e. strain increases without increase in stress just like wire, flows, this is called yielding. This is called plastic flow. The point at which this flow begins is called yield paoint Y. The, value of stress, , corresponding to yield point is called yield stress., , With the plastic flow, wire becomes thin and thin. Some weak points called neck are formed in the wire. The wire, , becomes thin and thin in the region of neck, where the strain increases speedily and stress decreases and ultimately at, weakest, , point wire breaks the corresponding point, , '8, , in the, , graph is the breaking, , point, , Brittle materials like high carbon steel etc. break immediately after elastic limit is crossed. Ductile materials like copper, wrought iron undergo plastic deformation and its length goes on increasing then wire breaks., , Breaking stress: The maximum stress upto which wire can be loaded or wire can bear is called breaking stress. The, , corresponding point in the graph is the breaking point B., Breaking stress (Definition): t is the maximum stress at which the wire brakes., , Utimate stress (Definition): /t is the maximum stress the system is capable ofwithstanding., , Utimate stress (Definition): Utimate stress is defned as the ratio ofmaximum load that the specimen (system) is capable of, , withstanding to its original cross-sectional area., Ultimate stress, , Ioadthesystem can withstand, , =, , Original cross-sectional area, , Working stress (Definition): t is the actual practical stress on the system., , Working stress (Definition): Working stress is defined as the ratio of actual load to the original cross-sectional area., Working stress =, , Actual load on the specimen (system), Original cross-sectional area, , Factor of safety : Working stress is the maximum allowed (pemittecd) stress on the system. For the safety of structure, this, stress should be less than elastic limit of the material. Working stress is determined by dividing the ultimate stress by a, , working, , number called factor of safety., Factor of safety (Definition): Foctorofsafety is defined as the ratio of ultimote stress to working stress, Factor, , of safety, , Ultimate stress (load), , Working stress, , (loaa), OR, , ractor of safety is also defined as the ratio of maximum load that the structure can bear to the actual load on the structure., , O example, the weighing balance used in grossary shop. Even though the weigh balance can bear a load of 10 kg, the, , message written on it may be "only for 5 kg"., ample: Message on lift may be only for 5 persons but actual capacity may be of 20 persons.

Page 11 :
Properties, , 1.10, , Applied Sclence : Physics (Mechanical), , of Matter and Non-Destructive, , 1.3.1 Poisson's Ratio, When metal wire is stretched, its, becomes thinner., Strain is the ratio of, , in dimensions to, , change, , original dimension., , length increases butit, , its, , If one end ofthe metal wire is fixed to the rigid support, and load is attached to its free end, then change in, dimensions takes place by two ways, Along the direction of force: Along the length, , ofwire ie. longitudinal ie. tensile, , L, , length of the, , wire increases i.e. longitudinal extension., , 2. In the perpendicular direction of force: Along, the sides ofthe wire i.e. lateral i.e. transverse diameter of, , the wire decreases i.e. lateral contraction., , Thus it has two types ofstrains: longitudinal strain and, lateral strain., , Longitudinal strain (Definition) : t is the ratio of, increase in length to the original length of the wire., , M, Fig., L, , Let, , 1.13: Diagram showing increase in, decrease in diameteer, , length and, , Original length ofthe wire, , Increase in length of the wire (extension), , Increasein length, , Longitudinalstrain, , Original length, , Lateral strain (Definition): It is the ratio of decrease in diameter to the original diameter ofthe wire. Let, D Original diameter of the wire, , dDecreasein diameter., , Lateral strain, , Decrease in diameter _d, Original diameter, , Poisson's ratio: As length of the wire goes on increasing, the wire becomes thinner and thinner, i.e., , Lateral strain, , Longitudinalstrain., , Thus for a given material within elastic limit, the lateral strain is directly proportional to the longitudinal strain., Lateral strain o Longitudinal strain, , Lateral strain, , Constant x Longitudinal strain, , Lateral strain = ox Longitudinal strain, , Lateral strain, Longitudinal strain, , o, , Constant = (Poisson's ratio), , Poisson's ratio () (Definition): Poisson's ratio is defined as the ratio oflateral strain to the longitudinal strain., For a given material, within elastic imit this ratio is constant., , Poisson's, , ratio, , CoR, , mo, , Lateral strain, , Longitudinal strain, - d/D, L, , Poisson's ratio has no unit and no dimension. o can be positive as well as negative. The maximum positive value ofo, and minimum negative value of o is-1., , resto, (stret

Page 12 :
Applied Science:Physics (Mechanical), , 1.11, , Properties of Matter and Non-Destructive Testing, , 1.3.2 Factors Affecting Elasticity, , We have seen that elasticity is materal dependent i.e. for, a given material,, elasticity is constant. The structure of, its elastic, Metals are an, of large number of, aggregation, crystallites which are arranged in random, is, Even though, for a given, material, following are the factors which affect elasticity i.e. for a given, material, following factors affect elasticity., , greatly affects, , materia, , properties., elasticity constant, , fashion., , 1. Effect of temperature:, , majority, , as, , the, , cases,, temperature of material increases, the, elasticity of material decreases and vice a versa. As the, the, material increases, the distance, of, temperature, between the molecules increases and hence, intramolecular force decreases, which result in decrease in internal restoring force and hence, elasticity decreases., If lead is cooled in liquid air, it becomes elastic., , In, , carbon filament is elastic at ordinary, temperature but it, But invar steel is exception for this. In case of, invar, expansion, the elasticity remains unaffected, A, , Effect, , 2., , by change of temperature., , ofannealing:, , In the process of, material decreases., Due to, , annealing, the, , annealing, , large crystal grains, , becomes plastic when heated by passing current, through it., steel, nickel 36%, iron 64%, alloy low coefficient of thermal, , metal is heated and then cooled, , gradually., , Because of, , annealing,, , the, , elasticity, , of the, , the smaller, , takes, , elasticity., , crystals present inside the material get oriented in one, particular direction and formation of, place: Thus softening of the materials takes, place, which increases the plasticity and decreases the, , 3. Effect of hammering and rolling the material, The metals with smaller grains are, stronger than those with, crystal grains break up into smaller units which increases, , increase the elasticity and decrease the plasticity., Effect of impurities:, The, , impurity affects, , larger grains. Due to operations like hammering and rolling, the, properties of the material. Thus hammering and rolling, , elastic, , '', , the, , elastic. properties, , of the material to which, , Sometimes suitable impurities are, theywithout disturbing, deliberately added to metals to increase bindings between the crystal grains, their orientation. The elastic, properties are strengthened by adding impurities to the metal., e.g. To strengthen elastic properties: To strengthen elastic, few amount of carbon in molten steel are added., In some cases, , by addition, , of, , impurity, , in the, , properties,, , are, , added., , few amount of, , potassium, , in, , gold, , are, , added and, , material, the elasticity decreases., , Effect of recurring stress:, If, , repeated, , stress is, , applied, , on, , the, , same, , decreases the elasticity., , body then softening, , of material takes, , Which is more elastic steel or rubber ?Why ?, Steel is more elastic than rubber:, If a body resists deformation, , Ans., , and, , place, , recovers, , immediately on removal of external deforming force then it is called perfectly elastic body., , We have,, , and increases the, , (regains), , its, , plasticity and, , original, , size and, , hence, , shape, , /L, Y, where, Y = Young's modulus of elasticity. F = Restoring force,, , n, , I, , =, , Extension, , produced, , in the wire, , case of elastic bodies, a force of opposition starts building while deforming the body. If steel and rubber are taken under, , Consideration, steel offers more opposition to produce change in shape and size. Hence steel is more elastic., in case of steel, restoring force is more and extension produced is less (approximately 2% of original length) ie. elasticity is, , more., Yfor steel = 2x 101l N/m2, On the other hand, in case of rubber, rubber offers less opposition to produce change in size and shape. In case of rubber,, i n g force is less and extension is more (may length get doubled) i.e. elasticity is less. Y for rubber, , 1.25 x 107N/m2., , Note: If rubber is stretched even ten times its original length and released then it regains its original length. In this regard, , stretching), rubber is more elastic.

Page 13 :
Applied Sclence: Physics, (Mechanical)., mportant Points, , Properties of Matter and Non-Destructivet, , 1.12, , Appl, , icity s defined as the property by virtue of which body regains its original size and shape on removal of e, , Xtetm, , deforming force., Factors, , stress., , affecting elasticity are: (1) temperature, (2) annealing, (3) hammering, , and, , rolling, (4) impurty, , and, , (5), , Whic, , Stress is defined as internal resistive (restoring) force developed per unit cross-sectional area., , Strain is defined as ratio of change in dimensions to, Hooke's law states that, within elastic limit, stress is, , (longitudinal) stress, Young's modulus, Y Tensile, Tensile, , recui, , original dimensions., directly proportional to strain., , (longitudinal) strain, , Compressibility, Bulk, , stress, modulus, K Volume, Volume strain, =, , Modulus, , of, , stress, rigidity, Tn Shearing, Shearing strain, , Factor of safety is defined as the ratio of, maximum load that the structure can bear to the actual load, It should always be, greater than one., Breaking stress : It is the maximum stress at which wire brakes., Utimate stress : It is the maximum stress the, system is capable of withstanding., Working stress : It is the actual, stress on the, , Poisson's ratio: It is defined, , practical, , as, , 1., , Stress =, , 2., , Longitudinal strain =, , F, , Volume strain =, , =, , e, , (if e, , L, , is, , small), , dv, , WE, , Area, -, , tan 0, , (a, , Force in newton 'N', , A, , =, , structureelong, , of lateral strain to the longitudinal strain., , where,, , Shearing strain, , the, , system., , the ratio, , Formulae, , Ex, on, , -, , Increasein length, Original length, , Decrease in volume, , V - Original volume, M, , 4., , K, , Load in kg, , -, , Radius of wire, , P, , Pressure applied, , Thus, , FV, , A(dv), , dv, , 5., , Compressibility =, , 6., , n, , 7., , Y=K, , Exa, , following, (a), , E, , Atan, , Y, , Ae, , K, , 3K+, , Young's modulus of elasticity, Bulk modulus, , Modulus, 3., , Poisson's ratio, , dxL, G Dxl, , a, , =, , d/D, , /L, , d, , D, , ofelasticity, , (C), , Soluti, , of rigidity, , Decrease in diameter, , Original diameter, , = Poisson's ratio, , Hig

Page 14 :
Applied Science:Physics(Mechanical), , Properties of Matter and Non-Destructive Testing, , 1.13, , SOLVED EXAMPLES, Example 1: Four wires of same metal and same diameter are stretched by same load. Length of each wire is given below., , Which ofthem will elongate most?, (a) L = 0.5 m,, , (b) L = 1 m,, , (), , L = 1.5 m,, , (d) L = 2m., , Y is same., Four wires of same metal, Same diameter, Same load Fis same., Now only original length L' and elongation 't are variable, (changing)., , Solution:, , A is same., , We have,, , oLL= 2 m is maximum, , elongation in case of L = 2 m is most., , Ans.d)L= 2m, Example, , 2: Four wires, , elongate most?, , of same metal, , are, , stretched by, , same, , load. The dimensions, , are, , (a)r = 0.5 mm, L = 50 cm; (b) r=lmm, L = 100 cm; (c) r = 1.5 mm, L = 150 cm; (d)r = 2, , Solution:, , Y is, , same, , in all, , cases, , (since same metal). M is same, , given, , below. Which of them will, , mm, L = 200 cm., , Fis same., , Here r, Land l are variables., , We have,, , Y, , 50, , (a), , (0.05)?, , (b), , 0.1F10,000, , 20,000, , (herer0.5 mm = 0.05 cm), , 100, , 150, 0.15)?6666.67, , 200, 2, , (d), , 5,000, , Thus elongation in the first case will be the most, , Ans. (a), , Bxample 3: Four wires of different metals are stretched by different load. The dimensions are given below. Which ofthe, , following has highest "Y elasticity?, (a), , M, , 1 kg, r = 1 mm, ! = 1 mm, L= 1 mn, , C, , M= 3, , kg,, , r, , 3 mm, l, , =, , =, , Solution: We have relation,, In the case of, , Highest, , Ywill, , (a), , 3 mm, L, , =, , (d), , 3m, , M, Y-11, , be in the first case., , (b) M, , Ans. (a)], , 2 kg, r = 2 mm, l = 2 mm, L = 2 m, , M = 4 kg, r = 4 mm, l = 4 mm, L = 4m, , Y, 6) Y, , -05, , d) Y, , 025

Page 15 :
APplied Sclence : Physics (Mechanical)., , Properties of Matter and Non-Destructive T, , 1.14, , Nesinm, , p l e 4: The extension produced in a wire due to load is 2.mm. The extension in a wire of same material and length, nai the radius by the same load will be, bu, (a) 4 mm, (b) 6 mm, () 8 mm, (d)1 mm., , Solution : We have,, , Y, , g,, , Ttr, , Relation between l and r is, Now radius is half the earlier., , 1, , (1/2), , 4, , wire, , i.e, l is 4, , times earlier, , =8 mm Ans. (c) 8 mm, , Example 5:f T is the extension produced in the wire of length L, radius, of same metal of length 3 L radius 3r and a force 3F., Solution:, , Y, , Solution :, , force F, find, , a, , the extension, , produced in t, , .. (1), , 3Fx 3L, (3r, , =, Example, , with, , I, , Now,, , ifY = 2 x10, , r, , 6, , :, , A wire, , N/m?2, , Given:, , L, , of length, =3 m,, , l, , =1 Ans. Extension produced will be lsarme as 'earlier., , 3, , 3, , extends by 3, , mm, , =3x 103 m,, , =2N, , m, , mm, , F, , when, , a, , force, , is, , applied, , to it., , Calculate stress, , produced in, , Stress, Y Strain, Stress, , Yx Strain = Yx (/L) = 2x 1011 x, , Stress=2x 10"N/m], Example 7:A wire of diameter 3, modulus of material of wire, Solution : Given:, , mm and length 4m extends by 2.5 mm, , a, , force, , of 10 N, , is, , applied. Find the Young, , dia= 3 mm, r, , 1.5 mm = 1.5 x 10-3 m, , L =, , 4 mm, , I= 2.5, , We have,, , when, , mm, , F, , =, , 10N, , Y, , =, , ?, , Y, , A, , /L, , =, , 2.5 x 10-3 m, , (10)(4), FL FL, A)I (ar) (3.142) (1.5 x 10-3 (2.5 x10-3), , Y 2.26x10°N/m2, Example 8: Calculate Young's modulus of, for a wire, The wire elongates by2 mm when subjected to a load of 10 N., , elasticity, , Solution :Given: Y = ?, L = 100 cm, , We have, , Y, , 1 m, A = 1.96 x 10, , having length, , cm, , and cross-sectional, , m, l = 2 mm = 2x 10 m, F = 10 N., , FL, (10x 1), A (1.96 x 10s x (2 x 10*)), , Y=2.54 x10 N/m, , 100, , area, , 1.96, , x10

Page 16 :
Applied Science : Physics (Mechanical), , 1.15, , Properties of Matterand Non-Destructive Testing, , Example 9:A metal bar has a maximum stress of 6 x 10 N/m?. If the area of cross-section of the bar is 0.04 m, find the, maximum force that the bar can withstand., , Solution: Given: Maximum stress =6x 10° N/m, Area =0.04 m,, Maximum stress = Maximum force_, We have,, , Maximum force, , =, , ?, , Area of cross-section, , Maximum stress x Area, Maximum force, , = Maximum force, =, , Maximum stress x Area, , Maximum force =24 x10 N, Example, , 10: A, , copper, , wire is, , copper 1.2 x101 N/m, , Solution: Given: Since wire, , is, , stretched by 5%, , stretched 5%, take, , l, , =, , 6x 10°x 0.04, , of its length., =, , 5 and L, , Determine the stress, , produced, , in the wire. Given Y, , for, , 100, Stress =?, , Stress, , Y, , Strain, , Stress, , Yx Strain, , =, , Yx, , x10" x100), , Stress6x 10 N/m, Example 11:, , A, , longitudinal stress of 8 x 10 N/m2 produces an extension of 1 mm in a, , modulus of the material of the wire., Solution: Given: Stress, , =, , 8, Y, , x10 N/m2, I 1 mm 1x 10-3 m, L 2 m, Y, Stress Stress xL 8x10'x2, = Stress, =, , =, , Strain, , =, , wire, , of length 2, , metres. Fnd, , Young's, , ?, , 1x 103, , Y16x10 N/m], Example 12: Equal weights are attached to two wires of same metal, other. Calculate ratio of their extensions., Solution:Given: 1St wire, , The, , length and radius of one wire is 1.5 times that of the, , 2nd wire, , L 1.5L2, , Let length = l2, , 1.5, , Let radius = 2, , r2, ?, , YMg4, , (1), , Equating (1) and (2),, , 15L)2, , L(1.5r, , ie. Ratio of, longations of two wiresis 1:1.5, , Y, , Mgl, , . (2)

Page 17 :
Applied Sclence: Physics, (Mechanical), , Properties of Matter and Non-Destructive T, , 1.16, , estin, , n p e 13 : When a metal cube is subjected to a stress of 9 x 10° N/m, each side of the cube gets shortened by 1g%, volume strain and bulk, modulus of metal, , Solution :, , Let, , original (length) side of the cube l, Orniginal volume = 100 x 100 x 100, , Find Applied Scilen, , 100 units., , =, , Example, , is 1.5 mm. Calc, Solution:, , V 1000000 unit, But now, , due, , to, , applied, , stress, its side gets shortened by 1% i.e. becomes 99 units each., New volume = 99x 99 x 99 = 970299 unit, , We have,, , Change in volume = 1000000 -970299, , dv 29701 unit, Volume strain = dv, , 29701, , 1000000, , 0.0297, , Volume strain =0.03, Bulk modulus= Volume stress 9x10, , yolume strain, Bulk modulus K =3x10 N/m?, Example 14:A lead block of volume 1 m, Also calculate, , 0.03, , Practice Qum, , is, , subjected to a pressure of 10 N/m. Calculate the change, compressibility of lead. (Given: Bulk modulus of lead K 5 x10°, Solution: Given: V=1m, dp 10° N/m?, dv = ?, Compressibility ?N/m, =, , in volume of lead, , block, , 1., , Defi, , 2., , State-, , =, , =, , We have,, , =Opx, dv, , Bulk modulus, K, , dpxV_10 x1, K (5 x 100, , dv, , =, , Compressibility =0.2 x100 m'/N, Example 15 : 6 cm thick aluminium square plate has area 2.5 m. The lower, surface of plate is fixed and a, applied to the top surface and the top surface displaces by 0.08 mm. Calculate, tangential force, shearing, stress, shearing strain., (Given: Modulus of rigidity of aluminium n 3 x100 N/m), =, , 0.06 m, , Shearing strain =, , cm, , =, , 0.06 m,, , AA, , =, , 0.08, , mm, , =, , Lateral displacement of any layer, Its distance from fixed, , layer, , 0.08, , AA, AD, , x, , 10, , Defin, , 9., , State, , 10., , Defin, , 11., , Defin, , 12., , Defin, , 13., , Distire, , 14., , Defin-, , 16., , Statee, , 17., , State, State, , Define, , 21., , Correc, , Shearing strain, , Shearing stress=3.99x10'N/m, , 0.06, , 22., , Define, , 3. T.E. Quest., ., , Out o, , 3., , DefineDefine, Define, State a, , Explain, , Shearing strain, , nx, , Expla, , 8., , 19., , m, , 0.08 x10, , Shearing strain =1.33 x103, Modulus of rigidity, T= Shearing stress, Shearing stress, , Expla:, , 20., , Side view, , Fig. 1.14, 6, , Defin, , 18. Defin, D, , =, , 5., , 15. Expla, , 0.08 x 10, m, , AD, , Expla, , 7., , Compressibility (5x 105, , Solution:Given:, , Defin, , 4., , 6, , dv= 2x105m, , =, , 3., , =, , (3, , x, , 10) x (1.33 x 103), , 4., 5., , 6

Page 18 :
Applied Science:Physics (Mechanical), 1.17, Example 16:A metal wire of length 2 m and, ic1.5 mm. Calculate lateral contraction of the, diameter 0.7, wire., Solution: Given:L=, , We have,, , 2 m, D =0.7, mm, , =, , 0.7, , x, , Lateral strain, , Poisson's ratio, a =, , mm, , (Given: Poisson's ratio,, , 10, , m, l= 1.5 mm, , is, a, , =, , Propertles of Matter and Non-Destructive Testing, stretched by a certain load and extension, produced, 0.25)., , =1.5 x 103m, d, , ?,, , g, , =, , 0.25, , Longitudinal strain, d/D, Dx, , xDx, , d, , L, , d -DxI_0.25x 0.7 x103 x15x103, , d 1.3x 10 m, , Practice Questions, 1., 2., , 3., , Define the terms : (0), Elasticity, (Gi) Stress, (ii) Strain, (iv) Elastic, limit, () Yield, State and explain Hooke's law., Define elastic body and, plastic, , point, (vi) Breaking point, , body and give one, , 8., , example of each., Explain:) Young's modulus, (i) Bulk, (ii), Modulus of, Define compressibility and state its modulus,, rigidity., S.I unit., Explain: ) Longitudinal (Tensile) strain,, i) Volume strain, () Shearing strain., Explain behaviour of wire under, continuously increasing load., Define, , 9, , State whether rubber is, , 4, 5., 6., , 7., , factor of, , safety., , more elastic or, steel, why ?, Define ultimate and, stress., breaking, 11. Define factor of, safety and elastic limit., 12. Define, Young's modulus, Bulk modulus and, , 10., , Rigidity modulus of elasticity. State relation between them., Distinguish between elastic bodies and plastic bodies., 14. Define: ) Stress, Gi) Strain, Gii) Restoring force, (iv), Deforming force., 15. Explain elastic limit and, yield point on stress-strain diagram., 13., , 16. State and explain Hooke's law. Define modulus of rigidity. Write down its S.I. unit, , 17., , State Hooke's law of, , 20., , Define: () Young's modulus Y, (i) Bulk modulus 'K, (Gii) Modulus, of rigidity'n'., , elasticity and define Young's modulus of elasticity., 18. Define deforming force and restoring force. State S.I. unit of stress., 19. State Hooke's law of elasticity and define elastic limit., , 21. Correct the equation, , Y, , =, , 9 Kn, , 3 (K+n), , 22. Define Poisson's ratio and state its formula., , B. T.E. Ques tions, Out, , ofsteel and, , rubber, which is, , elastic and, , why, Explain the behaviour of wire under continuously increasing load with the help of graph., Define stress and factor of safety., Define stress and strain., Define rigidity and stress., State and, , explain Hooke's, , more, , law of elasticity. Hence define elastic limit., , (S-06/2 M)D, , (S-06, 05, 03; W-02/4 M), W-04/2 M), S-05/2 M), (W-05/2 M), W-05/4 M)

Page 19 :
Applied Science: Physics (Mechanical)., , Properties of Matter and, , 1.18, , Non-Destructive Ta, , Testing, , (S-04/2 M), , Define the terms: (a) Young's modulus, (b) Yield point,, , 8., , Define modulus of rigidity. Give its units., , 9., , Define: (1) Elasticity, (2) Plasticity., , 10., , Define the term breaking stress., , S-02/4 M), , (S-03/3 M), , (W-02/2 M), , |Practice Problems, 1., , Calculate the strain, , produced, , in, , a, , wire under tension when its stress is 12x, , 105, , Y for material is 2, , kg/m,, , x, , 10° kg/m2, , Ans. Strain = 0.6., , A wire of diameter 4, , 2, , mm, , and of, , length, , 2, , m, , extends, , by, , 1.99, , mm, , applying, , a, , force of 10 N. Find Young's, , modulus of, , material of the wire., , Ans. Y 7.996 x 103 N/m2., 3., , Calculate the strain produced in a material if the stress is 2000 kg/cm2 and Y = 2 x 10 kg/cm-., Ans. Strain, , 4., , 103, , =, , A wire of length 1.S m extends by 1.5 mm when a force is applied to it. Calculate the stress produced in it, Given Y = 2x 1011, , N/m2, , Ans. Stress = 2x 10* N/m?., , 5., , A wire of length 1 m extends by 2 mm when stress acting on it is found to be 4000 kg/cm2. Find Young's modulus of, material of the wire., Ans. Y = 1.96 x 1011 N/m2., , 6., , 7, , A wire, , gets elongated by 0.002, , original length, , A steel wire of, , 314, , length, , cm, , lower end, find the extension, Ans. I= 04, mm., 8., , A, , weight exerts force, , wire is 5, Ans., , 9., , m, , (Y, , I= 1.5, , =, , x, , when a stress of 2000, of the wire is 4 m., , mm, , material of wire if the, , N/m, , is, , applied., , of 120 N, , on, , steel wire of, , 1013 N/m)., 105m, , Young's modulus, , of, , elasticity of, , (Ans.Y = 4x 10 N/m, , and diameter 1 mm has its, upper end tied to, produced in the wire. Y 1.96 x 1011 N/m2, , 2x, , Find, , a, , beam. If, , a, , load of 2 kg is attached, , to, , the, , cross-sectional area 0.02 cm2. Find extension produced if the length of, , Equal weights, , are attached to two wires of the, same metal. The, radius of the other wire. Calculate the ratio of their, extensions., , length, , and radius of, , one, , wire is twice the, , length and, , Ans. : 2 =1:2., 10., , Find the, ifY 2x, =, , Ans., 11., , weight attached, , When a metal cube is, subjected to, strain and bulk modulus of, Ans. Volume strain, , 12., , to the lower end of the wire, of, , 1011 N/m2., Weight =F 22.62 N., , a, , stress of 2, , 10 N/m,, , x, , metal, , length, , 1.5 m, radius 0.3, , each side of the cube is, , mm, , extends it by 0.6, , shortened by 29%. Find, , volume, , 0.059, Bulk modulus 3.39 x, 10 N/m., A metal cube of, volume 0.7 m is, to, a, subjected, block. Also calculate, pressure of 1.2 x 10°, metal. (Given: Bulk modulus of N/m. Calculate the change in volume of, of, metal K = 9x 100, meta, Ans. dv 9.33 x 10, m', Compressibility 0.11 x 1010, N/m), m/N, 8 cm thick, square metal plate has area 2 m., The lower surface of the, the top surface and the, plate is fixed and a, top surface, tangential force is applied, (Given: Modulus of rigidity of metal displaces by 0.06 mm. Calculate shearing stress,, strain., shearing, n 3.5 x 10*° N/m), Ans. Shearing strain 0.75 x, 10, Shearing stress 2.62 x, A metal wire of, 10' N/m?., 1.5 m and, length, diameter, 0.9, 1 mm and diameter, mm is stretched by a certain, of wire decreases, 0.12 x, by, 10 mm, calculate Poisson's load. If extension produced in the wireB, Ans. Poisson's ratio,, o 0.2., ratio of material of, wire., An, 3, mm, in, wire, wire if Young's modulus of diameter and 4 m long is used to, aluminium is 7 x 10 N/m 2?, support a mass of 50 kq., What is the, ofth, =, , =, , =, , compressibility, , =, , 13., , =, , =, , 14., , 15., , mm,, , =, , aluminium, , elongationo