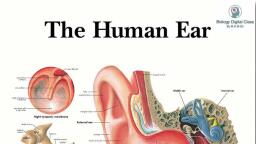
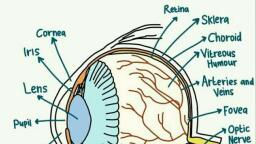
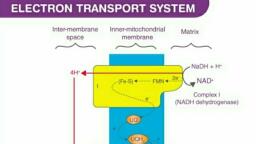
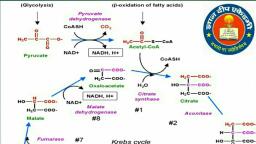
Page 1 :
Motion in One Dimension 73, , Chapter, , 2, , Motion In One Dimension, Position, Any object is situated at point O and three observers from three, different places are, N, O, looking at same, W, object, then all three, E, S, observers will have, B, different, C, 4m, observations about, 5m, A, the position of point, 3m, O and no one will, Fig. 2.1, be wrong. Because, they are observing, the object from different positions., Observer ‘A’ says : Point O is 3 m away in west direction., Observer ‘B’ says : Point O is 4 m away in south direction., Observer ‘C’ says : Point O is 5 m away in east direction., Therefore position of any point is completely expressed by two, factors: Its distance from the observer and its direction with respect to, observer., That is why position is characterised by a vector known as position, vector., Y, P(x,y,z), Consider a point P in xy plane and its, , , r, coordinates are (x, y). Then position vector (r ) of, X, point will be xˆi  yˆj and if the point P is in space, and its coordinates are (x, y, z) then position vector, , can be expressed as r  xˆi  yˆj  zkˆ ., , Z, , A passenger standing on platform observes that a tree on a platform is, at rest. But the same passenger passing away in a train through station,, observes that tree is in motion. In both conditions observer is right. But, observations are different because in first situation observer stands on a, platform, which is reference frame at rest and in second situation observer, moving in train, which is reference frame in motion., So rest and motion are relative terms. It depends upon the frame of, references., Table 2.1 : Types of motion, One dimensional, , Two dimensional, , Three dimensional, , Motion of a body in a, straight line is called, one dimensional, motion., , Motion of body in a, plane is called two, dimensional motion., , Motion of body in a, space is called three, dimensional motion., , When, only, one, coordinate, of, the, position of a body, changes with time then, it is said to be moving, one dimensionally., , When two coordinates, of the position of a, body changes with, time then it is said to, be, moving, two, dimensionally., , When, all, three, coordinates, of, the, position of a body, changes with time then, it is said to be moving, three dimensionally., , Ex.. (i) Motion of car on a, , Ex. (i) Motion of car on, , Ex.. (i) Motion of flying, , straight road., , a circular turn., , kite., , (ii) Motion of freely, falling body., , (ii) Motion of billiards, ball., , (ii) Motion of flying, insect., , Rest and Motion, , Particle or Point Mass or Point object, , If a body does not change its position as time passes with respect to, frame of reference, it is said to be at rest., , The smallest part of matter with zero dimension which can be, described by its mass and position is defined as a particle or point mass., If the size of a body is negligible in comparison to its range of motion, then that body is known as a particle., A body (Group of particles) can be treated as a particle, depends, upon types of motion. For example in a planetary motion around the sun, the different planets can be presumed to be the particles., , And if a body changes its position as time passes with respect to, frame of reference, it is said to be in motion., Frame of Reference : It is a system to which a set of coordinates are, attached and with reference to which observer describes any event.

Page 2 :
74 Motion in one Dimension, In above consideration when we treat body as particle, all parts of, the body undergo same displacement and have same velocity and, acceleration., , Distance and Displacement, (1) Distance : It is the actual length of the path covered by a moving, particle in a given interval of time., (i) If a particle starts from A and reach to C through point B as shown, in the figure., C, Then distance travelled by particle,  AB  BC  7 m, , (ii) Dimension : [M L T ], (iii) Unit : metre/second (S.I.), cm/second (C.G.S.), (iv) Types of speed :, (a) Uniform speed : When a particle covers equal distances in equal, intervals of time, (no matter how small the intervals are) then it is said to, be moving with uniform speed. In given illustration motorcyclist travels, equal distance (= 5m) in each second. So we can say that particle is moving, with uniform speed of 5 m/s., 0, , 1, , –1, , 4m, , (ii) Distance is a scalar quantity., (iii) Dimension : [M L T ], A, B, 3m, (iv) Unit : metre (S.I.), (2) Displacement : Displacement is the change in Fig., position, vector, i.e., A, 2.2, vector joining initial to final position., (i) Displacement is a vector quantity, (ii) Dimension : [M L T ], (iii) Unit : metre (S.I.), (iv) In the above figure the displacement of the particle, 0, , 0, , (i) It is a scalar quantity having symbol  ., , 1, , 1, , 0, , 0, ,  ( AB) 2  (BC) 2  2( AB) (BC) cos 90 o = 5 m,   , , (v) If S 1 , S 2 , S 3 ........ S n are the displacements of a body then the, , total (net) displacement is the vector sum of the individuals.,  , , , , S  S 1  S 2  S 3  ........  S n, (3) Comparison between distance and displacement :, (i) The magnitude of displacement is equal to minimum possible, distance between two positions., So distance  |Displacement|., (ii) For a moving particle distance can never be negative or zero while, displacement can be., (zero displacement means that body after motion has came back to, initial position), i.e., Distance > 0 but Displacement > = or < 0, (iii) For motion between two points, displacement is single valued, while distance depends on actual path and so can have many values., (iv) For a moving particle distance can never decrease with time while, displacement can. Decrease in displacement with time means body is, moving towards the initial position., (v) In general, magnitude of displacement is not equal to distance., However, it can be so if the motion is along a straight line without change, in direction., Y, , , (vi) If rA and rB are the position, B, s, vectors of particle initially and finally., P, Then displacement of the particle, , , , , , rAB, A, rAB  rB  rA, rB, , , rA, X, , Speed and Velocity, (1) Speed : The rate of distance, covered with time is called speed., , 5m, , 5m, , 5m, , 5m, , 1 sec, , 1 sec, , 1 sec, , 1 sec, , 1 sec, , 5m/s, , Uniform Speed, , 5m/s, , 5m/s, , 5m/s, , 5m, 1m/s, , 5m/s, , 5m/s, , (b) Non-uniform (variable) speed : In non-uniform speed particle, Fig. 2.4, covers unequal distances in equal intervals of time. In the given illustration, motorcyclist travels 5m in 1 second, 8m in 2 second, 10m in 3 second, 4m, in 4 second etc., st, , nd, , rd, , th, , Therefore its speed is different for every time interval of one second., This means particle is moving with variable speed., , AC  AB  BC  | AC |, , and s is the distance travelled if the, particle has gone through the path APB., , Time, , 5m, , Fig. 2.3, , Distance, Time, , 5m, , 8m, , 10m, , 4m, , 6m, , 7m, , 1 sec, , 1 sec, , 1 sec, , 1 sec, , 1 sec, , 1 sec, , 5m/s, , Variable Speed, , 8m/s, , 10m/s, , 4m/s, , 6m/ s, , 7m/ s, , Fig. 2.5of a particle for a given ‘Interval, (c) Average speed : The average speed, of time’ is defined as the ratio of total distance travelled to the time taken., s, Total distance travelled, Average speed , ; v av , t, Time taken,  Time average speed : When particle moves with different uniform, speed  1 ,  2 ,  3 ... etc in different time intervals t1 , t 2 , t 3 , ... etc, respectively, its average speed over the total time of journey is given as, Total distance covered, vav , Total time elapsed, , , , d 1  d 2  d 3  ......,  t   2 t 2   3 t 3  ......, = 11, t1  t 2  t 3  ......, t1  t 2  t 3  ......, ,  Distance averaged speed : When a particle describes different, distances d 1 , d 2 , d 3 , ...... with different time intervals t1 , t 2 , t 3 , ......, with speeds v1 , v 2 , v 3 ...... respectively then the speed of particle averaged, over the total distance can be given as, d  d 2  d 3  ......, Total distance covered,  1,  av , t1  t 2  t 3  ......, Total time elapsed, , , d 1  d 2  d 3  ......, d1 d 2 d 3, , ,  ......, , 1, , , 2, , 3, , If speed is continuously changing with time then, v av , ,  vdt,  dt

Page 3 :
Motion in One Dimension 75, (d) Instantaneous speed : It is the speed of a particle at a particular, instant of time. When we say ‚speed‛, it usually means instantaneous speed., The instantaneous speed is average speed for infinitesimally small time, interval (i.e., t  0 ). Thus, s ds, , t, dt, (2) Velocity : The rate of change of position i.e. rate of displacement, with time is called velocity., , (i) It is a vector quantity having symbol v ., (ii) Dimension : [M L T ], (iii) Unit : metre/second (S.I.), cm/second (C.G.S.), (iv) Types of velocity :, (a) Uniform velocity : A particle is said to have uniform velocity, if, magnitudes as well as direction of its velocity remains same and this is, possible only when the particles moves in same straight line without, reversing its direction., (b) Non-uniform velocity : A particle is said to have non-uniform, velocity, if either of magnitude or direction of velocity changes or both of, them change., (c) Average velocity : It is defined as the ratio of displacement to time, taken by the body, , , Displacement, r, ; v av , Average velocity , Time taken, t, (d) Instantaneous velocity : Instantaneous velocity is defined as rate of, change of position vector of particles with time at a certain instant of time., , , , r, dr, Instantaneous velocity v  lim, , t  0 t, dt, (v) Comparison between instantaneous speed and instantaneous, velocity, (a) instantaneous velocity is always tangential to the path followed by, the particle., When a stone is thrown from point O then at point of projection the, , instantaneous velocity of stone is v1 , at point A the instantaneous velocity, , , , of stone is v 2 , similarly at point B and C are v 3 and v 4 respectively., , Instantaneous speed v  lim, , t 0, , 0, , 1, , –1, , Y, , v3, , , v2, , A, , v1, O, , B, C, , , v4, , For the given value of t, we can find out the instantaneous velocity., , e.g for t  0 ,Instantaneous velocity v   A1 and Instantaneous, , speed | v |  A1, (vi) Comparison between average speed and average velocity, (a) Average speed is a scalar while average velocity is a vector, both having same units ( m/s) and dimensions [LT 1 ] ., (b) Average speed or velocity depends on time interval over which it is, defined., (c) For a given time interval average velocity is single valued while, average speed can have many values depending on path followed., (d) If after motion body comes back to its initial position then, , , vav  0 (as r  0 ) but vav  0 and finite as (s  0) ., (e) For a moving body average speed can never be negative or zero, , (unless t  ) while average velocity can be i.e. v av  0 while v a = or <, 0., (f) As we know for a given time interval, Distance  |displacement|,  Average speed  |Average velocity|, , Acceleration, The time rate of change of velocity of an object is called acceleration, of the object., (1) It is a vector quantity. It’s direction is same as that of change in, velocity (Not of the velocity), Table 2.2 : Possible ways of velocity change, When only direction of, velocity changes, , When only magnitude, of velocity changes, , When both magnitude, and direction of, velocity changes, , Acceleration, perpendicular to, velocity, , Acceleration parallel or, anti-parallel to velocity, , Acceleration has two, components one is, perpendicular to, velocity and another, parallel or anti-parallel, to velocity, , Ex.. Uniform circular, , Ex.., , Ex.. Projectile motion, , motion, , gravity, , Motion, , under, , (2) Dimension : [M L T ], 0, , 1, , –2, , (3) Unit : metre/second (S.I.); cm/second (C.G.S.), 2, , X, , Direction of these velocities can beFig.found, 2.6 out by drawing a tangent on, the trajectory at a given point., (b) A particle may have constant instantaneous speed but variable, instantaneous velocity., Example : When a particle is performing uniform circular motion then, for every instant of its circular motion its speed remains constant but, velocity changes at every instant., (c) The magnitude of instantaneous velocity is equal to the, instantaneous speed., (d) If a particle is moving with constant velocity then its average, velocity and instantaneous velocity are always equal., (e) If displacement is given as a function of time, then time derivative, of displacement will give velocity., , x  A0  A1 t  A2 t 2, Let displacement, ,  dx, d,  ( A0  A1 t  A2 t 2 ), Instantaneous velocity v , dt dt, , v   A1  2 A2 t, , 2, , (4) Types of acceleration :, (i) Uniform acceleration : A body is said to have uniform, acceleration if magnitude and direction of the acceleration remains constant, during particle motion., (ii) Non-uniform acceleration : A body is said to have non-uniform, acceleration, if either magnitude or direction or both of them change during, motion.,  , , , v v 2  v1, (iii) Average acceleration : aa , , t, t, The direction of average acceleration vector is the direction of the, ,  v, change in velocity vector as a , t, , , , v d v, (iv) Instantaneous acceleration = a  lim, , t 0 t, dt

Page 4 :
76 Motion in one Dimension, (v) For a moving body there is no relation between the direction of, instantaneous velocity and direction of acceleration., , , 2, , 1, , , a, , Position time Graph, , , , a, g, , , to ‚g‛, where g is the acceleration due to gravity. Its value is 9.8 m/s 2 or, 980 cm/s 2 or 32 feet/s 2 ., , Y, , a, , , (xii) For motion of a body under gravity, acceleration will be equal, , , , g, , g, , , , During motion of the particle its parameters of kinematical analysis, (v, a, s) changes with time. This can be represented on the graph., 3, , X, , O, , Position time graph is plotted by taking time t along x-axis and, position of the particle on y-axis., y, , Fig. 2.7, , (b) In a projectile motion  is variable for every point of trajectory., (vi) If a force F acts on a particle of mass m, by Newton’s 2 law,, ,  F, acceleration a , m, nd, , Position, , Ex.. (a) In uniform circular motion  = 90º always, , y1, , , , ,  dx ,  dv d 2 x , (vii) By definition a ,  2  As v , dt , dt, dt , , i.e., if x is given as a function of time, second time derivative of, displacement gives acceleration, (viii) If velocity is given as a function of position, then by chain rule, a, , dv dv dx, d, , ,  v., dt, dx dt, dx, , dx , , as v  dt , , , , D, , y2, , O, , B, , , A, , t1, , x, , t2, Time, , Let AB is a position-time graph, for any moving particle, Fig. 2.8, As Velocity =, , Change in position y 2  y 1, , Time taken, t 2  t1, , From triangle ABC, tan  , , (xi) Acceleration can be positive, zero or negative. Positive, acceleration means velocity increasing with time, zero acceleration means, velocity is uniform constant while negative acceleration (retardation) means, velocity is decreasing with time., , C, , BC AD y 2  y 1, , , AC AC, t 2  t1, , …(i), , ….(ii), , By comparing (i) and (ii) Velocity = tan, , v = tan, It is clear that slope of tangent on position-time graph represents, the velocity of the particle., , Table 2.3 : Various position -time graphs and their interpretation

Page 5 :
Motion in One Dimension 77, P,  = 0° so v = 0, , i.e., line parallel to time axis represents that the particle is at rest., O, , T, , P,  = 90° so v = , , O, , i.e., line perpendicular to time axis represents that particle is changing its position but time does not changes it, means the particle possesses infinite velocity., , T, , Practically this is not possible., , P,  = constant so v = constant, a = 0, i.e., line with constant slope represents uniform velocity of the particle., , O, , T, , P,  is increasing so v is increasing, a is positive., i.e., line bending towards position axis represents increasing velocity of particle. It means the particle possesses, acceleration., , O, , T, , P,  is decreasing so v is decreasing, a is negative, i.e., line bending towards time axis represents decreasing velocity of the particle. It means the particle possesses, O, , retardation., , T, , P,  constant but > 90o so v will be constant but negative, i.e., line with negative slope represent that particle returns towards the point of reference. (negative displacement)., , , O, P, A, , B, , T, C, , O, P, , Straight line segments of different slopes represent that velocity of the body changes after certain interval of time., , T, , S, , This graph shows that at one instant the particle has two positions, which is not possible., , T, , O, , P, The graph shows that particle coming towards origin initially and after that it is moving away from origin., , Note : , , T, , If the graph is plotted between distance and time then, , it is always an increasing curve and it never, comes back towards origin because distance, never decrease with time. Hence such type, of distance time graph is valid up to point A, only, after point A, it is not valid as shown, in the figure., , Velocity-time Graph, The graph is plotted by taking time t, , A, , Distance, , O, , along x-axis and velocity of the particle on y-axis., Calculation of Distance and displacement : The area covered, between the velocity time graph and time axis gives the displacement and, distance travelled by the body for a given time interval., Total distance | A1 | | A2 | | A3 |, = Addition of modulus of different area. i.e. s  |  | dt, , O, , Time, Fig. 2.9, , Total displacement  A1  A2  A3, = Addition of different area considering their sign.

Page 6 :
78 Motion in one Dimension, i.e. r    dt, Area above time axis is taken as positive, while area below time axis, is taken as negative, +, , As Acceleration =, 1, , 3, , , , t, 2, , Change in velocity, Time taken, , v 2  v1, t2  t1, , From triangle ABC, tan  , , –, Fig. 2.10, , , , Calculation of Acceleration : Let AB is a velocity-time graph for any, moving particle, , By comparing (i) and (ii), , 2, , 3, , Velocity, , ….(ii), , Acceleration (a) = tan , It is clear that slope of tangent on velocity-time graph represents the, acceleration of the particle., , y, v2, , D, , B, , , v1, A, O, , BC AD, , AC AC, , v 2  v1, t2  t1, , here A and A are area of triangle 1 and 2 respectively and A is the, area of trapezium ., 1, , …(i), , C, , x, Table, t2 2.4 : Various velocity -time graphs and their interpretation, , t1, Time, Fig. 2.11, , Velocity, ,  = 0°, a = 0, v = constant, i.e., line parallel to time axis represents that the particle is moving with constant velocity., , O, , Velocity, ,  = 90o, a = , v = increasing, i.e., line perpendicular to time axis represents that the particle is increasing its velocity, but time does, not change. It means the particle possesses infinite acceleration. Practically it is not possible., , O, , Time, , Velocity, ,  = constant, so a = constant and v is increasing uniformly with time, i.e., line with constant slope represents uniform acceleration of the particle., , O, , Time, , Velocity, ,  increasing so acceleration increasing, i.e., line bending towards velocity axis represent the increasing acceleration in the body., O, , Time, , Velocity, ,  decreasing so acceleration decreasing, , O, , Time

Page 7 :
Motion in One Dimension 79, , Velocity, , i.e. line bending towards time axis represents the decreasing acceleration in the body, , Positive constant acceleration because  is constant and < 90o but initial velocity of the particle is, negative., , O, , Time, , Velocity, , Positive constant acceleration because  is constant and < 90o but initial velocity of particle is positive., , O, , Time, , Velocity, , Negative constant acceleration because  is constant and > 90o but initial velocity of the particle is, positive., , O, , Time, , Velocity, , Negative constant acceleration because  is constant and > 90o but initial velocity of the particle is zero., , Time, , Velocity, , O, , O, , Negative constant acceleration because  is constant and > 90o but initial velocity of the particle is, negative., Time, , (2) When particle moves with constant acceleration, , Equation of Kinematics, These are the various relations between u, v, a, t and s for the particle, moving with uniform acceleration where the notations are used as :, , u = Initial velocity of the particle at time t = 0 sec, v = Final velocity at time t sec, , (i) Acceleration is said to be constant when both the magnitude and, direction of acceleration remain constant., (ii) There will be one dimensional motion if initial velocity and, acceleration are parallel or anti-parallel to each other., (iii) Equations of motion, , a = Acceleration of the particle, , (in scalar from), , s = Distance travelled in time t sec, s = Distance travelled by the body in n sec, th, ,   u  at, , Equation of motion, (in vector from),   , v  u  at, , n, , (1) When particle moves with zero acceleration, (i) It is a unidirectional motion with constant speed., (ii) Magnitude of displacement is always equal to the distance, travelled., (iii) v = u,, , s=ut, , [As a = 0], , s  ut , , 1 2, at, 2, ,   1, s  u t  at 2, 2, ,  2  u 2  2as, ,  , , v .v  u.u  2a.s, , u v , s, t,  2 , ,  1  , s  (u  v ) t, 2

Page 8 :
80 Motion in one Dimension, sn  u , , , ,  a, sn  u  (2n  1), 2, , a, (2n  1), 2, , (2) If a body is projected vertically downward with some initial, velocity, , The force of attraction of earth on bodies, is called force of, gravity. Acceleration produced in the body by the force of gravity, is, called acceleration due to gravity. It is represented by the symbol g ., In the absence of air resistance, it is found that all bodies, (irrespective of the size, weight or composition) fall with the same, acceleration near the surface of the earth. This motion of a body falling, towards the earth from a small altitude (h << R) is called free fall., An ideal example of one-dimensional motion is motion under gravity, in which air resistance and the small changes in acceleration with height are, neglected., (1) If a body is dropped from some height (initial velocity zero), (i) Equations of motion : Taking initial position as origin and, direction of motion (i.e., downward direction) as a positive, here we have, , h  ut , , 1 2, gt, 2, ,  2  u 2  2 gh, g, (2n  1), 2, (3) If a body is projected vertically upward, (i) Equation of motion : Taking initial position as origin and, direction of motion (i.e., vertically up) as positive, a = – g [As acceleration is downwards while motion upwards], So, if the body is projected with velocity u and after time t it, reaches up to height h then, hn  u , ,   u  g t ; h  ut , , 1 2 2, g, g t ;   u 2  2 gh ; hn  u  (2n  1), 2, 2, , (ii) For maximum height v = 0, , u=0, , So from above equation u = gt,, 2h, , t , , g, v , , h, ,  u  gt, , Equation of motion :, , Motion of Body Under Gravity (Free Fall), , , , v, , h, , g, , and, , 2 gh, , v, , h , , 1 2, gt, 2, v=0, , u 2  2 gh, , 2, , u, g, , u, u , , v, , [As body starts from rest], [As acceleration, is in the direction of motion], Fig. 2.12, …(i), , h, , 2 gh, , u, , 2, , 2g, , 1 2, gt, 2, , …(ii), ,  2  2 gh, , …(iii), , h, , , , g, , h, , 2g, , u=0, a = +g, v=gt, , 2h, , t , , g, ...(iv), (2n  1), 2, (ii) Graph of distance, velocity and acceleration with respect to time, hn , , (iii) Graph of displacement,, and acceleration with respect to, Fig.velocity, 2.14, time (for maximum height) :, s, , (u2/2g), , v, +, , :, , (u/g), , O, s, , v, , a, , (2u/g), , t, , –, , (u/g), , g, tan = g, , a, , –v, , t, , , t, , t, , t, , 2.13, (iii) As h = (1/2)gt , i.e., h  Fig., t , distance, covered in time t, 2t, 3t, etc.,, will be in the ratio of 1 : 2 : 3 , i.e., square of integers., 2, , 2, , 2, , 2, , +, , O, , t, , g, , 2, , 1, (iv) The distance covered in the nth sec, hn  g (2n  1), 2, , So distance covered in 1 , 2 , 3 sec, etc., will be in the ratio of 1 : 3 :, 5, i.e., odd integers only., st, , nd, , rd, , –a, Fig. 2.15, , It is clear that both quantities do not depend upon the mass of the, body or we can say that in absence of air resistance, all bodies fall on the, surface of the earth with the same rate.

Page 9 :
Motion in One Dimension 81, (4) The motion is independent of the mass of the body, as in any, equation of motion, mass is not involved. That is why a heavy and light, body when released from the same height, reach the ground simultaneously, , a = f (v), , then t , , dv, , vdv, , v, v,  u f (v) and x  x 0  u f (v), , and with same velocity i.e., t  (2h / g) and v  2 gh ., (5) In case of motion under gravity, time taken to go up is equal to, the time taken to fall down through the same distance. Time of descent ( t ), = time of ascent (t ) = u/g, 2, , 1, ,  Total time of flight T = t + t , 1, , 2, ,  During translational motion of the body, there is change in the, , 2u, g, , location of the body., , (6) In case of motion under gravity, the speed with which a body is, projected up is equal to the speed with which it comes back to the point of, projection., As well as the magnitude of velocity at any point on the path is same, whether the body is moving in upwards or downward direction., (7) A body is thrown vertically upwards. If air resistance is to be, taken into account, then the time of ascent is less than the time of descent., t >t, 2, ,  During rotational motion of the body, there is change in the, orientation of the body, while there is no change in the location of the, body from the axis of rotation., ,  A point object is just a mathematical point. This concept is, introduced to study the motion of a body in a simple manner., ,  The choice of the origin is purely arbitrary.,  For one dimensional motion the angle between acceleration and, velocity is either 0° or 180° and it does not change with time., , 1, , Let u is the initial velocity of body then time of ascent t1 , and h , , u, ga, , u2, 2(g  a), , For downward motion a and g will work in opposite direction, because a always work in direction opposite to motion and g always work, vertically downward., , , , , , the angle between a and v lies between –90° and +90°., ,  The particle speeds down, that is the speed of the particle, , , , decreases, when the angle between a and v lies between +90° and, 270°., ,  The speed of the particle remains constant when the angle between, , , a and v is equal to 90°., , 1, (g  a) t22, 2, ,  The distance covered by a particle never decreases with time, it, always increases., , 2, , u, 1,  (g  a) t22, 2(g  a) 2, ,  t2 , , velocity is other than 0° or 180° and also it may change with time., , ,  If the angle between a and v is 90°, the path of the particle is a, circle., ,  The particle speed up, that is the speed of the particle increases when, , where g is acceleration due to gravity and a is retardation by air, resistance and for upward motion both will work vertically downward., , So h , ,  For two dimensional motion, the angle between acceleration and, ,  Displacement of a particle is the unique path between the initial, and final positions of the particle. It may or may not be the actually, travelled path of the particle., , u, ,  Displacement of a particle gives no information regarding the, , (g  a)(g  a), , nature of the path followed by the particle., Comparing t and t we can say that t > t, ,  Magnitude of displacement  Distance covered., , since (g + a ) > (g – a), ,  Since distance  |Displacement|, so average speed of a body is equal, , 1, , 2, , 2, , 1, , Motion with Variable Acceleration, (i) If acceleration is a function of time, , or greater than the magnitude of the average velocity of the body., ,  The average speed of a body is equal to its instantaneous speed if, the body moves with a constant speed, , a  f (t), , then v  u   0 f (t) dt, ,  No force is required to move the body or an object with uniform, , and s  ut , , t, ,    f (t) dt dt, ,  Velocity of the body is positive, if it moves to the right side of the, , 0, , origin. Velocity is negative if the body moves to the left side of the, origin., , t, , (ii) If acceleration is a function of distance, a  f (x ), , x, , then v  u  2  x f (x ) dx, 2, , 2, , 0, , (iii) If acceleration is a function of velocity, , velocity., ,  When a particle returns to the starting point, its displacement is, zero but the distance covered is not zero., ,  When a body reverses its direction of motion while moving along a, straight line, then the distance travelled by the body is greater than the, magnitude of the displacement of the body. In this case, average speed of

Page 10 :
82 Motion in one Dimension, the body is greater than its average velocity., As  2  u 2  2as  0  u 2  2as  s , ,  Speedometer measures the instantaneous speed of a vehicle., , u2, , s  u2, 2a, , [since a is constant], ,  When particle moves with speed v upto half time of its total, 1, , motion and in rest time it is moving with speed v then v av , 2, , v1  v 2, 2, , So we can say that if u becomes n times then s becomes n times that of, previous value., 2, ,  When particle moves the first half of a distance at a speed of v and, 1, , second half of the distance at speed v then, v av, ,  A particle moving with uniform acceleration from A to B along a, straight line has velocities  1 and  2 at A and B respectively. If C is, , 2, , 2v1v 2, , v1  v 2, , the mid-point between A and B then velocity of the particle at C is equal, to, ,  When particle covers one-third distance at speed v, next one third at, 1, , , , speed v and last one third at speed v, then, 2, , v av, , 3, , 3 v1 v 2 v 3, , v1 v 2  v 2 v 3  v 3 v1, , 2, ,  The body returns to its point of projection with the same, ,  For two particles having displacement time graph with slopes , 1, , 1, , 1 tan 1, ,  2 tan  2, , and  possesses velocities v and v respectively then, 2, ,  12   22, , 2, , magnitude of the velocity with which it was thrown vertically upward,, provided air resistance is neglected., ,  All bodies fall freely with the same acceleration., ,  Velocity of a particle having uniform motion = slope of, ,  The acceleration of the falling bodies does not depend on the mass, , displacement–time graph., , of the body., ,  Greater the slope of displacement-time graph, greater is the, ,  If two bodies are dropped from the same height, they reach the, , velocity and vice-versa., , ground in the same time and with the same velocity., ,  Area under v – t graph = displacement of the particle., ,  If a body is thrown upwards with velocity u from the top of a, ,  Slope of velocity-time graph = acceleration., , tower and another body is thrown downwards from the same point and, with the same velocity, then both reach the ground with the same speed., ,  If a particle is accelerated for a time t with acceleration a and for, 1, , time, aa, , t, , with acceleration, a1 t1  a2 t2, , t1  t2, 2, , a, , then, , 2, , 1, , average, , acceleration, , is, ,  When a particle returns to the starting point, its average velocity is, zero but the average speed is not zero., ,  If same force is applied on two bodies of different masses m1 and, m 2 separately then it produces accelerations a1 and a 2 respectively., Now these bodies are attached together and form a combined system, and same force is applied on that system so that a be the acceleration of, the combined system, then, , If both the objects A and B move along parallel lines in the, same direction, then the relative velocity of A w.r.t. B is given by v =, v –v, , , AB, , A, , B, , and the relative velocity of B w.r.t. A is given by v = v – v, BA, , B, , A, ,  If both the objects A and B move along parallel lines in the, opposite direction, then the relative velocity of A w.r.t. B is given by v =, v – (– v ) = v + v, AB, , a a, a 1 2, a1  a 2, , A, , B, , A, , B, , and the relative velocity of B w.r.t. A is given by v = – v – v, BA, ,  If a body starts from rest and moves with uniform acceleration, then distance covered by the body in t sec is proportional to t (i.e., 2, , s  t 2 )., , So we can say that the ratio of distance covered in 1 sec, 2 sec, 2, , 2, , 2, , and 3 sec is 1 : 2 : 3 or 1 : 4 : 9., ,  If a body starts from rest and moves with uniform acceleration, then distance covered by the body in nth sec is proportional to (2n  1), (i.e. s n  (2n –1)), So we can say that the ratio of distance covered in 1 , 2 and 3 is 1 : 3 : 5., st, , nd, , rd, ,  A body moving with a velocity u is stopped by application of, brakes after covering a distance s. If the same body moves with, velocity nu and same braking force is applied on it then it will come, to rest after covering a distance of n s., 2, , B, , A, ,  Suppose a body is projected upwards from the ground and with, the velocity u. It is assumed that the friction of the air is negligible. The, characteristics of motion of such a body are as follows., (i) The maximum height attained = H = u /2g., 2, , (ii) Time taken to go up (ascent) = Time taken to come down (descent), = t = u/g., (iii) Time of flight T = 2t = 2u/g., (iv) The speed of the body on return to the ground = speed with which, it was thrown upwards., (v) When the height attained is not large, that is u is not large, the mass,, the weight as well as the acceleration remain constant with time. But its, speed, velocity, momentum, potential energy and kinetic energy change, with time., (vi) Let m be the mass of the body. Then in going from the ground to, the highest point, following changes take place.

Page 11 :
Motion in One Dimension 83, (a) Change in speed = u, (b) Change in velocity = u, (c) Change in momentum = m u, (d) Change in kinetic energy = Change in potential energy, (1/2) mu ., , =, , 2, , (vii) On return to the ground the changes in these quantities are as, follows, (a) Change in speed = 0, (b) Change in velocity = 2u, (c) Change in momentum = 2mu, (d) Change in kinetic energy = Change in potential energy = 0, (viii) If, the friction of air be taken into account, then the motion of the, object thrown upwards will have the following properties, (a) Time taken to go up (ascent) < time taken to come down (descent), (b) The speed of the object on return to the ground is less than the, initial speed. Same is true for velocity (magnitude), momentum, (magnitude) and kinetic energy., (c) Maximum height attained is less than u /2g., 2, , (d) A part of the kinetic energy is used up in overcoming the friction., ,  A ball is dropped from a building of height h and it reaches after t, seconds on earth. From the same building if two balls are thrown (one, upwards and other downwards) with the same velocity u and they reach, the earth surface after t and t seconds respectively then, 1, , 2, , t  t1 t 2, ,  A particle is dropped vertically from rest from a height. The time, taken by it to fall through successive distance of 1m each will then be in, the ratio of the difference in the square roots of the integers i.e., 1 , ( 2  1 ), ( 3  2 ).......(, , 4  3 ),........ .