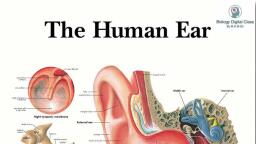
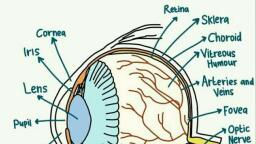
Page 1 :
Electrostatics 253, , Chapter, , 6, , Work, Energy, Power and Collision, Thus work done by a force is equal to the scalar (or dot product) of, the force and the displacement of the body., , Introduction, The terms 'work', 'energy' and 'power' are frequently used in, everyday language. A farmer clearing weeds in his field is said to be working, hard. A woman carrying water from a well to her house is said to be, working. In a drought affected region she may be required to carry it over, large distances. If she can do so, she is said to have a large stamina or, energy. Energy is thus the capacity to do work. The term power is usually, associated with speed. In karate, a powerful punch is one delivered at great, speed. In physics we shall define these terms very precisely. We shall find, that there is a loose correlation between the physical definitions and the, physiological pictures these terms generate in our minds., , If a number of forces F 1 , F 2 , F 3 ...... F n are acting on a body and, it shifts from position vector r 1 to position vector r, , Nature of Work Done, Positive work, Positive work means that force (or its component) is parallel to, displacement, Direction of motion, , F, , , s, , Work Done by a Constant Force, , By resolving force F into two components :, , then, , W  (F 1  F 2  F 3  .... F n ).( r 2  r 1 ), , Work is said to be done when a force applied on the body displaces, the body through a certain distance in the direction of force., , Let a constant force F be applied on the body such that it makes, an angle  with the horizontal and body is displaced through a distance s, , 2, , 0 o    90 o, , Fig. 6.2, , The positive work signifies that the external force favours the, motion of the body., Example: (i) When a person lifts a body from the ground, the work, done by the (upward) lifting force is positive, , (i) F cos in the direction of displacement of the body., (ii) F sin in the perpendicular direction of displacement of the body., , F man, , F sin, F, , s, , , F cos, s, , Since body is being displacedFig., in 6.1, the direction of F cos , therefore, work done by the force in displacing the body through a distance s is given, by, W  (F cos ) s  Fs cos, or W  F.s, , 6.3 by applying a force along the, (ii) When a lawn roller is Fig., pulled, handle at an acute angle, work done by the applied force is positive., , F, , s, , (iii) When a spring is stretched, work done by the external, Fig. 6.4, (stretching) force is positive., , s, F, Fig. 6.5, , s, F

Page 2 :
254 Work, Energy, Power and Collision, , Fg, , Maximum work : Wmax  F s, , s, , When cos   maximum  1 i.e.   0 o, It means force does maximum work when angle between force and, displacement is zero., Negative work, Negative work means that force (or its component) is opposite to, displacement i.e., , (ii) When a body is made Fig., to 6.7, slide over a rough surface, the work, done by the frictional force is negative., Minimum work : Wmin   F s, , Direction of motion, , F, , F, +, , , , s, , +, , s, , 90 o    180 o, , Fig. 6.8, , When cos  minimum  1 i.e   180 o, , Fig. 6.6, , The negative work signifies that the external force opposes the, motion of the body., Example: (i) When a person lifts a body from the ground, the work, done by the (downward) force of gravity is negative., , It means force does minimum [maximum negative] work when, angle between force and displacement is 180 ., o, , (iii) When a positive charge is moved towards another positive, charge. The work done by electrostatic force between them is negative., , Zero work, Under three condition, work done becomes zero W  Fs cos  0, (1) If the force is perpendicular to the displacement [ F  s ], , Example: (i), , When a coolie travels on a horizontal platform with a load on his head, work, done against gravity by the coolie is zero., , s, , (ii) When a body moves in a circle the work done by the centripetal force is, always zero., , Fg, , (iii) In case of motion of a charged particle in a magnetic field as force, [F  q(v  B)] is always perpendicular to motion, work done by this force is, , always zero., (2) If there is no displacement [s = 0], , Example: (i), , When a person tries to displace a wall or heavy stone by applying a force and it, does not move, then work done is zero., , F, s, , (ii) A weight lifter does work in lifting the weight off the ground but does not work, in holding it up., , 0, , (3) If there is no force acting on the body [F = 0], , Example: Motion of an isolated body in free space., , Work Done by a Variable Force, , The total work done in going from A to B as shown in the figure is, , When the magnitude and direction of a force varies with position,, the work done by such a force for an infinitesimal displacement is given by, , W  A F. d s  A (F cos  )ds, , dW  F. d s, , B, ds, , , F, , B, , B, , In terms of rectangular component F  Fx ˆi  Fy ˆj  Fz kˆ, d s  dxˆi  dyˆj  dzkˆ, B,  W  A (Fx ˆi  Fy ˆj  Fz kˆ ).(dxˆi  dyˆj  dzkˆ ), x, , y, , z, , or W  x B Fx dx  y B Fy dy  z B Fz dz, A, Fig. 6.9, , A, , A, , A

Page 3 :
Work, Energy, Power and Collision 255, , Work Done in Conservative and, , Dimension and Units of Work, Dimension : As work = Force  displacement, , Non-conservative Field, (1) In conservative field, work done by the force (line integral of the, , [W]  [MLT 2 ]  [L]  [ML2 T 2 ], Units : The units of work are of two types, , points., , Absolute units, , Gravitational units, , Joule [S.I.]: Work done is said to be, one Joule, when 1 Newton force, displaces the body through 1 metre in, , kg-m [S.I.]: 1 kg-m of work is, done when a force of 1kg-wt., displaces the body through 1m, , its own direction., , in its own direction., , From, W = F.s, , From, , 1 Joule = 1 Newton 1 m, , 1 kg-m = 1 kg-wt  1 m, , W AB  W AB  W AB, Path I, , or, , From W = F s, 1 erg  1dyne  1cm, , Relation between Joule and erg, 1 Joule = 1 N  1 m, , B, II, , Path II, , Path III, , III, Fig. 6.11, , (2) In conservative field work done by the force (line integral of the force, , i.e.  F.d l ) over a closed path/loop is zero., WAB  WB A  0,  , or  F.d l  0, , gm-cm [C.G.S.] : 1 gm-cm of, work is done when a force of, 1gm-wt displaces the body, through 1cm in its own, direction., From W = F s, 1 gm-cm = 1gm-wt  1cm. = 981, dyne  1cm, = 981 erg, , = 10 dyne  10 cm, 5, , I, , A, , Path III, ,  F.d l   F.d l   F.d l, Path I, , = 9.81 Joule, , its own direction., , Path II, , W=Fs, , = 9.81 N  1 metre, , erg [C.G.S.] : Work done is said to, be one erg when 1 dyne force, displaces the body through 1 cm in, ,  F.d l ) is independent of the path followed between any two, , force i.e., , A, , B, , Fig. 6.12, , Conservative force : The forces of these type of fields are known as, conservative forces., Example : Electrostatic forces, gravitational forces, elastic forces,, magnetic forces etc and all the central forces are conservative in nature., If a body of mass m lifted to height h from the ground level by, different path as shown in the figure, , 2, , B, , B, , B, , B, , = 10 dyne  cm = 10 erg, 7, , 7, , Work Done Calculation by Force Displacement, Graph, Let a body, whose initial position is x i , is acted upon by a variable, force (whose magnitude is changing continuously) and consequently the, body acquires its final position x f ., Force, , I, , II, , III, , l, , , A, , A, , IV, , h1, , h2, , h, , h3, , A, , A, , Work done through different, Fig.paths, 6.13, , , F, , WI  F. s  mg  h  mgh, , O, , h,  mgh, sin, WIII  mgh1  0  mgh2  0  mgh3  0  mgh4, WII  F. s  mg sin  l  mg sin , , xi, x, , xf, dx, , Displacement, , Let F be the average value of Fig., variable, 6.10 force within the interval dx, from position x to (x + dx) i.e. for small displacement dx. The work done, will be the area of the shaded strip of width dx. The work done on the body, in displacing it from position x i to x f will be equal to the sum of areas, dW  F dx, , , , xf, , xi, , dW , , WIV   F. d s  mgh, , It is clear that WI  WII  WIII  WIV  mgh ., Further if the body is brought back to its initial position A, similar, amount of work (energy) is released from the system, it means, WAB  mgh and WBA  mgh ., , of all the such strips, , W , ,  mg(h1  h2  h3  h4 )  mgh, , , , xf, , F dx, , xi, , x, , W  x f (Area of stripof widthdx ), i, , W  Area under curve between x i and x f, , i.e. Area under force-displacement curve with proper algebraic sign, represents work done by the force., , Hence the net work done against gravity over a round trip is zero., WNet  WAB  WBA  mgh  (mgh)  0, , i.e. the gravitational force is conservative in nature., Non-conservative forces : A force is said to be non-conservative if, work done by or against the force in moving a body from one position to, another, depends on the path followed between these two positions and for, complete cycle this work done can never be zero.

Page 4 :
256 Work, Energy, Power and Collision, Example: Frictional force, Viscous force, Airdrag etc., If a body is moved from position A to another position B on a rough, , 1 Joule = 10 7 erg, 1 eV = 1.6  10 19 Joule, , table, work done against frictional force shall depend on the length of the, path between A and B and not only on the position A and B., , 1 kWh = 3.6  10 6 Joule, 1 calorie = 4.18 Joule, , WAB  mgs, , (4) Mass energy equivalence : Einstein’s special theory of relativity shows that, material particle itself is a form of energy., The relation between the mass of a particle m and its equivalent, energy is given as, , Further if the body is brought back to its initial position A, work has, to be done against the frictional force, which opposes the motion. Hence the, net work done against the friction over a round trip is not zero., R, , E  mc 2 where c = velocity of light in vacuum., , s, , If m  1 amu  1.67  10 27 kg, , F, , then E  931 MeV  1.5  10 10 Joule ., , WBA  mgs., , If m  1kg then E  9  1016 Joule, , Fig. 6.14, , WNet  WAB  WBA  mgs  mgs  2mgs  0., i.e. the friction is a non-conservative force., , Examples : (i) Annihilation of matter when an electron (e  ) and a, positron (e  ) combine with each other, they annihilate or destroy each, other. The masses of electron and positron are converted into energy. This, energy is released in the form of  -rays., , Work Depends on Frame of Reference, With change of frame of reference (inertial), force does not change, while displacement may change. So the work done by a force will be, different in different frames., Examples : (1) If a porter with a suitcase on his head moves up a, staircase, work done by the, upward lifting force relative, to him will be zero (as, displacement relative to, him is zero) while relative, to a person on the ground, will be mgh., (2) If a person is, pushing a box inside a h, moving train, the work, done in the frame of train, Fig. 6.15, will, , F.s, , e  e    , Each  photon has energy = 0.51 MeV., , Here two  photons are emitted instead of one  photon to, conserve the linear momentum., (ii) Pair production : This process is the reverse of annihilation of, matter. In this case, a photon ( ) having energy equal to 1.02 MeV interacts, with a nucleus and give rise to electron (e  ) and positron (e  ) . Thus, energy is converted into matter.,  (Photon), , e– + e+, Fig.nucleus, 6.16, (iii) Nuclear bomb : When the, is split up due to mass defect, (The difference in the mass of nucleons and the nucleus), energy is released, in the form of  -radiations and heat., , while in the, , frame of earth will be F. (s  s 0 ) where s 0 is the displacement of the, train relative to the ground., , (5) Various forms of energy, (i) Mechanical energy (Kinetic and Potential), Energy, (ii) Chemical energy, The energy of a body is defined as its capacity for doing work., (iii) Electrical energy, (1) Since energy of a body is the total quantity of work done,, (iv) Magnetic energy, therefore it is a scalar quantity., (v) Nuclear energy, (2) Dimension: [ML2T 2 ] it is same as that of work or torque., (vi) Sound energy, (3) Units : Joule [S.I.], erg [C.G.S.], (vii) Light energy, Practical units : electron volt (eV), Kilowatt hour (KWh), Calories, (viii) Heat energy, (cal), (6) Transformation of energy : Conversion of energy from one form, Relation between different units:, to another is possible through various devices and processes., Table : 6.1 Various devices for energy conversion from one form to another, Mechanical  electrical, , Light  Electrical, , Chemical  electrical, , Light, N, , Dynamo, , Anode, , S, , –, , Photoelectric, , A, , cell, +, , –, , Primary, cell, , Cathode, +

Page 5 :
Work, Energy, Power and Collision 257, Chemical  heat, , Sound  Electrical, , Heat  electrical, , Fe, Hot, , Cold, , G, , Coal, Burning, , Microphone, Heat  Mechanical, , Electrical  Mechanical, , Engine, , Electrical  Heat, , Motor, Electrical  Sound, , Heater, Electrical  Chemical, , Anode, +, , Speaker, , Cu, , Thermo-couple, , Electrical  Light, , Cathode, –, , Voltameter, , Bulb, Electrolyte, , Kinetic Energy, ,  v 2  0  2as s , , The energy possessed by a body by virtue of its motion, is called, kinetic energy., Examples : (i) Flowing water possesses kinetic energy which is used, to run the water mills., (ii) Moving vehicle possesses kinetic energy., (iii) Moving air (i.e. wind) possesses kinetic energy which is used to, run wind mills., (iv) The hammer possesses kinetic energy which is used to drive the, nails in wood., (v) A bullet fired from the gun has kinetic energy and due to this, energy the bullet penetrates into a target., v, , u=0, F, , Since the displacement of the body is in the direction of the applied, force, then work done by the force is, W  F  s  ma , , Fig. 6.17, , Let, , m = mass of the body,, , u = Initial velocity of the body (= 0), , 1, 2, , This work done appears as the kinetic energy of the body, 1, KE  W  mv 2, 2, (2) Calculus method : Let a body is initially at rest and force F is, , applied on the body to displace it through small displacement d s along its, own direction then small work done, dW  F.d s  F ds, , , , dW  m a ds, , , , dW  m, , F = Force acting on the body,, a = Acceleration of the body,, s = Distance travelled by the body,, v = Final velocity of the body, From v 2  u 2  2as, , v2, 2a, ,  W  mv 2, , s, , (1) Expression for kinetic energy :, , v2, 2a, ,  dW  mdv ., , dv, ds, dt, , [As F = ma], dv , ,  As a  dt , , , , ds, dt, ,  dW  m v dv, , …(i)

Page 6 :
258 Work, Energy, Power and Collision, ds, , ,  As dt  v , , , , Therefore work done on the body in order to increase its velocity, from zero to v is given by, v, , v , 1, v, v, W  0 mv dv  m 0 v dv  m    mv 2, 2,  2  0, 2, , This work done appears as the kinetic energy of the body, 1, KE  mv 2 ., 2, In vector form KE , , 1, m (v . v ), 2, , As m and v .v are always positive, kinetic energy is always positive, scalar i.e. kinetic energy can never be negative., (3) Kinetic energy depends on frame of reference : The kinetic, energy of a person of mass m, sitting in a train moving with speed v, is zero, 1, in the frame of train but mv 2 in the frame of the earth., 2, (4) Kinetic energy according to relativity : As we know, 1, E  mv 2 ., 2, , Work done = change in kinetic energy, W  E, , This is work energy theorem, it states that work done by a force, acting on a body is equal to the change in the kinetic energy of the body., This theorem is valid for a system in presence of all types of forces, (external or internal, conservative or non-conservative)., If kinetic energy of the body increases, work is positive i.e. body, moves in the direction of the force (or field) and if kinetic energy decreases,, work will be negative and object will move opposite to the force (or field)., , Examples : (i) In case of vertical motion of body under gravity when, the body is projected up, force of gravity is opposite to motion and so, kinetic energy of the body decreases and when it falls down, force of gravity, is in the direction of motion so kinetic energy increases., (ii) When a body moves on a rough horizontal surface, as force of, friction acts opposite to motion, kinetic energy will decrease and the, decrease in kinetic energy is equal to the work done against friction., (6) Relation of kinetic energy with linear momentum: As we know, E, , 1, 1 P, mv 2    v 2, 2, 2 v , ,  E, , 1, Pv, 2, , or E , , P2, 2m, , But this formula is valid only for (v << c) If v is comparable to c, (speed of light in free space = 3  10 8 m / s ) then according to Einstein, theory of relativity, E, , mc 2, 1  (v / c ), 2, , 1, m[v 2  u 2 ], 2, ,  W, ,  mc 2, , [As P  mv ], , P, ,  As v  m , , , , So we can say that kinetic energy E , , 2, , (5) Work-energy theorem: From equation (i) dW  mv dv ., Work done on the body in order to increase its velocity from u to v, is given by, , and Momentum P , , 1, 1, p2, mv 2  Pv , 2, 2, 2m, , 2E,  2mE, v, , From above relation it is clear that a body can not have kinetic energy, without, having, momentum, and, vice-versa., , v, , v 2 , W  u mv dv  m u v dv  m  ,  2  u, v, , v, , (7) Various graphs of kinetic energy, E, , E, , E  P2, m = constant, , Ev, m = constant, 2, , v, , v, E, , E, , P, , 1, E, m, , E, , m = constant, , P = constant, P, , m, , Stopping of Vehicle by Retarding Force, If a vehicle moves with some initial velocity and due to some retarding, force it stops after covering some distance after some time., , m = Mass of vehicle,, v = Velocity, P = Momentum, E = Kinetic energy, F = Stopping force, x = Stopping distance,, t = Stopping time, (1) Stopping distance : Let

Page 7 :
Work, Energy, Power and Collision 259, Then, in this process stopping force does work on the vehicle and, destroy the motion., By the work- energy theorem, W  K , , 1, 1, mv 2, mv 2, v2, 2, 2, Stopping distance x , , , 2 g, F, ma, , 1, mv 2, 2, , [As a  g], , Initial velocity = v, , Final velocity = 0, , Stopping time t , , mv, v, mv, , , m g, g, F, , Potential Energy, Potential energy is defined only for conservative forces. In the space, occupied by conservative forces every point is associated with certain energy, which is called the energy of position or potential energy. Potential energy, generally are of three types : Elastic potential energy, Electric potential energy, and Gravitational potential energy., , x, Fig. 6.18, ,  Stopping force (F)  Distance (x) = Kinetic energy (E), Kineticenergy (E), Stopping force (F), ,  Stopping distance (x) ,  x, , mv 2, 2F, , (1) Change in potential energy : Change in potential energy between, any two points is defined in the terms of the work done by the associated, conservative force in displacing the particle between these two points, without any change in kinetic energy.,  , r, U 2  U1  r 2 F. dr  W, …(i), , …(i), , (2) Stopping time : By the impulse-momentum theorem, F  t  P  F  t  P, ,  t, , P, F, , or t , , mv, F, , 1, , …(ii), , (3) Comparison of stopping distance and time for two vehicles :, Two vehicles of masses m and m are moving with velocities v and v, respectively. When they are stopped by the same retarding force (F)., 1, , 2, , The ratio of their stopping distances, , 1, , x1, E,  1 , x2, E2, , m 1 v 12, m 2 v 22, , t, P, m v, and the ratio of their stopping time 1  1  1 1, t2, P2 m 2 v 2, , (i) If vehicles possess same velocities, v=v, 1, , 2, , x1, m,  1, x2, m2, , ;, , t1, m,  1, t2, m2, , (ii) If vehicle possess same kinetic momentum, P=P, 1, , 2, ,  P 2   2m, x1, E,  1   1   22, x 2 E2  2m1   P2, ,  m2, ,  m, 1, , , t1, P,  1 1, t2, P2, , (iii) If vehicle possess same kinetic energy, x1, E,  1 1, x2, E2, t1, P,  1 , t2 P2, , 2m1 E1, 2 m 2 E2, , Note : , , We can define a unique value of potential energy only by assigning, some arbitrary value to a fixed point called the reference point. Whenever, and wherever possible, we take the reference point at infinity and assume, potential energy to be zero there, i.e. if we take r1   and r2  r then, from equation (i),  , r, U    F. dr  W, , 2, , In case of conservative force (field) potential energy is equal to, negative of work done by conservative force in shifting the body from, reference position to given position., This is why, in shifting a particle in a conservative field (say, gravitational or electric), if the particle moves opposite to the field, work, done by the field will be negative and so change in potential energy will be, positive i.e. potential energy will increase. When the particle moves in the, direction of field, work will be positive and change in potential energy will, be negative i.e. potential energy will decrease., (2) Three dimensional formula for potential energy: For only, , , conservative fields F equals the negative gradient () of the potential, energy., , , , So F  U (  read as Del operator or Nabla operator and, ,  ˆ  ˆ  ˆ, , i, j, k), x, y, z, ,  U ˆ U ˆ U ˆ , i, j, k,  F  , y, z ,  x, where,, U,  Partial derivative of U w.r.t. x (keeping y and z constant), x, U,  Partial derivative of U w.r.t. y (keeping x and z constant), y, , , , m1, m2, , If vehicle is stopped by friction then, , U,  Partial derivative of U w.r.t. z (keeping x and y constant), z, (3) Potential energy curve : A graph plotted between the potential, energy of a particle and its displacement from the centre of force is called, potential energy curve., U(x), C, , A, , B, O, , D, , x, Fig. 6.19

Page 8 :
260 Work, Energy, Power and Collision, Figure shows a graph of potential energy function U(x) for one, dimensional motion., As we know that negative gradient of the potential energy gives, force., dU,  , F, dx, (4) Nature of force, (i) Attractive force :, On increasing x, if U increases,, dU,  positive, then F is in negative direction, dx, i.e. force is attractive in nature., In graph this is represented in region BC., (ii) Repulsive force :, On increasing x, if U decreases,, , dU,  negative , then F is in positive direction, dx, i.e. force is repulsive in nature., In graph this is represented in region AB., (iii) Zero force :, On increasing x, if U does not change,, dU,  0 then F is zero, dx, i.e. no force works on the particle., Point B, C and D represents the point of zero force or these points, can be termed as position of equilibrium., (5) Types of equilibrium : If net force acting on a particle is zero, it, is said to be in equilibrium., dU, For equilibrium,  0 , but the equilibrium of particle can be of three, dx, types :, , Stable, , Unstable, , Neutral, , When a particle is displaced slightly from its, present position, then a force acting on it, brings it back to the initial position, it is said, to be in stable equilibrium position., , When a particle is displaced slightly from its, present position, then a force acting on it tries, to displace the particle further away from the, equilibrium position, it is said to be in unstable, equilibrium., , When a particle is slightly displaced from its, position then it does not experience any force acting, on it and continues to be in equilibrium in the, displaced position, it is said to be in neutral, equilibrium., , Potential energy is minimum., , Potential energy is maximum., , Potential energy is constant., , F, , dU, 0, dx, , F, , d 2U,  positive, dx 2, , i.e. rate of change of, , dU, 0, dx, , F, , d 2U,  negative, dx 2, , dU, is positive., dx, , i.e. rate of change of, , dU, 0, dx, , d 2U, 0, dx 2, , dU, is negative., dx, , i.e. rate of change of, , dU, is zero., dx, , Example :, , Example :, , Example :, , A marble placed at the bottom of a, hemispherical bowl., , A marble balanced on top of a hemispherical, bowl., , A marble placed on horizontal table., , Elastic Potential Energy, (1) Restoring force and spring constant : When a spring is stretched or, compressed from its normal position (x = 0) by a small distance x, then a, restoring force is produced in the spring to bring it to the normal position., According to Hooke’s law this restoring force is proportional to the, displacement x and its direction is always opposite to the displacement., , i.e. F   x, or F   k x, where k is called spring constant., If x = 1, F = k (Numerically), , m, , or, x=0, F, m, +x, , F, m, , Fext, –x, Fig. 6.20, , …(i), , Fext, , k=F, , Hence spring constant is numerically equal to force required to, produce unit displacement (compression or extension) in the spring. If, required force is more, then spring is said to be more stiff and vice-versa., Actually k is a measure of the stiffness/softness of the spring., Dimension : As k , , F, x

Page 9 :
Work, Energy, Power and Collision 261,  [k ] , , [F] [MLT 2 ], ,  [MT 2 ], [x ], L, ,  Elastic potential energy U , , Units : S.I. unit Newton/metre, C.G.S unit Dyne/cm., , Note, , :, , U, , 1, Fx, 2, , F, ,  As k  x , , , , U, , F2, 2k, , F, ,  As x  k , , , , Dimension of force constant is similar to, , surface tension., (2) Expression for elastic potential energy : When a spring is, stretched or compressed from its normal position (x = 0), work has to be, done by external force against restoring force. F ext   F restoring  k x, ,  Elastic potential energy U , , Let the spring is further stretched through the distance dx, then, work done, , Note, , o, , Therefore total work done to stretch the spring through a distance x, from its mean position is given by, x2, x, x, W  0 dW  0 kx dx  k ,  2, , 1 2 1, F2, kx  Fx , 2, 2, 2k, , :, If spring is stretched from initial position, x 1 to final position x 2 then work done, =, Increment, in, elastic, potential, energy, 1,  k (x 22  x 12 ), 2,  Work done by the spring-force on the block in various, situation are shown in the following table, , dW  F ext . d x  Fext . dx cos 0  kx dx [As cos 0 = 1], o, , 1 2, kx, 2, , x, , , 1 2,   kx,  0 2, , This work done is stored as the potential energy in the stretched, spring., Table : 6.2 Work done for spring, Initial state of the spring, , Final state of the spring, , Initial position (x1), , Final position (x2), , Work done (W), , Natural, , Compressed, , 0, , –x, , –1/2 kx2, , Natural, , Elongated, , 0, , x, , –1/2 kx2, , Elongated, , Natural, , x, , 0, , 1/2 kx2, , Compressed, , Natural, , –x, , 0, , 1/2 kx2, , Elongated, , Compressed, , x, , –x, , 0, , Compressed, , Elongated, , –x, , x, , 0, , (3) Energy graph for a spring : If the mass attached with spring, performs simple harmonic motion about its mean position then its potential, energy at any position (x) can be given by, x=0, m, , This is maximum potential energy or the total energy of mass., , O, x=–a, ,  Total energy E , , m, , x=+a, , Fig. 6.21, , 1 2, kx, 2, ,  K, , B, , Now kinetic energy at any position, , …(i), , [As x =  a for extreme], E, , K, A, , O, x=0, , B, x = +a, Position, , 1, 1, k a2  k x 2, 2, 2, , 1, k (a 2  x 2 ), 2, , From the above formula we can check that, , U, , x =– a, , K  E U , K, , Energy, , 1 2, ka, 2, , 1, mv 2  0 ], 2, , m, , So for the extreme position, U, , …(ii), , [Because velocity of mass is zero at extreme position], , A, , U, , 1 2, ka, 2, , …(iii)

Page 10 :
262 Work, Energy, Power and Collision, U max , , and, , [At mean x = 0], , 1 2, ka, 2, , [At mean x = 0], , K min  0, , and, , maximum but through out the complete motion, total energy remains, constant as shown in the figure., , [At extreme x =  a], , U min  0, , K max , , E, , 1 2, ka, 2, , [At extreme x =  a], , Work Done in Pulling the Chain Against Gravity, , 1 2, ka  constant (at all positions), 2, , A chain of length L and mass M is held on a frictionless table with, (1/n) of its length hanging over the edge., th, , It means kinetic energy and potential energy changes parabolically, w.r.t. position but total energy remain always constant irrespective to, position of the mass, , Electrical Potential Energy, It is the energy associated with state of separation between charged, particles that interact via electric force. For two point charge q 1 and q 2 ,, separated by distance r., q q, U, . 1 2, 4 0, r, 1, , While for a point charge q at a point in an electric field where the, potential is V, , M,  mass per, L, unit length of the chain and y is the, length of the chain hanging over the, edge. So the mass of the chain of, length y will be ym and the force, acting on it due to gravity will be, mgy., m, , Let, , L/ n, , Fig. 6.25, , The work done in pulling the, dy length of the chain on the table., dW = F(– dy), [As y is decreasing], , i.e. dW = mgy (– dy), So the work done in pulling the hanging portion on the table., , U = qV, As charge can be positive or negative, electric potential energy can be, positive or negative., , Gravitational Potential Energy, It is the usual form of potential energy and this is the energy, associated with the state of separation, F12, F21, m1, m2, between two bodies that interact via, gravitational force., r, , For two particles of masses m and, m separated by a distance r, 1, , Fig. 6.23, , 2, , G m1m 2, Gravitational potential energy U  , r, , (1) If a body of mass m at height h relative to surface of earth then, Gravitational potential energy U , , mgh, h, 1, R, , Where R = radius of earth, g = acceleration due to gravity at the, surface of the earth., (2) If h << R then above formula reduces to U = mgh., (3) If V is the gravitational potential at a point, the potential energy, of a particle of mass m at that point will be, , U = mV, (4) Energy height graph : When a body projected vertically upward, from the ground level with some initial velocity then it possess kinetic, energy but its initial potential energy is zero., , Energy, , As the body moves upward its potential energy increases due to, increase in height but kinetic energy decreases (due to decrease in velocity)., At maximum height its kinetic energy becomes zero and potential energy, , 0, , y2 , mg L2, W , mgy dy  mg  , , L/n, 2n 2,  2  L / n, , , ,  W, , 0, , MgL, 2n 2, , [As m = M/L], , Alternative method :, If point mass m is pulled, through a height h then work, done W = mgh, Similarly for a chain we, can consider its centre of mass at, the middle point of the hanging, part i.e. at a height of L/(2n) from, the lower end and mass of the, M, hanging part of chain , n, , U, K, , Centre of mass, , Fig. 6.26, , So work done to raise the centre of mass of the chain on the table is, given by, W, , M, L, g, n, 2n, , or W , , [As W = mgh], , MgL, 2n 2, , Velocity of Chain While Leaving the Table, , ( L/ n), , L, , Fig. 6.27, , E, , L/2n

Page 11 :
Work, Energy, Power and Collision 263, Average power (Pav. ) , Taking surface of table as a reference level (zero potential energy), Potential energy of chain when 1/n length hanging from the edge,  MgL, , 2n 2, MgL, Potential energy of chain when it leaves the table  , 2, Kinetic energy of chain = loss in potential energy, 1, MgL MgL, , Mv 2 , , 2, 2, 2n 2, ,  ,  , F. d s, dW, Instantaneous power (Pinst.) , [As dW  F. ds ], , dt, dt, ,  ,  ds, [As v , ], Pinst  F. v, dt, i.e. power is equal to the scalar product of force with velocity., , th, , Important Points, (1) Dimension : [P]  [F][v]  [MLT 2 ][LT 1 ],  [P]  [ML2 T 3 ], , 1, MgL , 1 , , Mv 2 , 1 2 , 2, 2 , n , ,  Velocity of chain, , v, , 1 , , gL 1  2 , n , , , W W, , t, t, , (2) Units : Watt or Joule/sec [S.I.], , Erg/sec [C.G.S.], Practical units : Kilowatt (KW), Mega watt (MW) and Horse power, (hp), , Law of Conservation of Energy, , Relations between different units :, , (1) Law of conservation of energy, For a body or an isolated system by work-energy theorem we have,  , K 2  K 1   F. dr, …(i), , 1 W att  1 Joule / sec  10 7 erg / sec, , But according to definition of potential energy in a conservative field,  , U 2  U1   F. dr, …(ii), So from equation (i) and (ii) we have, K 2  K1  (U 2  U1 ), or K 2  U 2  K1  U1, , i.e. K + U = constant., For an isolated system or body in presence of conservative forces,, the sum of kinetic and potential energies at any point remains constant, throughout the motion. It does not depend upon time. This is known as the, law of conservation of mechanical energy., (K  U)  E  0, [As E is constant in a conservative field],  K  U  0, i.e. if the kinetic energy of the body increases its potential energy will, decrease by an equal amount and vice-versa., (2) Law of conservation of total energy : If some non-conservative, force like friction is also acting on the particle, the mechanical energy is no, more constant. It changes by the amount equal to work done by the, frictional force., (K  U)  E  W f, [where W f is the work done against friction], The lost energy is transformed into heat and the heat energy developed is, exactly equal to loss in mechanical energy., We can, therefore, write E + Q = 0, [where Q is the heat produced], This shows that if the forces are conservative and non-conservative, both, it is not the mechanical energy which is conserved, but it is the total, energy, may be heat, light, sound or mechanical etc., which is conserved., In other words : ‚Energy may be transformed from one kind to, , another but it cannot be created or destroyed. The total energy in an, isolated system remain constant". This is the law of conservation of energy., , Power, Power of a body is defined as the rate at which the body can do the, work., , 1hp  746 W att, , 1 MW  10 6 W att, , 1 KW  10 3 W att, , (3) If work done by the two bodies is same then power , , 1, time, , i.e. the body which perform the given work in lesser time possess, more power and vice-versa., (4) As power = work/time, any unit of power multiplied by a unit of, time gives unit of work (or energy) and not power, i.e. Kilowatt-hour or, watt-day are units of work or energy., 1 KW h  10 3, , J,  (60  60 sec)  3.6  10 6 Joule, sec, , (5) The slope of work time curve gives the instantaneous power. As, , P = dW/dt = tan, Work, , , , Time, Fig. 6.28, , (6) Area under power-time curve gives the work done as P ,  W , , dW, dt, ,  P dt, ,  W = Area under P-t curve, , Position and Velocity of an Automobile w.r.t Time, An automobile of mass m accelerates, starting from rest, while the, engine supplies constant power P, its position and velocity changes w.r.t, time., (1) Velocity : As Fv = P = constant, mdv , dv, , i.e. m v  P,  As F  dt , dt, , 

Page 12 :
264 Work, Energy, Power and Collision, or, , , , v dv , , , , contact while in collision of alpha particle by a nucleus (i.e. Rutherford, scattering experiment) there is no physical contact., (1) Stages of collision : There are three distinct identifiable stages in, collision, namely, before, during and after. In the before and after stage the, interaction forces are zero. Between these two stages, the interaction forces, are very large and often the dominating forces governing the motion of, bodies. The magnitude of the interacting force is often unknown, therefore,, Newton’s second law cannot be used, the law of conservation of momentum, is useful in relating the initial and final velocities., , P, dt, m, , v2, P,  t  C1, 2, m, As initially the body is at rest i.e. v = 0 at t = 0, so C1  0, , By integrating both sides we get, ,  2 Pt ,  v, ,  m , , 1/2, ,  2 Pt , (2) Position : From the above expression v  , ,  m , ds  2 Pt , or, , , dt  m , , 1/2, , F, , 1/2, , ds , ,  As v  dt , , , , m1, , Before collision, , 2,  2P , s,  . t 3 / 2  C2, 3,  m , Now as at t = 0, s = 0, so C 2  0, 1/2, , t3/2, , Collision, Collision is an isolated event in which a strong force acts between, two or more bodies for a short time as a result of which the energy and, momentum of the interacting particle change., In collision particles may or may not come in real touch e.g. in, collision between two billiard balls or a ball and bat, there is physical, , Inelastic collision, If in a collision kinetic energy after collision is, not equal to kinetic energy before collision, the, collision is said to inelastic., Coefficient of restitution 0 < e < 1, Here kinetic energy appears in other forms. In, some cases (KE) < (KE) such as when initial, KE is converted into internal energy of the, product (as heat, elastic or excitation) while in, other cases (KE) > (KE), such as when, internal energy stored in the colliding particles, is released, Examples : (1) Collision between two billiard, balls., (2) Collision between two automobile on a, road., In fact all majority of collision belong to this, category., final, , (KE) = (KE), final, , initial, , initial, , final, , Examples : (1) Collision between atomic particles, (2) Bouncing of ball with same velocity after the, collision with earth., , v1, , m2, , v2, , t, , t, During collision, , After collision, , (2) Momentum and energy conservation, in collision, Fig. 6.29, (i) Momentum conservation : In a collision, the effect of external, forces such as gravity or friction are not taken into account as due to small, duration of collision (t) average impulsive force responsible for collision is, much larger than external force acting on the system and since this, impulsive force is 'Internal' therefore the total momentum of system always, remains conserved., (ii) Energy conservation : In a collision 'total energy' is also always, conserved. Here total energy includes all forms of energy such as mechanical, energy, internal energy, excitation energy, radiant energy or even mass, energy., These laws are the fundamental laws of physics and applicable for, any type of collision but this is not true for conservation of kinetic energy., (3) Types of collision : (i) On the basis of conservation of kinetic, energy., , 1/2, , Perfectly elastic collision, If in a collision, kinetic energy after collision is equal, to kinetic energy before collision, the collision is said, to be perfectly elastic., Coefficient of restitution e = 1, , m1, , m1mm, 1 2m2, , 1/2, , , ,  8P , s, ,  9m , , u2, , m2, , Fext, ,  2 Pt , i.e. ds  ,  dt,  m , By integrating both sides we get, , , , u1, , initial, , Perfectly inelastic collision, If in a collision two bodies stick together or, move with same velocity after the collision,, the collision is said to be perfectly inelastic., Coefficient of restitution e = 0, The term 'perfectly inelastic' does not, necessarily mean that all the initial kinetic, energy is lost, it implies that the loss in, kinetic energy is as large as it can be., (Consistent with momentum conservation)., , Example : Collision between a bullet and a, block of wood into which it is fired. When, the bullet remains embedded in the block., , (ii) On the basis of the direction of colliding bodies, Head on or one dimensional collision, , Oblique collision, , In a collision if the motion of colliding particles before and after the collision, is along the same line, the collision is said to be head on or one dimensional., , If two particle collision is ‘glancing’ i.e. such that their directions of, motion after collision are not along the initial line of motion, the collision, is called oblique., If in oblique collision the particles before and after collision are in same, plane, the collision is called 2-dimensional otherwise 3-dimensional., , Impact parameter b is zero for this type of collision., , Impact parameter b lies between 0 and (r1  r2 ) i.e ., 0 < b < (r1  r2 ) where r1 and r2 are radii of colliding bodies., v1, , m1, , u1, , m2, , u2, , m1, , v1, , m2, , m1, , v2, m1, , Before collision, , u1, b, , After collision, Before collision, , m2, , , , , u2, m2, , After collision, , v

Page 13 :
Work, Energy, Power and Collision 265, , Example : collision of two gliders on an air track., , Example : Collision of billiard balls., , Perfectly elastic head on collision, , e, , v 2  v1, u1  u 2, , or, , v 2  v1  e(u1  u 2 ), , Let two bodies of masses m 1 and m 2 moving with initial velocities, u 1 and u 2 in the same direction and they collide such that after collision, , their final velocities are v 1 and v 2 respectively., u1, , m1, , u2, , m2, ,  For perfectly elastic collision, e = 1, , v1, , m1, , v2, , m2, ,  v 2  v 1  u1  u 2, ,  For perfectly inelastic collision, e = 0, , After collision, , Before collision, ,  v 2  v1  0 or v 2  v 1, , Fig. 6.30, , According to law of conservation of momentum, , It means that two body stick together and move with same velocity., , m1u1  m 2 u 2  m1v1  m 2 v 2, , … (i), ,  m1 (u1  v1 )  m 2 (v 2  u 2 ), ,  For inelastic collision, 0 < e < 1, , …(ii), ,  v 2  v1  e(u1  u 2 ), , According to law of conservation of kinetic energy, 1, 1, 1, 1, m 1 u12  m 2 u 22  m 1 v12  m 2 v 22, 2, 2, 2, 2, , , ,  v12 ) , , m 1 (u12, , m 2 (v 22, , [As shown in eq. (vi)], , In short we can say that e is the degree of elasticity of collision and, it is dimensionless quantity., , …(iii), , Further from equation (v) we get, ,  u 22 ), , …(iv), , v 2  v1  u1  u 2, , Dividing equation (iv) by equation (ii), v1  u1  v 2  u 2, , …(v), ,  u1  u 2  v 2  v1, , …(vi), , Substituting this value of, , Relative velocity of separation is equal to relative velocity of, approach., , Note, , :  The ratio of relative velocity of separation and, , relative velocity of approach is defined as coefficient of restitution., , v 2 in equation (i) and rearranging, ,  m  m2 , 2m 2 u 2,  u1 , we get, v1   1, , m, , m, m, 2 , 1  m2,  1, , Similarly we get,,  m  m1 , 2m1u1,  u2 , v 2   2, , m, , m, m, 2 , 1  m2,  1, , (1) Special cases of head on elastic collision, (i) If projectile and target are of same mass i.e. m = m, 1, ,  m  m2, Since v1   1,  m1  m 2, , 2, , , 2m 2,  u1 , u2, , m, 1  m2, , ,  m  m1 , 2m1u1,  u2 , v 2   2, , m, , m, m, 2 , 1  m2,  1, , and, , Substituting m1  m 2 we get, v1  u2, , and, , v 2  u1, , It means when two bodies of equal masses undergo head on elastic collision, their velocities get interchanged., Example : Collision of two billiard balls, Before collision, 10 kg, , u1 = 50m/s, , After collision, , 10 kg, , 10 kg, , 10 kg, , u2 = 20m/s, , v1 = 20 m/s, , v2 = 50 m/s, , (ii) If massive projectile collides with a light target i.e. m >> m, 1, , 2, , …(vii), , Sub case : u2  0 i.e. target is at rest, v1  0 and v 2  u1, , …(viii)

Page 14 :
266 Work, Energy, Power and Collision,  m  m2, Since v1   1,  m1  m 2, , , 2m 2u 2,  u1 , , m, 1  m2, , ,  m  m1 , 2m1u1,  u2 , v 2   2, , m, , m, m, 2 , 1  m2,  1, , and, , Substituting m 2  0 , we get, v1  u1 and v 2  2u1  u2, , Example : Collision of a truck with a cyclist, u1 = 120 km/hr, m1 = 103 kg, , m2 = 60 kg, u2 = 10 km/hr, , Before collision, v1 = 120 km/hr, , Sub case : u 2  0 i.e. target is at rest, , v2 = 230 km/hr, , v = u and v = 2u, , After collision, , 1, , 1, , 2, , 1, , (iii) If light projectile collides with a very heavy target i.e. m << m, 1, ,  m  m2 , 2m 2 u 2,  u1 , Since v1   1, , m, , m, m, 2 , 1  m2,  1, Substituting m1  0 , we get, , 2, ,  m  m1 , 2m1u1,  u2 , v 2   2, , m, , m, m, 2 , 1  m2,  1, , and, , v1   u1  2u2 and v 2  u2, , Example : Collision of a ball with a massive wall., Sub case : u 2  0 i.e. target is at rest, v2 = 2 m/s, , u2 = 2 m/ s, u1 = 30 m/s, , v = – u and v = 0, i.e. the ball rebounds with same speed in opposite, 1, , v1 = – 26 m/s, , 1, , 2, , direction when it collide with stationary and very massive, wall., , m1 = 50gm, m2 = 100 kg, Before collision, , After collision, , (2) Kinetic energy transfer during head on elastic collision, 1, Kinetic energy of projectile before collision Ki  m1u12, 2, , Kinetic energy of projectile after collision K f , ,  m  m2 , 2m 2 u 2,  u1 , v 1   1, , m, , m, m, 1, 2, 1  m2, , ,  m  m2 ,  u1, If the target is at rest i.e. u = 0 then v1   1, ,  m1  m 2 , , 1, m 1 v 12, 2, , 2, , Kinetic energy transferred from projectile to target K = decrease in, kinetic energy in projectile, 1, 1, 1, K  m 1 u 12  m 1 v 12  m 1 (u12  v 12 ), 2, 2, 2, , From equation (i), , or, , 4m1m 2, K, , K, (m 1  m 2 ) 2, , or, , 4m1m 2, K, , K, (m 1  m 2 ) 2  4 m 1 m 2, , Fractional decrease in kinetic energy, 1, m (u 2  v 12 ), v, K 2 1 1,  1   1, , 1, K,  u1, m 1 u 12, 2, , , , , , , 2, , We can substitute the value of v1 from the equation, , …(i), ,  m  m2 , K, ,  1   1, , K,  m1  m 2 , , Note, , :, , 2, , …(ii), , …(iii), , , , …(iv), , Greater the difference in masses,, , lesser will be transfer of kinetic energy and vice versa

Page 15 :
Work, Energy, Power and Collision 267,  Transfer of kinetic energy will be maximum when the, difference in masses is minimum, m1  m 2  0, , i.e., , m 1  m 2 then, , or, , K,  1  100%, K, , , , So the transfer of kinetic energy in head on elastic collision, (when target is at rest) is maximum when the masses of particles are equal, i.e. mass ratio is 1 and the transfer of kinetic energy is 100%., , ,  v2 , , 2u 1, As u 2  0 and, 1  m 2 / m1, , Assuming, , If m 2  n m 1 then from equation (iii) we get, , K, 4n, , K, (1  n)2, ,  v2 , , , Kinetic, , energy, , retained, , by, , the, , projectile, ,  K ,  1  kinetic energy transferred by projectile, , ,  K Retained, 2, ,  m m ,  m  m2 ,  K , 2, ,    1,  ,  1  1   1, , m m , , K, m, , m, , , , Retained, 1, 2 , 1, 2 , , , , , , 2m 1 u 1, m1  m 2, , m2, n, m1, , 2u 1, 1n, , (ii) Momentum of target : P2  m 2 v 2 , , 2u 1 , ,  As m 2  m 1 n and v 2  1  n , , , , 2, ,  P2 , , (3) Velocity, momentum and kinetic energy of stationary target after head on, elastic collision, , 2m 1 u 1, 1  (1 / n), , (iii) Kinetic energy of target :, , (i) Velocity of target : We know, , 2, ,  m  m1 , 2m 1 u 1, u2 , v 2   2, , m, , m, m, 2 , 1  m2,  1, , u1, , m1, , m2, , 2nm 1 u 1, 1n, , u2=0, , v1, , m1, , Before collision, , m2, , v2, , K2 , , 2 m 1 u 12 n,  2u , 1, 1, m 2 v 22  n m 1  1  , 2, 2, (1  n) 2, 1  n , , , , 4 (K 1 )n, (1  n)  4 n, 2, , 1, , 2,  As K 1  2 m 1 u 1 , , , , (iv) Relation between masses for maximum velocity, momentum and, kinetic energy, , After collision, Fig. 6.31, , Velocity, , For v 2 to be maximum n must be minimum, 2u1, v2 , 1n, , i.e., , Momentum, P2 , , m2,  0  m 2  m1, m1, , For P2 to be maximum, (1/n) must be minimum or n must be, maximum., , 2m1u1, (1  1 / n), , i.e., , Kinetic energy, K2 , , n, , n, , i.e., , Target should be massive., , m2,    m 2  m1, m1, , For K 2 to be maximum (1  n)2 must be minimum., , 4 K1 n, (1  n)2  4 n, , Target should be very light., , m, 1  n  0  n  1  2  m 2  m1, m1, , Target and projectile should, be of equal mass., , Perfectly Elastic Oblique Collision, Let two bodies moving as shown in figure., By law of conservation of momentum, v1, , Along x-axis, m 1u1  m 2 u 2  m 1v1 cos   m 2 v 2 cos , , m1, m1, , u1, m2, , , , , Before collision, , u2, m2, , Fig. 6.32, , Along y-axis, 0  m 1 v1 sin  m 2 v 2 sin, , After collision, , v2, , ...(ii), , ...(i)

Page 16 :
268 Work, Energy, Power and Collision, By law of conservation of kinetic energy, ,  e, , 1, 1, 1, 1, m 1 u 12  m 2 u 22  m 1 v 12  m 2 v 22, 2, 2, 2, 2, , ...(iii), , In case of oblique collision it becomes difficult to solve problem, unless some experimental data is provided, as in these situations more, unknown variables are involved than equations formed., , u1  v 1 cos   v 2 cos , , ...(iv), , 0  v 1 sin  v 2 sin, , and, , …(i), , By conservation of momentum :, Momentum before collision = Momentum after collision, ,  v1  v 2  u, , values in equation (i), (ii) and (iii) we get, ,  v 12, , v 2  v 1  eu, , mu  mv 1  mv 2, , Special condition : If m 1  m 2 and u 2  0 substituting these, , u12, , , , v 2  v1 v 2  v1, , u1  u 2, u0, , …(ii), , Solving equation (i) and (ii) we get v 1 , , ...(v), ,  v 22, , …(vi), , and v 2 , , , Squaring (iv) and (v) and adding we get, u12  v 12  v 22  2v 1 v 2 cos(   ), , …(vii), , u, (1  e ), 2, , u, (1  e ), 2, , v1 1  e, , v2 1  e, , (3) Loss in kinetic energy, , Using (vi) and (vii) we get cos(   )  0, , Loss in K.E. (K) = Total initial kinetic energy, – Total final kinetic energy, ,     / 2, , i.e. after perfectly elastic oblique collision of two bodies of equal masses (if, the second body is at rest), the scattering angle    would be 90 o ., , 1, 1, 1,  1, , =  m 1 u 12  m 2 u 22    m 1 v 12  m 2 v 22 , 2, 2, 2, 2, ,  , , , Head on Inelastic Collision, , Substituting the value of v1 and v 2 from the above expressions, , (1) Velocity after collision : Let two bodies A and B collide, inelastically and coefficient of restitution is e., , Loss (K) =, , Where, e, , By substituting e = 1 we get K = 0 i.e. for perfectly elastic collision,, loss of kinetic energy will be zero or kinetic energy remains same before, and after the collision., , v 2  v 1 Relativevelocityof separation, , u1  u 2, Relativevelocityof approach, ,  v 2  v1  e(u1  u 2 ), , Rebounding of Ball After Collision With Ground, ,  v 2  v1  e(u1  u 2 ), , …(i), , If a ball is dropped from a height h on a horizontal floor, then it, strikes with the floor with a speed., , From the law of conservation of linear momentum, m 1 u1  m 2 u 2  m 1 v 1  m 2 v 2, , and it rebounds from the floor with a speed, , ,  (1  e ) m 2,  u1  , ,  m m, 2, ,  1, , , u2, , , , h0, ,  (1  e ) m 1 ,  m 2  e m1, Similarly v 2  ,  u 1  , m, , m, 1, 2, , ,  m1  m 2, , u2 = 0, m, , t0, , v1, m, , Before collision, , v2, m, , After collision, , h2, v1, , v0, , (2) Ratio of velocities after inelastic collision : A sphere of mass m, moving with velocity u hits inelastically with another stationary sphere of, same mass., u1 = u, , h1, , , u2, , , , By substituting e = 1, we get the value of v1 and v 2 for perfectly, elastic head on collision., , m, , [From v 2  u 2  2 gh], , v 0  2gh0, , …(ii), , By solving (i) and (ii) we get,  m  em 2, v 1   1,  m1  m 2, , 1  m1m 2 , ,  (1  e 2 ) (u1  u2 )2, 2  m1  m 2 , , v2, t2, , t1, Fig. 6.34, , v 1  e v 0  e 2gh0, , , velocityafter collision ,  Ase , , velocity, before collision, , , (1) First height of rebound : h1 , , , h = eh, 2, , 1, , 0, , (2) Height of the ball after n rebound : Obviously, the velocity of, ball after n rebound will be, th, , Fig. 6.33, , v 12,  e 2 h0, 2g, , th

Page 17 :
Work, Energy, Power and Collision 269, m 1u1  m 2 (u 2 )  (m 1  m 2 )v comb, , vn  e nv0, , (Taking left to right as positive), , Therefore the height after n rebound will be, th, , hn , , v n2, 2g, ,  v comb , ,  e 2n h0, , m 1 u1  m 2 u 2, m1  m 2, ,  hn  e 2 n h 0, (3) Total distance travelled by the ball before it stops bouncing, H  h0  2h1  2h2  2h3  ...  h0  2e 2h0  2e 4 h0  2e 6 h0  ..., 2, , 4, , ,  1,  h0 1  2e 2 , 1  e2, , , when m 1 u1  m 2 u 2 then v comb  0 (positive), , , , , , i.e. the combined body will move along the direction of motion of, , 2h0, g, , [1  2e  2e 2  ......], , , , 2h 0, g, , [1  2e (1  e  e 2  e 3  ......)], , , , 2h 0, g, , ,  1 ,  , 1  2e ,  1  e , , , when m 1 u1  m 2 u 2 then v comb  0 (negative), , (3) Loss in kinetic energy, , 2h0, 2h1, 2h2, 2, 2,  .., g, g, g, , T  t0  2t1  2t2  2t3  .. , , mass m 1 ., , i.e. the combined body will move in a direction opposite to the, motion of mass m 1 ., , 1  e 2 ,  H  h0 , 2 ,  1  e , (4) Total time taken by the ball to stop bouncing, , [As h1  e 2 h0 ; h 2  e 4 h0 ], , K = Initial kinetic energy – Final kinetic energy, 1, 1,  1, , 2,   m 1 u 12  m 2 u 22    (m 1  m 2 ) v comb, , 2, 2,  2, , , , 1 m 1m 2, (u1  u 2 )2, 2 m1  m 2, , Collision Between, Suspended Block, , 2h 0  1  e , , , g 1  e , , In such types of collisions, the bodies move independently before, collision but after collision as a one single body., (1) When the colliding bodies are moving in the same direction, By the law of conservation of momentum, , m1, , Let v be the velocity of the system (block + bullet) just after the, collision., L–h , , m 1 u1  m 2 u 2, m1  m 2, m2, , Vertically, , (1) Velocity of system, , m 1 u1  m 2 u 2  (m 1  m 2 )v comb, , u2, , and, , After the collision bullet gets embedded in block. Let the combined, system raised upto height h and the string makes an angle  with the, vertical., , Perfectly Inelastic Collision, , u1, , Bullet, , A bullet of mass m is fired horizontally with velocity u in block of, mass M suspended by vertical thread., ,  1  e  2h 0,  T , , g, 1  e , ,  v comb , , m2, , Before collision, , 6, , 1 , , 2, 4,  As 1  e  e  .... , , 1e2 , , , , , u2, , Fig. 3.36, , H  h0 [1  2e (1  e  e  e ....)], 2, , u1, , m1, , m, , M, u, , vcomb, m1, , L, , m2, , h, , M, Fig. 3.37, , Momentum + Momentum = Momentum, bullet, , Before collision, , After collision, , Loss in kinetic energy, 1, 1,  1, 2, K   m 1 u 12  m 2 u 22   (m 1  m 2 )v comb, 2, 2,  2, ,  v, , 1  m1m 2, , 2  m 1  m 2, , ,  (u 1  u 2 ) 2, , , [By substituting the value of v ], (2) When the colliding bodies are moving in the opposite direction, comb, , By the law of conservation of momentum, , bullet and block system, , mu  0  (m  M )v, , Fig. 6.35, , K , , block, , mu, (m  M ), , …(i), , (2) Velocity of bullet : Due to energy which remains in the bulletblock system, just after the collision, the system (bullet + block) rises upto, height h., By, the, conservation, of, 1, (m  M )v 2  (m  M )gh  v  2 gh, 2, , mechanical, , energy

Page 18 :
270 Work, Energy, Power and Collision, Now substituting this value in the equation (i) we get, mu, 2 gh , mM, , done., ,  When work is done on a body, its kinetic or potential energy, increases., ,  When the work is done by the body, its potential or kinetic energy, ,  (m  M ) 2 gh ,  u, , m, , , , decreases., ,  According to the work energy theorem, the work done is equal to, , (3) Loss in kinetic energy : We know that the formula for loss of, kinetic energy in perfectly inelastic collision, , the change in energy. That is W  E ., , 1 m1m 2, K , (u1  u2 )2, 2 m1  m 2, same direction.), , minimum stopping force or minimum stopping distance. If a body is, brought to a halt, the work done to do so is equal to the kinetic energy, lost., ,  K , , (When the bodies are moving in, ,  Potential energy of a system increases when a conservative force, , 1 mM, u2, 2 mM, , does work on it., ,  The kinetic energy of a body is always positive.,  When the momentum of a body increases by a factor n, then its, , [As u1  u , u 2  0 , m 1  m and m 2  M ], , kinetic energy is increased by factor n ., 2, , (4) Angle of string from the vertical,  (m  M ) 2 gh , From the expression of velocity of bullet u  ,  we, m, , , , can get h , , u  m , , , 2g  m  M , 2, , or, ,  If the speed of a vehicle is made n times, then its stopping distance, becomes n times., 2, ,  The total energy (including mass energy) of the universe remains, constant., , 2, , From the figure cos  , ,  Work energy theorem is particularly useful in calculation of, ,  One form of energy can be changed into other form according to, u  m , Lh, h, 1  1, , , 2 gL  m  M , L, L, 2, , 2, , 2, , 1  mu  ,   cos 1 1 , ,  , 2 gL  m  M  , , , the law of conservation of energy. That is amount of energy lost of one, form should be equal to energy or energies produced of other forms., ,  Kinetic energy can change into potential energy and vice versa., When a body falls, potential energy is converted into kinetic energy., ,  Pendulum oscillates due to conversion of kinetic energy into, potential energy and vice versa. Same is true for the oscillations of mass, attached to the spring., ,  Conservation laws can be used to describe the behaviour of a, mechanical system even when the exact nature of the forces involved is, not known., ,  Although the exact nature of the nuclear forces is not known, yet,  The area under the force-displacement graph is equal to the work, done., ,  Work done by gravitation or electric force does not depend on the, path followed. It depends on the initial and final positions of the body., Such forces are called conservative. When a body returns to the starting, point under the action of conservative force, the net work done is zero, that is, ,  Work done against friction depends on the path followed. Viscosity, and friction are not conservative forces. For non conservative forces, the, , , , , , ,  Violation of the laws of conservation indicates that the event cannot, take place., ,  The gravitational potential energy of a mass m at a height h above, the surface of the earth (radius R) is given by U , , mgh, . When h <<, 1  h/R, , R, we find U=mgh., ,  dW  0 ., , work done on a closed path is not zero. That is, , we can solve problems regarding the nuclear forces with the help of the, conservation laws., ,  dW  0 ., , Work done is path independent only for a conservative field., Work done depends on the frame of reference., Work done by a centripetal force is always zero., , Energy is a promise of work to be done in future. It is the stored, ability to do work., ,  Energy of a body is equal to the work done by the body and it has, nothing to do with the time taken to perform the work. On the other, hand, the power of the body depends on the time in which the work is, , 1, 2, ,  Electrostatic energy in capacitor - U  CV 2 , where C is, capacitance, V = potential difference between the plates., ,  Electric potential energy of a test charge q at a place where electric, 0, , potential is V, is given by : U =q V., P, , 0, ,  Electric potential energy between two charges (q and q ) separated, 1, , 2, , 1 q1q 2, by a distance r is given by U , . Here  0 is permittivity of, 4 0 r, 9, 2 2, vacuum and 1 / 4  0  9  10 Nm C ., ,  Magnetic energy stored in an inductor –, U, , 1 2, LI , where L = inductance, I = current., 2

Page 19 :
Work, Energy, Power and Collision 271, ,  Energy gained by a body of mass m, specific heat C, when its, temperature changes by  is given by : Q  mC  ., ,  The Potential energy associated with a spring of constant k when, extended or compressed by distance x is given by U , , 1 2, kx ., 2, , , , , , , , , , where u1 and u 2 are initial velocities and v1 and v 2 are the velocities, of the colliding bodies after the collision. This is called Newton's law of, impact., ,  The collision is said to be inelastic when the kinetic energy is not, conserved., ,  Kinetic energy of a particle executing SHM is given by :, 1, K  m  2 (a 2  y 2 ) where m = mass,  = angular frequency, a=, 2, amplitude, y = displacement., ,  In the perfectly inelastic collision, the colliding bodies stick, together. That is the relative velocity of the bodies after the collision is, zero., ,  In an elastic collision of two equal masses, their kinetic energies are, exchanged., ,  Potential energy of a particle executing SHM is given by :, ,  If a body of mass m moving with velocity v, collides elastically with, , 1, U  m 2 y 2 ., 2, , a rigid wall, then the change in the momentum of the body is 2mv., ,  Total energy of a particle executing SHM is given by :, E  K U , , 1, m  2a2 ., 2, ,  Energy density associated with a wave , ,  , v 2  v1,  e    is called coefficient of restitution. Its value is 1 for, u1  u 2, elastic collisions. It is less than 1 for inelastic collisions and zero for, perfectly inelastic collision., , 1,  2 a 2 where, 2, ,  =density of medium,  = angular frequency, a = amplitude of the of, the wave., , , , , , , During collision, velocity of the colliding bodies changes., Linear momentum is conserved in all types of collisions., Perfectly elastic collision is a rare physical phenomenon., , Collisions between two ivory or steel or glass balls are nearly, elastic., ,  Energy associated with a photon :, E  h  hc /  , where h = planck’s constant,  = frequency of the, light wave, c = velocity of light,  = wave length., ,  The force of interaction in an inelastic collision is non-conservative, in nature., ,  Mass and energy are interconvertible. That is mass can be, ,  In inelastic collision, the kinetic energy is converted into heat, , converted into energy and energy can be converted into mass., , energy, sound energy, light energy etc., ,  A mass m (in kg) is equivalent to energy (in J) which is equal to, ,  In head on collisions, the colliding bodies move along the same, , mc where c = speed of light., , straight line before and after collision., ,  A stout spring has a large value of force constant, while for a, ,  Head on collisions are also called one dimensional collisions.,  In the oblique collisions the colliding bodies move at certain angles, , 2, , delicate spring, the value of spring constant is low., ,  The term energy is different from power. Whereas energy refers to, the capacity to perform the work, power determines the rate of, performing the work. Thus, in determining power, time taken to perform, the work is significant but it is of no importance for measuring energy, of a body., ,  Collision is the phenomenon in which two bodies exert mutual, force on each other., ,  The collision generally occurs for very small interval of time.,  Physical contact between the colliding bodies is not essential for the, , before and/or after the collisions., ,  The oblique collisions are two dimensional collisions.,  When a heavy body collides head-on elastically with a lighter body,, then the lighter body begins to move with a velocity nearly double the, velocity of the heavier body., ,  When a light body collides with a heavy body, the lighter body, returns almost with the same speed., ,  If a light and a heavy body have equal momenta, then lighter body, , collision., , has greater kinetic energy., ,  The mutual forces between the colliding bodies are action and, ,  Suppose, a body is dropped form a height h and it strikes the, , reaction pair. In accordance with the Newton’s third law of motion, they, are equal and opposite to each other., , ground with velocity v . After the (inelastic) collision let it rise to a, height h . If v be the velocity with which the body rebounds, then, , 0, , 0, , 1, ,  The collision is said to be elastic when the kinetic energy is, , 1, , v1  2 gh1 , , , v0  2 gh0 , , 1/2, , h ,  1,  h0 , , 1/2, , conserved., , e, ,  In the elastic collisions the forces involved are conservative.,  In the elastic collisions, the kinetic or mechanical energy is not, ,  If after n collisions with the ground, the velocity is v and the height, n, , converted into any other form of energy., , to which it rises be h , then, ,  Elastic collisions produce no sound or heat.,  There is no difference between the elastic and perfectly elastic, , en , , n, , collisions., ,  In the elastic collisions, the relative velocity before collision is equal, , , , , , , , , to the relative velocity after the collision. That is u1  u 2  v 2  v1, , vn  hn ,  , v0  h0 , , 1/2, ,  , , , ,  P  F . v  F v cos  where v is the velocity of the body and, , ,  is the angle between F and v .

Page 20 :
272 Work, Energy, Power and Collision,  Area under the F  v graph is equal to the power dissipated.,  Power dissipated by a conservative force (gravitation, electric force, etc.) does not depend on the path followed. It depends on the initial and, final positions of the body. That is, , , , dP  0 ., ,  Power dissipated against friction depends on the path followed., That is, , , , dP  0 ., ,  Power is also measured in horse power (hp). It is the fps unit of, power. 1 hp = 746 W., ,  An engine pulls a train of mass m with constant velocity. If the rails, are on a plane surface and there is no friction, the power dissipated by, the engine is zero., ,  In the above case if the coefficient of friction for the rail is  , the, power of the engine is P   mgv ., ,  In the above case if the engine pulls on a smooth track on an, inclined plane (inclination  ), then its power P  (mg sin ) v ., ,  In the above case if the engine pulls upwards on a rough inclined, plane having coefficient of friction  , then power of the engine is, , P  ( cos   sin )mg v ., ,  If the engine pulls down on the inclined plane then power of the, engine is, , P  ( cos   sin )mg v .