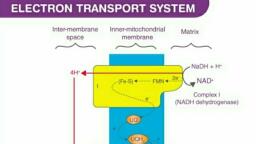
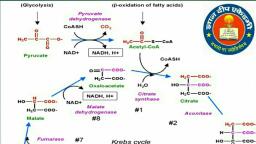
Page 1 :
Particle Kinematics, , Kinematics, , In kinematics we study how a body moves without knowing why it moves. All particles of a rigid body in, translation motion move in identical fashion hence any of the particles of a rigid body in translation motion can, be used to represent translation motion of the body. This is why, while analyzing its translation motion, a rigid, body is considered a particle and kinematics of translation motion as particle kinematics., , Particle kinematics deals with nature of motion i.e. how fast and on what path an object moves and relates the, position, velocity, acceleration, and time without any reference to mass, force and energy. In other words, it is, , study of geometry of motion., , Types of Translation Motion, , A body in translation motion can move on either a straight-line path or curvilinear path., , Rectilinear Motion, , Translation motion on straight-line path is known as rectilinear translation. It is also known as one-dimensional, motion. A car running on a straight road, train running on a straight track and a ball thrown vertically upwards, , or dropped from a height etc are very common examples of rectilinear translation., , Curvilinear Motion, , Translation motion of a body on curvilinear path is/known»as\curvilinear translation. If the trajectory is in a, plane, the motion is known as two-dimensional, motion. A ball.thrown at some angle with the horizontal describes, a curvilinear trajectory in a vertical plane; a stone tied 'to’a string when whirled describes a circular path and an, insect crawling on thesfloor or”6n a wall are.examples of two-dimensional motion., , If path is not in a plane*and requires a region of space or volume, the motion is known as three-dimensional, motion or motion is space. An insect flying randomly in a room, motion of a football in soccer game over, considerable duration of time etc are common examples of three-dimensional motion., , Translation Motion, , «Ho —_,, , Rectilinear Motion Curvilinear Motion, Or, One Dimensional Motion ot, Motion ina Plane Motion in Space, Or Or, Two Dimensional Motion Three Dimensional Motion, , Reference Frame, , Motion of a body can only be observed if it changes its position with respect to some other body. Therefore, for, a motion to be observed there must be a body, which is changing its position with respect to other body and a, person who is observing motion. The person observing motion is known as observer. The observer for the, purpose of investigation must have its own clock to measure time and a point in the space attached with the, other body as origin and a set of coordinate axes. These two things the time measured by the clock and the, coordinate system are collectively known as reference frame., , In this way, motion of the moving body is expressed in terms of its position coordinates changing with time.

Page 2 :
Position Vector, Velocity and Acceleration Vector, For analyzing translation motion, we assume the moving body as a particle and represent it as mathematical, point. Consider a particle P moving on a curvilinear path., , Position-Vector, , It describes position of a particle relative to other particle and is a vector from the later towards the first. To, study motion of a particle we have to assume a reference frame fixed with some other body. The vector drawn, from the origin of the coordinate system representing the reference frame to the location of the particle P is, , known as position vector of the particle P., , Consider a particle P moving in space traces a path shown In the figure. Its position continuously changes with, , time and so does the position vector. At an instant of time, its position vector 7 is shown in the following figure., , , , Position Vector Displacement Vector & Distance Traveled, , Displacement and distance traveled, , Displacement is measure of change in place i.e. position of particle. It is defined by a vector from the initial, position to the final position. Let the particle.moves from point A to B on the curvilinear path. The vector, AB = Ar is displacement., , Distance traveled. is length of the path traversed. We can say it “path length”. Here in the figure length of the, curve As from A to B is the distance traveled., , Distance traveled between two ‘places is greater than the magnitude of displacement vector wherever particle, changes its direction during its motion. In unidirectional motion, both of them are equal., , Average Velocity and Average Speed Yb By, , Average velocity of a particle in a time interval is that constant velocity with, which particle would have covered the same displacement in the same time =, interval as it covers in its actual motion. It is defined as the ratio of displacement ", , to the concerned time interval. AW, If the particle moves from point A to point B in time interval t, to t,, the 6 [A], x, , average velocity ¥,, in this time interval is given by the following equation. =, , As, , , , _ _AF_a-i, vee, At t,-t,, , Similar to average velocity, average speed in a time interval is that constant speed with which particle would |, travel the same distance on the same path in the same time interval as it travels in its actual motion. It is defined , as the ratio of distance traveled to the concerned time interval., , If in moving from point A to B, the particle travels path length i.e. distance As in time interval t to t, its average, speed c, is given by the following equation. ; ', , Path Length, , As, c.=—=, At t,-t, ', , av

Page 3 :
Average speed in a time interval is greater than the magnitude of average velocity vector wherever particle, changes its direction during its motion. In unidirectional motion, both of them are equal., , Instantaneous Velocity and speed, , If we assume the time interval At to be infinitesimally small i.e. At -» 0, the point B approaches A making the, chord AB to coincide with the tangent at A. Now we can express the instantaneous velocity % by the following, equations., , , , The instantaneous velocity equals to the rate of change in its position vector 7 with time. Its direction is along, the tangent to the path. Instantaneous speed is defined as the time rate of distance traveled., , x0 At dt, , You can easily conceive that when At->0, not only the chord AB but also the arc AB both approach to, , coincide with each other and with the tangent. Thereforesds =|dr|:, Now.we can say that speed equals to, magnitude of instantaneous velocity., , Instantaneous speed tells us how fast a particle moves at an instant and instantaneous velocity tells us in what, direction and with what speed a particle moves at.an instant of time., , Acceleration, , Instantaneous acceleration 4 is measure of how fast velocity of a body changes i.e. how fast direction of motion, and speed change with time., , At an instant, it equals to the rate of change in velocity vector ¢ with time., , qv, dt, , , , A vector quantity changes, when its magnitude or direction or both change. Accordingly, acceleration vector, , may have two components, one responsible to change only speed and the other responsible to change only, direction of motion.

Page 4 :
Component of acceleration responsible to change speed must be in the direction of motion. It is known as, , tangential component of acceleration a,. The component responsible to change direction of motion must be, , perpendicular to the direction of motion. It is known as normal component of acceleration a,. Acceleration, , vector 4 of a particle moving on a curvilinear path and its tangential and Normal components are shown in the, figure., , Curvilinear Translation in Cartesian coordinate system:, , Superposition of three rectilinear Motions, Consider a particle moving on a three dimensional curvilinear path AB. At an instant of time t it is at point P, , (x, y, z) moving with velocity G and acceleration . Its position vector is defined by equations, F=xi+yj+zk, Differentiating it with respect to time, we get velocity vector., , __dr_dx- dy. dz- os ee, We et al ant eee teed tye, Here v, =dx/dt, v, =dy/dt and v, =dz/dt are the components, , of velocity vectors in the x, y and z- directions respectively., Now the acceleration can be obtained by differentiating velocity, vector ¥ with respect to time., , , , dv... dv dv, —j4—2j 4 —, at it j+Sek= a,i+a,j+ak, , Acceleration vector can also be obtained by differentiating position vector twice with respect to time., ar d’x= od’x' d’xe, , a-ak at ae j+ Be <r ke a,itajjt+a,k, , In the above two equations, a, = d?x/dt? =dv, /dt, a, =d’y/dt® =dv, /dt and a, = d?z/dt? = dv, /dt are the, components of acceleration vectors in the x, y and z- directions respectively., , In the above equations, we can analyze each of the components x, y and z of motion as three individual, rectilinear motions each along one of the axes x, y and z., , dx dv,, , Along the x-axis v= a and a= ra, dy dv, , Along the y-axis v= at and a= 7, dz dv, , — =— =, , Along the z-axis irr and =, , A curvilinear motion can be analyzed as superposition of three simultaneous rectilinear motions each along one, of the coordinate axes., , Example, , Position vector 7 of a particle varies with time t according to the law r= (3t*)i-(4'*)]+(2t)k, where r is in, meters and t is in seconds., , (a) Find suitable expression for its velocity and acceleration as function of time., , (b) Find magnitude of its displacement and distance traveled in the time interval t = 0 to 4s.

Page 5 :
Solution, , (a) Velocity % is defined as the first derivative of position vector with respect to time., , ¥=S=ti-2Vtj+2k m/s, , Acceleration @ is defined as the first derivative of velocity vector with respect to time., , Magnitude of displacement Ar = /8? +, , , , Distance As is defined as the path length and can be calculated by integrating speed over the concerned time, interval., , As = [v= [ve +4t+4dt= [tv+2}a= 16m, , Rectilinear Motion, , Curvilinear motion can be conceived as superposition,of three rectilinear motions each along one of the, Cartesian axes. Therefore, we first study rectilinear’motion,in detail., , We can classify rectilinear motion problems in following Categories according to given information., , , , Rectilinear Motion, Me, Uniform Velocity Accelerated Motion, Motion 1, Uniform Accderation Variable Acceleration Motion, Motion Acceleration as function of time., IL Acceleration as function of position., , Il. Accderation as function of velocity., , , , , , , , Uniform Velocity Motion, , In uniform velocity motion, a body moves with constant speed on a straight-line path without change in direction., If a body starting from position x = x, at the instant t = 0, moves with uniform velocity v in the positive xdirection, its equation of motion at any time t is x =x, + vt, , {Velocity, , v, , Velocity-time (v-t) graph for this motion is shown in the following figure., , , , > Time, , Velocity-time graph