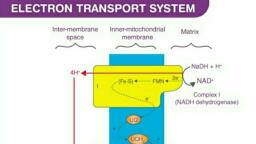
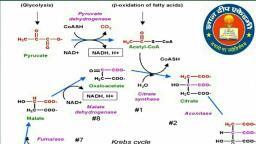
Page 1 :
1., , 2., , VE R, , SCALAR:, In physics we deal with two type of physical quantity one is scalar and other is vector. Each scalar, quantity has a magnitude and a unit., Forexamplemass =4kg, Magnitudeofmass =4, and unit of mass =kg, Example of scalar quantities : mass, speed, distance etc., Scalar quantities can be added, subtracted and multiplied by simple laws of algebra., VECTOR :, , Vector are the physical quantites having magnitude as well as specified direction., , For example :, , Speed = 4 m/s (isa scalar), Velocity = 4 m/s toward north (is a vector), , If someone wants to reach some location then it is not sufficient to provide information about the, distance of that location it is also essential to tell him about the proper*direction from the initial, location to the destination., , The magnitude of a vector (4 ) is the absolute value of.a vector and Is indicated by |A| or A., , Example of vector quantity : Displacement, vel6city, acceleration, force etc., , Knowledge of direction ‘i, w E, Ss, 3. GENERAL POINTS REGARDING VECTORS :, , 3.1, , Representation of vector :, , Geometrically, the vector is represented by a line with an arrow indicating the direction of vector as, Tail———___—_—>, = —— Length Head, (magnitude), Mathematically, vector is represented by 4., , Sometimes it is represented by bold letter A., , Thus, the arrow in abow figure represents a vector A, in xy-plane making an angle 6 with x-axis,, , , , A representation of vector will be complete if it gives us direction and magnitude.

Page 2 :
3.2, , Ex.1, , 3.3, , Symbolic form : ¥,a,F,s used to separate a vector quantity from scalar quantities (u, i, m), Graphical form : A vector is represented by a directed straight line,, having the magnitude and direction of the quantity represented by it., e.g. if we want to represent a force of 5 N acting 45° N of E, , (i) We choose direction co-ordinates., , (ii) We choose a convenient scale like 1 cm=1N, , (iii) We draw a line of length equal in magnitude and in the direction, of vector to the chosen quantity., , (iv) We put arrow in the direction of vector., , , , AB, Magnitude of vector :, , | AB|=5N, , Angle between two Vectors (6), , Angle between two vectors means smaller of the two angles between the vectors when they are, placed tail to tail by displacing either of the vectors parallel to Itself (i.e 0< <7)., , ow, wm, , , , Three vectors A,B,C are shown in the figure. Find angle between (i) A and B, (ii) B and G, (iii) A, , and C., - Bi * VE *, A . :, oe ; B é, , To find the angle between two vectors we connect the tails of the two vectors. We can shift B &, G such that, , tails of A,B and G are connected as shown in figure., , Now we can easily observe that angle between A and B is 60°,, B and G is 15° and between A and G is 75°., , , , Negative of Vector, It implies vector of same magnitude but opposite in direction., —7z —, >, , A -A

Page 3 :
3.4, , 3.5, , Equality of Vectors., Vectors having equal magnitude and same direction are called equal vectors, , 8, =|BI=|, , it |A|=1B1=IC), and A=B=C, then A=B=C, , Collinear vectors :, Any two vectors are co-linear then one can be express in the term of other., , a = Ab (where 2 is a constant), Co-initial vector : If two or more vector start from same point then they called co-initial vector., , , , here A, B, C, D are co-initial., , Coplanar vectors:, , Three (or more) vectors are called coplanar vectors if they lie in the same plane or are parallel to the, same plane. Two.(free) vectors.are always coplanar., , Important points, , If the frame of reference is translated or rotated the vector does not change (though its components, may change)., , , , Two vectors are called equal if their magnitudes and directions are same, and they represent values of, same physical quantity., , Multiplication and division of a vector by a scalar, Multiplying a vector A with a positive number 1 gives a vector (=a A) whose magnitude become 4, , times but the direction is the same as that of A . Multiplying a vector A bya negative number A gives, a vector § whose direction is opposite to the direction of A and whose magnitude is -A times | A|., , The division of vector A by a non-zero scalar m is defined as multiplication of A by +., , At here A and B are co-linear vector

Page 4 :
4.1, , 4.2, , Aphysical quantity (m = 3kg) is multiplied by a vector 4 such that F = ma. Find the magnitude, and direction of F if, @i) a =3m/s* East wards, , ii) a = -4 m/? North wards, , (i) F=ma=3x3ms~ East wards, = 9 N East wards, , (ii), F=ma=3x(-4)N North wards, , = -12.N North wards, = 12 N South wards, , LAWS OF ADDITION AND SUBTRACTION OF VECTORS :, , Triangle rule of addition : Steps for additing two vector representing same physical quantity by, triangle law., , (i) Keep vectors s.t. tail of one vector coincides with head of other., (ii) Join tail of first to head of the other by a line with arrow at head of the seconds, (iii) This new vector is the sum of two vectors. (also called reultant), , a D, , ow ©, , (i) (ii) (lil) AB+CD=AD, A—— 8B A Ao, , AB, Take example here., A boy moves 4 m south and then 5 m in direction 37° E of N. Find resultant displacement., , Polygon Law of addition :, , This law is used for adding more than two vectors. This is extension of triangle law of addition. We, keep on arranging vectors s.t. tail of next vector lies on head of former., , When we connect the tail of first vector to head of last we get resultant of all the vectors., , , , Note : P= (a+6)+e)+4 = (G+a+a)+4 [Associative Law]

Page 5 :
aaa, , Parallelogram law of addition :, , Steps:, , (i) Keep two vectors such that there tails coincide., , (ii) Draw parallel vectors to both of them considering both of them as sides of a parallelogram., , (iii) Then the diagonal drawn from the point where tails coincide represents the sum of two vectors,, with its tail at point of coincidence of the two vectors., , 5, (i) fs (ii, , Note: AC=4+b and AC=b+a thus a+b=b+a [Cummutative Law], , , , Note : Angle between 2 vectors is the angle between their positive directions., , Suppose angle between these two vectors is 6, and |a[-a,|b|=b, (AD)? = (AE)? + (DE)?, = (AB + BE)? + (DE)?, = (a + bcos 6)? + (bsin 6)?, = a? + b? cos’ + 2ab cos 6 + b’ sin’o, =a? +b? + 2abcos@, , , , , , Thus;AD = J/g? +b?4+2abcosé, , or |@+b|= Va* +b? + 2abcose, , angle a with vector a is, , DE bsiné, tana = 2e = (a+bcose), Important points :, , To a vector, only a vector of same type can be added that represents the same physical quantity and, the resultant, is also a vector of the same type., , As R = [A? + B? + 2AB cos6]”” so R will be maximum when, cos 6 = max = 1,, , i.e., @ = 0°, i.e. vectors are like or parallel and R,,, = A+ B., , | AIB| and angle between them 6 then R = 2Acose/2, , | A]B| and angle between them x -@ then R = 2Asin@/2, , The resultant will be minimum if, cos @ = min = - 1, i.e., 6 = 180°, i.e. vectors areantiparallel and R_,, = A-B., , If the vectors A and B are orthogonal, i.e., @ = 90°, R= VA? +B?