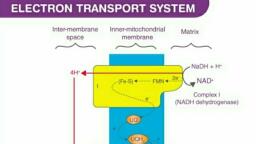
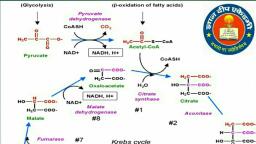
Page 1 :
Newton's Laws of motion, , 177, , Chapter, , 4, , Newton's Laws of Motion, Point Mass, (1) An object can be considered as a point object if during motion in, a given time, it covers distance much greater than its own size., , (7) If two objects of different masses have same momentum, the, lighter body possesses greater velocity., p  m1v1  m 2v 2 = constant, , , , (2) Object with zero dimension considered as a point mass., (3) Point mass is a mathematical concept to simplify the problems., , i.e. v , , Inertia, , 1, m, , [As p is constant], (8) For a given body p  v, , (1) Inherent property of all the bodies by virtue of which they, cannot change their state of rest or uniform motion along a straight line by, their own is called inertia., (2) Inertia is not a physical quantity, it is only a property of the, body which depends on mass of the body., , v1 m 2, , v 2 m1, , (9) For different bodies moving with same velocities p  m, p, , m = constant, , p, , v = constant, , (3) Inertia has no units and no dimensions, (4) Two bodies of equal mass, one in motion and another is at rest,, possess same inertia because it is a factor of mass only and does not depend, upon the velocity., , Linear Momentum, , Fig : 4.2, , v, , Fig : 4.3, , m, , (1) Linear momentum of a body is the quantity of motion contained, in the body., , Newton’s First Law, , (2) It is measured in terms of the force required to stop the body in, unit time., , A body continue to be in its state of rest or of uniform motion along, a straight line, unless it is acted upon by some external force to change the, state., , (3) It is also measured as the product of the mass of the body and, its velocity i.e., Momentum = mass × velocity., If a body of mass m is moving with velocity v then its linear, momentum p is given by p  m v, (4) It is a vector quantity and it’s direction is the same as the, direction of velocity of the body., (5) Units : kg-m/sec [S.I.], g-cm/sec [C.G.S.], (6) Dimension : [MLT 1 ], v, p = constant, , Fig : 4.1, , m, , (1) If no net force acts on a body, then the velocity of the body, cannot change i.e. the body cannot accelerate., (2) Newton’s first law defines inertia and is rightly called the law of, inertia. Inertia are of three types :, Inertia of rest, Inertia of motion and Inertia of direction., (3) Inertia of rest : It is the inability of a body to change by itself, its, state of rest. This means a body at rest remains at rest and cannot start, moving by its own., Example : (i) A person who is standing freely in bus, thrown, backward, when bus starts suddenly., When a bus suddenly starts, the force responsible for bringing bus, in motion is also transmitted to lower part of body, so this part of the body

Page 2 :
178 Newton's Laws of Motion, comes in motion along with the bus. While the upper half of body (say, above the waist) receives no force to overcome inertia of rest and so it stays, in its original position. Thus there is a relative displacement between the, two parts of the body and it appears as if the upper part of the body has, been thrown backward., , Note, , :  (i) If the motion of the bus is slow, the inertia of, , motion will be transmitted to the body of the person uniformly and so the, entire body of the person will come in motion with the bus and the person, will not experience any jerk., (ii) When a horse starts suddenly, the rider tends to fall backward, on account of inertia of rest of upper part of the body as explained above., (iii) A bullet fired on a window pane makes a clean hole through it,, while a ball breaks the whole window. The bullet has a speed much greater, than the ball. So its time of contact with glass is small. So in case of bullet, the motion is transmitted only to a small portion of the glass in that small, time. Hence a clear hole is created in the glass window, while in case of ball,, the time and the area of contact is large. During this time the motion is, transmitted to the entire window, thus creating the cracks in the entire, window., , Cracks by the ball, , Hole by the bullet, Fig, :, 4.4, (iv) In the arrangement shown in the figure :, , (a) If the string B is pulled with a sudden jerk then it will experience, tension while due to inertia of rest of mass M this force, will not be transmitted to the string A and so the string, A, B will break., (b) If the string B is pulled steadily the force, applied to it will be transmitted from string B to A, through the mass M and as tension in A will be greater, than in B by Mg (weight of mass M), the string A will, break., , M, , (5) Inertia of direction : It is the inability of a body to change by, itself it's direction of motion., , Example : (i) When a stone tied to one end of a string is whirled, and the string breaks suddenly, the stone flies off along the tangent to the, circle. This is because the pull in the string was forcing the stone to move, in a circle. As soon as the string breaks, the pull vanishes. The stone in a, bid to move along the straight line flies off tangentially., (ii) The rotating wheel of any vehicle throw out mud, if any,, tangentially, due to directional inertia., (iii) When a car goes round a curve suddenly, the person sitting, inside is thrown outwards., , Newton’s Second Law, (1) The rate of change of linear momentum of a body is directly, proportional to the external force applied on the body and this change, takes place always in the direction of the applied force., , (2) If a body of mass m, moves with velocity v then its linear, , , , momentum can be given by p  m v and if force F is applied on a body,, then, ,  d p, dp, F, FK, dt, dt, ,  dp, or F , (K = 1 in C.G.S. and S.I. units), dt, ,  d, , , dv, or F  (m v )  m,  ma, dt, dt, , dv, (As a ,  acceleration produced in the body), dt, , ,  F  ma, Force = mass  acceleration, , B, , (v) If we place a coin on smooth piece of card, Fig : 4.5, board covering a glass and strike the card board piece, suddenly with a finger. The cardboard slips away and the coin falls into the, glass due to inertia of rest., (vi) The dust particles in a carpet falls off when it is beaten with a, stick. This is because the beating sets the carpet in motion whereas the dust, particles tend to remain at rest and hence separate., (4) Inertia of motion : It is the inability of a body to change by itself, its state of uniform motion i.e., a body in uniform motion can neither, accelerate nor retard by its own., , Example : (i) When a bus or train stops suddenly, a passenger sitting, inside tends to fall forward. This is because the lower part of his body, comes to rest with the bus or train but the upper part tends to continue its, motion due to inertia of motion., , Force, (1) Force is an external effect in the form of a push or pull which, (i) Produces or tries to produce motion in a body at rest., (ii) Stops or tries to stop a moving body., (iii) Changes or tries to change the direction of motion of the body., Table 4.1 : Various condition of force application, F, u=0, , v=0, , Body remains at rest. Here force is, trying to change the state of rest., , F, u=0, , v>0, , Body starts moving. Here force, changes the state of rest., , (ii) A person jumping out of a moving train may fall forward., (iii) An athlete runs a certain distance before taking a long jump., This is because velocity acquired by running is added to velocity of the, athlete at the time of jump. Hence he can jump over a longer distance., , F, u0, , v>u, , In a small interval of time, force, increases the magnitude of speed and, direction of motion remains same.

Page 3 :
Newton's Laws of motion, , u, , F, , v<u, v, , (9) Out of so many natural forces, for distance 10 15, nuclear force is strongest while gravitational force weakest., Fnuclear  Felectromagnetic  Fgravitational, , In a small interval of time, force, decreases the magnitude of speed and, direction of motion remains same., , (10) Ratio of electric force and gravitational force between two, , In uniform circular motion only, direction of velocity changes, speed, remains constant. Force is always, perpendicular to velocity., , F, F, v, , electron’s Fe / Fg  10 43  Fe  Fg, (11) Constant force : If the direction and magnitude of a force is, constant. It is said to be a constant force., (12) Variable or dependent force :, (i) Time dependent force : In case of impulse or motion of a charged, particle in an alternating electric field force is time dependent., (ii) Position dependent force : Gravitational force between two, Gm1m 2, bodies, r2, , In non-uniform circular motion,, elliptical, parabolic or hyperbolic, motion force acts at an angle to the, direction of motion. In all these, motions. Both magnitude and, direction of velocity changes., , v, , F = mg, , (2) Dimension : Force = mass  acceleration, , or Force between two charged particles , , [F]  [M ][LT 2 ]  [MLT 2 ], , (3) Units :, , Gravitational units : (i) Kilogram-force (M.K.S.) (ii) Gram-force, (C.G.S), , Newton : One Newton is that force which produces an, acceleration of 1 m / s 2 in a body of mass 1 Kilogram., 2, , Dyne : One dyne is that force which produces an acceleration, of 1cm / s 2 in a body of mass 1 gram ., , ., , 4 0 r 2, , Force on charged particle in a magnetic field (qvB sin ), (13) Central force : If a position dependent force is directed towards, or away from a fixed point it is said to be central otherwise non-central., , Example : Motion of Earth around the Sun. Motion of electron in an, atom. Scattering of -particles from a nucleus., Electron, F, Sun, , Earth, , acceleration of 9.8 m / s 2 in a body of mass 1 kg .,  1 kg-f = 9.80 Newton, , Gram-force : It is that force which produces an acceleration, of 980cm / s 2 in a body of mass 1 gm .,  1 gm-f = 980 Dyne, , , (4) F  m a formula is valid only if force is changing the state of, rest or motion and the mass of the body is constant and finite., ,  d, , dv  dm, (5) If m is not constant F  (m v )  m, v, dt, dt, dt, (6) If force and acceleration have three component along x, y and z, axis, then, , , F  Fxˆi  Fy ˆj  Fz kˆ and a  axˆi  ay ˆj  az kˆ, From above it is clear that Fx  ma x , Fy  ma y , Fz  ma z, (7) No force is required to move a body uniformly along a straight, line with constant speed., , , F  ma,  F  0 (As a  0 ), (8) When force is written without direction then positive force, means repulsive while negative force means attractive., Example : Positive force – Force between two similar charges, Negative force – Force between two opposite charges, , +, , +, , Nucleus, an, , –, , F, , F, ,  1 Dyne  1gm cm / sec 2, Relation between absolute units of force 1 Newton  10 5 Dyne, Kilogram-force : It is that force which produces, , q1 q 2, , (iii) Velocity dependent force : Viscous force (6rv), , Absolute units : (i) Newton (S.I.) (ii) Dyne (C.G.S), , 1 Newton  1kg m / s, , 179, , +, , -particle, , Nucleus, , Fig : 4.6, , (14) Conservative or non conservative force : If under the action of a, force the work done in a round trip is zero or the work is path, independent, the force is said to be conservative otherwise non conservative., Example : Conservative force : Gravitational force, electric force,, elastic force., Non conservative force : Frictional force, viscous force., (15) Common forces in mechanics :, (i) Weight : Weight of an object is the force with which earth attracts it., It is also called the force of gravity or the gravitational force., (ii) Reaction or Normal force : When a body is placed on a rigid, surface, the body experiences a force which is perpendicular to the surfaces, in contact. Then force is called ‘Normal force’ or ‘Reaction’., R, , R, , , mg cos, mg, mg,  of taut string, rope or, (iii) Tension : The force exerted by the end, : 4.7 (applied) force is called the tension., Fig : 4.8, chain againstFigpulling, The direction of, tension is so as to pull the body., , T=F, , Fig : 4.9, , (iv) Spring force : Every spring resists any attempt to change its, length. This resistive force increases with change in length. Spring force is

Page 4 :
180 Newton's Laws of Motion, given by F  Kx ; where x is the change in length and K is the spring, constant (unit N/m)., , (5) If F AB = force exerted on body A by body B (Action) and F BA =, force exerted on body B by body A (Reaction), Then according to Newton’s third law of motion F AB   F BA, (6) Example : (i) A book lying on a table exerts a force on the table, which is equal to the weight of the book. This is the force of action., , F = – Kx, , R, , mg, , x, Fig : 4.10Force, Equilibrium of Concurrent, , (1) If all the forces working on a body are acting on the same point,, then they are said to be concurrent., (2) A body, under the action of concurrent forces, is said to be in, equilibrium, when there is no change in the state of rest or of uniform, motion along a straight line., (3) The necessary condition for the equilibrium of a body under the, action of concurrent forces is that the vector sum of all the forces acting on, the body must be zero., , (4) Mathematically for equilibrium, Fnet  0 or  Fx  0 ;, , , , The table supports the book, by exerting an equal force on the book., Fig : 4.13, This is the force of reaction., As the system is at rest, net force on it is zero. Therefore force of, action and reaction must be equal and opposite., (ii) Swimming is possible due to third law of motion., (iii) When a gun is fired, the bullet moves forward (action). The gun, recoils backward (reaction), (iv) Rebounding of rubber ball takes place due to third law of, motion., ,  Fy  0 ; ,  Fz  0, (5) Three concurrent forces will be in equilibrium, if they can be, represented completely by three sides of a triangle taken in order., F2, , B, , R, , , C, , R cos, F3, , F1, , A concurrent forces in equilibrium, (6) Lami’s Theorem : For three, Fig : 4.11, F1, F2, F3, , , sin sin  sin, F1, , , , , , F2, , , , F3, , Newton’s Third Law, , R sin , , Fig : 4.12, , To every action, there is always an equal (in magnitude) and, opposite (in direction) reaction., (1) When a body exerts a force on any other body, the second body, also exerts an equal and opposite force on the first., (2) Forces in nature always occurs in pairs. A single isolated force is, not possible., (3) Any agent, applying a force also experiences a force of equal, magnitude but in opposite direction. The force applied by the agent is called, ‘Action’ and the counter force experienced by it is called ‘Reaction’., (4) Action and reaction never act on the same body. If it were so,, the total force on a body would have always been zero i.e. the body will, always remain in equilibrium., , (v) While walking a person, the ground in the backward, Fig :presses, 4.14, direction (action) by his feet. The ground pushes the person in forward, direction with an equal force (reaction). The component of reaction in, horizontal direction makes the person move forward., (vi) It is difficult to walk on sand or ice., (vii) Driving a nail into a wooden block without holding the block is, difficult., , Frame of Reference, (1) A frame in which an observer is situated and makes his, observations is known as his ‘Frame of reference’., (2) The reference frame is associated with a co-ordinate system and, a clock to measure the position and time of events happening in space. We, can describe all the physical quantities like position, velocity, acceleration, etc. of an object in this coordinate system., (3) Frame of reference are of two types : (i) Inertial frame of, reference (ii) Non-inertial frame of reference., (i) Inertial frame of reference :, (a) A frame of reference which is at rest or which is moving with a, uniform velocity along a straight line is called an inertial frame of reference., (b) In inertial frame of reference Newton’s laws of motion holds, good., (c) Inertial frame of reference are also called unaccelerated frame of, reference or Newtonian or Galilean frame of reference., (d) Ideally no inertial frame exist in universe. For practical purpose a, frame of reference may be considered as inertial if it’s acceleration is, negligible with respect to the acceleration of the object to be observed.

Page 5 :
Newton's Laws of motion, (e) To measure the acceleration of a falling apple, earth can be, considered as an inertial frame., (f) To observe the motion of planets, earth can not be considered as, an inertial frame but for this purpose the sun may be assumed to be an, inertial frame., Example : The lift at rest, lift moving (up or down) with constant, velocity, car moving with constant velocity on a straight road., (ii) Non-inertial frame of reference, (a) Accelerated frame of references are called non-inertial frame of, reference., (b) Newton’s laws of motion are not applicable in non-inertial frame, of reference., Example : Car moving in uniform circular motion, lift which is, moving upward or downward with some acceleration, plane which is taking, off., , 181, , I   F dt  Fav . t  p  constant, , So if time of contact t is increased, average force is decreased (or, diluted) and vice-versa., (i) In hitting or kicking a ball we decrease the time of contact so, that large force acts on the ball producing greater acceleration., (ii) In catching a ball a player by drawing his hands backwards, increases the time of contact and so, lesser force acts on his hands and his, hands are saved from getting hurt., , Impulse, , Fig : 4.17, , (1) When a large force works on a body for very small time interval,, it is called impulsive force., An impulsive force does not remain constant, but changes first from, zero to maximum and then from maximum to zero. In such case we, measure the total effect of force., (2) Impulse of a force is a measure of total effect of force., t, , (3) I  t 2 F dt ., 1, , (4) Impulse is a vector quantity and its direction is same as that of, force., , (iii) In jumping on sand (or water) the time of contact is increased, due to yielding of sand or water so force is decreased and we are not, injured. However if we jump on cemented floor the motion stops in a very, short interval of time resulting in a large force due to which we are, seriously injured., (iv) An athlete is advised to come to stop slowly after finishing a fast, race, so that time of stop increases and hence force experienced by him, decreases., (v) China wares are wrapped in straw or paper before packing., , (5) Dimension : [ MLT 1 ], , Law of Conservation of Linear Momentum, , (6) Units : Newton-second or Kg-m- s 1 (S.I.), , If no external force acts on a system (called isolated) of constant, mass, the total momentum of the system remains constant with time., , Dyne-second or gm-cm- s, , 1, , (C.G.S.), (7) Force-time graph : Impulse is equal to the area under F-t curve., If we plot a graph between force and time, the area under the curve, and time axis gives the value of impulse., I  Area between curve and time axis, , 1,   Base  Height, 2, , , Force, , Time, , (2) Law of conservation of linear momentum is independent of, frame of reference, though linear momentum depends on frame of, reference., , 1, , I   t 2 F dt  Fav  t 2 dt  Fav t, , (9) From Newton’s second law, , , F, , or, , dp, dt, t2, , (3) Conservation of linear momentum is equivalent to Newton’s, third law of motion., , F, , For a system of two particles in absence of external force, by law of, conservation of linear momentum., , Fav, Impulse, , p2, ,  t1 F dt   p1 d p, , ,  I  p 2  p 1  p, , t, t1, , t, Fig : 4.16, , t2, , i.e. The impulse of a force is equal to the change in momentum., This statement is known as Impulse momentum theorem., Examples : Hitting, kicking, catching, jumping, diving, collision etc., In all these cases an impulse acts., , , , This equation shows that in absence of external force for a closed, system the linear momentum of individual particles may change but their, sum remains unchanged with time., , Fav is the average magnitude of the force then, t, , , , or m1 v1  m 2 v 2  m 3 v 3  ....  constant, , F, t, , 1, , , , In the absence of external force F  0 then p  constant, , , , 1, Ft, 2, , t, , dp, dt, , i.e., p  p 1  p 2  p 3  ....  constant., , Fig : 4.15, , (8) If, , (1) According to this law for a system of particles F , , p 1  p 2  constant., , , ,  m1v1  m 2v 2  constant., , Differentiating above with respect to time, , , , , dv, dv, m1 1  m 2 2  0  m1a1  m 2 a2  0  F1  F 2  0, dt, dt,  F 2   F1

Page 6 :
182 Newton's Laws of Motion, i.e. for every action there is an equal and opposite reaction which is, Newton’s third law of motion., (4) Practical applications of the law of conservation of linear, momentum, (i) When a man jumps out of a boat on the shore, the boat is, pushed slightly away from the shore., , Let m 0  initial mass of rocket,, , m = mass of rocket at any instant ‘t’ (instantaneous mass), , (ii) A person left on a frictionless surface can get away from it by, blowing air out of his mouth or by throwing some object in a direction, opposite to the direction in which he wants to move., , m r  residual mass of empty container of the rocket, , (iii) Recoiling of a gun : For bullet and gun system, the force exerted, by trigger will be internal so the momentum of the system remains, unaffected., , v = velocity of rocket at any instant ‘t’ (instantaneous velocity), , , vG, , u = velocity of exhaust gases,, , dm,  rate of change of mass of rocket = rate of fuel consumption, dt, , , vB, , = rate of ejection of the fuel., dm,  mg, dt, , (a) Thrust on the rocket : F  u, Fig : 4.18, , Let m G  mass of gun, m B  mass of bullet,, v G  velocity of gun, v B  velocity of bullet, , Initial momentum of system = 0, , , Final momentum of system  m GvG  m Bv B, , By the law of conservation of linear momentum, , , m Gv G  m Bv B  0, , m , So recoil velocity v G   B vB, mG, , 1, i.e. higher the mass of gun, lesser the velocity of, mG, , recoil of gun., (c) While firing the gun must be held tightly to the shoulder, this, would save hurting the shoulder because in this condition the body of the, shooter and the gun behave as one body. Total mass become large and, recoil velocity becomes too small., vG , , mG, , F  u, , dm, (if effect of gravity is neglected), dt, a, , (b) Acceleration of the rocket :, , and if effect of gravity is neglected a , , u dm, g, m dt, , u dm, m dt, , (c) Instantaneous velocity of the rocket :, , , (a) Here negative sign indicates that the velocity of recoil v G is, opposite to the velocity of the bullet., , (b) v G , , Here negative sign indicates that direction of thrust is opposite to, the direction of escaping gases., , m, v  u log e  0,  m, , ,   gt, , , and, , of, , if, , effect, , gravity, , is, , neglected, , m , v  u loge  0 ,  m , , m ,  2 .303u log10  0 ,  m , m, (d) Burnt out speed of the rocket : vb  v max  u loge  0,  mr, , , , , , , The speed attained by the rocket when the complete fuel gets burnt is, called burnt out speed of the rocket. It is the maximum speed acquired by, the rocket., , 1,  m man, , (iv) Rocket propulsion : The initial momentum of the rocket on its, launching pad is zero. When it is fired from the launching pad, the exhaust, gases rush downward at a high speed and to conserve momentum, the, rocket moves upwards., , Free Body Diagram, In this diagram the object of interest is isolated from its, surroundings and the interactions between the object and the surroundings, are represented in terms of forces., , Example :, , v, , m, , T, , T, , a, , a, , m1, , m2, , , , R1, u, , u, Fig : 4.19, , m1a, , , , T, , T, , m1, , m2, , m1g cos, , m1g sin , Free body diagram of, , R2, , m2g cos, Free body diagram of, , a, , m2g sin

Page 7 :
Newton's Laws of motion, , 183, , Apparent Weight of a Body in a Lift, When a body of mass m is placed on a weighing machine which is, placed in a lift, then actual weight of the body is mg., R, , This acts on a weighing machine which offers a reaction R given by, the reading of weighing machine. This reaction exerted by the surface of, contact on the body is the apparent weight of the body., , Table 4.2 : Apparent weight in a lift, Condition, , Figure, , Velocity, , Acceleration, , Reaction, , Conclusion, , LIFT, , R, v=0, , Lift is at rest, , a=0, , R – mg = 0,  R = mg, , Apparent weight, = Actual weight, , a=0, , R – mg = 0,  R = mg, , Apparent weight, = Actual weight, , a<g, , R – mg = ma, R = m(g + a), , Apparent weight, > Actual weight, , a=g, , R – mg = mg, R = 2mg, , Apparent weight, = 2 Actual weight, , a<g, , mg – R = ma,  R = m(g – a), , Apparent weight < Actual, weight, , a=g, , mg – R = mg, R=0, , Apparent weight, = Zero (weightlessness), , a>g, , mg – R = ma, R = mg – ma, , Apparent weight negative, means the body will rise, , mg, Spring Balance, , Fig : 4.21, , mg, , LIFT, Lift moving upward or, downward with, constant velocity, , R, v = constant, Spring Balance, , mg, LIFT, Lift accelerating, upward at the rate of, 'a’, , R, a, , v = variable, , g, , v = variable, , a, , v = variable, , g, , v = variable, , Spring Balance, , mg, LIFT, Lift accelerating, upward at the rate of, ‘g’, , R, , Spring Balance, , mg, LIFT, Lift accelerating, downward at the rate, of ‘a’, , R, , Spring Balance, , mg, LIFT, Lift accelerating, downward at the rate, of ‘g’, , R, , Spring Balance, , mg, Lift accelerating, downward at the rate, , v = variable, , LIFT, , R, a>g, Spring Balance, , mg

Page 8 :
184 Newton's Laws of Motion, of a(>g), , R = – ve, , from the floor of the lift, and stick to the ceiling of, the lift.

Page 9 :
Newton's Laws of motion, , Acceleration of Block on Horizontal Smooth Surface, R, , (1) When a pull is horizontal, , R = mg, , a, , F, , and F = ma, mg, Fig : 4.22, , (2) When a pull is acting at an angle () to the horizontal (upward), F sin, , R + F sin  = mg, , R, ,  R = mg – F sin, , , , m, , F cos , m, , R, a, , , F cos, , mg, , ,  mg, , Fig : 4.23, , (3) When a push is acting at an angle () to the horizontal, (downward), R, , F, , R = mg + F sin, , a, , , , and F cos = ma, a, , Normal reaction R = mg cos, Force along a inclined plane, F = mg sin ; ma = mg sin, a = g sin, (2) When a inclined plane given a horizontal acceleration ‘b’, Since the body lies in an accelerating frame, an inertial force (mb), acts on it in the opposite direction., , F, , and F cos = ma,  a, , Acceleration of Block on Smooth Inclined Plane, (1) When inclined plane is at rest, , m, ,  a = F/m, , F cos , m, , m, , F cos, , F sin, , Condition, , mb, b, , mg cos +mb sin , , Fig : 4.25, , Normal reaction R = mg cos + mb sin, and ma = mg sin  – mb cos ,  a = g sin – b cos, , Note : , , The condition for the body to be at rest relative to the, , inclined plane : a = g sin – b cos = 0, , mg, , Motion of Blocks In Contact, , 185, ,  b = g tan, , Fig : 4.24, , Free body diagram, , Equation, , Force and acceleration, , a, F, B, , m1, , A, F, , m1, , f, , F  f  m1a, , a, , F, m1  m 2, , f  m 2a, , f, , m2F, m1  m 2, , f  m1a, , a, , F, m1  m 2, , F  f  m 2a, , f, , m1 F, m1  m 2, , a, , m2, f, , m2, a, m1, , B, A, m1, , m2, , f, , a, , F, f, , m2, , F, , a, F, , F, , A, , B, , m1, , m2, , C, , m1, , m3, , a, f1, , m2, , f1, , f2, , a, f2, , f1, , a, A, , B, , m1, , m2, , m3, , f1, F, , m2, , f2, , a, f2, , a, , F, m1  m 2  m 3, , f1  f2  m 2a, , f1 , , (m 2  m 3 )F, m1  m 2  m 3, , f2  m 3 a, , f2 , , m3 F, m1  m 2  m 3, , f1  m1a, , a, , F, m1  m 2  m 3, , f2  f1  m 2a, , f1 , , m1 F, m1  m 2  m 3, , m3, a, m1, , C, , F  f1  m1a, , m3, , F

Page 14 :
190 Newton's Laws of Motion, , m, , T2   M   a, 2, , , T2 , , T2  Tension at mid point of the rope, , L, , m, , a  F/m, , a, , x, , m = Mass of string, , m [(L – x)/L], , from the end where the force is, applied, , a, , L, , F1, A, , x, , M = Mass of uniform string, , A, , (M/L)x, , B, , F1  T , , F1, , T, a, , B, , M, , F2, , Lx , T , F,  L , , Lx , T m, a,  L , , T, , T = Tension in string at a distance x, , F2, , F  ma, , F, , F, , T, , (2 M  m ), F, 2(M  m ), , F1, , Mxa, L, , a, , x, , x, T  F1  1    F2  , L, , L, , F1  F2  Ma, , a, , L = Length of string, , T, , T' , , A, , A, , F1  F2, M, , T '  F  Mg, , M, (L  x )g  T, L, , L–x, L, , B, , T, , B, T, , T, , x, , T, B, , C, , x, , F, , M, Mass of segment BC    x,  L , , C, , T F, F, , Spring Balance and Physical Balance, (1) Spring balance : When its upper end is fixed with rigid support, and body of mass m hung from its lower end. Spring is stretched and the, weight of the body can be measured by the reading, of spring balance R  W  mg, , T F, , M, xg, L, , (2) Physical balance : In physical balance actually we compare the, mass of body in both the pans. Here we does not calculate the absolute, weight of the body., a, , b, , A, , B, O, , The mechanism of weighing machine is, same as that of spring balance., , Effect of frame of reference : In inertial, frame of reference the reading of spring balance, shows the actual weight of the body but in noninertial frame of reference reading of spring balance, increases or decreases in accordance with the, direction of acceleration, , M, xg, L, , R, , X, m, Fig : 4.26, , Fig : 4.27, , Y, , Here X and Y are the mass of the empty pan., (i) Perfect physical balance :, Weight of the pan should be equal i.e. X = Y, and the needle must in middle of the beam i.e. a = b.

Page 15 :
Newton's Law of motion 191, Effect of frame of reference : If the physical balance is perfect then, there will be no effect of frame of reference (either inertial or non-inertial), on the measurement. It is always errorless., a, , b, , A, , B, , According to Newton, time and space are absolute. The velocity of, observer has no effect on it. But, according to special theory of relativity, Newton’s laws are true, as long as we are dealing with velocities which are, small compare to velocity of light. Hence the time and space measured by two, observers in relative motion are not same. Some conclusions drawn by the, special theory of relativity about mass, time and distance which are as follows :, , O, , (1) Let the length of a rod at rest with respect to an observer is, , L0 . If the rod moves with velocity v w.r.t. observer and its length is L, then, L  L0 1  v 2 / c 2, , Y, X, , 4.28, (ii) False balance : When Fig, the: masses, of the pan are not equal then, balance shows the error in measurement. False balance may be of two types, , (a) If the beam of physical balance is horizontal (when the pans are, empty) but the arms are not equal, X  Y and a  b, , For rotational equilibrium about point ‘O’, Xa  Yb, , …(i), , In this physical balance if a body of weight W is placed in pan X, then to balance it we have to put a weight, , W1 in pan Y., , For rotational equilibrium about point ‘O’, (X  W )a  (Y  W1 )b, , …(ii), , Now if the pans are changed then to balance the body we have to, put a weight, , W2 in pan X., , For rotational equilibrium about point ‘O’, , where, c is the velocity of light., Now, as v increases L decreases, hence the length will appear, shrinking., (2) Let a clock reads T for an observer at rest. If the clock moves, with velocity v and clock reads T with respect to observer, then, T0, T , v2, 1 2, c, Hence, the clock in motion will appear slow., 0, , (3) Let the mass of a body is m 0 at rest with respect to an, observer. Now, the body moves with velocity v with respect to observer and, m0, its mass is m, then m , v2, 1 2, c, m is called the rest mass., Hence, the mass increases with the increases of velocity., 0, , (X  W2 )a  (Y  W )b, , …(iii), , From (i), (ii) and (iii), , Note :  If v  c, i.e., velocity of the body is very small w.r.t., velocity of light, then m  m 0 . i.e., in the practice there will be no change, in the mass., , True weight W  W1 W2, ,  If v is comparable to c, then m > m i.e., mass will increase., , (b) If the beam of physical balance is not horizontal (when the pans, are empty) and the arms are equal, , i.e. X  Y and a  b, In this physical balance if a body of weight W is placed in X Pan, then to balance it., We have to put a weight W in Y Pan, 1, , For equilibrium X  W  Y  W1, b, , a, A, , …(i), , 0, ,  If v  c, then m , , m0, , or m , 2, , m0,  . Hence, the, 0, , v, v2, mass becomes infinite, which is not possible, thus the speed cannot be equal, to the velocity of light.,  The velocity of particles can be accelerated up to a certain limit., Even in cyclotron the speed of charged particles cannot be increased beyond, a certain limit., 1, , B, O, , Y, X, , Fig : 4.29, , Now if pans are changed then to balance the body we have to put a, weight, , W2 in X Pan., For equilibrium X  W2  Y  W, From (i) and (ii), True weight W , , W1  W2, 2, , Modification of Newton’s Laws of motion, , …(ii), , , , , , , Inertia is proportional to mass of the body., Force cause acceleration., In the absence of the force, a body moves along a straight line path., , A system or a body is said to be in equilibrium, when the net force, acting on it is zero.,   ,  If a number of forces F1 , F2 , F3 , ......... act on the body, then it is, , , , , in equilibrium when F1  F2  F3  .........  0

Page 16 :
192 Newton's Laws of Motion,  A body in equilibrium cannot change the direction of motion.,  Four types of forces exist in nature. They are – gravitation (Fg ) ,, electromagnetic (Fem ) , weak force (Fw ) and nuclear force (Fn ) ., (Fg ) : (Fw ) : (Fem ) : (Fn ) : : 1 : 10 : 10 : 10, 25, , 36, , 38, ,  If a body moves along a curved path, then it is certainly acted upon, by a force., , 2l, g sin, , t, , , , 1, sin, , 2h, g, , (iv) If the angle of inclination is changed keeping the height constant, then, t1 sin 2, , t2, sin 1, ,  A single isolated force cannot exist., ,  For an isolated system (on which no external force acts), the total, ,  Forces in nature always occur in pairs., , momentum remains conserved (Law of conservation of momentum)., ,  Newton's first law of the motion defines the force., ,  The change in momentum of a body depends on the, ,  Absolute units of force remains the same throughout the universe, , magnitude and direction of the applied force and the period of, time over which it is applied i.e. it depends on its impulse., , while gravitational units of force varies from place to place as they, depend upon the value of ‘g’., ,  Newton's second law of motion gives the measure of force i.e. F =, ma., ,  Guns recoil when fired, because of the law of conservation of, momentum. The positive momentum gained by the bullet is equal, to negative recoil momentum of the gun and so the total, momentum before and after the firing of the gun is zero., ,  Force is a vector quantity.,  Absolute units of force are dyne in CGS system and newton (N) in, , , ,  Recoil velocity of the gun is V , , SI., ,  1 N = 10 dyne., 5, ,  Gravitational units of force are gf (or gwt) in CGS system and kgf, (or kgwt) in SI., ,  1 gf = 980 dyne and 1 kgf = 9.8 N,  The beam balance compares masses., , , ,  where m = mass of bullet, M = mass of gun and v = muzzle, velocity of bullet., ,  The rocket pushes itself forwards by pushing the jet of exhaust, gases backwards., ,  Upthrust on the rocket = u , ,  Acceleration of a horse-cart system is, a, , HF, M m, , where H = Horizontal component of reaction; F = force of friction; M =, mass of horse; m = mass of cart., ,  The weight of the body measured by the spring balance in a lift is, equal to the apparent weight., ,  Apparent weight of a freely falling body = ZERO, (state of, weightlessness)., ,  If the person climbs up along the rope with acceleration a, then, , m , v, M, , dm, ., dt, , where u = velocity of escaping gases relative to rocket and, , dm,  rate, dt, , of consumption of fuel., ,  Initial thrust on rocket = m(g + a), where a is the acceleration of, the rocket., ,  Upward acceleration of rocket =, , , u dm, , ., m dt, , , ,  Impulse, I  F  t  change in momentum, , tension in the rope will be m(g+a), ,  Unit of impulse is N-s., ,  If the person climbs down along the rope with acceleration, then, ,  Action and reaction forces never act on the same body. They act on, , tension in the rope will be m(g – a), ,  When the person climbs up or down with uniform speed, tension, , different bodies. If they act on the same body, the resultant force on the, body will be zero i.e., the body will be in equilibrium., , in the string will be mg., ,  Action and reaction forces are equal in magnitude but opposite in, ,  A body starting from rest moves along a smooth inclined plane of, , direction., , length l, height h and having angle of inclination  ., (i) Its acceleration down the plane is g sin  ., (ii) Its velocity at the bottom of the inclined plane will be, 2 gh  2 gl sin ., , (iii) Time taken to reach the bottom will be, ,  Action and reaction forces act along the line joining the centres of, two bodies., ,  Newton's third law is applicable whether the bodies are at rest or, in motion., ,  The non-inertial character of the earth is evident from the fact that, a falling object does not fall straight down but slightly deflects to the