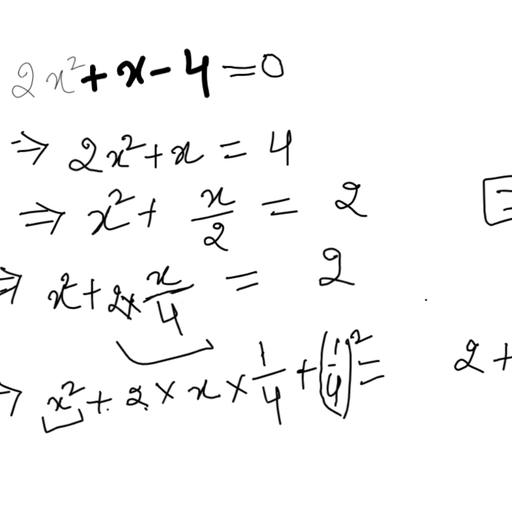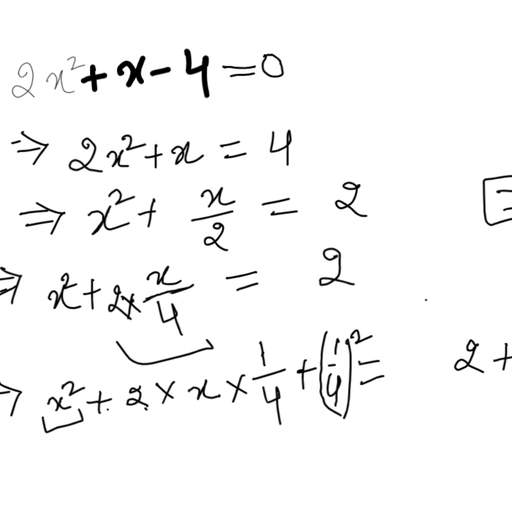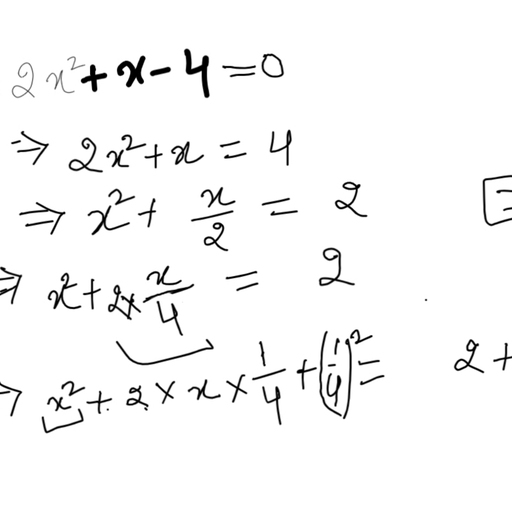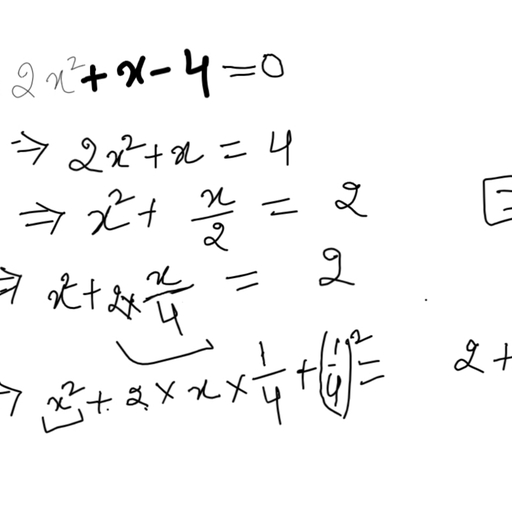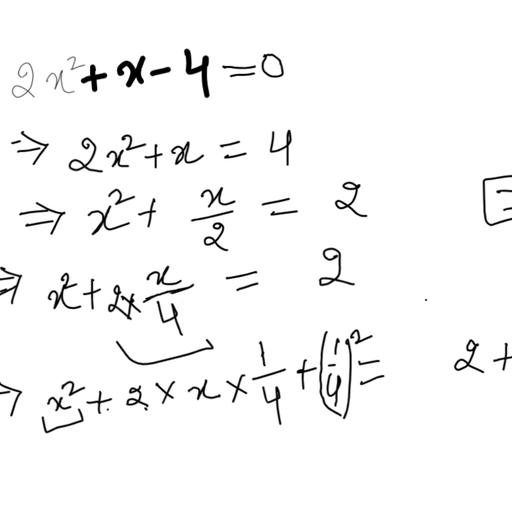Page 1 :
NCERT Solutions for Class 7 Maths Chapter 12, Algebraic Expressions Class 7, Chapter 12 Algebraic Expressions Exercise 12.1, 12.2, 12.3, 12.4 Solutions, << Previous Chapter 11 : Perimeter and AreaNext Chapter 13 : Exponents and Powers >>, , Exercise 12.1 : Solutions of Questions on Page Number : 234, Q1 :, Get the algebraicexpressions in the following cases using variables, constants and arithmetic operations., (i), , Subtraction of z from y., , (ii) One-half of the sum of numbers x and y., (iii) The number z multiplied by itself., (iv) One-fourth of the product of numbers p and q., (v) Numbers x and y both squared and added., (vi) Number 5 added to three times the product of number m and n., (vii) Product of numbers y and z subtracted from 10., (viii)Sum of numbers a and b subtracted from their product., Answer :, (i) y - z, , (ii), , (iii) z2, , (iv), (v) x2 + y2, (vi) 5 + 3 (mn), (vii) 10 - yz (viii) ab - (a + b)
Page 2 :
Q2 :, (i) Identify the terms and their factors in the following expressions Show, the terms and factors by tree diagrams., , (a) x - 3 (b) 1 + x + x2 (c) y - y3, (d), , (e) - ab + 2b2 - 3a2, , (ii) Identify terms and factors in the expressions given below:, (a) - 4x + 5 (b) - 4x + 5y (c) 5y + 3y2, (d), , (e) pq + q, , (f) 1.2 ab - 2.4 b + 3.6 a (g), (h) 0.1p2 + 0.2 q2
Page 3 :
Answer :
Page 15 :
<< Previous Chapter 11 : Perimeter and AreaNext Chapter 13 : Exponents and Powers >>, , Exercise 12.3 : Solutions of Questions on Page Number : 242, Q1 :, If m = 2, find the value of:, (i) m - 2 (ii) 3m - 5 (iii) 9 - 5m, , (iv) 3m2 - 2m - 7 (v), Answer :, (i) m - 2 = 2 - 2 = 0, (ii) 3m - 5 = (3 × 2) - 5 = 6 - 5 = 1, (iii) 9 - 5m = 9 - (5 × 2) = 9 - 10 = - 1, (iv) 3m2 - 2m - 7 = 3 × (2 × 2) - (2 × 2) - 7, = 12 - 4 - 7 = 1, , (v), , Q2 :, If p = -2, find the value of:, (i) 4p + 7, (ii) -3p2 + 4p + 7, (iii) -2p3 - 3p2 + 4p + 7, Answer :, (i) 4p + 7 = 4 x (-2) + 7 = - 8 + 7 = -1, (ii) - 3p2 + 4p + 7 = -3 (-2) x (-2) + 4 x (-2) + 7, = - 12 - 8 + 7 = -13, (iii) -2p3 - 3p2 + 4p + 7, = -2 (-2) x (-2) x (-2) - 3 (-2) x (-2) + 4 x (-2) + 7, = 16 - 12 - 8 + 7 = 3, , Q3 :, Find the value of the following expressions, when x = - 1:, (i) 2x - 7 (ii) - x + 2 (iii) x2 + 2x + 1, (iv) 2x2 - x - 2, Answer :, (i) 2x - 7, = 2 x (-1) - 7 = -9, (ii) - x + 2 = - (-1) + 2 = 1 + 2 = 3
Page 16 :
(iii) x2 + 2x + 1 = (-1) x (-1) + 2 x (-1) + 1, =1-2+1=0
Page 17 :
(iv) 2x2 - x - 2 = 2 (-1) x (-1) - (-1) - 2, =2+1-2=1, , Q4 :, If a = 2, b = - 2, find the value of:, (i) a2 + b2 (ii) a2 + ab + b2 (iii) a2 - b2, Answer :, (i) a2 + b2, = (2)2 + (-2)2 = 4 + 4 = 8, (ii) a2 + ab + b2, = (2 x 2) + 2 x (-2) + (-2) x (-2), =4-4+4=4, (iii) a2 - b2 = (2)2 - (-2)2 = 4 - 4 = 0, , Q5 :, When a = 0, b = - 1, find the value of the given expressions:, (i) 2a + 2b (ii) 2a2 + b2 + 1, (iii) 2a2 b + 2ab2 + ab (iv) a2 + ab + 2, Answer :, (i) 2a + 2b = 2 x (0) + 2 x (-1) = 0 - 2 = -2, (ii) 2a2 + b2 + 1, = 2 x (0)2 + (-1) x (-1) + 1, =0+1+1=2, (iii) 2a2b + 2ab2 + ab, = 2 x (0)2 x (-1) + 2 x (0) x (-1) x (-1) + 0 x (-1), = 0 + 0 + 0 = 0 (iv), a2 + ab + 2, = (0)2 + 0 x (-1) + 2, =0+0+2=2, , Q6 :, Simplify the expressions and find the value if x is equal to 2, (i) x + 7 + 4 (x - 5) (ii) 3 (x + 2) + 5x - 7, (iii) 6x + 5 (x - 2) (iv) 4 (2x -1) + 3x + 11, Answer :, (i) x + 7 + 4 (x - 5) = x + 7 + 4x - 20, = x + 4x + 7 - 20, = 5x - 13
Page 19 :
Answer :, (i) z3 - 3 (z - 10) = z3 - 3z + 30, = (10 x 10 x 10) - (3 x 10) + 30, = 1000 - 30 + 30 = 1000, (ii) p2 - 2p - 100, = (-10) x (-10) - 2 (-10) - 100, = 100 + 20 - 100 = 20, , Q9 :, What should be the value of a if the value of 2x2 + x - a equals to 5, when x = 0?, Answer :, 2x2 + x - a = 5, when x = 0, (2 x 0) + 0 - a = 5, 0 - a = 5 a = -5, , Q10 :, Simplify the expression and find its value when a = 5 and b = -3. 2, (a2 + ab) + 3 - ab, , Answer :, 2 (a2 + ab) + 3 - ab = 2a2 + 2ab + 3 - ab, = 2a2 + 2ab - ab + 3, = 2a2 + ab + 3, = 2 x (5 x 5) + 5 x (-3) + 3, = 50 - 15 + 3 = 38, , << Previous Chapter 11 : Perimeter and AreaNext Chapter 13 : Exponents and Powers >>, , Exercise 12.4 : Solutions of Questions on Page Number : 246, Q1 :, Observe the patterns of digits made from line segments of equal length. You will find such segmented digits on the, display of electronic watches or calculators. (a), , (b), , (c)
Page 20 :
If the number of digits formed is taken to be n, the number of segments required to form n digits is given by the, algebraic expression appearing on the right of each pattern., How many segments are required to form 5, 10, 100 digits of the kind ,, , ,, , ., , Answer :, (a) It is given that the number of segments required to form n digits of the kind, is (5n + 1)., Number of segments required to form 5 digits = (5 x 5 + 1), = 25 + 1 = 26, Number of segments required to form 10 digits = (5 x 10 + 1), = 50 + 1 = 51, Number of segments required to form 100 digits = (5 x 100 + 1), = 500 + 1 = 501, (b) It is given that the number of segments required to form n digits of the kind, , is (3n + 1)., , Number of segments required to form 5 digits = (3 x 5 + 1), = 15 + 1 = 16, Number of segments required to form 10 digits = (3 x 10 + 1), = 30 + 1 = 31, Number of segments required to form 100 digits = (3 x 100 + 1), = 300 + 1 = 301, (c)It is given that the number of segments required to form n digits of the kind, Number of segments required to form 5 digits = (5 x 5 + 2), = 25 + 2 = 27, Number of segments required to form 10 digits = (5 x 10 + 2), = 50 + 2 = 52, Number of segments required to form 100 digits = (5 x 100 + 2), = 500 + 2 = 502, , is (5n + 2).
Page 21 :
Q2 :, Use the given algebraic expression to complete the table of number patterns. The, given table can be completed as follows.